基于ANSYS Workbench齒輪穩(wěn)態(tài)溫度場(chǎng)有限元分析

任敏強(qiáng),吳紹峰,段曉飛

(1.西南交通大學(xué) 機(jī)械學(xué)院，四川 成都 610000;2.北京工業(yè)大學(xué) 機(jī)械工程與應(yīng)用電子技術(shù)學(xué)院，北京 100000)

0 引言

齒輪是機(jī)車傳動(dòng)系統(tǒng)的核心部件，保證其運(yùn)行的安全可靠性是現(xiàn)代機(jī)械設(shè)計(jì)的重中之重。齒面膠合是傳動(dòng)系統(tǒng)的常見(jiàn)故障之一，也是造成輪齒破壞的重要原因。因?yàn)槟Σ潦軣崾沟谬X面溫度升高，溫度過(guò)高散熱不及時(shí)就會(huì)導(dǎo)致輪齒嚙合過(guò)程中產(chǎn)生膠合，影響齒輪的正常工作[1]。因此，分析齒輪達(dá)到穩(wěn)態(tài)溫度后輪齒的溫度場(chǎng)分布及熱變形情況就具有重要的工程運(yùn)用意義。

Fratila D和Radu A[2]在齒輪銑削加工過(guò)程中，提出使用有限元方法對(duì)齒輪加工的穩(wěn)態(tài)熱進(jìn)行仿真研究。Fan Zhimin等[3]利用ANSYS軟件對(duì)雙漸開(kāi)線齒輪傳動(dòng)進(jìn)行穩(wěn)態(tài)溫度場(chǎng)有限元分析，得到輪齒最大溫度值變化規(guī)律。徐宏海等[4]提出基于流場(chǎng)仿真分析及監(jiān)測(cè)數(shù)據(jù)來(lái)精確計(jì)算齒輪的對(duì)流換熱系數(shù)。鄧先智[5]通過(guò)超松弛迭代計(jì)算方法研究得到節(jié)點(diǎn)處的油膜溫度接近穩(wěn)態(tài)潤(rùn)滑油的溫度的結(jié)論。陳長(zhǎng)征等[6]利用ANSYS軟件研究風(fēng)力發(fā)電機(jī)單個(gè)輪齒的熱變形，分析了電機(jī)齒輪溫度隨功率和轉(zhuǎn)速的變化規(guī)律。臧立彬等[7]采用摩擦磨損試驗(yàn)機(jī)獲得涂層表面的摩擦因數(shù),運(yùn)用ANSYS軟件仿真揭示了涂層摩擦因數(shù)、轉(zhuǎn)速等與齒輪穩(wěn)態(tài)溫度場(chǎng)的關(guān)系。方特[8]和馬玉強(qiáng)等[9]通過(guò)對(duì)高速齒輪的潤(rùn)滑油特性的研究揭示了溫度對(duì)油黏度的影響。涂文兵等[10]通過(guò)有限元軟件分析齒輪嚙合過(guò)程中彎曲強(qiáng)度的變化，對(duì)齒輪的優(yōu)化設(shè)計(jì)提供了幫助。本文主要研究某重載機(jī)車齒輪箱達(dá)到穩(wěn)態(tài)后齒輪本體溫度場(chǎng)分布及熱變形情況，為提高齒輪強(qiáng)度和輪齒修形及優(yōu)化設(shè)計(jì)提供理論支持。

1 齒輪穩(wěn)態(tài)溫度場(chǎng)有限元分析流程

本文僅研究齒輪副的兩個(gè)嚙合簡(jiǎn)化單齒。首先利用三維建模軟件SolidWorks建立標(biāo)準(zhǔn)漸開(kāi)線齒輪模型并裝配，并通過(guò)軟件內(nèi)的分割功能將齒輪分割為單齒幾何模型。然后將模型導(dǎo)入ANSYS Workbench中進(jìn)行穩(wěn)態(tài)熱分析，將得到的溫度場(chǎng)作為體載荷加載到靜力學(xué)模塊中分析模型的熱變形。齒輪穩(wěn)態(tài)本體溫度場(chǎng)仿真流程如圖1所示。

圖1 齒輪穩(wěn)態(tài)本體溫度場(chǎng)仿真流程

2 有限元熱分析邊界條件計(jì)算

齒輪各個(gè)面邊界條件的正確計(jì)算是齒輪穩(wěn)態(tài)溫度場(chǎng)仿真的重要保障，所以必須確定齒輪各個(gè)面的熱量傳遞情況。本文將齒輪單齒的計(jì)算區(qū)域分為齒面嚙合區(qū)、齒頂和齒根及齒面非嚙合區(qū)、齒輪端面、齒輪分齒截面，如圖2所示。

(1) 齒面嚙合區(qū)(m區(qū))。該區(qū)域輪齒相對(duì)滑動(dòng)有摩擦熱生成，還與介質(zhì)有對(duì)流換熱，滿足第二類和第三類邊界條件：

(1)

其中：λ為導(dǎo)熱系數(shù)；αt/αn為等溫面法線方向的溫度梯度；hm為嚙合區(qū)對(duì)流換熱系數(shù)；t為輪齒邊界溫度；tm為嚙合區(qū)潤(rùn)滑油溫度；qm為嚙合面熱流密度。

齒面嚙合區(qū)(m區(qū))換熱系數(shù)為：

(2)

其中：Ref為潤(rùn)滑油雷諾數(shù)；Prf為潤(rùn)滑油普朗特?cái)?shù)；λf為潤(rùn)滑油熱傳導(dǎo)系數(shù)；dw為零件特征尺寸，齒輪一般取節(jié)圓直徑。

(2) 齒頂和齒根及齒面非嚙合區(qū)(f區(qū))。該區(qū)域存在對(duì)流換熱的邊界條件，屬于第三類邊界條件：

(3)

其中：hf為非嚙合區(qū)對(duì)流換熱系數(shù)；tf為非嚙合區(qū)潤(rùn)滑油溫度。

齒頂和齒根及齒面非嚙合區(qū)(f區(qū))換熱系數(shù)為：

(4)

(3) 齒輪端面(d區(qū))。該區(qū)域存在對(duì)流換熱的邊界條件，屬于第三類邊界條件：

(5)

其中：hd為齒輪端面對(duì)流換熱系數(shù)；td為齒輪端面潤(rùn)滑油溫度。

(4) 齒輪分齒截面(e區(qū))的熱分析邊界條件為：

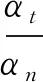
(6)

3 齒輪摩擦熱流密度計(jì)算

直齒輪嚙合軸向示意圖見(jiàn)圖3。根據(jù)圖3，嚙合點(diǎn)S與節(jié)點(diǎn)P的距離為：

(7)

其中：r1為主動(dòng)輪節(jié)圓半徑；R1為嚙合點(diǎn)到主動(dòng)輪中心的距離；α為齒輪壓力角。

設(shè)ω1、ω2分別為主、從動(dòng)輪角速度，則有：

(8)

其中：n為主動(dòng)輪的轉(zhuǎn)速；r2為從動(dòng)輪的節(jié)圓半徑。

圖2 單齒計(jì)算區(qū)域

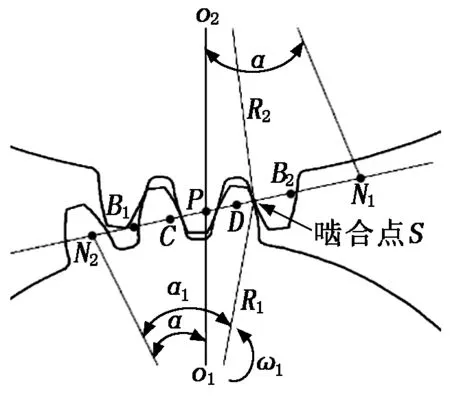
圖3 直齒輪嚙合軸向示意圖

主、從動(dòng)齒輪沿切線方向的絕對(duì)速度為：

(9)

(10)

主、從動(dòng)齒輪相對(duì)滑動(dòng)速度為：

(11)

根據(jù)公式運(yùn)用MATLAB編制程序繪制主、從動(dòng)輪齒面滑動(dòng)速度，如圖4所示。

本文研究某重載機(jī)車傳動(dòng)系統(tǒng)的漸開(kāi)線圓柱直齒齒輪，采用SolidWorks軟件建模并裝配，其建模基本參數(shù)如下：主動(dòng)齒輪齒數(shù)為23，從動(dòng)齒輪齒數(shù)為120；模數(shù)m=8 mm；壓力角為20°；大、小齒輪齒寬均為140 mm。

平均赫茲接觸應(yīng)力為：

(12)

其中：Fn為齒輪法向力；Rs1、Rs2為嚙合點(diǎn)齒面嚙合半徑；L為齒寬；μ1、μ1和E1、E2分別為主、從動(dòng)輪的泊松比和彈性模量。

嚙合線上任意點(diǎn)S在單位時(shí)間單位面積上的平均生熱量Qs為:

Qs=ε·f·σavg·v.

(13)

其中：ε為熱能轉(zhuǎn)換系數(shù)；f為摩擦因數(shù)。

齒輪嚙合引入熱分配系數(shù)?k。假設(shè)齒輪產(chǎn)生的滑動(dòng)摩擦熱Qs全部被主、從動(dòng)輪吸收，主動(dòng)輪吸收熱量為?kQs，則從動(dòng)輪吸收熱量為Qs(1-?k)。?k由下式計(jì)算：

(14)

其中：λ1、λ2分別為主、從動(dòng)齒輪材料的導(dǎo)熱系數(shù)；ρ1、ρ2分別為主、從動(dòng)齒輪材料的密度；c1、c2分別為主、從動(dòng)齒輪材料的比熱容。

主動(dòng)齒輪與從動(dòng)齒輪的平均生熱量為：

(15)

主、從動(dòng)輪的摩擦熱流密度為：

(16)

通過(guò)MATLAB編制程序繪制齒輪副的摩擦熱流密度曲線，如圖5所示。

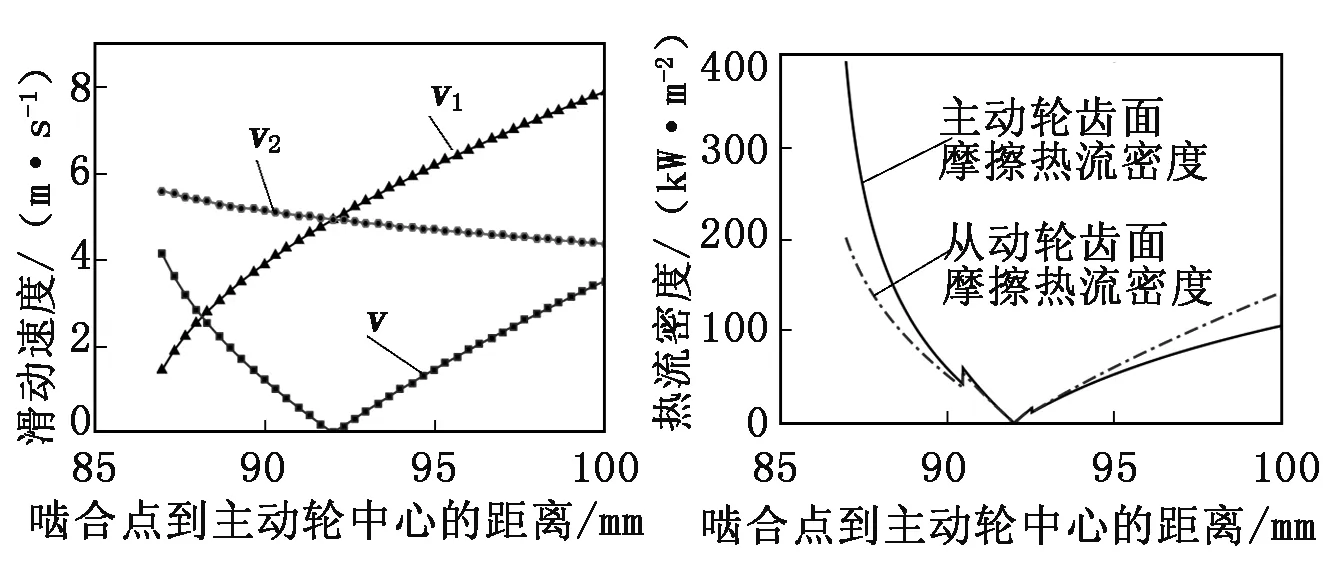
圖4 嚙合齒面滑動(dòng)速度 圖5 齒輪面摩擦熱流密度

4 齒輪穩(wěn)態(tài)溫度場(chǎng)有限元分析

4.1 輪齒網(wǎng)格劃分

Solid90是高階20節(jié)點(diǎn)的六面體單元，在單元各棱邊有個(gè)中間節(jié)點(diǎn)，Solid90六面體單元形狀還可以根據(jù)研究對(duì)象形狀自動(dòng)調(diào)整為棱柱體，更加貼近分析模型，所以本文穩(wěn)態(tài)溫度場(chǎng)仿真模型網(wǎng)格劃分采用Solid90單元。

主、從動(dòng)齒輪熱分析網(wǎng)格劃分如圖6所示。主動(dòng)輪的單元數(shù)為87 804、節(jié)點(diǎn)數(shù)為376 926；從動(dòng)輪的單元數(shù)為91 760、節(jié)點(diǎn)數(shù)為394 116；主、從動(dòng)齒輪的嚙合面采用局部網(wǎng)格加密，其他表面正常網(wǎng)格劃分。

4.2 輪齒穩(wěn)態(tài)溫度場(chǎng)仿真

運(yùn)用有限元軟件對(duì)齒輪單齒本體溫度場(chǎng)進(jìn)行仿真分析。首先將前面理論計(jì)算的熱流密度分別加載在齒輪的嚙合面，然后在齒輪的嚙合區(qū)、非嚙合區(qū)、端面、齒輪分齒截面分別加上對(duì)流換熱系數(shù)的邊界條件，用ANSYS Workbench進(jìn)行仿真計(jì)算，得到齒輪溫度場(chǎng)與熱變形云圖，如圖7所示。

由圖7(a)、7(b)可知：高溫區(qū)域主要分布在嚙合面的齒寬中部，且齒輪嚙入位置附近溫度相對(duì)最高；從動(dòng)輪的最高溫度低于主動(dòng)輪的最高溫度。由圖7(c)、7(d)可知：兩個(gè)單齒的變形趨勢(shì)一致；兩輪齒的兩端面角的熱變形量最大，主動(dòng)輪單齒本體最大熱變形為0.034 5 mm，從動(dòng)輪為0.032 5 mm。

圖6 齒輪熱分析網(wǎng)格劃分

圖7 齒輪溫度場(chǎng)及熱變形云圖(轉(zhuǎn)速n=1 500 r/min)

4.3 不同工況主動(dòng)輪單齒有限元分析

本文通過(guò)對(duì)不同轉(zhuǎn)速工況下的本體溫度場(chǎng)仿真，研究轉(zhuǎn)速對(duì)主動(dòng)輪本體溫度大小及分布的影響，仿真結(jié)果如圖8所示。

圖8 主動(dòng)輪不同轉(zhuǎn)速的溫度場(chǎng)

根據(jù)圖8可知：隨著主動(dòng)輪轉(zhuǎn)速由1 200 r/min、1 500 r/min、1 800 r/min逐漸增大，齒輪最高本體溫度分別為87 ℃、94 ℃、100 ℃也逐漸增加，且對(duì)應(yīng)的最低溫度也增加；齒輪不同轉(zhuǎn)速時(shí)嚙合面的最高溫度均出現(xiàn)在齒寬方向中間位置的齒根圓附近，最低溫度出現(xiàn)在齒輪兩端面遠(yuǎn)離嚙合面的位置。

5 結(jié)語(yǔ)

本文基于ANSYS Workbench對(duì)某重載機(jī)車齒輪穩(wěn)態(tài)溫度場(chǎng)進(jìn)行仿真分析，得出以下結(jié)論：

(1) 不同轉(zhuǎn)速下主動(dòng)齒輪與從動(dòng)齒輪溫度場(chǎng)分布相似，主動(dòng)輪最高溫度高于從動(dòng)輪，且最高溫度分布在齒寬中部的齒根圓附近。

(2) 主、從動(dòng)齒輪的熱變形場(chǎng)規(guī)律相同，輪齒兩側(cè)靠近齒頂處變形最大，相同工況時(shí)主動(dòng)輪變形量略大于從動(dòng)輪。

(3) 鑒于ANSYS Workbench有限元軟件的可視化操作界面，能更加準(zhǔn)確直觀地分析輪齒的溫度場(chǎng)，方便研究開(kāi)展輪齒的修形優(yōu)化工作。