如何用Scratch或Python判斷阿姆斯特朗數

在我們數學王國中，存在著很多有別稱的數字，今天我們來認識一位新朋友——“阿姆斯特朗數”。阿姆斯特朗數是數學中的一個概念，多用于計算機語言中，如果一個n位正整數等于其各位數字的n次方之和則稱該數為阿姆斯特朗數。 例如1^3 + 5^3 + 3^3 = 153。

已知1000以內的阿姆斯特朗數： 1， 2， 3， 4， 5， 6， 7， 8， 9， 153， 370， 371， 407。

那么大家肯定會想，我們如何來判斷阿姆斯特朗數呢？判斷的方法和依據又是什么呢？我們用Scratch來編寫一下判斷程序，輸入一個三位數判斷是不是阿姆斯特朗數。

由于僅僅是對三位數判斷，難度不高，先判斷輸入的數字是否為三位數，如果不是，停止所有腳本。

如果是三位數的話繼續判斷，判斷方法有兩種供你參考：

1.用到提取字符積木。從回答的結果中直接依次提取字符出來，個位是“‘回答的第一個字符”，十位提取第二個，百位提取第三個。這里我們首次用到了運算中的“…的第…個字符”積木。

2.運算法。假設輸入數為456，提取百位數字的方法就是456整除100，結果為4（需要向下取整）;提取個位數字的方法是456除以10的余數，結果為6;要提取十位數字需要動腦筋思考一下，要結合整除和取余數兩個方法，首先向下取整456除10，結果為45，然后取除以10的余數得到5，就是十位的結果，數學運算的方法比較巧妙。

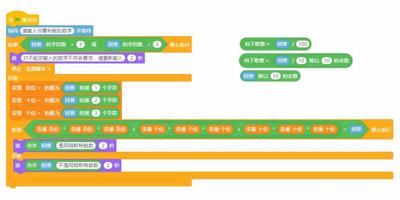
兩種方法均可選擇。

然后進行阿姆斯特朗數的判斷，個位的三次方+十位的三次方+百位的三次方之和是否等于該數字本身。

Scratch代碼通俗易懂，下面進行一次小小的提升嘗試，用Python來編寫，輸入一個數字（不考慮數字的位數）來進行判斷是否為阿姆斯特朗數。

這里我們用到while循環，當while=0時結束循環，提取的方法是剛才用到的運算法，從個位開始每次取除10的余數，提取出最后一位數字，然后依次往前高位提取，不要忘記每次的循環結束前除以10并向下取整，否則每次提取的數字都是一樣的，循環結束后，進行比較判斷是否為阿姆斯特朗數，代碼如下：

本題的關鍵就是把輸入數字作為字符串用提取法處理，還是當作數字用整除取余數的運算法處理。