用表面張力實驗簡單分析氣體模型

葛 素 紅 馬 喜平 孫桂 華，2 王 新星，2

（1.河西學院物理與機電工程學院；2.河西學院物理與機電工程學院理論物理研究所，甘肅 張掖 734000）

1 引言

熱力學的一個主要任務是研究熱力學系統在所發生的與熱現象有關的過程中所體現的物質性質和規律.最簡潔和有效的方法，就是確定物質體系的物態方程.人們獲得物態方程有效的辦法是實驗地總結和驗證，這就使得良好物態方程的獲得在實際中很困難，到目前為止，理論上得到的最好、最精確的物態方程就是理想氣體狀態方程，它可以用來處理各種過程中氣體物性的分析研究，但在實際的生產和生活之中，是不存在理想氣體的，實際中人們所接觸到的，都是實際氣體.而且，人們所呼吸的空氣，不只是實際氣體，它是實際氣體的混合物.

1662年英國科學家玻意耳、1679年法國科學家馬略特分別對給定量的稀薄氣體在等溫過程中的性質進行了實驗研究，得到了稀薄氣體的等溫定律［1］.1802～1809年法國化學家、物理學家蓋·呂薩克發現了稀薄氣體的熱膨脹定律，而在此之前的1746～1823 年間法國物理學家查理就發現了稀薄氣體在體積不變的條件下，其壓強隨溫度的變化作線性改變的實驗規律［2，3］.這就是著名的氣體實驗三定律，經過人們在實驗和理論上的分析認為，壓強很小的稀薄氣體，其宏觀性質與氣體種類沒有關系，因此，把滿足實驗三定律的氣體稱為理想氣體.到1834年法國物理學家和土木工程師克拉珀龍將氣體實驗定律歸納為理想氣體狀態方程.若氣體系統平衡態參量為P、V、T，系統物質的量為n，R為普適氣體常量，則其狀態方程表示為［1］：

1801年英國化學家、物理學家道爾頓提出了混合氣體分壓定律，為我們研究空氣的性質提出了可貴的理論依據.他認為同溫度同體積的條件下，混合氣體的壓強等于相同條件下各種氣體分壓強的求和［1］：

當把氣體看成理想氣體，就意味著忽略了氣體的個性，從微觀上來分析，就意味著所有種類氣體分子的大小都被忽略了，同時，也忽略了氣體分子之間還應該存在的相互吸引的作用力.1873年荷蘭物理學家范德瓦耳斯根據這兩點提出修正，給出了一種實際氣體狀態方程［1］：

其中a和b分別是氣體分子體積和分子間吸引力的修正參數，它們與氣體種類有關，不同氣體分子的這兩個參數是不相同的，一般地這兩個參數由相關實驗來確定.

1901年在研究永久性氣體的液化時，荷蘭物理學家昂內斯將稀薄氣體以體積展開，給出了另一種實際氣體狀態方程［4］：

如果只考慮二級修正，方程式如下：

其中B是第二位力系數，斥力對其貢獻為正，引力對其貢獻為負.比較（4）和（5）式可以認為范德瓦耳斯方程是展開到二級近似的昂內斯方程，由此可以認為，對于壓強不太大的氣體，溫度較高情況下，分子間引力對氣體的性質影響很小，這時主要是分子發生碰撞時的斥力起主要作用.而當溫度較低時，情況則剛好相反.通常情況下，在300K左右，第二位力系數為負，說明分子間引力對氣體性質的影響較斥力更加重要.這從另一個側面說明了范德瓦耳斯方程只考慮分子間引力修正具有一定的正確性和適用性.

由于范德瓦耳斯方程是對實際氣體的逼近，其氣體參數的獲得主要依賴于氣液相變過程中臨界點狀態參數的測量.因此，到目前為止單獨的關于范德瓦耳斯氣體參數的研究文獻未見報道.而在液體的表面張力現象的研究中有一個結論，我們可以通過測量球形肥皂泡的液體表面張力系數σ 和肥皂泡的半徑r來計算球形肥皂泡內外的壓強差［1］：

其中σ 是液體的表面張力系數，r是肥皂泡的半徑.肥皂泡內外都是混合氣體.基于（6）式本文設計實驗測量了肥皂泡的表面張力系數和半徑，計算獲得其內外壓強差，這個差值與肥皂泡內外氣體特性有關，可以此來推算肥皂泡內外氣體的特性.

2 實驗結果與討論

2.1 實驗原理和用具

在液體與氣體交界面處液體表面存在著一個薄層，這個薄層通常稱作液體的表面層.由于物質的微觀結構在這個薄層處與氣體內部和液體內部的情況都不相同，在這個薄層處就表現出一種特殊的表面現象，即表面張力現象.這種特殊的現象使自然界更加色彩繽紛了，出現了很多有意思的景觀，五顏六色的肥皂泡泡就是表面現象的一種.而泡泡正是由于液體的表面張力而形成的.經過實驗驗證液體的表面張力等于表面張力系數與周界長度的乘積，因此，在給定的實驗條件下，表面張力系數σ 就表示其單位長度上的表面張力.

本實驗應用力敏傳感器比較全面地測量不同液體的表面張力系數.實驗主要裝置是FD-NST-I型液體表面張力系數測定儀.它的主要結構原理是量程范圍較小、靈敏度高且穩定性較好的硅壓力敏傳感器張力測定儀，測量液體的表面張力.將圓環狀金屬片吊掛在靈敏的測力計上，然后把它浸入到待測液體中，當緩緩移動高低位置時金屬圓環就會拉出一層與液體相連的液膜，由于表面張力的作用，與金屬環相連的力敏傳感器張力測定儀就會顯示出液膜拉斷前一瞬間數字電壓表讀數U1和液膜拉斷后一瞬間數字電壓表讀數U2.由于液膜有兩個表面，在一級近似條件下，可以認為脫離力為表面張力系數乘上脫離表面的周長，即［5-7］：

D1和D2分別為圓環的內徑和外徑. σ 為液體的表面張力系數.

硅壓力敏傳感器由彈性梁和貼在梁上的傳感器芯片組成，其中芯片由四個硅擴散電阻集成一個非平衡電橋，當外界壓力作用于金屬梁時，在壓力作用下，電橋失去平衡，此時將有電壓信號輸出，輸出電壓大小與外力成正比，即

式中，F 為外力的大小， K 為硅壓力敏傳感器的靈敏度，ΔU 為傳感器輸出的電壓差值大小.把（3）式和（4）時代入（2）式，即有：

對力敏傳感器張力測定儀定標之后就可以用作圖求斜率的方法求出靈敏度K 值，所以，只要測定液膜拉斷前一瞬間U1值和拉斷一瞬間值U2，計算出差值，即能得出液體表面張力系數σ 值.本實驗在同一實驗室用同一臺儀器，首先定標得到儀器的靈敏度K值為3.616mv/N.

2.2 市售泡泡液中加入不同物質組成混合溶液的表面張力系數及其吹出泡泡半徑的測定

表1 市售泡泡液中加入食鹽組成不同濃度的混合溶液的表面張力系數Tab.1 surface tension coefficients of bubble liquid of salt

在給定溫度條件下，測量不同濃度混合溶液的表面張力系數，獲得可以吹出泡泡的不同表面張力系數的溶液和其對應的表面張力系數，數據在表1和表2中列出.溶液的配制是以食鹽（中鹽甘肅省鹽業集團有限公司售）和白糖（市售散裝）為溶質，以市售的一種泡泡液（型號：MG952，汕頭市澄海區金鈿玩具有限公司產）為溶劑，按照質量百分比配制50g不同濃度的混合溶液，根據定義式：

稱量相應質量的食鹽、白糖后，與相應質量的泡泡液混合后，將食鹽和白糖分別加入到盛有泡泡液的燒杯中并用玻璃棒充分進行攪拌，待食鹽和白糖完全融化后靜置即可得到相應濃度的溶液.

表2 市售泡泡液中加入白糖組成不同濃度的混合溶液的表面張力系數Tab.2 surface tension coefficients of bubble liquid of sugar

市售泡泡液吹出的泡泡在空氣中飛翔，由于其自身重力的影響，實際上不會是標準的球形，但可以粗略地看作是一個球體.由于吹出的泡泡不易固定而且極其容易破裂，因此對于其半徑的測量，存在很大困難.2016年姜仲篪等人在研究泡泡大小與張力系數時用拍照對比方格紙的方法粗略測得了吹出泡泡的直徑，這種方法較為簡單且容易操作，但須兩個人來完成［8］.本實驗中設計了一種簡單易行的測量方法，是用吸管在光滑平整的桌面上吹出半個泡泡并直接測量了泡泡的半徑.為了使得所吹出的泡泡達到最大狀態，在吹泡泡之前，先用泡泡液將桌面潤濕，增大泡泡表面與桌面的潤滑程度.同時為了方便測量泡泡的高度，需將刻度尺豎直固定在桌面上，然后用吸管蘸取少量泡泡液，在濕潤的桌面上吹出半個泡泡，同時目光平視泡泡凸起面所對應的刻度尺上的高度，當泡泡炸裂的瞬間，讀出該時刻泡泡凸起面所對應的刻度即為該濃度（表面張力系數）下所吹出的最大泡泡的半徑，為了減小誤差需要多測量求取平均值，本次實驗在每一濃度下測量五次.

測量所得同濃度的食鹽混合溶液和白糖混合溶液的所吹出泡泡的半徑和對應的表面張力系數在表3和表4中列出.根據研究，液體溫度對液體表面張力有很大的影響［9-11］，而我們的實驗沒有能力統一測量時的環境溫度，因此，需要對表3和表4中所測量的表面張力系數數值進行修正.人們對純水表面張力系數研究比較廣泛，依據純水在0℃～100℃之間的表面張力系數測量值，擬合獲得了其表面張力系數隨溫度變化的經驗函數［12］，不同溫度下純水的表面張力系數如表5所示.但從物質的熱學形態上考慮，當溫度遠低于常溫時，水的凝聚態更強，而當溫度達到35℃以上時，表面蒸發現象也很明顯.本文實驗是在常溫下做的，上下溫差不超過5℃，因此，選15℃～30℃為最佳溫度段，擬合得到純水的表面張力系數隨溫度升高而降低的一級近似梯度為：0.155×10-3（N/m）.以此為溫度修正因子修正不同溫度下混合溶液的表面張力系數，并在表3和表4中第二行列出（以21℃為基準）.

表3 市售泡泡液中加入食鹽組成不同濃度的混合溶液吹出的泡泡半徑Tab.3 The bubble radius of the bubble liquid of salt

表4 市售泡泡液中加入白糖組成不同濃度的混合溶液吹出的泡泡半徑Tab.4 The bubble radius of the bubble liquid of sugar

表5 各溫度下水的表面張力系數的公認值Tab.5 surface tension coefficients of water

2.3 泡泡內外壓強差及空氣的模型分析

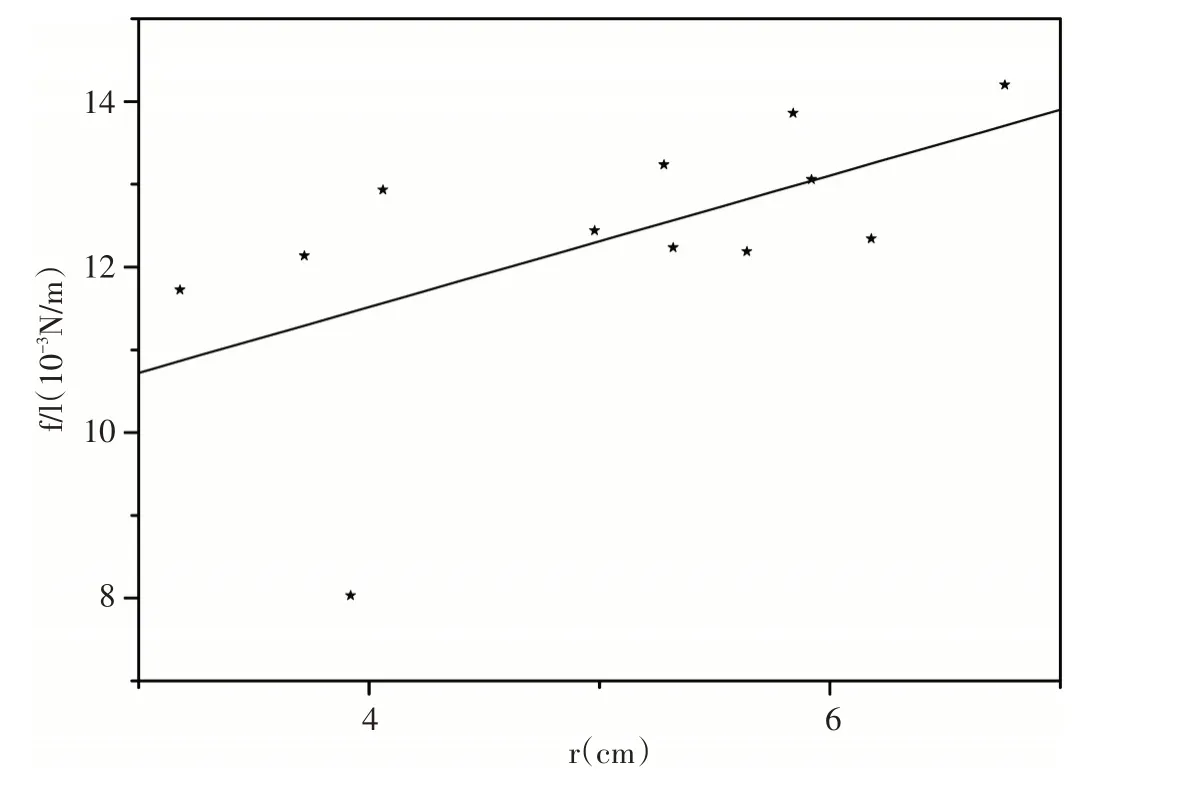
圖1 市售泡泡液中加入食鹽組成不同濃度的混合溶液的表面張力系數與其泡泡半徑相關曲線Fig.1 The relation between bubble radius and surface tension coefficient of Salt solution

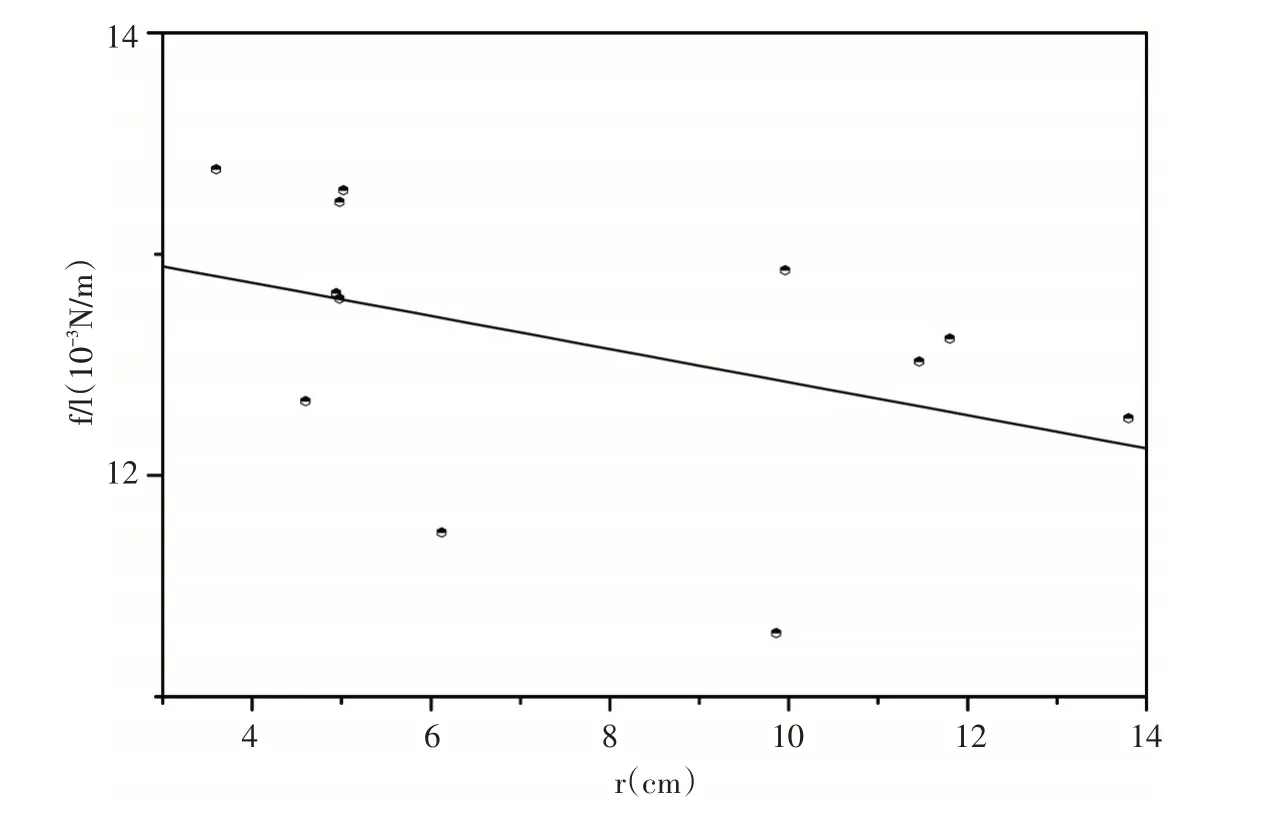
圖2 市售泡泡液中加入白糖組成不同濃度的混合溶液的表面張力系數與其泡泡半徑相關曲線Fig.2 The relation between bubble radius and surface tension coefficient of sugar solution

表3和表4中列出的測量所得同濃度的食鹽混合溶液和白糖混合溶液的所吹出泡泡的半徑和對應的表面張力系數的修正值，繪制表面張力系數σ 與泡泡半徑r的相關曲線如圖1和圖2所示.根據擬合結果，圖1 給出的斜率值為0.79444，而圖2 給出的斜率值為0.0748.依據公式（6）.按照圖1所顯示的，我們可以認為球形肥皂泡內外壓強差的實驗值為：

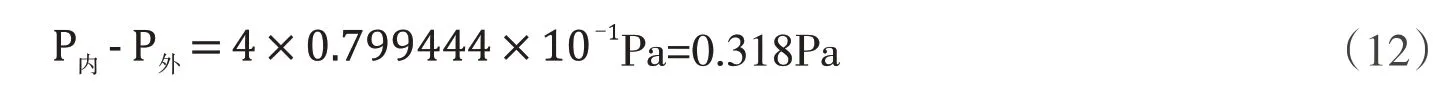
按照圖2所顯示的，我們可以認為球形肥皂泡內外壓強差的實驗值為：0.029Pa.

張掖市甘州區的大氣壓強，就是肥皂泡所處環境的外部壓強.它的數據的獲得有兩種方法，第一是調查張掖氣象數據，可知其年平均氣壓是852.0hPa.第二是根據等溫氣壓公式來計算其數據［1］：

式中p（0）是零海拔的氣壓，即為一個大氣壓，M 是空氣的摩爾質量，其數值為29；T 為空氣的溫度，本文設置為21℃（即所有的液體表面張力系數經過修正后表達為21℃的結果）；Z為張掖市甘州區的海拔，其數值為1467m.重力加速度g取張掖地區的數值為9.7807m/s2［13］.將數據代入（12）式，可計算得到張掖市甘州區的大氣壓強理論數據為：85190Pa，與氣象數據相差不大.

肥皂泡內的氣壓也可以有兩種算法，第一是當作理想氣體處理，則其內部氣壓可以根據（14）式建模計算.肥皂泡內部是人體吹出的氣體，將其看作理想氣體，并認為經過呼吸道的降溫作用，其溫度與環境溫度相同為21℃.人體呼出的氣體主要為氮氣（占78%）、氧氣（占16%）和二氧化碳（占6），其密度按比例計算為1.32kg/m3，摩爾質量為30g/mol.計算的氣泡內壓為106859Pa，大于一個標準大氣壓.

由（13）式和（14）計算所得球形肥皂泡內外壓強差很大，為21.669kPa，與實驗測量的結果相差四個數量級，這顯然是不合理的.雖然實驗測量有誤差，但在一定程度上反映了客觀事實，因此，本文認為，將環境大氣和球形肥皂泡內的氣體當成理想氣體模型來處理是不符合實際的.

用實際氣體模型來處理，則是利用（3）式范德瓦耳斯方程，對于單位摩爾數的實際氣體，（3）式可改寫為：

若將肥皂泡內外的氣體都看作是稀薄的（只考慮分子間吸引力）的氣體，它們由于氣體分子體積所產生的修正參數b基本上是相同的，因此，引起內外壓強差的主要部分是由壓強參數引起的，可以根據（15）式，對單位體積的氣體，獲得一個計算肥皂泡內外壓強差的簡易公式：

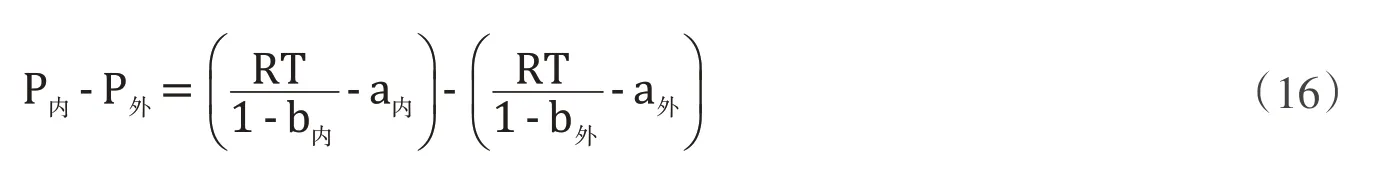
泡內氣體為人體呼出的氣體，泡外氣體為張掖地區的空氣，空氣的組成主要為氮氣（占78%）、氧氣（占21%）、氬氣（稀有氣體主要是氬氣，就當成氬氣處理，占0.94%）、二氧化碳（占0.03%）和水蒸氣（占0.03%）.取1mol單位體積的氣體，由于體積參數的影響幾乎可以忽略，只考慮壓強參數的影響.各種氣體的范德瓦耳斯壓強參數a和體積參數b在表6種列出，根據表6參數和氣泡內外氣體的組成比例計算可得氣泡內外壓強差為：0.0133Pa.與實驗測量的結果0.318Pa 和0.029Pa 相比較，這個數值只相差一個數量級，比較接近.因此，可以認為，無論是張掖地區的大氣，還是人體呼出的氣體，其實際模型都更接近范德瓦耳斯氣體，距離理想氣體這個簡化模型很遠.

圖6 氣體的范德瓦耳斯參數Fig.6 Van der Waals parameters of gas

3 結論

本文實驗測量了將食鹽和白糖加入市售泡泡液之中配制成的不同濃度的泡泡液的表面張力系數的大小，以及用不同的表面張力系數值的泡泡液吹出的泡泡的半徑.根據熱力學理論，球形肥皂泡的表面張力系數與其泡泡半徑的比值與球形肥皂泡內外壓強差成正比.在將球形肥皂泡內外氣體看成穩定氣體的情況下，可以用這個比值來推算球形肥皂泡內外壓強差.經過實驗和理論分析，本文發現：

1）在市售泡泡液里加入食鹽和白糖，隨著溶質的濃度的增大，泡泡液的表面張力系數呈下降的趨勢.

2）泡泡液的表面張力系數小于11×10-3N/m時，吹出泡泡的半徑已經比較小，即這個數值是良好泡泡液的一個臨界值.本實驗中市售泡泡液的表面張力系數的測量值是14.169×10-3N/m，可以認為這個數值是泡泡液表面張力系數的最佳值.

3）由于目前測量泡泡液的表面張力系數和泡泡液的半徑均存在較大的系統誤差，本文僅能給出定性的一個結果.根據本文實驗測得泡泡液表面張力系數與其半徑的比值計算可得泡泡液內外壓強差的數值約為0.318Pa或0.029Pa，即肥皂泡內外壓強差的數值范圍0.1～0.01Pa，是一個很小的值域.這也說明，肥皂泡的平衡是非常容易被破壞的.

4）若把肥皂泡內外的氣體看成理想氣體，用理想氣體模型理論計算肥皂泡內外壓強差，其數值為21.669kPa.與實驗數值相差6到7個數量級，顯然，把肥皂泡內外的氣體看成理想氣體是不合理的.

5）若把肥皂泡內外的氣體看成實際氣體，用范德瓦耳斯氣體模型理論計算肥皂泡內外壓強差，其數值為0.0133Pa，是在實驗數值的范圍內.因此，本文認為，在張掖這個海撥1400m 的地區，用范德瓦耳斯氣體模型來處理實際氣體，是合理和可行的.