數學學習的“破”與“立”
——蘇教版四下《認識三角形》教學實錄與思考

左 雷

學習蘇教版四下《認識三角形》之前，學生在生活中都接觸過一些表面呈三角形的物體，大多數學生都知道三角形有三個頂點、三條邊、三個角，知道三角形有高矮，能畫出三角形。因此，本節課的教學重點，是利用學生的原有認知，把學生對三角形外形的感性認識抽象成理性概念；引導學生理性認識三角形的高，并將三角形的高從生活中高矮的概念里剝離出來，感受生活物體的高矮與三角形的高的異同點；引導學生學會畫高。更重要的是，通過觀察、操作、比較等具體的活動，培養學生初步的分析、抽象、概括等能力，為今后繼續學習和探索多邊形的相關知識打下良好的基礎。基于上述認識，筆者以移動的磁點為載體，以磁點的位置變化為主線，以“先破后立”為立足點，引出數學問題，引發學生進行數學思考，促進他們開展深度學習。

一、認識三角形

1.基于經驗，畫三角形。

師（用三個磁點在黑板上擺出三角形）：看著這三個點，你能想象出什么平面圖形？（三角形）試著在空中比劃一下你看到的三角形。今天這節課，我們就來認識三角形。（板書課題）

師：給你這樣三個點，你能畫出一個三角形嗎？（學生在學習單上嘗試畫三角形）

引導學生從抽象的三個點想象三角形入手，再現已經形成的三角形表象，然后讓他們動手畫出具象的三角形，將頭腦中三角形的表象外顯出來，為下面認識三角形的特征做鋪墊。

2.基于活動，認識三角形的特征。

師（展示學生畫的兩幅三角形作品）：觀察這兩幅作品，結合剛才畫三角形的經驗，想一想，畫三角形時要注意什么？

生1：要畫直的。（板書：直的）

生2：要把這三個點連起來。（板書：連起來）

生3：畫的時候不能超過那個點。

師：你的意思是不能“過了”（用手比劃），對嗎？（板書：不能過了）如果請你介紹這個三角形，你準備怎么介紹？

生3：三角形有三個頂點、三個角、三條邊。

引導學生通過觀察、操作、比較進一步認識三角形的基本特征，積累認識圖形的經驗，為接下來抽象三角形的概念做準備。

3.基于積累，建構三角形的概念。

師：說到三角形的三條邊，老師突然想到一個問題。（動畫演示將三角形三條邊分開）你們看，三角形的每條邊各有兩個端點，三條邊就有六個端點，為什么三角形只有三個頂點呢？請把你的想法記在學習單上，記好后再跟同桌交流。

教師巡視，收集作品，然后多媒體展示學生作品。有的寫道：有頂點重合了，所以只能看到三個；有的寫道：因為有一些頂點重復了；有的寫道：有三個端點重疊了。

師：幾位同學表述不同，有相通的地方嗎？

生：“重合”“重復”“重疊”意思差不多。

師：“重合”是什么意思？誰跟誰重合了？

生：重合就是兩個點合在一起了，這條線段的一個端點和另一條線段的一個端點重合了。

師：如果咱們把端點排排序，（做手勢）從這開始到這結束，另一條又從這開始往這結束，開始的這個點叫“首”的話，那結束的這個點就叫？（尾）這樣的情況就叫？（首尾相接）（板書：由三條線段首尾相接圍成的圖形叫三角形）

師：回顧剛才大家畫三角形時提出的注意點，概念中有沒有指出三角形的邊是“直的”？

生：有，“線段”就是直的。

師：有沒有強調“連起來”呢？（首尾相接）哪個詞說的是不能“過了”？（圍成）

通過將三角形拆解成三條線段，由線段端點數量與三角形頂點數量不一致引發學生的認知沖突，從而激發他們自主建構“首尾相接”的概念。同時，通過與之前畫三角形時總結的注意點相比較，使學生深刻理解概念的內涵，達到“破”感性、“立”理性的教學目標。

4.基于練習，強化概念。讓學生在正例與反例辨析的過程中進一步明晰三角形概念的內涵與外延，掌握三角形的基本特征。

5.基于操作，理解頂點間的位置關系。

師：繼續觀察這三個磁點，如果把這個點擺在這兒（向上或向下移動最上面的頂點，保證三點不在一條直線上），現在還能看出這是三角形嗎？（能）現在呢？（可以）擺在這兒呢？（可以）

師：看來這個點很自由。像這樣移動下去，可以擺出多少個不同的三角形呢？

生（思考后）：無數個。

師：那擺在這兒行嗎？（移動磁點，讓三個點在一條直線上）（不行）擺在這兒呢？（也不行）

師：這個點好像也沒那么自由，它到底放哪兒行，放哪兒不行呢？

生：三個點不能擺在一條直線上。

師：為什么三個點不能擺在一條直線上呢？

生1：三角形得有三個角，這樣擺就沒有三個角了。

生2：如果三個頂點擺在一條直線上，連接三個點就沒有高度了，只能畫出一條直線。

教師繼續運用可移動的磁點來代替三角形的三個頂點，并引導學生在移動磁點的過程中感受三角形三個頂點的“自由”和“約束”，體會“無限”和“受限”，從而“破”表象、“立”本質。

二、認識三角形的高

1.感知三角形的高矮。

師（指著三個磁點）：回到剛才這個三角形，記住它的樣子。（不斷向上移動上面的磁點）這個三角形跟剛才比，有什么變化？（變高了）現在呢？（又變高了，繼而向下移動這個磁點）現在呢？（變矮了）看來三角形也是有高矮的。

2.研究三角形的高。

（1）比高矮。課件出示下頁圖1。

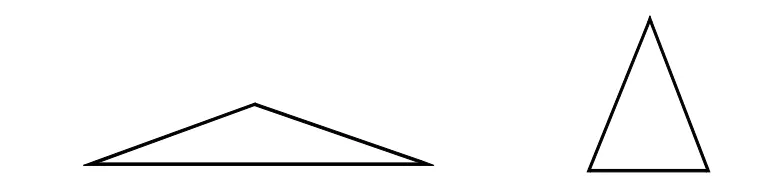
（圖1）

師：你覺得這兩個三角形，哪個高？

生：第二個三角形高。

師：怎么證明？兩個三角形究竟有多高？

學生自主畫高，教師巡視，然后展示如圖2所示的作品1～3。

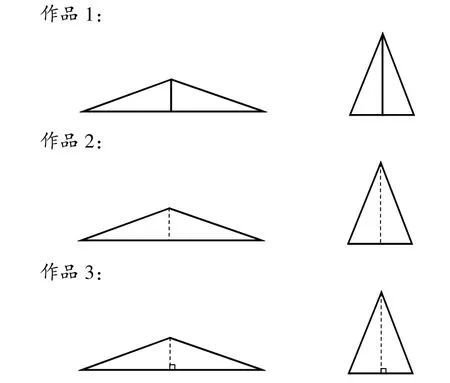
（圖2）

師：你們覺得哪個作品表達得更準確？

生1：首先可以排除作品1，因為實線就表示將這個三角形分成兩部分了，這里用虛線更合適，虛線表示這條線是后畫的。

生2：作品3 更準確，他畫的是虛線，而且標了直角標記，說明畫的是垂線。

師：都是虛線，為什么畫垂線更準確呢？

…………

師：是的，三角形的高就是從頂點到對邊的垂直線段。

（2）教學畫高。教師演示畫高，強調注意點。

（3）練習畫高。學生獨立完成練習，教師找生成并有序展示如圖3 所示的作品1～3。

師：觀察這三個作品，大家有什么想說的？

生1：作品1 第三個三角形的高畫錯了，應該從頂點向對邊畫垂直線段。

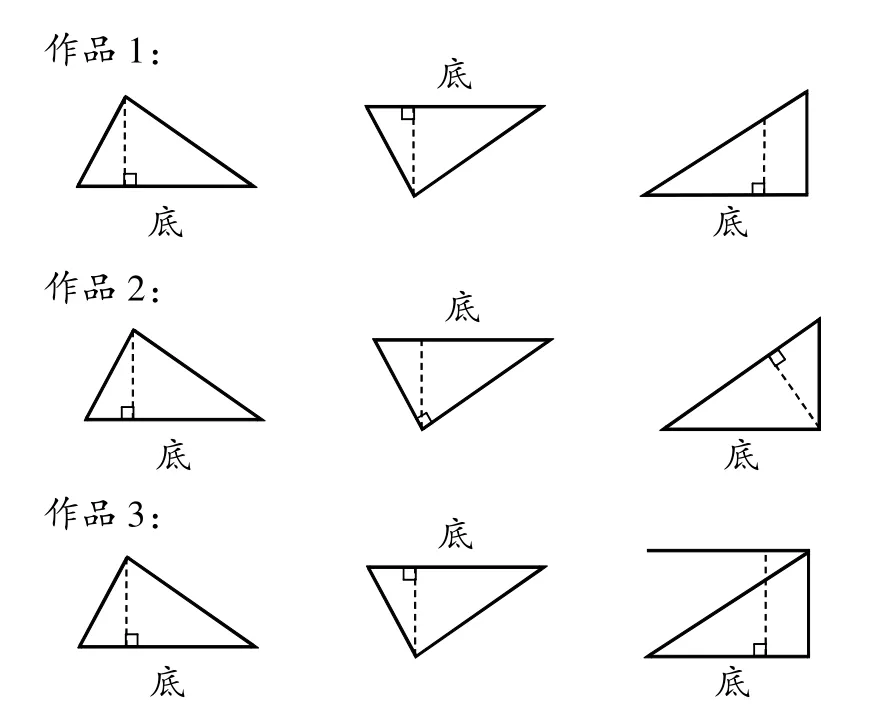
（圖3）

生2：作品2 第二個高的垂直標記標錯了，應該標在底上，因為這是表示與底垂直的線段。

生3：作品2 第三個三角形的高畫錯了。他畫的是斜邊上的高。

師：看來三角形的高和底是有講究的，它們是“對應”的。作品3 第三個圖形中畫的是高嗎？

生：不是，這條線段不是從頂點到對邊的垂直線段。

師：這條線段與高有什么關系呢？

生：因為平行線間的垂直線段的長度都相等，所以這條線段的長度和三角形的高相等。

師：三角形的高與生活中的高矮一樣嗎？

生：不一樣，高矮只是指長度，三角形的高是頂點到對邊的垂直線段。

師：聽明白了嗎？看來，三角形的高不只包含長度。大家對三角形高的感覺越來越好了！

借助學生“比高矮”的生活經驗，幫助他們初步建立三角形高的概念；接著，讓學生在對比中感知生活中的高矮與三角形的高的差異；進而將三角形的高從生活中高矮的概念中剝離出來，達到“破”經驗認知、“立”概念實質的目的。

很多時候，學習就是學生不斷打破原有認知，逐步重建新的認知的過程。