堤(壩)基層狀粗粒土發生滲透變形的顆粒運移規律

黃海均,嚴新軍*,毛海濤,王正成

(1.新疆農業大學水利與土木工程學院，烏魯木齊 830052；2.河北工程大學水利水電學院，邯鄲 056002；3.重慶三峽學院土木工程學院，萬州 404100)

堤(壩)基中常出現互層的粗粒土透水層，是滲透薄弱區域，極易發生滲透破壞，具有代表性的粗粒土互層主要由砂礫石層、細砂層和砂礫石層組成，滲透時各土層微觀的顆粒運移規律對于揭示堤(壩)基滲透變形和破壞機理至關重要[1]。因此，需要深入研究層狀粗粒土滲透變形顆粒運移規律。

近年來，中外學者針對管涌發生機理開展了大量的研究工作。劉昌軍等[2]、梁越等[3]利用室內砂槽模型試驗對單、雙層堤(壩)基管涌的發生及發展過程進行了模擬，將管涌破壞的發生及發展過程劃分為4個階段；賈愷等[4]利用自行設計試驗裝置對雙層堤(壩)基管涌通道擴展機制進行試驗，得出了雙層堤(壩)基管涌通道是否擴展取決于通道內沖刷水流、邊壁滲流力和砂層顆粒條件等因素。Shamy等[5]運用顆粒流方法，對上游水位上升時層狀堤(壩)基發生管涌導致水工建筑物出現較大位移和沉降的過程進行了模擬；文獻[6-7]給出了單一砂層堤(壩)基上臨界水頭的理論解答。不難發現，目前中外對此類問題的研究主要集中于管涌臨界滲透破壞條件的判別和單雙層堤(壩)基管涌通道發展機理方向，而對此類堤(壩)基管涌發展過程中顆粒運移特點研究極少，因此很有必要對層狀覆蓋層開展相關研究。

針對典型堤(壩)基的層狀粗粒土進行研究，利用顆粒流軟件PFC3D建立對應數值模型，模擬堤(壩)基顆粒運移特點及滲透變形發展過程并分析顆粒流失量、下沉量等參數的變化，為進一步認識層狀覆蓋層堤(壩)基滲透破壞提供參考。

1 顆粒流程序計算原理

1.1 流體相方程

在固液兩相體系中，相對于固體顆粒間孔隙體積變形量，液體的體積變形量幾乎可以忽略不計，因此可將顆粒孔隙中的流體視為密度不變的不可壓縮流體，在求解滲流場的每一時步中，滿足流體運動的連續性方程和平均Navier-Stokes[8]方程：

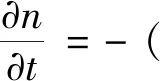
(1)

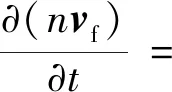
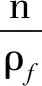
(2)

式中，n為顆粒孔隙率；t為時間；為拉普拉斯算子，為流體的速度矢量；ρf為流體密度；p為壓力梯度；τ為流體黏性應力張量；g為重力加速度矢量；fint為單位體積內顆粒與流體的相互作用力矢量。

1.2 固體相方程

對于固體顆粒，考慮流體作用時，其主要受到流體對顆粒、顆粒間相互作用及外應力等作用力，并通過牛頓第二定律來實現模擬顆粒的運動，此時顆粒運動方程為

(3)

(4)

式中，mp為顆粒的質量；vp為顆粒速度矢量；fg為重力加速度矢量；fc為接觸c(c=1，2，…，n)處顆粒間的接觸力；fd為顆粒在流體作用下受到拖曳力，包含浮力及固液之間的相互作用力；Ip為顆粒的轉動慣量；wp為顆粒的轉動速度矢量；rc為顆粒間接觸處指向顆粒中心的方向矢量。

1.3 流固耦合方程

固體顆粒在單個流體網格內的流動情況如圖1所示。

圖1 流體單元滲流示意圖Fig.1 Seepage diagram of fluid unit

流體單元網格體積為ΔV=ΔxΔyΔz，假定流體單元網格內包含np個顆粒，則流體單元網格內的孔隙率

(5)

式(5)中，dpi(i=1，2，…，n)為顆粒粒徑。

考慮流體單元網格內土體顆粒的受力平衡條件，可得單個固體顆粒受到的作用力

(6)

式(6)中，fdij為單個顆粒所受作用力分量；pj為流體壓力梯度分量。

對于穩定無分叉流，假設顆粒流體間的相互作用力只來源于壓力梯度，即：

fintj=npj

(7)

將式(7)代入式(6)，可得單個固體顆粒受到作用力的一般表達式：

(8)

當雷諾數為1～10的層流時，German將水力半徑理論公式代入Darcy公式得壓力梯度方程為

(9)

對于雷諾數大于10的紊流，Ergun[9]基于水力半徑理論提出了Ergun公式：

(10)

1.4 流固耦合過程

在顆粒流程序中，整個流體區域被劃分為若干個固定大小的流體計算單元，采用基于半隱式算法(SIMPLE法)結構的計算流體動力學(CFD)計算技術對液相流動方程進行求解。在計算過程中，首先根據力-位移定理計算得到顆粒間的接觸力，而后將該力與流體對顆粒的拖曳力一起代入下一時步顆粒運動方程中，以此確定顆粒新的位置、速度及接觸力等。同時顆粒的運動又將引起流體單元內壓力、流速、孔隙率的變化，進而影響到顆粒間接觸力及流體對顆粒拖曳力的變化，可見流固耦合模擬過程為一個動態循環平衡過程，其計算過程如圖2所示。

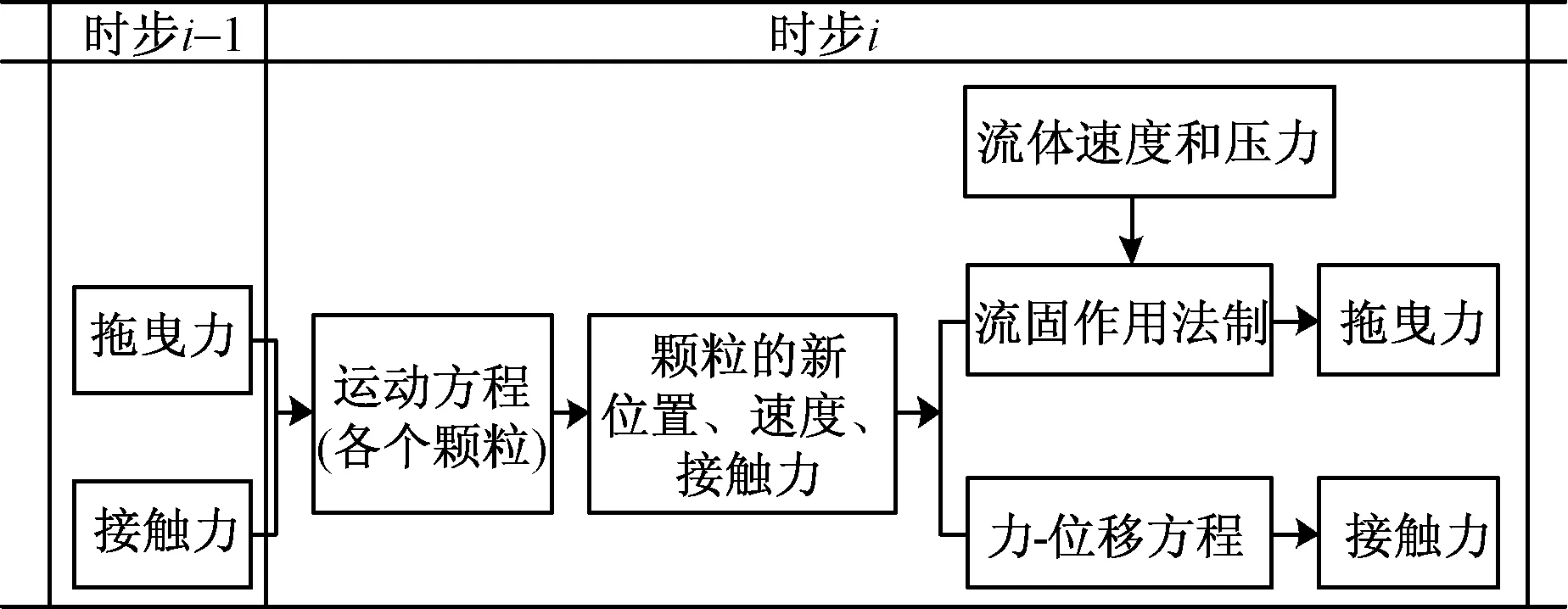
圖2 PFC3D流固耦合循環計算過程Fig.2 PFC3D fluid-solid coupling cycle computation process

2 數值模型建立

2.1 建模依據

中國西南和西北的河谷覆蓋層在縱向結構上多具有強、弱透水層交替層疊的特點，各層巖性、物理力學特性等差異較大，較有代表性是砂卵礫石和細砂互層結構如圖3(a)，各層取樣如圖3(b)、圖3(c)所示。

圖3 典型粗粒土及粗細相間的層狀覆蓋層Fig.3 Typical coarse grained soil and coarse and fine layered overburden

典型砂卵礫石層和細砂層的基本特征及透水性等級如表1所示。

表1 粗細粒土基本特征及透水性等級Table 1 Basic characteristics and permeability grade of coarse and fine-grained soil

根據上述典型的層狀粗粒土層，運用離散元軟件PFC3D來建立滲流水-土耦合模型，厘清顆粒運移規律。

2.2 數值模型生成及細觀參數標定

2.2.1 數值模型生成

為了更準確地對實際堤(壩)基中層狀粗粒土結構的滲透變形過程進行模擬，模型生成的顆粒必須能反映實際土體顆粒級配關系，實際土體中顆粒粒徑范圍(0.075～50 mm)較寬，如按照實際土體顆粒級配建立模型，將生成數量十分巨大的顆粒，導致計算效率降低甚至無法完成計算。因此，需對實際土體級配進行一定的近似處理，本文數值模型中顆粒最大最小粒徑分別取為10 mm和0.25 mm，由工程地質圖3及表1可知，上部土層為間斷級配的砂礫石土層，以2 mm作為粗細顆粒的區分粒徑，同時保持生成顆粒質量百分比與實際土體粗細顆粒百分比基本一致，近似處理后的土體級配如表2所示。應注意的是，該顆粒粒徑處理方法可能對試驗精度造成一定的誤差，但對滲透變形中顆粒運移過程的研究是可行的。此外，為降低顆粒模型中總的自由度，這里運用土工離心機試驗中的相似性原理，建立長×寬×高為120 mm×60 mm×60 mm的顆粒流模型如圖4所示。同時，為使建立的模型與實際土體的工程地質分層情況基本一致，利用PFC3D內置的fish語言編寫程序以生成不同土層，模型從上至下依次為：上部砂礫石層厚26 mm，中間細砂層厚6 mm，下部砂礫石層厚26 mm。此外，為防止上覆土層與模型上部墻體發生接觸沖刷，除管涌口外，在墻體上部邊界生成顆粒粒徑為2 mm規則排列的固定顆粒邊界。

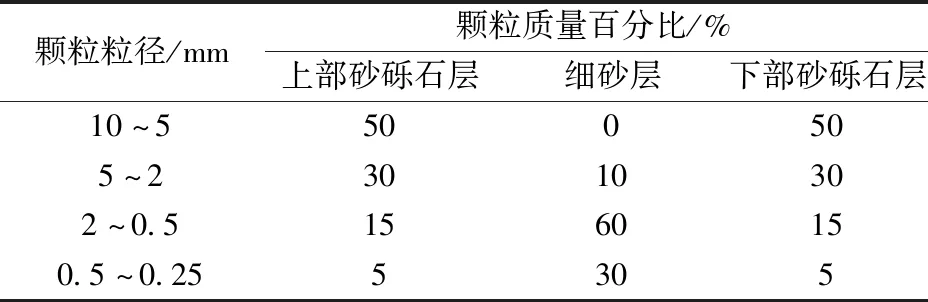
表2 PFC數值模型土樣參數Table 2 Soil sample parameters of PFC numerical model

圖4 堤(壩)基中多層粗粒土結構顆粒流模型Fig.4 Particle flow model of multi-layer coarse-grained soil structure in embankment (dam) foundation

2.2.2 細觀參數標定

為使所建模型能更有效的反映實際滲透變形過程，需要準確找出宏觀材料與細觀顆粒之間物理力學屬性的聯系。在利用PFC3D來模擬滲流破壞時，顆粒運動規律主要受到細觀參數摩擦系數的影響[10]，因此在數值模擬之前，必須對顆粒的摩擦系數進行標定，但顆粒宏-細觀參數之間存在較大的差異。研究表明，在散粒體材料中，材料的內摩擦角是其摩擦特性的綜合體現[11]，因此采用“反演模擬法”[12]來對顆粒的細觀摩擦系數進行標定，室內試驗測得砂礫石和細砂的宏觀內摩擦角分別為35°10′、26°30′，然后利用PFC3D進行三軸數值模擬試驗(圖5)，通過不斷調整顆粒細觀摩擦系數來獲取顆粒的細觀內摩擦角，將得到的細觀內摩擦角與宏觀內摩擦角進行對比，直到兩者接近或相等為止，最終得到粗礫和細砂的摩擦系數為1.25與0.79。模型具體細觀參數如表3所示。

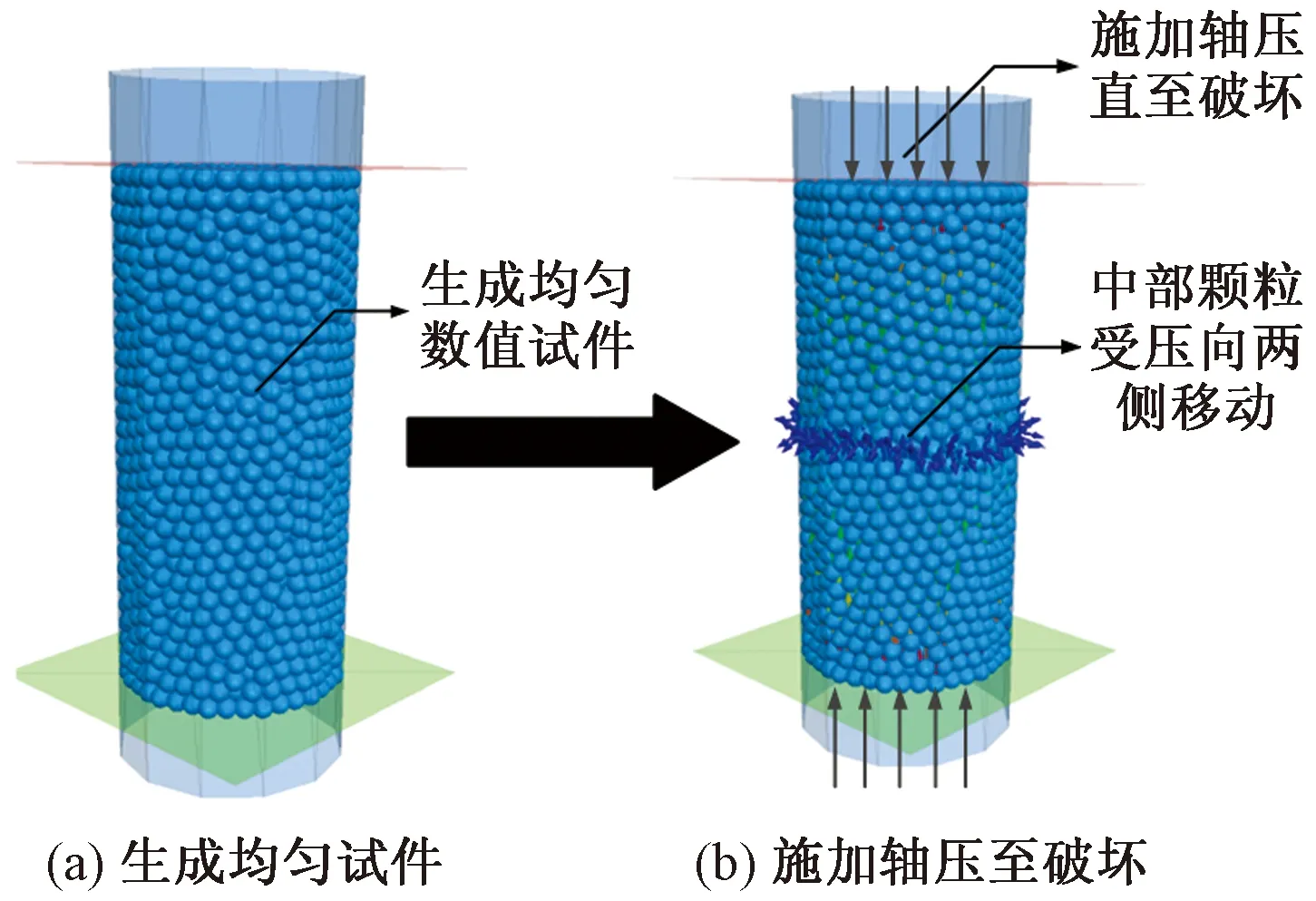
圖5 三軸數值模擬試驗Fig.5 Triaxial numerical simulation test

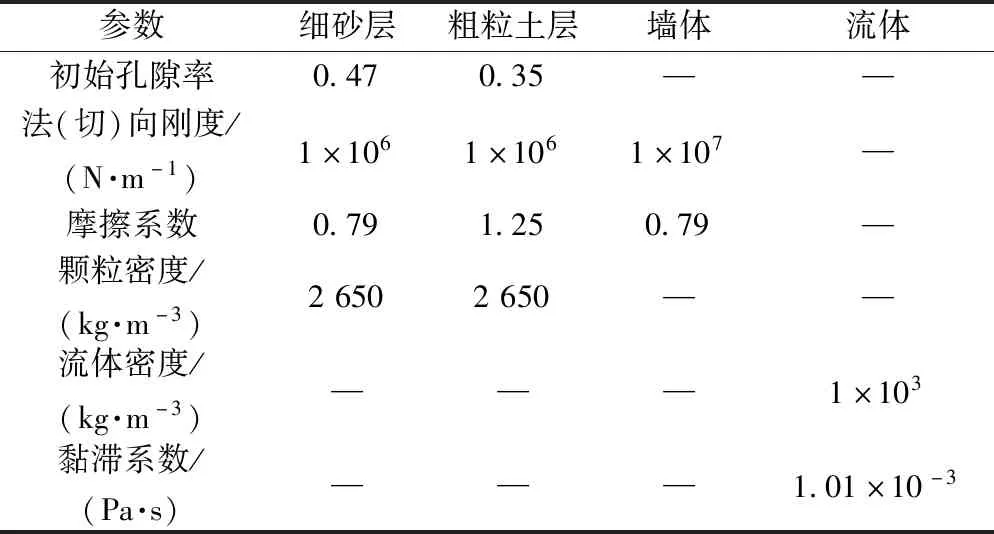
表3 PFC模型具體細觀參數Table 3 Specific meso-parameters of the model

參照表2及表3中模型細觀參數，利用PFC3D中fish語言編寫函數生成相應土層顆粒，各土層之間賦予線性接觸模型，采用半徑擴大法生成土顆粒，先將顆粒粒徑縮小，再將顆粒粒徑放大到指定的孔隙率，而后對土顆粒施加重力并進行循環計算，直至土顆粒間不平衡力較小或消除為止，以確保土層達到穩定狀態。

2.3 流體網格劃分及監測單元設置

PFC3D中運用固定粗糙網格法對流體進行處理，需將流體區域劃分為若干流體單元網格，且應確保所劃分的流體網格中均包含一定數量的顆粒。故考慮將整個模型沿長、寬、高方向分別劃分為8、4、4份，單個流體單元網格尺寸為15 mm×15 mm×15 mm。再進行流體計算之前，需對邊界條件進行設定，模型左側設定為施加水頭邊界，水頭壓力大小為100 kPa，上部、底部及側壁均設定為剛性不透水非滑移邊界，將模型上部X=12 mm、Y=39 mm、Z=24 mm處設置為零壓力流體出流口，出流口長寬為3 mm×3 mm[見圖6(a)]，該流體單元網格模型圖詳見圖6(b)。應注意的是，在左側邊界施加水頭之前，為避免流域內形成紊亂的流場，應首先將顆粒固定，然后施加水頭，直至流場趨于穩定，此后釋放顆粒，讓固體顆粒與流體進行作用。

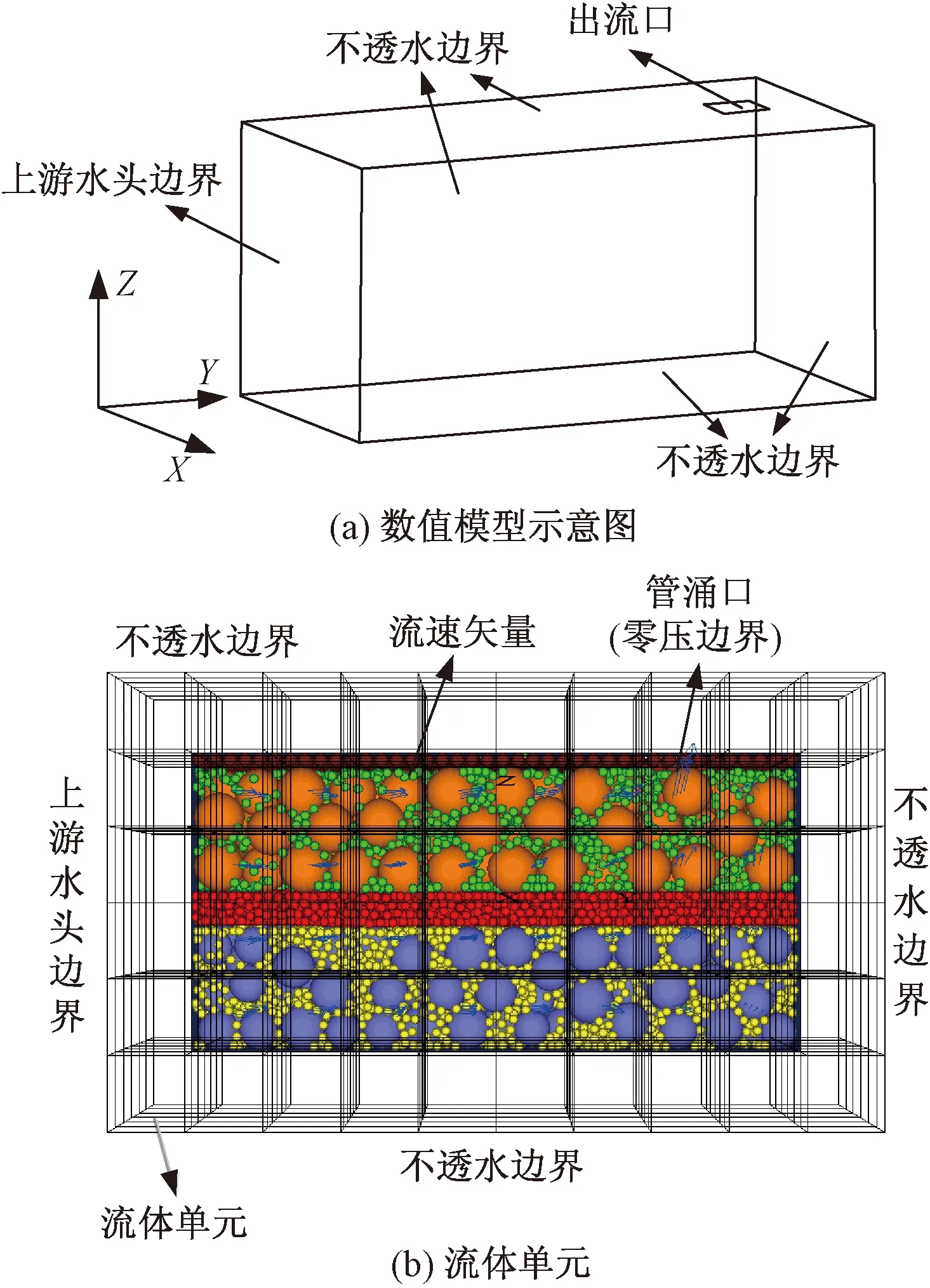
圖6 計算邊界及流體單元Fig.6 Computational boundary and fluid unit

在模型開始計算之前，為清晰記錄各土層不同部位顆粒流失的情況，分別在各土層設置以下監測區域，上部砂礫石層及細砂層從壓力上游端至下游端分別編號為S1、S2、S3、S4及Z1、Z2、Z3、Z4，如圖7所示，由于細砂層對下部砂礫石層起阻擋作用，導致下部砂礫石層顆粒很難發生流失，因此不對下部砂礫石層中顆粒流失進行監測。

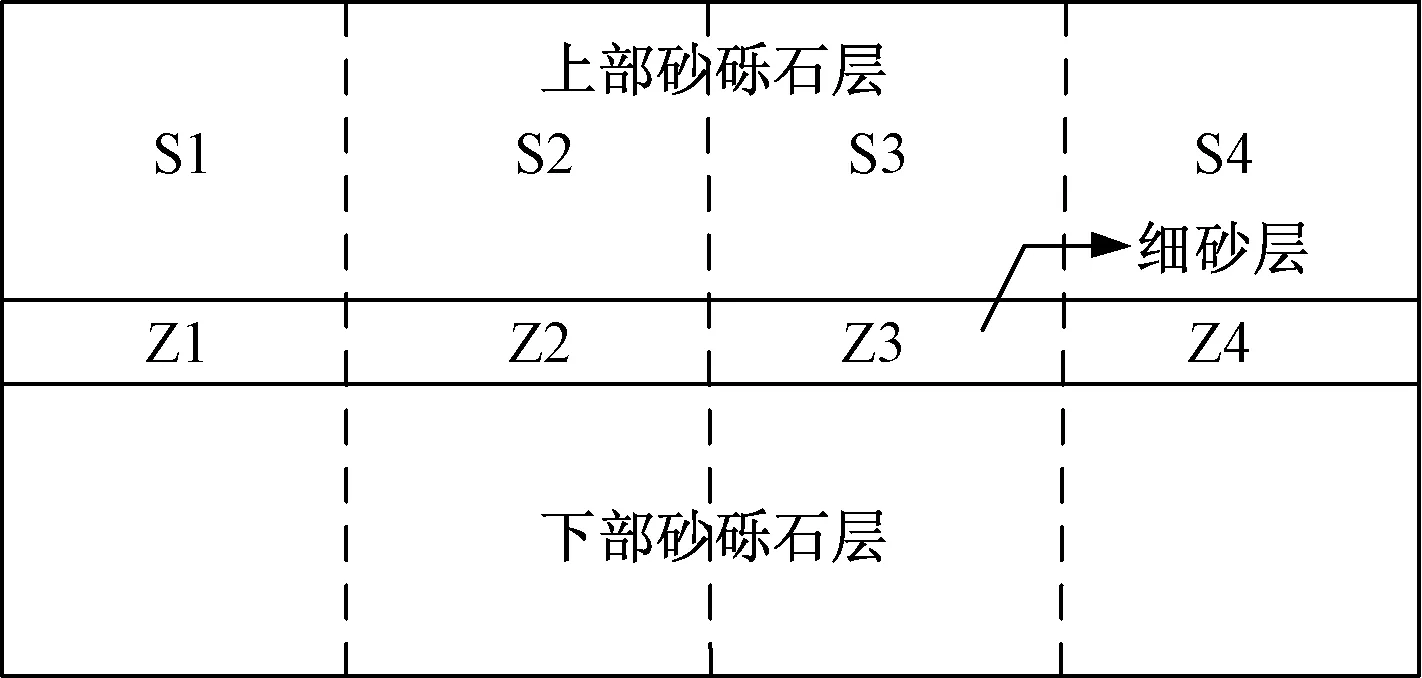
圖7 模型不同監測區域劃分Fig.7 Division of different monitoring areas in the model

3 數值試樣結果分析

3.1 上部砂礫石層滲透破壞過程

3.1.1 上部砂礫石層細顆粒遷移過程

該粗粒土層狀結構的上部砂礫石層中細顆粒遷移過程如圖8所示。

從圖8可以看出，因上部砂礫石為管涌型土，粗顆粒之間存在一定的孔隙，在初始水頭壓力作用下，上部砂礫石層中細顆粒從上游端逐漸向管涌口運移，上部砂礫石層中細顆粒在管涌口陸續流失，但并未出現顆粒整體流失及細砂層顆粒侵入上部砂礫石層中的現象 [見圖8(a)]。在計算時間步達到30萬步時，上部砂礫石層粗顆粒中細顆粒持續從上游端向管涌口處移動，導致在上游水頭S1區出現較大孔隙，在細顆粒移動過程中，有部分細顆粒因遇到較小孔隙而被阻擋形成阻塞區，此時，細砂層Z3和Z4區已有部分顆粒進入上部砂礫石層中，且由于S1區有較大孔隙出現，細砂層Z1區部分顆粒也開始進入上部砂礫石層中[見圖8(b)]。隨著計算時間步達到50萬步時，上部砂礫石層中細顆粒沿著粗顆粒間孔隙不斷從上游端向管涌口處移動，細砂層中顆粒進入上部砂礫石層中含量進一步增加，有部分顆粒已進入上部砂礫石層中部，以至于細砂層出現較大變形[見圖8(c)]。

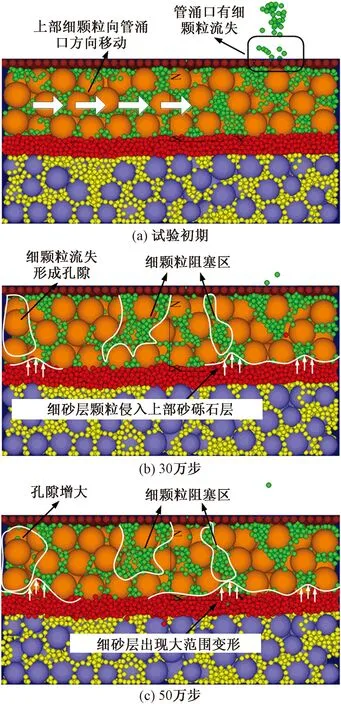
圖8 上部砂礫石層中細顆粒遷移過程Fig.8 Migration process of fine particles in upper gravel layer

3.1.2 上部砂礫石層不同區域細顆粒流失量

上部砂礫石層中不同區域細顆粒流失量隨計算時間步的變化曲線如圖9所示。顆粒流失量定義為該區域細顆粒流失的總體積與水頭壓力施加前該區域細顆粒總體積之比。

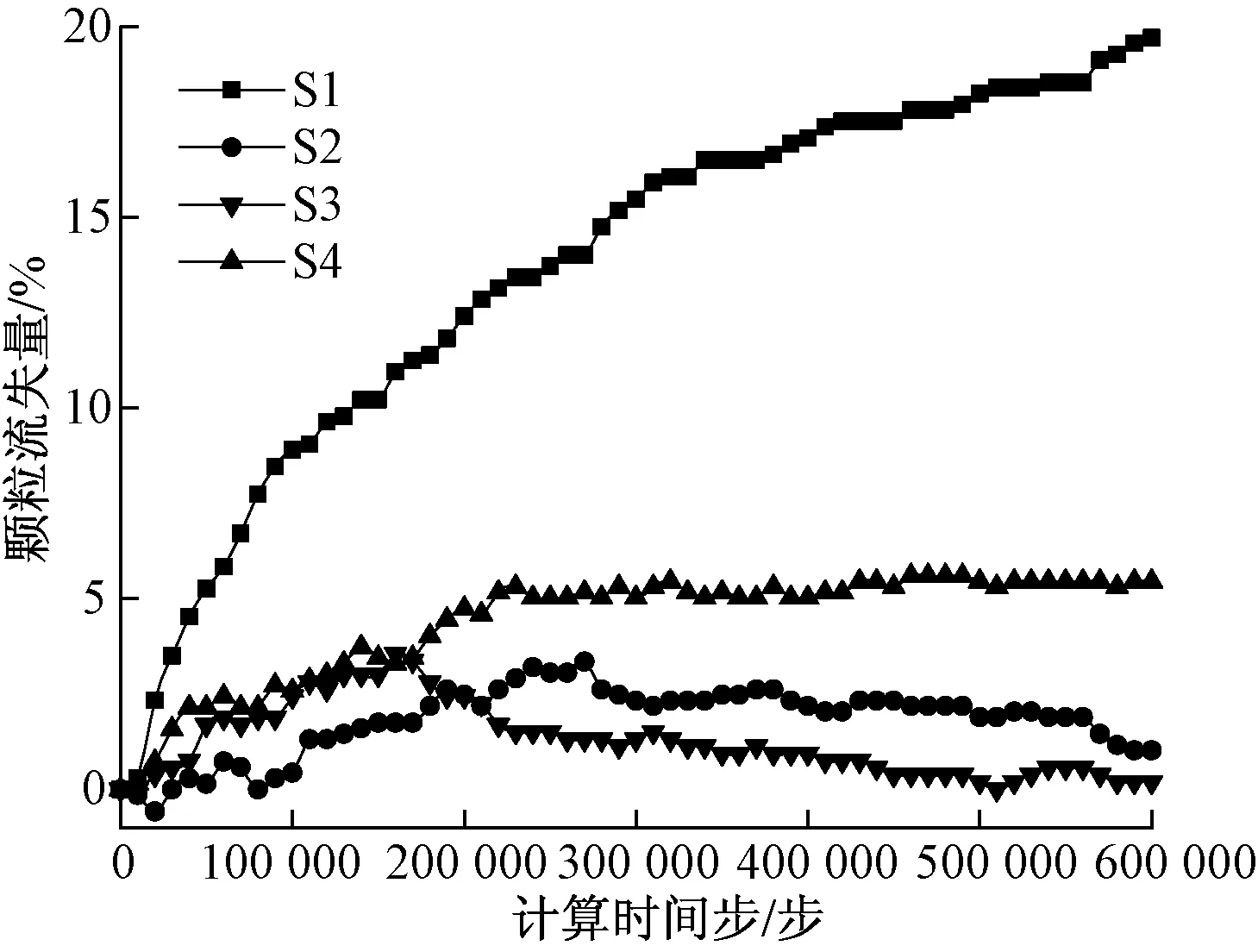
圖9 上部砂礫石層不同區域細顆粒流失量情況Fig.9 Fine particle loss in different areas of upper gravel layer

由圖9可知，在數值試驗過程中，上部砂礫石層上游端S1區細顆粒流失量最大，約20%，導致S1區粗顆粒間有較大孔隙形成。S2、S3區細顆粒流失量相對較少，當時間步增加至20萬步左右時，S2、S3區顆粒流失量分別增至3.5%、3%，而后直至計算結束，流失量分別降低至2.5%、1%，這是由于細顆粒從上游端流向管涌口處時逐漸在S2和S3區形成阻塞區所致。當時間步計算至25萬步時，S4區細顆粒流失量增至5%左右，之后隨時間步的增加，S4區顆粒流失量幾乎沒有變化，這是因為在試驗初期管涌口顆粒不斷流失，隨著時間步的增加，上游端細顆粒持續流向管涌口，同時，細砂層顆粒陸續進入上部砂礫石層中，導致S4區細顆粒流失量逐漸減少直至幾乎不變。

通過對上部砂礫石層中細顆粒遷移現象及流失曲線分析可知，在滲透力作用下，上部砂礫石層中細顆粒在粗顆粒孔隙間移動而后被帶出土體外，逐漸形成穩定的管涌通道，屬于典型的管涌破壞。

3.2 細砂層滲透破壞過程

3.2.1 細砂層顆粒遷移過程

該層狀結構中的細砂層中顆粒遷移過程如圖10所示。

圖10 細砂層中顆粒遷移過程Fig.10 Particle migration in fine sand

從圖10(a)可清晰觀察到，在施加水頭壓力初期，細砂層顆粒幾乎沒有發生。如圖10(b)所示，隨著計算時間步增加至30萬步，細砂層中上游端Z1區及管涌口附近Z3及Z4區顆粒已部分侵入上部砂礫石層中，甚至在管涌口正下方細砂層Z4區已有少許顆粒進入上部砂礫石層中部，這是由于上部砂礫石層中細顆粒的逐漸流失，給予了細砂層進入上部砂礫石層的空間。當時間步進一步增加至50萬步過程中，細砂層Z1、Z3及Z4區處顆粒進入上部砂礫石層中越來越多，且在細砂層Z4區已有一些顆粒流失至管涌口附近，隨著顆粒持續流失，導致細砂層逐漸出現小范圍的變形[見圖10(c)]。

3.2.2 細砂層不同區域顆粒流失體積

細砂層不同區域進入上部砂礫石層顆粒流失體積隨計算時間步的變化曲線如圖11所示。

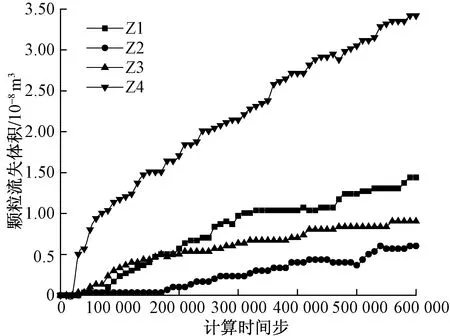
圖11 細砂層不同區域顆粒流失體積變化Fig.11 Variation of particle loss volume in different areas of fine sand bed

由圖11可知，在數值試驗計算過程中，細砂層在管涌口下方Z4區處顆粒持續流失并且流失顆粒含量最多，約3.5×10-8m3，其余區域顆粒流失量相對較少。在數值試驗初期，僅有曲線S4隨時間步的增加而增加，而其余曲線無明顯變化，表明細砂層最先在管涌口正下方Z4區處出現顆粒流失。隨著計算時間步的增加至30萬步，曲線Z1、Z2及Z3均隨著計算時間步的增加而增加，說明Z1、Z2及Z3區顆粒都已發生流失，且在此過程中，可見Z2區顆粒是最后發生流失的，這是由于上部砂礫石層S2區有阻塞區形成，阻礙了細砂層顆粒的進入。當計算時間步增加至50萬步時，曲線Z1隨時間步緩緩增加，對應細砂層Z1區顆粒流失量逐漸增多，這是因為上部砂礫石層中上游端S1區細顆粒逐漸流失，以至形成較大孔隙，給予了Z1區顆粒進入上部砂礫石層空間。

通過對中間細砂層中顆粒遷移現象及流失曲線分析可知，細砂層中顆粒最先在管涌口正下方Z4區發生流失，其余區域顆粒流失相對較晚，且顆粒流失量均隨著計算時間步的增加而增加，導致細砂層出現小范圍的變形。

3.3 上部砂礫石層下沉量

如圖12所示為上部砂礫石層下沉量隨計算時間步的變化曲線，下沉量定義為上部砂礫石層顆粒垂直向下方向運動距離總和。從圖12中可以看出，隨著計算時間的增加，上部砂礫石層的下沉量逐漸增加至0.012 m，這是由于細砂層中顆粒不斷流失所致，這種情況下當上部砂礫石層細顆粒含量流失達到一定程度，隨著管涌通道的貫通而發生破壞，將對上部建筑物產生重大危害。通過顆粒流模擬，上部砂礫石層及細砂層所表現出的滲透破壞現象，這與劉杰[13]對間斷級配土滲透破壞機理試驗研究所得結論相吻合。

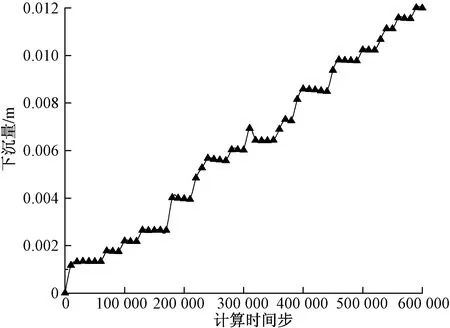
圖12 上部砂礫石層下沉量Fig.12 Subsidence of upper gravel layer

4 結論

在PFC3D細觀參數標定時，采用“反演模擬法”，較準確地建立了材料宏觀參數與顆粒細觀參數間聯系，有效的模擬了多層粗粒土層滲透變形的發展過程，獲得了堤(壩)基滲透變形中顆粒流失及下沉量等情況，為此類地基的滲透破壞的研究提供了一定參考，并得到以下結論。

(1)滲透破壞主要發生在上部砂礫石層中，隨著滲透破壞的持續發生，逐漸影響下部土層；作為滲流出口的上部砂礫石層，該層中細顆粒在粗顆粒孔隙間移動而后逐漸被帶出土體外，逐漸形成穩定的管涌通道，具有明顯的溯源性。

(2)隨著計算時間的增加，上部砂礫石層的下沉量逐漸增加，當上部砂礫石層細顆粒含量流失達到一定程度，堤(壩)基發生破壞，將對上部建筑物產生重大危害。

(3)中間細砂層在上部砂礫石層管涌破壞后，其顆粒最先在管涌口正下方Z4區發生流失，其余區域顆粒流失相對較晚，且顆粒流失量均隨著計算時間步的增加而增加，導致細砂層出現小范圍的變形出現。

(4)由于幾何條件不滿足，在上部土層不發生明顯破壞的情況下，不會對深層的砂礫石層顆粒運移造成影響。

綜上，上部強透水層是滲透破壞的關鍵區域，在實際工程中應重點處理；深層次的強透水層對堤壩基滲透破壞的貢獻較小，在上部土層不發生破壞的情況下，深部土層一般不會發生顆粒流失現象。