Scratch用遞歸畫謝爾賓斯基三角形

Intoweb

遞歸是學習編程中的一個難點，它的含義是：編程語言中，函數直接或間接調用函數本身，則該函數稱為遞歸函數。

換個通俗說法就是：從前有座山，山上有座廟，廟里有個老和尚給小和尚講故事，故事講的是：從前有座山……這樣講下去是不是沒有盡頭了，在實際編程中遞歸要設置一個遞歸出口，否則就成了死循環。

另外俄羅斯套娃也可以看作遞歸，娃娃里面套著娃娃……直到最小的娃娃（遞歸出口）。

初步了解了遞歸思想后，我們通過畫分形圖來體驗一下遞歸的效果。

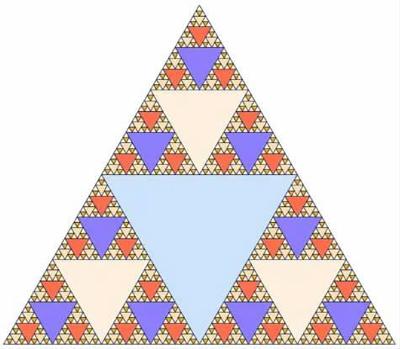
謝爾賓斯基三角形（Sierpinski triangle）是一個優美的分形圖案。從一個大三角形開始，連接每一個邊的中點，將大三角形分為四個小三角形，然后挖掉中間的三角形，依次對其余三個三角形重復執行上述操作，用Python繪制的效果如圖1，為了區分不同層級的三角形使用了不同的顏色。因為對三角形不斷重復進行分割操作，使用遞歸就能讓計算機畫出這個圖形了。

這是Scratch 繪制謝爾賓斯基三角形的代碼（如圖2）。由于遞歸函數需要引用本身，所以必須要用到自定義積木，這樣就可以在自定義積木中插入自身完成遞歸。

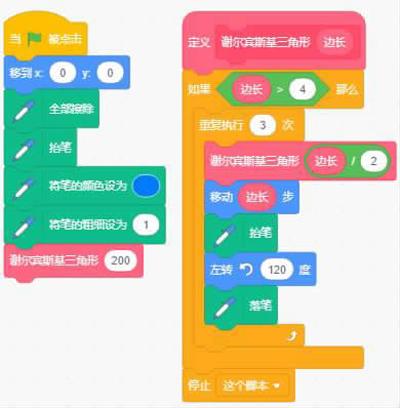
1. 自定義積木“謝爾賓斯基三角形（邊長）”。首先判斷如果邊長>4就繼續執行，因為理論上后面的步驟2和3可以無限重復下去，就代碼而言，必須要保證算法的有窮性，通過設置邊長的最小值，程序就可以按需要終止。根據Scratch畫筆的精度，最小的三角形邊長大于4時，圖形效果較好。你可以自行試驗最小邊長為3的效果，最小的三角形成實心的了。如圖3從左到右，不斷細分的謝爾賓斯基三角形（如圖3）。

2. 重復執行3次，移動“邊長”，左轉120度，畫出一個三角形。

3. 為了畫出更小一級的三角形，調用自身，并將邊長除以2。因為在重復執行3次的循環內，所以可以畫出3個二分之一“邊長”的三角形。

4. 由于遞歸引用，所以三角形邊長會持續減半，實際執行時設置邊長為200，會從最小邊長為6的三角形開始畫，逐漸畫出最大邊長200的三角形。實際繪制效果，如圖4。

通過繪制謝爾賓斯基三角形，我們初步接觸了在自定義積木中引用本身的結構。這就是遞歸函數。遞歸概念是比較難以理解和用好的。未來我們將繼續對這個概念進行更深入的學習。