Scratch趣味數學之雞兔同籠
2020-06-30 14:33:35陳新龍
電腦報 2020年19期
關鍵詞:解題
陳新龍
雞兔同籠出自《孫子算經》:“今有雉兔同籠,上有三十五頭,下有九十四足,問雉兔各幾何?”題目意思是:有若干只雞兔同在一個籠子里,從上面數有35個頭,從下面數有94只腳,求籠中各有多少只雞和兔。那么Scratch中我們應該怎么編程呢?
雞兔同籠是中國數學最經典的題目,直到現在,小學生也要遇到雞兔同籠問題。今天就用三種不同的算法來解決雞兔同籠。
首先設置四個變量分別為總腳數、總頭數、兔數、雞數。
1. 最萬能的方程法
設雞數為X只,則兔數有35-X只,2X+4(35-X)=94,解出X=23,則兔數=35-23=12只(如圖1)。
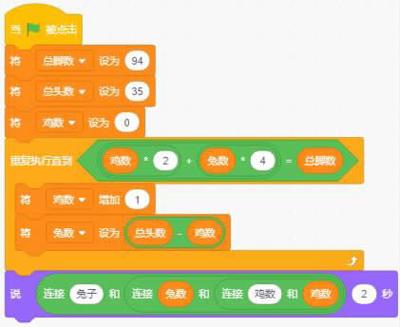
2. 抬腿法:總腳數94只,假設先命令籠子里的動物全部抬起兩條腿,因為雞是兩只腳的動物,所以雞的腳都被抬起來了,相當于這時候雞的腿沒有了,只剩下兔子剩下兩只腳站地上。94-35-35=24,剩下的都是兔子的腳數,24/2=12得出兔數,則雞數=總頭數-兔數=23(如圖2)。
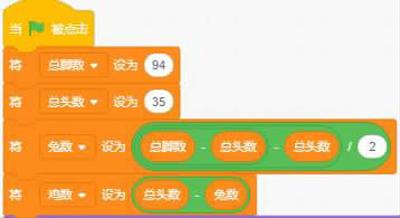
公式:(總腳數-總頭數-總頭數)/2=兔數
3. 砍腿法:砍掉雞的一只腳,砍掉兔子的兩只腳(相當于砍掉動物一半的腳),94/2=47,剩下47只腳,再減35,則雞又砍掉一只腳,兔子又砍掉一只腳,這時候雞已經沒腳可以砍了,還剩下兔子的腳。47-35=12,則得出兔子一共12只。雞數等于35頭數減去兔數,雞數=35-12=23只(如圖3)。
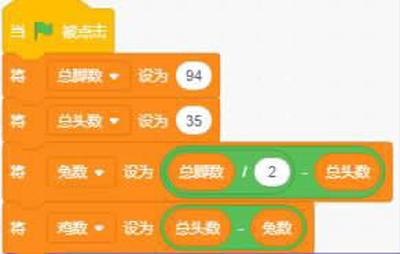
公式如下:兔數=總腳數/2-總頭數=94/2-35=12
雞數=總頭數-兔數=35-12=23
雞兔同籠是一個很經典的題目,解題的算法也很多,本題的關鍵在于怎樣把數學的解題方法變成編程的算法寫成代碼。比如解方程法就是將X從0一直試算到符合條件為止。這里我用了三種不同的方法,其實遠不止這三種,大家課后可以找一下相關的資料然后用Scratch編新的算法。
猜你喜歡
小學生學習指導(低年級)(2022年9期)2022-10-08 03:12:02
中學生數理化·中考版(2022年8期)2022-06-14 06:55:52
小學生學習指導(低年級)(2021年4期)2021-07-21 01:59:26
中學數學雜志(2019年1期)2019-04-03 00:35:46
中學生數理化·中考版(2018年11期)2019-01-31 06:18:02
數學小靈通·3-4年級(2017年12期)2018-01-23 03:37:54
數理化解題研究(2017年4期)2017-05-04 04:07:56
讀寫算(下)(2016年11期)2016-05-04 03:44:22
中學生數理化·八年級數學人教版(2016年3期)2016-04-13 09:17:06
中學生數理化(高中版.高二數學)(2016年10期)2016-03-01 03:46:37

