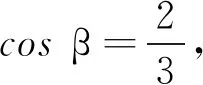質點沿半球面下滑問題研究

李開瑋

(廣東理工學院工業自動化系 廣東 肇慶 526100)

在文獻[1]中，作者探討了斜面不固定時，滑塊的運動規律，在斜面問題中，斜面的傾角始終不變，本文將研究質點沿半球面下滑的問題.

1 問題來源

如圖1所示，質量為M，半徑為R的光滑半球固定在水平面上，一質點m由球面頂點從靜止開始下滑，求質點與球面分離時的位置、速度．

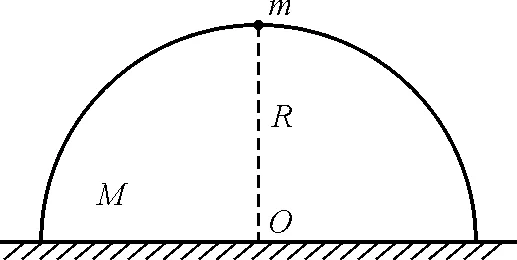
圖1 問題示意圖

分析：如圖2所示，假設質點速度為v，質點與球心連線與豎直方向夾角為θ，球面對質點支持力為N.

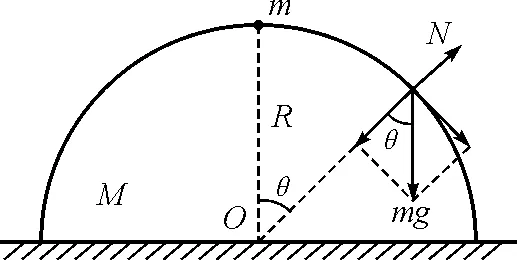
圖2 質點受力分析

對質點根據受力分析有

(1)

由式(1)得

(2)

當質點與球面分離時N=0，這時有

(3)

聯立式(2)、(3)可得，質點與球面分離時

當半球面不固定，水平面光滑時，質點將在什么位置與半球面分離？

2 問題擴展與討論

如圖3所示，當半球面不固定時，質點沿半球面下滑，半球面必然沿水平面向左運動，設質點與球心連線與豎直方向夾角為β，m相對于球面線速度為v1，相對于地面水平速度為v3x，豎直速度為v3y，M相對于地面速度為v2，則根據相對運動關系有

v3x=v1cosβ-v2

(4)

v3y=v1sinβ

(5)

圖3 球面不固定時，質點運動示意圖

對系統，根據功能原理有

mgR(1-cosβ)=

(6)

由于水平面光滑，根據動量守恒有

mv3x=Mv2

(7)

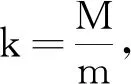
(8)

(9)

當m與M分離時，m對M壓力為零，此時M水平方向不受任何外力，受力平衡，因此這個瞬間，半球面為慣性參考系，此時對m，以半球面為參考系，根據圓周運動規律有

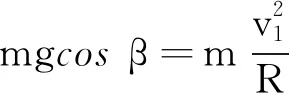
(10)

聯立式(8)、(10)可得

cos3β-3(k+1)cosβ+2(k+1)=0

(11)

由式(11)可知β與半球面跟質點的質量之比k有關，當k=1時，式(11)變為

cos3β-6cosβ+4=0

(12)

解式(12)得

3 結束語