基于特征優化的BP神經網絡在電動汽車價格上的預測研究

劉佳麗 趙小敏

(南通大學交通與土木工程學院 江蘇 南通 226019)

一、引言

(一)背景及意義

隨著可持續化發展得到大力倡導，21世紀在汽車領域發展的終點將結合環境問題、能源問題和交通擁堵問題來進行研究，整個汽車行行業的發展將呈現出節能化、智能化、信息化的局面。新能源汽車中，純電動車的發展前景十分廣闊，優勢明顯。隨著電動汽車的推廣，許多消費者開始將目光轉入購買電動汽車以取代傳統的燃油汽車，這時候建立一套電動車價格預測模型顯得尤為重要，以便于消費者以科學的標準去了解電動汽車的定價。文中首先對所給的電動車數據集進行數據預處理，篩選數據中需要修改和剔除的數據，并將數據進行歸一化和特征值篩選等數據處理工作，隨后建立BP神經網絡對處理后的數據進行數據訓練，通過確定最優的模型參數對模型進行調試，然后對所給的未知價格的電動車數據進行價格預測，并給出結果。

(二)價格預測模型研究現狀

目前所有的價格預測模型中，大體分為兩類價格預測模型，分別為時序價格模型和非時序價格模型。時序價格模型的主要特點是商品的價格隨著時間進行著波動，比如蘋果價格的預測，此類商品的價格隨著時間具有較大的波動變化，劉斌[1]在針對傳統的農產品價格模型無法對蘋果市場的價格波動進行預測的問題，提出了一種基于分布式神經網絡的蘋果價格預測模型；隨著時間進行變化的還有房產價格的變化，趙泰[2]以青島市近8年商品房銷售價格為基礎，通過建立GM(1,1)模型預測商品房價格走向，對房地產市場的宏觀調控及工作的開展有著重大意義。非時序價格模型的主要特點是價格的定價主要是受制于其自身的特征相關，比如原材料、成本、具有的功能等，劉蕾[3]在分析顧客需求與銷售商策略間基本關系的基礎上，從期望銷售利潤最大化的角度，構建了銷售商的最優定價模型；梁肖裕[4]通過對多元回歸定價模型進行檢驗,使用SVM支持向量機解決平臺中的任務合理定價問題。

目前主流的神經網絡預測模型有許多，例如RNN，LSTM，BP，GRU等等，由于本題的主要目的是根據電動汽車的商品參數確定其價格登記，與時間序列無關因此LSTM、GRU等模型并不合適，并且其參數為一維數組，相鄰的參數之間并不存在特殊聯系，因此RNN等模型也不合適，所以我們采用BP神經網絡進行電動汽車價格預測。

二、BP神經網絡

(一)模型原理

BP神經網絡(Back Propagation Neural Network)是一種使用誤差逆傳播算法進行訓練、測試、仿真的多層前饋神經網絡，是當前在研究和科學應用中較為廣泛的神經網絡模型之一[7]。BP神經網絡可以對采集的數據樣本進行非線性函數關系映射，對信息處理具有自組織、自學習、知識推理等特點，對非確定規律性系統具有自適應特征，通過建立的映射關系揭示其內在規律、特征。

BP神經網絡的學習訓練和建模規則是使用最速下降算法，通過誤差反饋的反向傳播從而不斷調整BP神經網絡各層神經元的權值和閾值，使得BP神經網絡的均方誤差最小。在前向傳播過程中，輸入信號從輸入層經隱含層逐層處理，直至輸出層，產生輸出信號，每一層的神經元狀態只影響下一層的神經元狀態；若輸出信號不能滿足期望輸出要求，則轉入誤差反向傳播過程，根據預測誤差從輸出層開始到輸入層，不斷修正網絡的權值和閥值，從而使BP 神經網絡的預測輸出不斷逼近期望輸出。

BP神經網絡的模型結構包括：輸入層(input)、隱藏層(hide layer)和輸出層(output layer)。標準的BP神經網絡模型結構如圖1所示。BP神經網絡的每一層的預測公式為O=IW+B其中O為該層的輸出，I為輸入函數，W為模型的參數矩陣，B為模型的參數偏置。

圖1 標準的BP神經網絡模型結構

(二)BP神經網絡在價格預測中的應用

針對電動汽車價格預測模型表現出來的非時序的特點，通過對電動汽車的不同特征進行篩選，研究BP神經網絡在價格預測中的應用。BP 神經網絡是一種復雜的智能信息處理技術，有著強大的非線性處理能力，也有著良好的自組織性、適應性以及學習能力和抗干擾能力，非常擅長處理非線性復雜問題，并且它能發揮訓練速度快的優勢，能自動從歷史數據中提取有關活動的信息，可以克服傳統定量預測方法的許多局限和困難，同時能避免人為的影響，因而為電動汽車的價格建模和預測提供了很好方法，預測準確率比傳統統計方法高。黃山[5]基于BP神經網絡的隨機信號預測方法,利用三種國際貨幣匯率價格的歷史數據作為參考,對未來匯率價格進行短期預測；孫婷婷[6]基于特征選擇方法提取影響房價變化的典型經濟要素；然后針對房價要素特點構建BP網絡模型，通過已有數據對BP神經網絡模型進行深度訓練和校驗，預測房屋價格的走勢。

(三)預測流程

通過建立BP神經網絡模型對電動汽車價格進行預測，首先需要對數據進行數據預處理，篩選出有效特征值，并對數據進行歸一化處理，將處理完的數據用于數據模型訓練。BP神經網絡模型在進行預測前需要進行模型的訓練，將文中所給的電動車的數據進行劃分，分為訓練集和測試集，訓練集的數據用來對模型進行訓練，測試集的數據用來對模型的訓練效果進行測試，通過數據的訓練可以使網絡具備聯想記憶和預測能力。圖2所示的是具體算法流程圖。

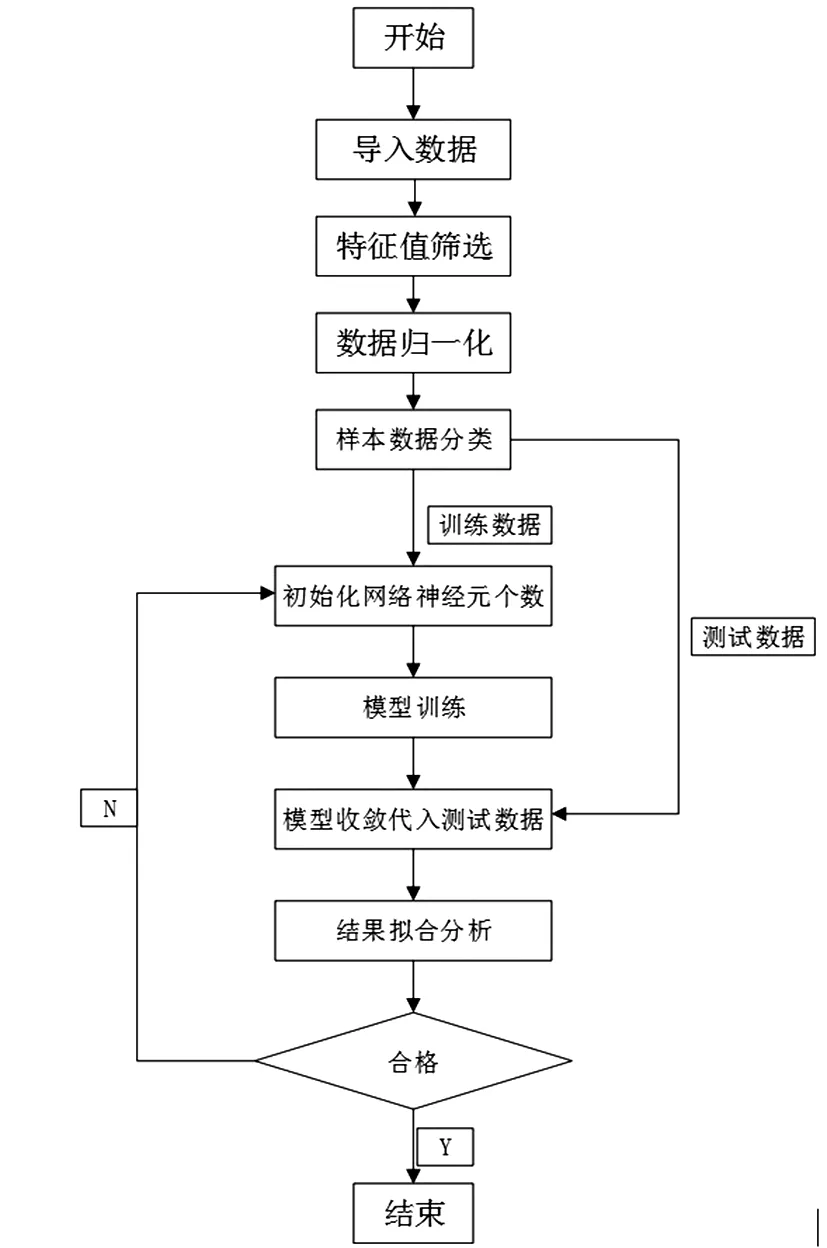
圖2 算法流程圖

三、電動汽車價格預測模型

(一)數據來源

通過結合某品牌電動汽車給出了不同規格的電動車屬性與價格數據建立價格預測模型進行分析，該數據集中存在已知價格的訓練數據和未知價格的預測數據，通過建立預測模型挖掘屬性與價格之間的關系預測這批未知價格電動車的價格。

(二)數據處理及評價標準

1.回歸特征篩選

特征選擇(Feature Selection)也稱特征子集選擇(Feature Subset Selection,FSS)，或屬性選擇(Attribute Selection)。是指從已有的M個特征(Feature)中選擇N個特征使得系統的特定指標最優化，是從原始特征中選擇出一些最有效特征以降低數據集維度的過程，是提高學習算法性能的一個重要手段，也是模式識別中關鍵的數據預處理步驟。

灰色關聯度分析是一種多因素統計分析法，主要根據各因素變化曲線幾何形狀的相似度來判斷因素之間的關聯度大小，在進行分析時需要比較研究對象與待識別對象之間的曲線貼近程度，并分別量化，計算出研究對象與待識別對象之間的關聯度，進而通過比較各關聯度的大小來判斷待識別對象對研究對象的影響程度[8]。簡單來說，當對某個系統進行灰色關聯度分析時，先要確定使用的關聯度模型，選好參考序列、比較序列，然后計算關聯度，最后按關聯度的大小進行排序和分析并得出結論。為進一步剖析電動汽車價格與其影響因素之間的相關性，選取價格為參考序列，feat(1-20)為比較序列，并利用灰色關聯度分析法計算各比較序列與參考序列之間的關聯度，各特征之間的關聯度分析表見圖3。為了更直觀的展現電動汽車各特征指標與price之間的關聯度，我們將第20列數據單獨取出，并按影響因素從大到小排序生成圖4的灰色關聯度特征值篩選圖。

圖3 各指標之間的影響程度

圖4 各指標對價格的影響程度

發現數據集所給的20個指標中第14個指標“以兆字節為單位的隨機存取存儲器”對price的影響程度最高為0.81，其余指標對price的影響均在0.6左右均不可忽略，因此通過該節的分析，將使用全部的20個指標對price進行價格預測。

2.標準化處理

圖5 未做標準化的訓練過程

在對數據進行預測之前，首先對數據進行標準化處理，在深度學習領域中，不同數據特征評價指標往往具有不同的量綱和量綱單位，這種情況會影響到數據預測的結果，為了消除指標之間的量綱影響，需要進行數據標準化處理。圖5展示的是未做標準化的訓練過程，可以看出，由于數據的量綱差距過大，導致訓練過程不收斂，因此標準化處理必不可少。

目前最常用的是Min-Max標準化和Z-Score標準化。Min-Max標準化又稱0-1標準化(0-1 Normalization)/ 線性函數標準化 / 離差標準化是對原始數據的線性變換，使結果落到[0,1]區間，轉換函數如下：

其中max為樣本數據的最大值，min為樣本數據的最小值。圖6展示的是標準化處理后的訓練過程，很明顯進行標準化處理之后訓練的效果得到了極大的改善。但這種方法有一個缺陷就是當有新數據加入時，可能導致max和min的變化，需要重新定義。

圖6 max-min標準化的訓練過程

Z標準化也叫標準差標準化，是SPSS中最為常用的標準化方法，SPSS默認的標準化方法就是Z-Score標準化。這種方法給予原始數據的均值(Mean)和標準差(Standard Deviation)進行數據的標準化。經過處理的數據符合標準正態分布，即均值為0，標準差為1，其轉化函數為：

其中μ為所有樣本數據的均值，σ為所有樣本數據的標準差。Z-Score標準化方法適用于屬性A的最大值和最小值未知的情況，或有超出取值范圍的離群數據的情況。該種標準化方式要求原始數據的分布可以近似為高斯分布，否則標準化的效果會變得很糟糕。圖7展示Z標準化下的訓練效果。

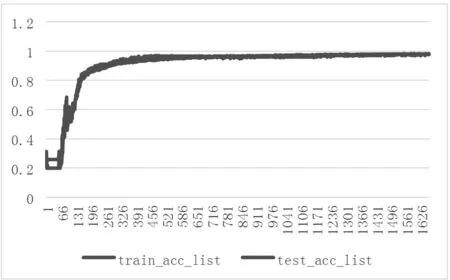
圖7 Z-Score標準化的訓練過程

由于本題中會新加入測試集的數據，會導致樣本部分指標的max值和min值產生波動所以并不適用于Max-Min標準化，并且Z-score標準化后收斂后的準確率也更高，我們采用Z-score對數據進行標準化處理。

(三)參數選取

一般來說，訓練BP神經網絡模型靠增加隱層節點數來獲得較低的誤差的訓練效果，要比通過增加隱層數來降低誤差更容易實現[9-10]。因此在本文構建的神經網絡中只考慮3層網絡(即只有1個隱藏層)的網絡進行訓練，下面我們將討論激活函數以及隱藏層個數的選取。

1.激活函數選取

目前常用的激活函數有Sigmod、Tanh、Softmax、Relu等，由于本題的輸出結果共分為0、1、2、3四類，屬于多分類問題，因此從隱藏層到輸出層的激活函數選用Softmax。當輸出總共有n類時，第j類的概率為：

Sigmod函數常用與隱藏層的輸出，在特征相差比較復雜的情況下效果比較好因此，我們選用Sigmod函數作為隱藏層到輸入層的激活函數。Sigmod函數為：

圖8 Sigmod函數圖

2.隱藏層元素個數以及訓練次數選取

將隱藏層元素的個數分別設置為5個，10個，15個以及20個訓練次數設置為2000次分別進行訓練，其準確率(ACC)隨訓練次數的變化如下由于中間部分過于一致，將從前200次以及擬合之后的情況進行討論。通過訓練發現在隱藏層元素不同的情況下收斂的速度相近，大約都在150次之后收斂，大約在800次左右收斂穩定，訓練的效果無法再繼續提升，收斂穩定之后的準確率也相近，均穩定在97%到99%之間，隱藏層元素個數為10的情況下收斂后的準確率最高，因此將隱藏層元素的個數定位10個，訓練次數定為800次。

圖9 前200次訓練過程

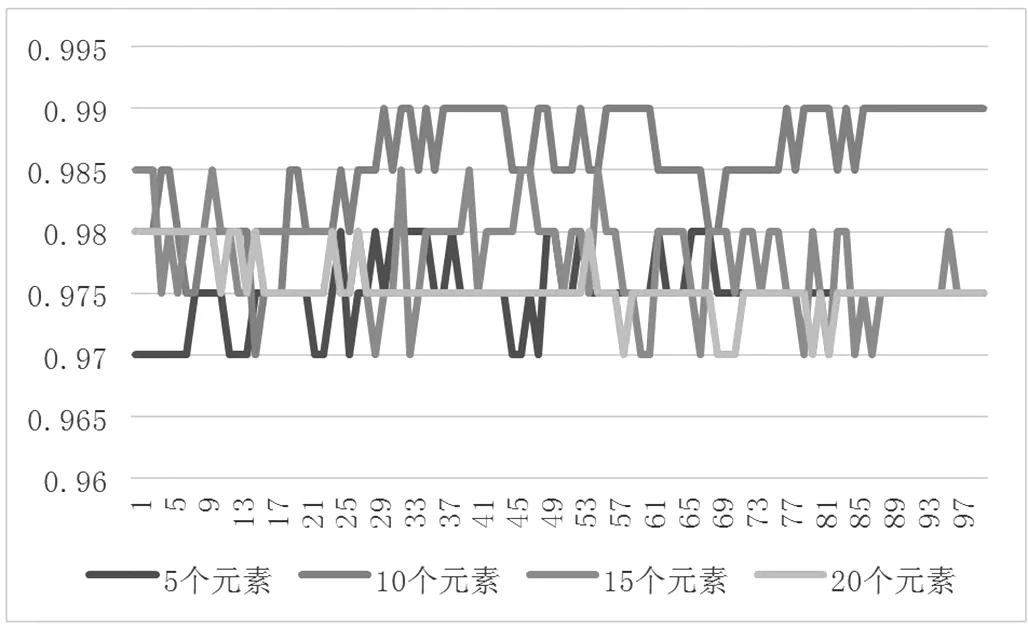
圖10 擬合后的訓練結果

(四)預測結果及分析

將上節中確定的參數以及訓練模型進行訓練，最終訓練的過程如圖11所示，訓練效果如圖12所示，部分預測結果如表1所示。采用R-Square作為訓練效果的評價指標，預測的準確率約為98%，并與LSTM模型進行比較，表2展示的是預測對比情況。

圖11 最終訓練的訓練過程

圖12 訓練效果

表1 部分預測結果

序號idPredict_priceTrue_price0150111115020021503113150401415051051506116150733

表2 預測結果評價

四、結論

通過對某品牌電動汽車所給的不同規格的電動汽車屬性和價格數據進行數據分析與模型搭建，構建了一套用于電動汽車價格預測的BP神經網絡模型。首先對BP網絡模型在價格預測中的適用性情況進行了分析，確定了BP神經網絡模型在電動汽車價格預測中具有良好的適用性。隨后對原始數據進行灰色關聯度分析，進行關鍵特征值篩選，通過分析得出，在給出的數據集中，20個特征值都具有一定的權重影響因子，對模型的最終預測結果都有相應的作用。隨后將特征值篩選后的數據進行歸一化處理，并搭建BP神經網絡價格預測模型對價格未知的數據集進行預測，通過最后的數據擬合情況和預測成功率為98%。可知，基于特征優化的BP神經網絡在電動車價格預測上具有很好的實用性。