含分布式電源的城市電網故障分析方法研究

馬子欽，廖 凱，楊健維

(西南交通大學電氣工程學院，四川 成都 610031)

0 引 言

隨著全球化石能源短缺、溫室效應加劇，大力發展可再生能源成為了城市電網發展的主要趨勢。其中以風能、太陽能為主的分布式電源逐漸接入城市電網，而分布式電源出力具有隨機性，這對電網故障時的潮流情況帶來了不確定性影響，使得傳統故障分析方法難以適應[1-2]。故障分析方法是保護配置的基礎，因此分布式電源出力的隨機性有必要在故障分析中深入考慮，以得到更為準確的故障分析結果，保障城市電網的可靠安全運行。

分布式電源常通過電力電子器件接入電網，即逆變型分布式電源。目前，針對含分布式電源城市電網的故障分析，許多學者做了大量研究。其中主要分為兩個方面：1)考慮分布式電源的控制策略，包括PQ控制、V/f控制與下垂控制3-4，同時計及低電壓穿越特性、限流環節等；2)從分布式電源的出力入手，考慮分布式電源輸出的隨機性，反映故障潮流的真實情況。

對于第1個方面，目前已有大量的研究成果。文獻[5]在考慮逆變型分布式電源低電壓穿越特性基礎上，提出限制輸出電流與功率的控制策略。文獻[6]考慮逆變型分布式電源的PQ控制策略，將多個分布式電源進行等值，并對故障網絡分區，簡化了含多逆變型分布式電源復雜網絡的計算。文獻[7]分析PQ控制策略對短路電流的影響，提出適用于穩態以及次暫態的故障求解模型。文獻[8-9]基于V/f控制策略，建立了含分布式電源網絡的故障等值模型。上述文獻在故障分析中考慮了逆變型分布式電源的控制策略，但其出力大小受環境因素具有隨機性，使得故障時的潮流情況也是不確定的，從單一運行點計算不能確切地反應實際情況。

對于第2個方面，目前的研究工作較少，文獻[10]利用蒙特卡洛法對分布式電源輸出功率、故障點位置等進行隨機抽樣，利用故障模型計算短路電流的概率分布。蒙特卡洛法通過大量抽樣運算具有普遍性，但該文獻在計算中未考慮分布式電源的控制策略與低電壓穿越特性等。

綜合上述研究成果，考慮分布式電源出力的隨機特性以及控制策略，提出一種基于蒙特卡洛法的故障分析方法。該方法運用蒙特卡洛法對分布式電源出力的概率模型進行隨機抽樣，基于PQ控制及低電壓穿越策略的故障計算方法對故障電壓與短路電流的概率分布進行求解；最后，通過算例對所提故障分析方法進行仿真驗證。

1 分布式電源的概率模型

高比例分布式電源的并網改變了城市電網的基本特征。一方面，城市電網結構發生變化，由傳統單電源網絡發展為多電源網絡，電網潮流復雜化；另一方面，分布式電源如風力發電、光伏發電受自然因素影響出力具有隨機性。下面主要介紹風機、光伏出力的概率模型以反映其隨機性特征。

1.1 風機出力概率模型

風力發電機組的出力大小與風速有關，通常采用雙參數威布爾分布來描述風速的變化情況[11]。

(1)

式中：v為實際風速；a和b分別為雙參數威布爾分布的形狀參數與尺度參數。

風機出力與風速的關系為

(2)

式中：PW為風電機組出力；vci、vr、vco分別為風電機組的切入風速、額定風速、切出風速；PN為風電機組的額定功率。

結合式(2)可得風機出力的概率密度函數為

(3)

式中：c1=PN/(vr-vci)；c2=-c1vci。

1.2 光伏出力概率模型

據大量統計資料表明，一段時間內大部分地區的光照強度變化可近似看作服從Beta分布[12]。

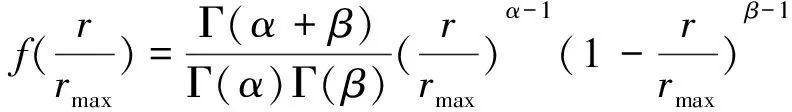
(4)

式中：r和rmax分別為這段時間內的實際光照強度與最大光照強度；Γ為伽馬函數；α和β為Beta分布的形狀參數。

光伏發電機組出力與光照強度的關系可由式(5)表示，結合式(4)可得光伏出力的概率密度函數，見式(6)。

PP=γAη

(5)

(6)

式中：PP和PPmax分別為光伏發電機組的實際出力和最大出力；A為光伏板面積；η為轉換效率。

2 基于蒙特卡洛法的含分布式電源的城市電網故障分析方法

分布式電源出力的隨機特性使得傳統基于某一運行點的故障分析方法難以滿足實際情況，同時其輸出受控制策略影響也呈現不同的故障特征。這里提出基于蒙特卡洛法的含分布式電源的城市電網故障分析方法，利用蒙特卡洛法生成服從出力分布的數據代入考慮PQ控制策略的故障計算中，解決現有方法未考慮控制策略或出力隨機性等問題。

2.1 逆變型分布式電源等值模型

分布式電源種類繁多，根據并網方式可分為旋轉型分布式電源和逆變型分布式電源(inverter interfaced distributed generation，IIDG)兩種。其中旋轉型分布式電源采用同步機并網，可直接接入電網；逆變型分布式電源則通過電力電子變流器接入電網[13]。目前城市電網中大多數分布式電源為逆變型，這里主要研究逆變型分布式電源。

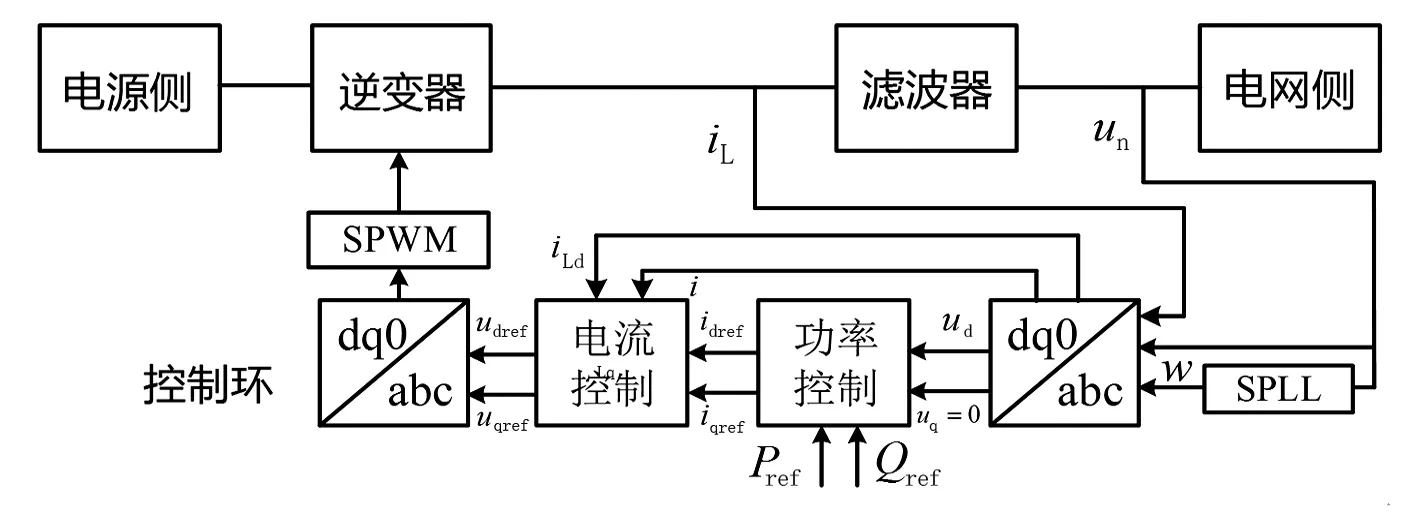
圖1 基于PQ控制策略的分布式電源并網結構

逆變型分布式電源通常采用PQ控制策略進行并網，如圖1所示。在此控制下，逆變器的輸出電流跟隨參考值發生變化，可由式(7)表示。

(7)

式中：Pref、Qref分別為有功功率參考值和無功功率參考值；idref、iqref分別為逆變器輸出的有功參考電流和無功參考電流；ud為電網側電壓的d軸分量。

城市電網正常運行時，在考慮可再生能源充分利用的基礎上，逆變型分布式電源不輸出無功功率。在電網發生故障時，逆變型分布式電源提供的故障電流與其并網點電壓和有功功率參考值有關。同時逆變型分布式電源還需具有無功支撐能力的低電壓穿越特性與限流環節[14]。為滿足該要求，分布式電源輸出電流滿足式(8)—式(10)。同時，逆變器優先輸出無功電流，以保證電網的穩定性。

(8)

(9)

(10)

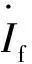
2.2 基于蒙特卡洛法的城市電網故障分析方法

對于電網的故障計算可通過節點電壓方程進行求解，而在含逆變型分布式電源的電網發生故障時，分布式電源的輸出電流與并網點電壓和有功參考值有關，則需對方程進行迭代求解[15]：

(11)

(12)

(13)

式中：Y為節點導納矩陣；k為迭代次數。

由上述計算模型可得網絡故障電壓電流值。而在計及分布式電源出力的隨機性時，可將修正方程式中的有功參考值看作服從相應的概率分布，利用蒙特卡洛法進行隨機抽樣，將生成的樣本值帶入到PQ控制策略下的故障計算模型，得到一系列電壓電

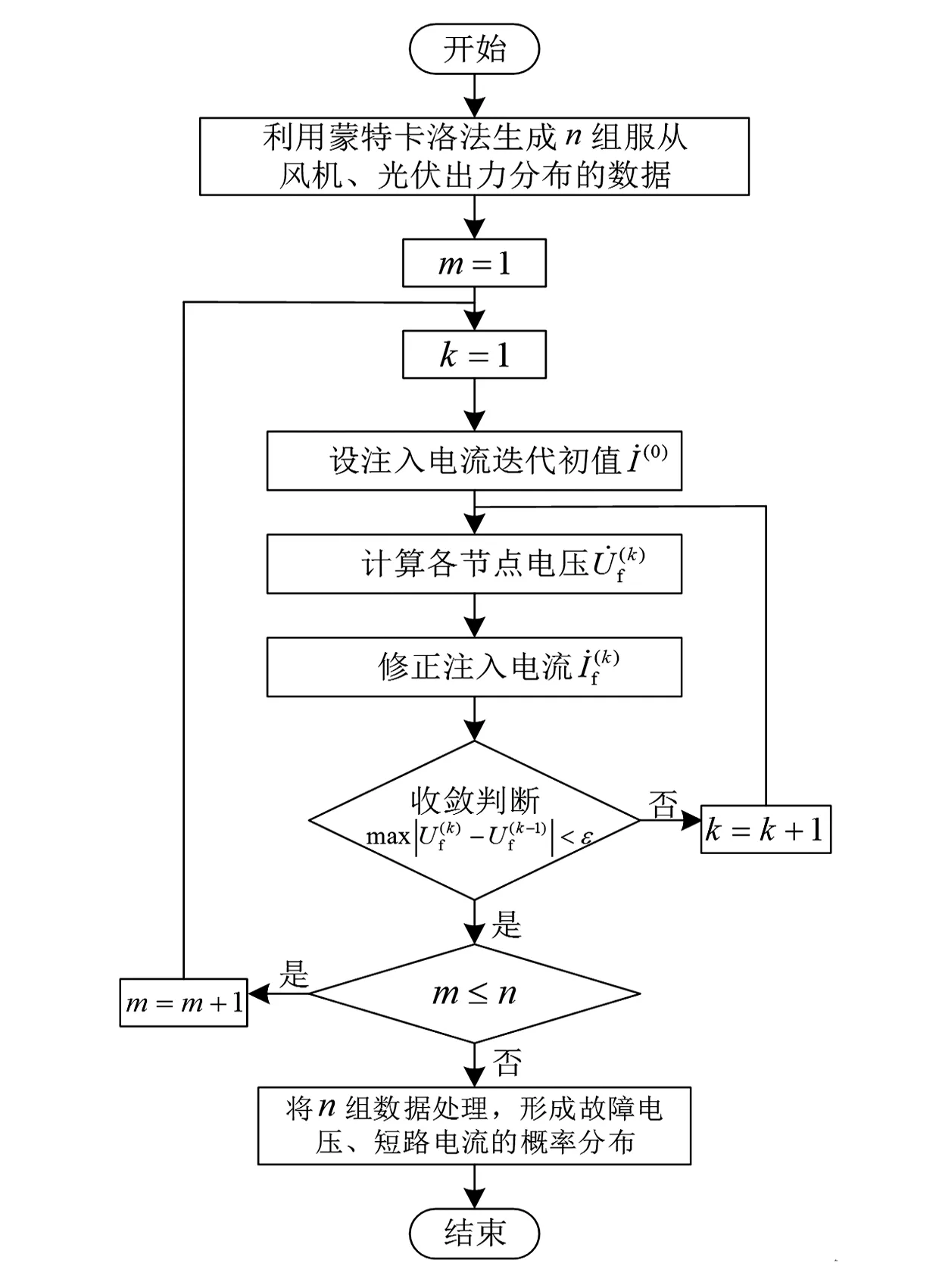
圖2 算法流程

流值，通過統計分析形成故障電壓、短路電流的概率分布。蒙特卡洛法通過大量抽樣計算來獲取系統空間的隨機狀態，不限制系統規模，適用于城市電網的計算分析。

綜上，基于蒙特卡洛法的含分布式電源的城市電網故障分析方法流程圖如圖2所示。

3 算例分析

3.1 仿真場景設定

利用所提方法進行仿真分析。如圖3所示，DG1、DG2為風電機組，DG3、DG4為光伏電站，具體參數設置如下。

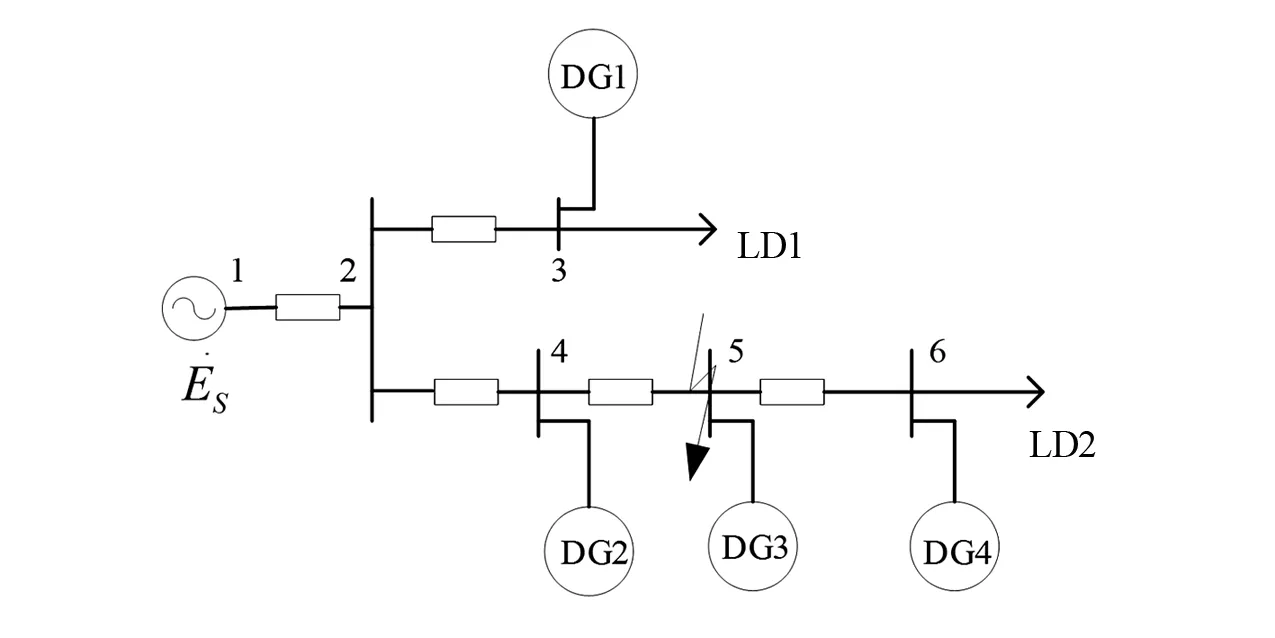
圖3 算例模型

1)風機出力滿足威布爾分布，風電機組額定功率為1 MW，切入風速、切出風速、額定風速分別為4 m/s、25 m/s、15 m/s，實際風速表見文獻[16]。

2)光伏出力滿足Beta分布，光伏電站最大光強為250 W/m2，總光伏面積為35 000 m2，轉換效率為15%，參數α、β分別為0.45、9.19[17]。

設定支路4-5末端發生三相短路，過渡電阻為1 Ω，利用所提方法對故障網絡進行分析。

3.2 基于蒙特卡洛法的故障分析方法仿真結果

通過所提方法對節點5電壓幅值和支路4-5短路電流的概率密度函數與累積分布函數曲線進行計算，結果如圖4、圖5所示。

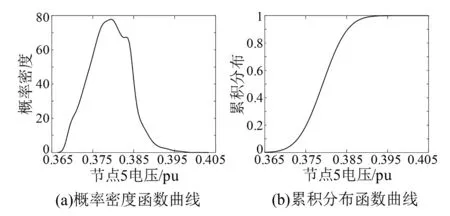
圖4 節點5電壓概率分布

由圖4、圖5可知，故障后電壓、電流具有波動性，節點5電壓范圍為0.364～0.397 pu，支路4-5短路電流范圍為4.29～4.55 pu。此電壓電流的概率分布表示在考慮風機出力呈威布爾分布、光伏出力呈Beta分布時，該網絡發生故障后，電壓電流所出現的范圍區間，不同數值出現的概率不同。可見在計及風電、光伏出力隨機性時，城市電網故障潮流也具有概率特性。

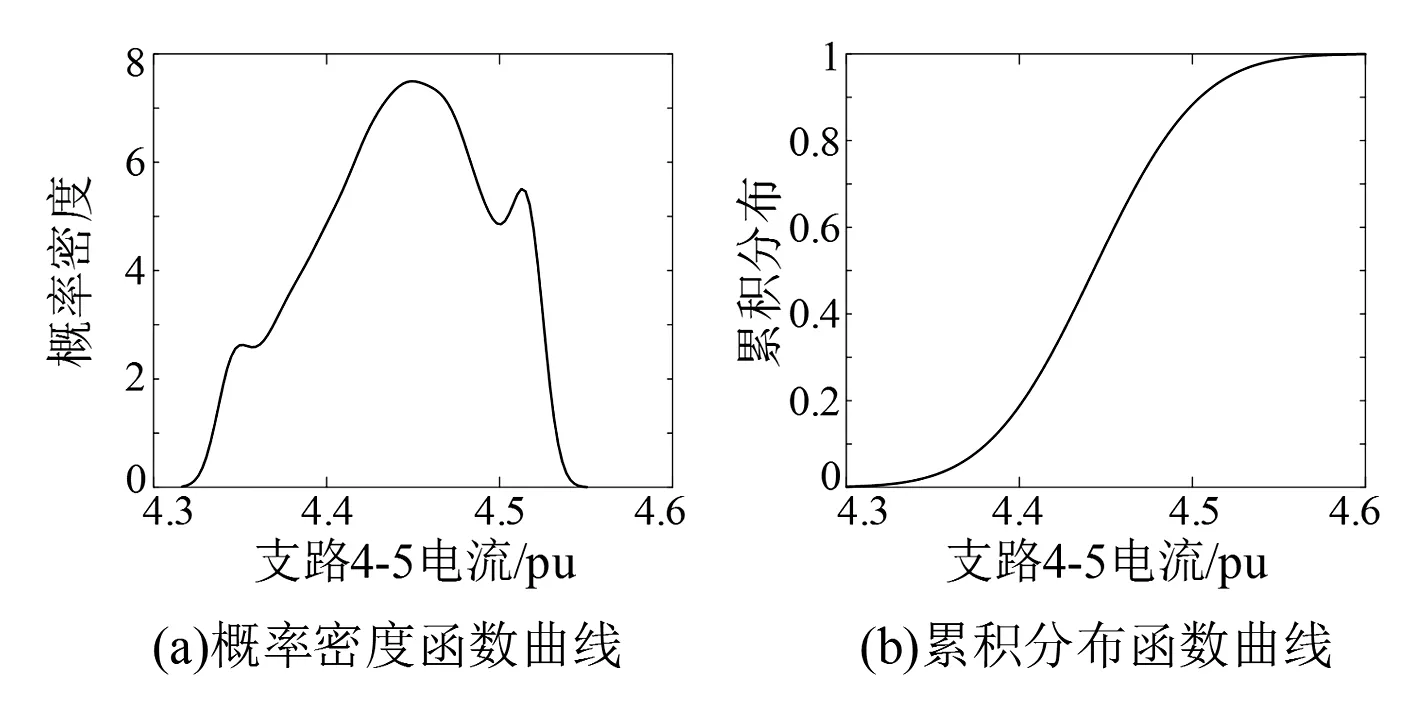
圖5 支路4-5短路電流概率分布情況

同時在圖3所示電網中，設風電機組和光伏機組出力分別為550 kW、65 kW，利用Matlab/Simulink對故障網絡進行仿真分析，以一相為例得到節點5電壓和支路4-5電流的有效值，如表1所示。

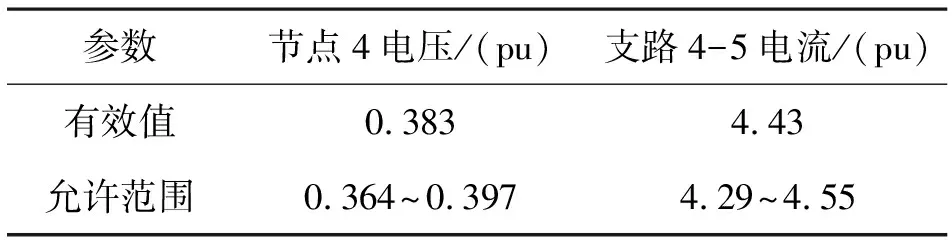
表1 仿真結果

節點4電壓與支路4-5短路電流幅值有效值分別為0.383 pu、4.43 pu，滿足在計及出力隨機性后故障電壓電流的范圍內，證明該方法可得含分布式電源的城市電網故障后電壓電流的波動區間，即該故障分析方法考慮了分布式電源出力的概率特性，而不僅以固定出力值參與計算分析，符合實際情況，可對保護整定值的設置等提供一定的參考。

4 結 語

在考慮分布式電源出力的概率特性基礎上，提出了一種基于蒙特卡洛法的含分布式電源的城市電網故障分析方法。通過理論分析與仿真驗證，得出如下結論：

1)在含逆變型分布式電源的故障計算模型中，逆變型分布式電源提供的故障電流與其有功參考值有關，可將該有功參考值看做服從出力分布進行故障分析計算。

2)所提方法考慮了分布式電源出力的隨機特性在故障分析中的影響，不以單一基準點為例，可得故障電壓與短路電流的概率分布，同時該方法利用抽樣計算，具有普遍性，對故障特性分析以及保護裝置整定值的配置具有一定的參考價值。