關(guān)于一些特殊圖上的強(qiáng)羅馬控制數(shù)的研究

徐加雪, 王志平

(大連海事大學(xué)理學(xué)院，大連 116000)

1 引言

對(duì)本文使用的符號(hào)和術(shù)語(yǔ)進(jìn)行說(shuō)明.圖G 是由頂點(diǎn)集合V(G)和邊集合E(G)構(gòu)成的一個(gè)簡(jiǎn)單圖.n = |V(G)|表示圖G 的階數(shù)，|E(G)|表示圖G 的邊數(shù).對(duì)于圖中的每一個(gè)頂點(diǎn)v ∈V(G)，它的開(kāi)鄰域和閉鄰域分別用N(v) = {u ∈V(G)|uv ∈E(G)}和N[v] =N(v)∪{v}對(duì)應(yīng)表示.d(v) = |N(v)|表示頂點(diǎn)v 的度.f 代表定義在頂點(diǎn)集合V(G)上的函數(shù).f : V(G) →{0,1,2}即表示圖中任意的頂點(diǎn)v ∈V(G), f(v) = 0 或1 或2.?=?(G)和δ =δ(G)分別表示圖G 的最大度和最小度.

圖論起源于十八世紀(jì)，是一個(gè)有著豐富歷史背景和實(shí)用價(jià)值的學(xué)科.它是由日常生活中的游戲激發(fā)產(chǎn)生的，至今已經(jīng)有兩百多年的發(fā)展歷史.上個(gè)世紀(jì)中期，Clande Berge 學(xué)者根據(jù)國(guó)際象棋問(wèn)題首先提出了圖的“控制數(shù)”的概念.受Berge 學(xué)者的啟示，Oystein Ore 學(xué)者正式提出了控制數(shù)以及相關(guān)方面的術(shù)語(yǔ)并延續(xù)至今.基于不同的實(shí)際應(yīng)用背景以及歷史背景，圖的控制數(shù)衍生出許多新的控制參數(shù)，例如弱控制數(shù)、獨(dú)立控制數(shù)、距離控制數(shù)、符號(hào)邊控制、羅馬控制數(shù)等，控制數(shù)的種類(lèi)不斷增加.

Stewart 在文獻(xiàn)[1]中講述了公元四世紀(jì)時(shí)羅馬帝國(guó)的君主保衛(wèi)國(guó)家的故事.我們把整個(gè)羅馬帝國(guó)視為一個(gè)圖，令圖中的點(diǎn)表示羅馬帝國(guó)中的每個(gè)地區(qū)，邊表示兩個(gè)地區(qū)相鄰.沒(méi)有軍隊(duì)駐扎的地區(qū)稱(chēng)為不安全的地區(qū)，反之則稱(chēng)其為安全的地區(qū).軍隊(duì)需要駐扎在不同的地區(qū)守護(hù)國(guó)家的領(lǐng)土安全.安全系數(shù)最高的方案是在羅馬帝國(guó)內(nèi)的每一個(gè)地區(qū)都駐扎一支軍隊(duì).若國(guó)家長(zhǎng)期處于和平時(shí)期，這種防御方案便會(huì)造成軍隊(duì)資源的浪費(fèi).君主希望在羅馬帝國(guó)內(nèi)的每個(gè)地區(qū)駐扎數(shù)量較少的軍隊(duì)，同時(shí)能夠維持國(guó)家的領(lǐng)土完整與安全，于是頒布了一條法令：從一個(gè)安全的地區(qū)派遣軍隊(duì)去往一個(gè)不安全的地區(qū)后，使安全的地區(qū)轉(zhuǎn)變?yōu)椴话踩貐^(qū)的情況不可以存在.根據(jù)君主的命令可知，只有至少駐扎兩個(gè)軍隊(duì)的安全地區(qū)才能夠往相鄰的不安全的地區(qū)派遣軍隊(duì)，這樣既能夠保證安全地區(qū)在派遣軍隊(duì)之后仍是安全的地區(qū)，相鄰的不安全的地區(qū)接收派遣的軍隊(duì)后也轉(zhuǎn)變?yōu)榘踩貐^(qū).在總結(jié)已有經(jīng)驗(yàn)的基礎(chǔ)上，1999 年，Stewart 首次提出了羅馬控制概念[1].Cockayne 等學(xué)者[2]受保衛(wèi)羅馬帝國(guó)的歷史故事的啟發(fā)，正式給出了圖G 的頂點(diǎn)集合上的羅馬控制函數(shù)的定義，如下所示：

實(shí)際生活中，敵人更傾向于攻擊薄弱的地區(qū).當(dāng)羅馬帝國(guó)的地區(qū)面臨敵人的多重攻擊時(shí)，駐扎兩個(gè)軍隊(duì)的安全地區(qū)，無(wú)法保護(hù)數(shù)量超過(guò)三個(gè)以上的不安全的鄰居，此時(shí)羅馬帝國(guó)很容易失守而落入敵人手中.于是Alvarezruiz 等學(xué)者[17]提出一種更符合實(shí)際情況的防御新策略，并且定義了圖G 的強(qiáng)羅馬控制函數(shù)，具體地，

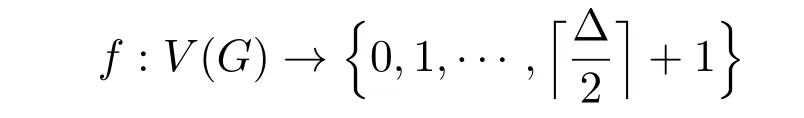
是一個(gè)定義在圖G 的頂點(diǎn)集合V(G)上的函數(shù)，若每一個(gè)頂點(diǎn)v ∈B0至少存在一個(gè)鄰結(jié)點(diǎn)w ∈B2，且鄰結(jié)點(diǎn)w 滿(mǎn)足

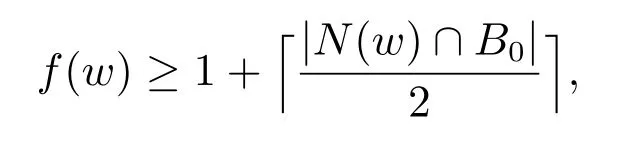
其中

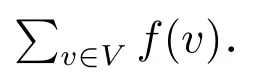
圖1 和圖2 分別給出了圖G 上的羅馬控制函數(shù)和強(qiáng)羅馬控制函數(shù).一次大地震過(guò)后往往會(huì)伴隨著許多余震的發(fā)生，數(shù)量有限的軍隊(duì)需要駐扎在災(zāi)區(qū)，隨時(shí)準(zhǔn)備營(yíng)救受災(zāi)群眾.假設(shè)村莊用圖中的點(diǎn)表示，村莊之間的路用圖中的邊表示.圖上的數(shù)字表示該村莊中駐扎軍隊(duì)的數(shù)量.當(dāng)面臨多個(gè)村莊都需要營(yíng)救時(shí)，圖1 中的軍隊(duì)不能夠及時(shí)營(yíng)救它周?chē)惺転?zāi)的村莊，但圖2 中的軍隊(duì)至少能夠及時(shí)營(yíng)救一半以上沒(méi)有軍隊(duì)駐扎的村莊，大大減少生命財(cái)產(chǎn)損失.

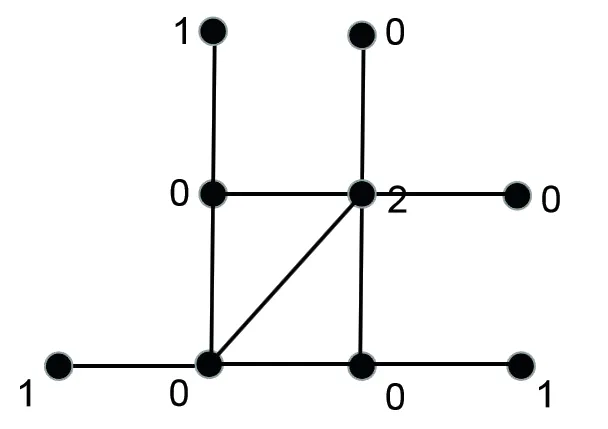
圖1: 圖G 的羅馬控制函數(shù)

圖2: 圖G 的強(qiáng)羅馬控制函數(shù)

人們往往希望利用一個(gè)多項(xiàng)式時(shí)間算法來(lái)求出所有圖上的控制數(shù)的精確值，但已有結(jié)論指出一般圖的控制問(wèn)題是一個(gè)NP-完備問(wèn)題，因此探究出圖的控制數(shù)或者控制數(shù)較好的上下界具有重大的理論意義.Alvarezruiz 等學(xué)者在文獻(xiàn)[17]中提出了一個(gè)開(kāi)放性問(wèn)題：所有階為n ≥3 的連通圖是否都有γStR(G)≤成立.為了驗(yàn)證問(wèn)題的正確性，本文應(yīng)用數(shù)學(xué)歸納法和分類(lèi)討論方法，深入地討論了圖的強(qiáng)羅馬控制數(shù)與階數(shù)的關(guān)系，得到了風(fēng)車(chē)圖、完全二部圖、完全圖的刺圖等特殊圖上的強(qiáng)羅馬控制數(shù)均不大于其階數(shù)的七分之六，從而進(jìn)一步說(shuō)明了問(wèn)題的正確性.

2 主要結(jié)論與證明

定理1若G 是一個(gè)階為n ≥3，最大度為?=n ?1 的圖，則γStR(G)≤.

證明 假設(shè)圖G 中的頂點(diǎn)v ∈V(G)的度為d(v) = ?= n ?1.在圖G 的頂點(diǎn)集V(G)上定義一個(gè)函數(shù)f :V(G)→{0,1,··· ,+1}，令f(v)=+1，而對(duì)任意的頂點(diǎn)x ∈N(v)，都有f(x) = 0.顯然，函數(shù)f 是圖G 的頂點(diǎn)集V(G)上一個(gè)強(qiáng)羅馬控制函數(shù)，因此

同理可知，風(fēng)車(chē)圖、扇圖、鳳梨圖等都是階為n ≥3 且最大度為?=n ?1 的圖，所以這些特殊圖均滿(mǎn)足γStR(G)≤.

若圖G 的頂點(diǎn)集合V(G)劃分為兩個(gè)頂點(diǎn)子集V1、V2，且滿(mǎn)足在同一頂點(diǎn)子集的任意兩個(gè)頂點(diǎn)之間不存在邊且圖中的每條邊連接不同頂點(diǎn)子集中的頂點(diǎn)，則稱(chēng)圖G 是一個(gè)二部圖. 若圖G 是一個(gè)二部圖，且頂點(diǎn)子集V1中的任意一個(gè)頂點(diǎn)均鄰接頂點(diǎn)子集V2中所有的頂點(diǎn)，此時(shí)則稱(chēng)圖G 為完全二部圖，如圖3 所示.

圖3: 完全二部圖

定理2若圖G 是一個(gè)階為n ≥3 的完全二部圖，則γStR(G)≤.

證明 令|V1|=p, |V2|=q 且p ≥q.根據(jù)假設(shè)可知?=p 和n=p+q.下面分4 種情形來(lái)討論.

情形1n=3.

顯然有p=2, q =1 且?=2.根據(jù)定理1 可知γStR(G)≤成立.

情形2n=4.

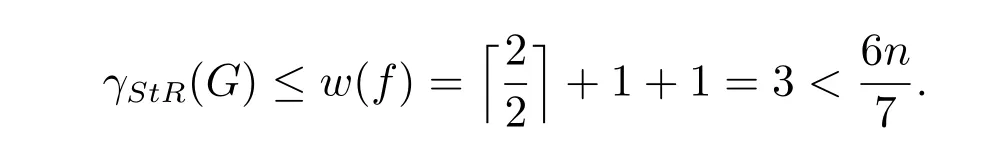
情形2.2 當(dāng)p = 3, q = 1 時(shí)，則?= 3 = n ?1，由定理1 可知γStR(G) ≤成立.

情形3n=5.

情形3.1 當(dāng)p = 3, q = 2 時(shí)，則?= 3.假設(shè)頂點(diǎn)v ∈V2是圖G 中度數(shù)最大的頂點(diǎn)，即d(v) = ?(G).在圖G 的頂點(diǎn)集合V(G)上定義一個(gè)函數(shù)f : V(G) →{0,1,··· ,+ 1}，令f(v) =+ 1，而對(duì)所有與頂點(diǎn)v 鄰接的頂點(diǎn)x ∈N(v)，都有f(x) = 0，剩余結(jié)點(diǎn)f(w) = 1.顯然，函數(shù)f 是圖G 的頂點(diǎn)集合V(G)上的一個(gè)強(qiáng)羅馬控制函數(shù)，因此有

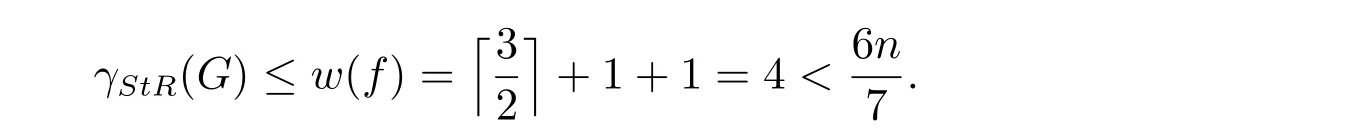
情形3.2 當(dāng)p = 4, q = 1，此時(shí)?= 4 = n ?1.根據(jù)定理1 可知γStR(G) ≤成立.

情形4n ≥6.

在圖G 的頂點(diǎn)集合V(G)上定義一個(gè)函數(shù)f :V(G)→{0,1,··· ,+1}，令

其中v1∈V1, v2∈V2，剩余結(jié)點(diǎn)f(w) = 0.函數(shù)f 是圖G 頂點(diǎn)集合V(G)上的一個(gè)強(qiáng)羅馬控制函數(shù)，因此有

假設(shè)Kz是一個(gè)z 階完全圖，a1,a2,··· ,az是正整數(shù)且a1≥a2≥···≥az≥1.通過(guò)在完全圖的每個(gè)頂點(diǎn)處分別添加a1,a2,··· ,az個(gè)懸掛邊可得到完全圖的刺圖，記做.我們對(duì)圖中的結(jié)點(diǎn)進(jìn)行標(biāo)記，圖4 展示了完全圖K3的刺圖的頂點(diǎn)標(biāo)記規(guī)則.

圖4: 完全圖K3 的刺圖

定理3若是一個(gè)階n ≥3 的完全圖Kz的刺圖，則γStR()≤.

情形1a1=a2=···=az=1.

在這種情形下，圖K?z的階和最大度分別對(duì)應(yīng)為n = 2z 和?= z.在圖的頂點(diǎn)集合V()上定義一個(gè)函數(shù)f :V()→{0,1,··· ,+1}，選取圖中任意一個(gè)非葉子頂點(diǎn)v ∈V(K)，令f(v) =+1，而對(duì)所有與頂點(diǎn)v 相鄰接的頂點(diǎn)x ∈N(v)，有f(x) = 0，使得剩余結(jié)點(diǎn)均滿(mǎn)足f(w) = 1.根據(jù)強(qiáng)羅馬控制函數(shù)函數(shù)的定義可知，函數(shù)f 是圖的頂點(diǎn)集合V()上的一個(gè)強(qiáng)羅馬控制函數(shù)，因此有

情形2ai≥2，其中i=1,2,··· ,z.

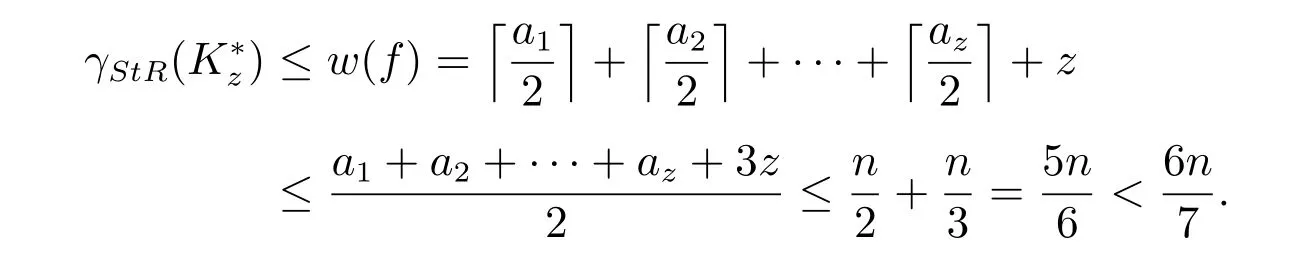
情形3a1=a2=···=ak=2, ak+1=···=az=1，其中1 ≤k ≤z ?1.

假設(shè)頂點(diǎn)v1鄰接兩個(gè)懸掛邊.在圖K?z的頂點(diǎn)集合V(K?z)上定義一個(gè)函數(shù)f :V() →{0,1,··· ,+ 1}，令f(v1) =+ 1，而對(duì)所有與頂點(diǎn)v1相鄰接的頂點(diǎn)x ∈N(v1)，均有f(x) = 0，其他剩余結(jié)點(diǎn)f(w) = 1.顯而易見(jiàn)，f 是圖K?z的一個(gè)強(qiáng)羅馬控制函數(shù)，因此有

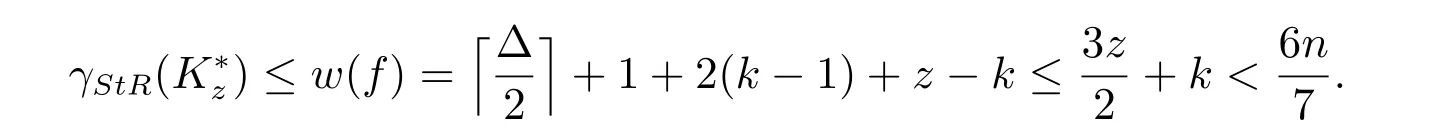
情形4a1≥3, a2≥3, ··· , ak≥3, ak+1=···=az=1，其中2 ≤k ≤z ?1.

情形4.1 當(dāng)2 ≤k ≤3 時(shí)，在圖的頂點(diǎn)集合V()上定義一個(gè)函數(shù)f :V()→{0,1,··· ,+1}，令f(v1)=+1，而對(duì)所有與頂點(diǎn)v1相鄰接的頂點(diǎn)x ∈N(v1)，均有f(x) = 0，剩余結(jié)點(diǎn)f(w) = 1.函數(shù)f 是圖頂點(diǎn)集合V()上的一個(gè)強(qiáng)羅馬控制函數(shù)，因此有

因?yàn)?/p>

情形4.2 當(dāng)4 ≤k ≤z ?1 時(shí)，在圖Kz?的頂點(diǎn)集合V(Kz?)上定義一個(gè)函數(shù)f :V()→{0,1,··· ,+1}，令

對(duì)所有x ∈N(v1)∪N(v2)∪···∪N(vk)?{v1,v2,··· ,vk}，均有f(x)=0，其他剩余結(jié)點(diǎn)f(w)=1.顯然，函數(shù)f 是圖K?z頂點(diǎn)集合V(K?z)上的一個(gè)強(qiáng)羅馬控制函數(shù)，因此有

因?yàn)?/p>