高速公路機電設備使用壽命評估方法研究

周曉旭

（山西省交通科技研發有限公司，山西 太原 030032）

0 引言

我國公路建設發展迅速，公路里程持續增長，截至2018年底，全國高速公路里程達到14萬km，公路路網布局日趨合理，公路技術等級和路面等級進一步提高，公路機電設備也日益完善，同時，機電設備在高速公路通車后運營管理過程中的作用也日益顯著。高速公路機電設備數量龐大、種類繁多，其運行的安全性和可靠性不僅影響了高速公路日常運營質量和安全效益，更重要的是影響到公眾出行和交通的有序運轉[1]。

目前，對于高速公路設備的健康狀況和養護質量研究更多側重于設備的故障率和經濟壽命，通過開展維修維護的策略研究和折舊分析，確定機電設備經濟的報廢平衡點和維修方案[2-3]。而在高速公路實際運營和養護管理過程中，機電設備更多是基于故障、實際使用壽命等開展管養活動，檢修、更新、報廢等往往通過主觀判斷，養護主要圍繞經常性故障的機電設備開展，缺乏數據支撐和科學規劃，經濟型和合理性欠妥。因此，準確預測機電設備使用壽命不僅能夠為科學管養提供數據依據，還能夠保障機電設備安全運行，有效避免機電設備故障造成損失，對于高速公路正常有序的運營具有十分重要的意義。

本文以高速公路機電設備使用壽命為研究對象，針對高速公路機電設備使用壽命數據不準和缺少科學計算方法的現狀，基于統計學和可靠性的理論，提出一種高速公路機電設備使用壽命預測方法，并以某高速公路收費站攝像機為例，通過擬合AD分布檢驗、極大似然估計等方法，構建攝像機機電設備故障壽命分布模型，進一步通過K-S檢驗該數學進行交叉驗證，驗證本文提出的壽命預測方法的可行性和準確性，并計算出攝像機平均壽命、可靠度和可靠壽命、檢修周期等壽命評定指標，基本與收費站攝像機實際經驗一致。本方法的提出可為高速公路機電設備的日常檢修、更新和報廢提供決策依據，降本增效。

1 壽命預測方法研究

1.1 理論基礎

機電設備從投入使用到失效的一段時間稱為壽命，由于機電設備的失效是隨機的，故其壽命不是定值而是隨機變量，在工程實踐中通常使用概率分布來描述這些隨機變量的分布特性。常用描述壽命分布的模型主要有Weibull分布模型、指數分布模型、正態分布模型和極值分布模型等。通常，一個較復雜的機電系統（或設備），在穩定工作時期的偶然失效時間隨機變量一般服從指數分布；在損耗期失效服從正態分布；機電設備的疲勞往往呈現對數正態分布或 Weibull分布[4-5]。

1.1.1 Weibull分布模型

三參數Weibull分布的故障概率密度函數和故障壽命分布函數：

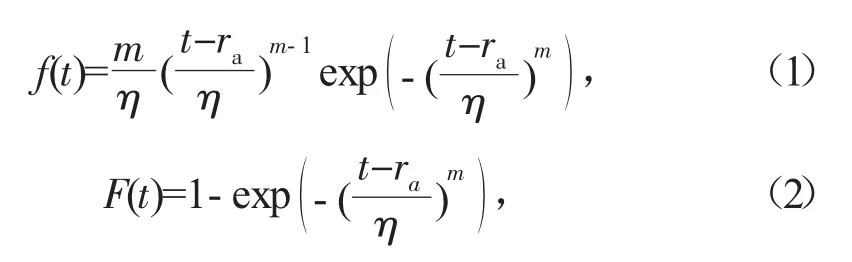
式中：m為尺度參數；η為形狀參數；ra為位置參數；t為時間；當 ra為 0時，式（1）、式（2）為兩參數 Weibull分布。

1.1.2 指數分布模型

指數分布的故障概率密度函數和故障壽命分布函數：

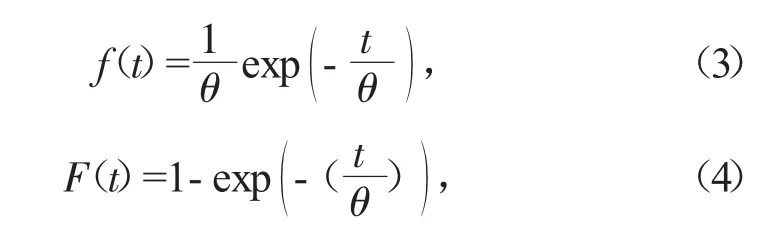
式中：θ為尺度參數；t為時間。

1.1.3 正態分布模型

正態分布的故障概率密度函數和故障壽命分布函數：

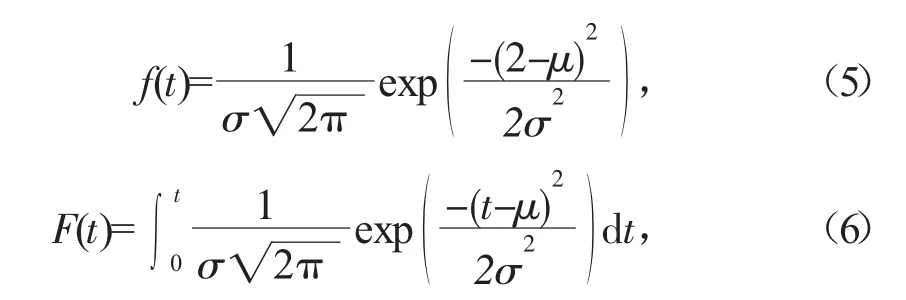
式中：μ為均值；σ為方差。

1.2 數據擬合和分布檢驗

1.2.1 擬合AD分布檢驗

擬合AD分布檢驗是統計學中通過數據擬合的方式檢驗所收集的數據是否服從某個分布的非參數檢驗方法，通過計算Anderson-Darling統計量（AD統計量）和p值判斷是否符合某目標分布，如式（7）所示。AD統計量其實質是概率圖中點離擬合直線距離大小的加權平方和，越靠近分布的尾部，權重越大；AD統計量越小數據分布就越接近目標分布；越大則服從目標分布的可能性就越小。根據AD統計量計算擬合優度檢驗的p值，如果p值大于0.05，則數據服從目標分布，如果p值小于0.05，則數據不服從目標分布。

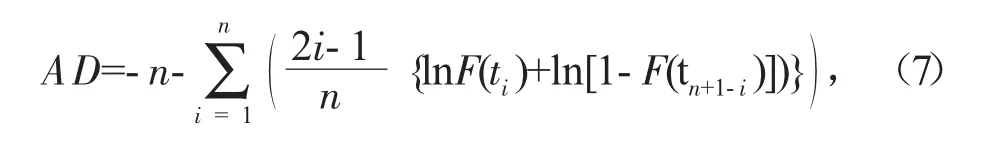
式中：AD為AD統計量；i為樣本格式；F(ti)為累計故障分布函數；n為樣本總量。

1.2.2 參數估計

根據擬合優度分布檢驗確定最優的故障壽命分布模型，通過參數估計來確定故障壽命分布模型的參數。常用的參數估計方法有矩法估計、最小二乘估計、極大似然估計、貝葉斯估計等，由于高速公路壽命數據通常為不完全樣本，需要通過故障壽命分布函數來推斷總體故障分布情況。極大似然估計是一種通過似然函數獲得總體參數估計的方法，其結果具有無偏性、有效性和相合性等優良性質，被廣泛采用，本文選用極大似然估計來進行參數估計。

設總體X=x的概率密度為f（x：θ），其中θ是待估計參數，那么當樣本值為x1，x2…xn時，有：

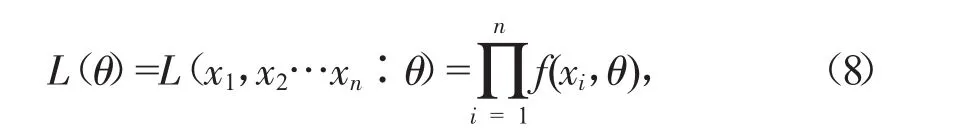
式中：L(θ)稱為樣本的似然函數。

若滿足

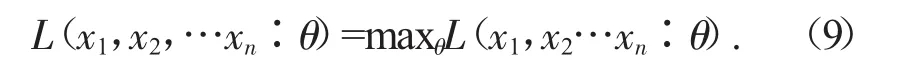
當參數θ=θ*時，似然函數取最大值，那么θ*就叫做參數θ的極大似然估計值。求解似然方程，令：

即可求出θ*值，式中，i為未知參數θ的個數。

1.2.3 檢驗驗證

假設檢驗主要是用來驗證通過參數估計確定的壽命分布函數是否符合真實性。常用的檢驗方法有K-S檢驗和卡方檢驗（X2檢驗），兩種方法都能用來檢驗一組樣本數據的觀測經驗分布是否與某一已知的理論分布相符合，但X2檢驗過程受樣本數量限制，需要大量樣本數據；而對K-S檢驗不受樣本數量限制，也適用于樣本數量較少的情況，且該方法對數據的分布類型判定更為敏感，檢測效果更佳，在實際中應用較多，本文采用K-S檢驗來完成對數據的檢驗驗證。

對于給定的樣本空間，設樣本容量為n，將觀測數據按從小到大的順序重新排列，構造累計頻數分布函數Sn(x)：

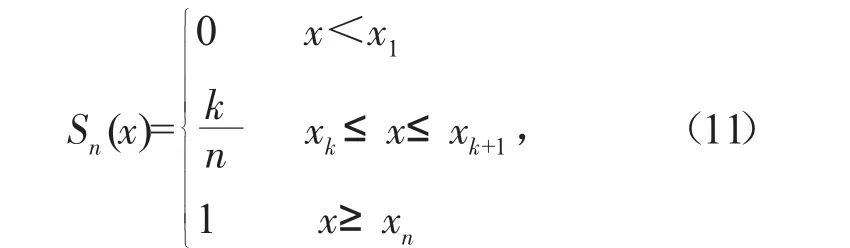
式中：x1，x2…xn為排列后的樣本數據；Sn(x)為構造的累計頻率函數。

將理論分布累計頻數分布函數F(x)，構建K-S檢驗統計量Dn：

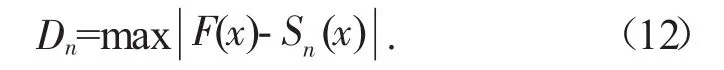
在一定的空間樣本n和顯著水平α下，通過檢驗統計量表確定檢驗統計量臨界值Dn*，如果Dn小于Dn*，兩個分布函數一致；如果Dn大于Dn*，兩個分布函數不同。

1.3 壽命評定指標

高速公路機電設備的壽命評定就是要確定機電設備的平均壽命、可靠度、可靠壽命和更換周期等指標，為機電設備的檢修、更新和報廢等提供技術依據。

1.3.1 平均壽命

平均壽命是機電設備壽命的平均值或數學期望，主要指機電設備平均能工作多長時間的量。對于高速公路機電設備主要是指平均故障前時間MTTF。

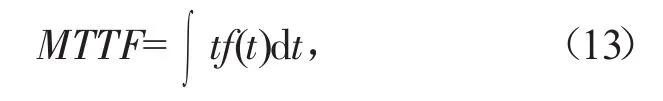
式中：f(t)為故障概率時間分布函數。

1.3.2 可靠度

可靠度是指機電設備平均無故障時間概率。

式中：F(t)為故障壽命分布函數。

1.3.3 可靠壽命

可靠壽命是指機電設備在指定可靠度下所對應的時間，其表達式為：

式中：tR0為可靠壽命；R0為指定可靠度，通常為0.95。

2 應用案例

2.1 壽命預測方法

首先，對機電設備壽命故障數據進行可靠性數據分析和處理，繪制無故障壽命頻數分布直方圖判斷分布是否符合正態分布指數分布、Weibull分布的圖形特征；運用Anderson-Darling擬合優度分布檢驗，計算壽命故障數據與不同壽命分布模型AD統計值和p值，確定與故障數據分布一致的最優故障壽命分布模型；基于極大似然估計法計算故障壽命分布模型對應未知參數，具體為指數分布的參數λ、正態分布的均值μ和標準差σ，Weibull分布的為尺度參數η、形狀參數m、位置參數ra；最后通過K-S檢驗對壽命分布進行交叉檢驗，驗證模型的正確性；并進一步計算各項壽命評定的指標來指導高速公路機電設備壽命評估。

2.2 案例分析

2.2.1 故障數據的處理和分析

本文采用機電設備故障數據為某高速公路5個收費站攝像機日常的養護故障記錄，記錄時間是從2013年1月至2017年3月，具體攝像機無故障間隔時間的數據統計如表1所示，其中，攝像機無故障間隔時間為攝像機相鄰兩次故障記錄的時間差，并對無故障間隔時間從小到大按升序排列。圖1為攝像機無故障數據間隔以N=400 d繪制無故障壽命頻數分布直方圖，對直方圖進行觀察，可以得出攝像機無故障壽命頻數分布左側分散，右側分布集中，基本符合正態分布、指數分布、Weibull分布的特征。

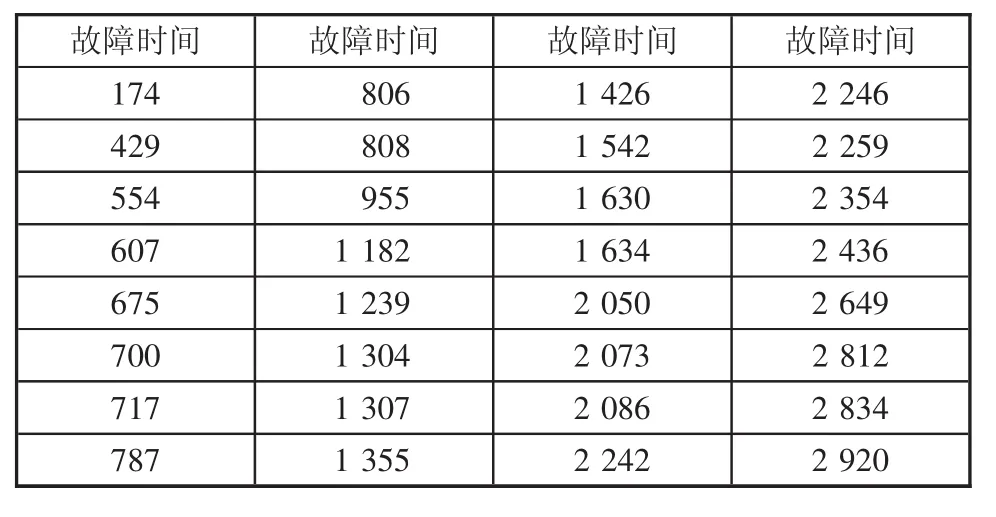
表1 某高速公路收費站攝像機無故障間隔時間統計表 d

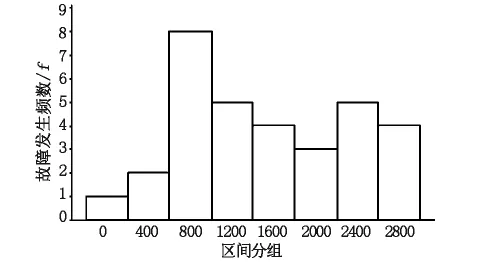
圖1 攝像機無故障壽命頻數分布直方圖

2.2.2 擬合優度分布檢驗

根據式（7）分別對攝像機無故障壽命數據進行正態分布、指數分布、2參數Weibull分布和3參數Weibull分布理論模型的分布擬合，并計算各類分布的AD統計量和p值。表1為AD統計量和p值的計算結果，圖2所示為4種分布模型擬合結果的分布概率圖。

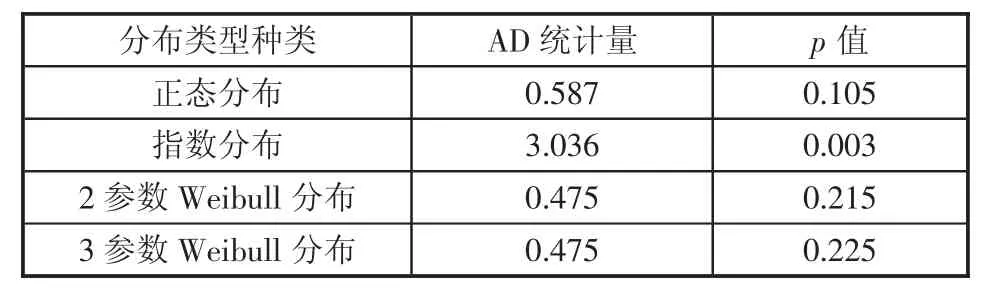
表2 不同擬合優度分布檢驗AD統計量和P值計算結果

根據圖2，攝像機故障很好地落入正態分布、2參數和3參數Weibull分布的源數據擬合區間95%的置信區間；根據表2，2參數和3參數Weibull分布的AD統計量值最小且相等為0.475，而3參數Weibull較2參數Weibull分布的p值大，且都大于顯著水平0.05，表明高速公路攝像機故障壽命數據符合2種Weibull分布模型，且3參數Weibull分布模型更優。

2.2.3 參數估計與壽命分布函數確定

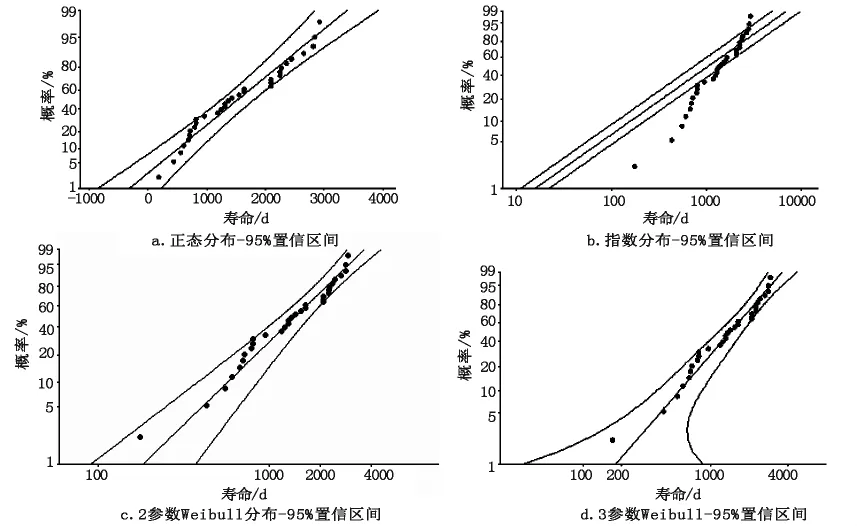
圖2 某高速公路攝像機故障數據不同分布模型擬合壽命概率分布圖

根據式（8）對高速公路攝像機的故障分布函數進行最大似然估計，計算得到3參數Weibull分布的尺度參數m=1714.9，形狀參數η=2.033，位置參數ra=5.88。根據式（2）和式（10），可得攝像機故障分布函數及可靠度函數，如式（16）和式（17）所示，圖3為攝像機壽命可靠度函數曲線。

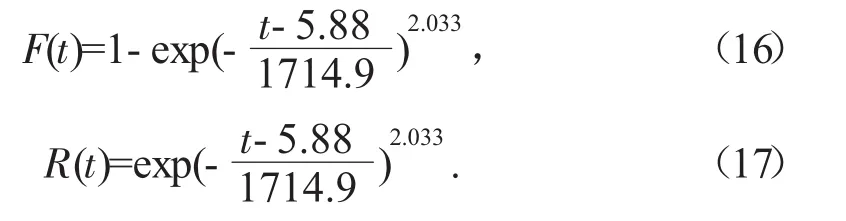
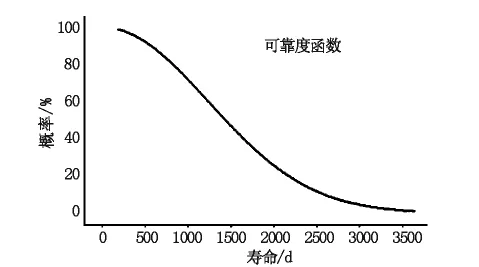
圖3 某高速公路攝像機壽命可靠度函數曲線圖

2.2.4 檢驗驗證

將某高速公路攝像機無故障壽命間隔數據按300 d間隔進行分組，并對已確定的3參數Weibull分布模型進行K-S檢驗，檢驗計算過程如表3所示。

根據表3，K-S檢驗的統計量觀察值Dn絕對值最大值為0.078，在置信水平0.05時，經查表Dn(32，0.05)=0.234＞0.078，進一步驗證了本文提出 3 參數Weibull壽命分布模型的正確性。

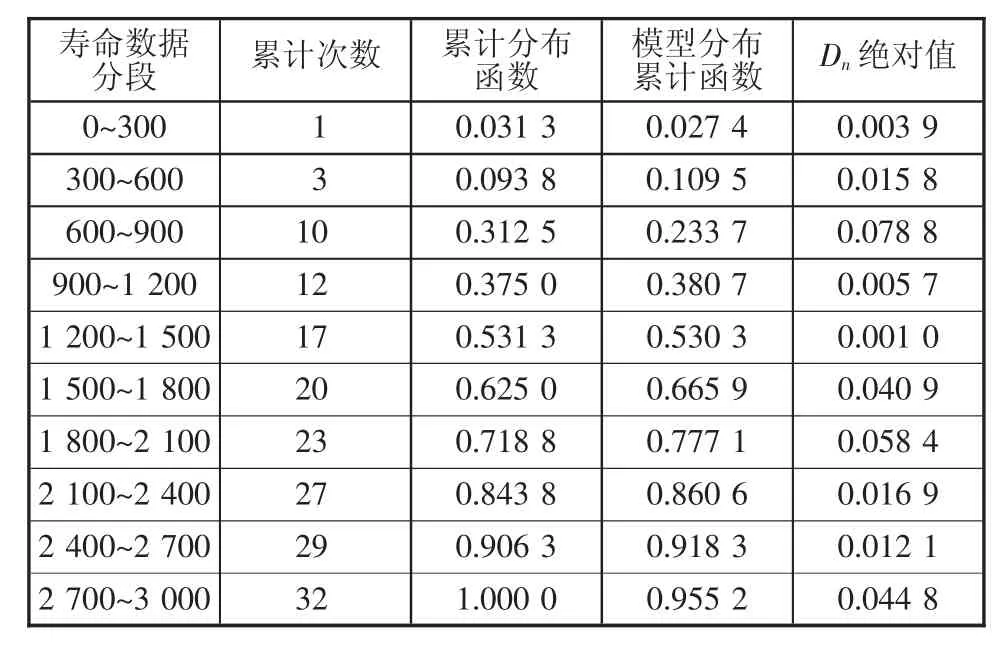
表3 某高速公路攝像機故障壽命分布模型K-S檢驗計算結果

2.2.5 可靠性評定

根據已確定的3參數Weibull故障壽命分布模型，經式（13）和式（15）計算推導，可得某高速公路攝像機平均壽命和可靠壽命計算公式為：

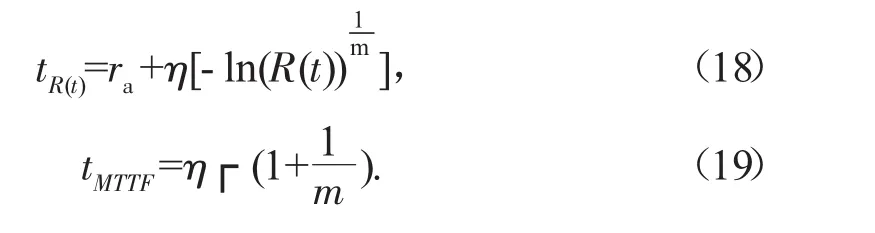
將 η=1717.2，m=2.033 代入式（18）、式（19）在可靠度為0.95情況下，某高速公路攝像機可靠壽命為398.4 d，平均壽命為1 526 d，基本與收費站攝像機實際經驗一致。因此，建議每隔0.1tMTTF（153 d）對某高速公路攝像機開展日常檢修和維護，每隔398 d在日常點檢的基礎上對攝像機開展專業檢修和狀態檢測，每隔1 526 d對攝像機進行報廢和更新計劃的提報。

3 結論

本文從高速公路機電設施運營期養護管理需求出發，針對高速公路機電設備使用壽命數據不準和缺少科學計算方法的現狀，提出了一種基于統計學和可靠性的高速公路機電設備壽命預測方法，并以某高速收費站攝像機故障壽命測算為例，通過攝像機日常養護故障數據，建立了符合數據分布特征的壽命分布預測模型，進一步計算出平均壽命、可靠度和可靠壽命、檢修周期等壽命評定指標，基本與收費站攝像機實際經驗一致。本方法的提出，可為高速公路機電設備的日常檢修、更新和報廢提供決策依據，降本增效。