王穎 程緒鐸 高夢瑤

[摘要]本文應(yīng)用修正劍橋模型和有限元方法計算平底筒倉中小麥堆的應(yīng)力分布，計算結(jié)果表明：在同一離倉軸徑向距離下，筒倉中小麥塊的豎直壓應(yīng)力隨著糧層深度的增加而增加，但接近倉底與倉壁拐角處反而減小;筒倉中小麥堆的側(cè)向壓應(yīng)力隨著糧層深度的增加而增加，但接近倉底中心反而先減小再增加。在同一深度下，筒倉中小麥堆的豎直壓應(yīng)力隨著糧塊離倉軸徑向距離的增加而減小;筒倉中小麥堆的側(cè)向壓應(yīng)力隨著糧塊離倉軸徑向距離的增加而減小，但是接近倉底處反而增加;筒倉中小麥堆的分層平均豎直壓應(yīng)力與側(cè)向壓應(yīng)力隨糧層深度的增加而增加。筒倉中小麥堆的分層平均側(cè)向壓應(yīng)力與含水率呈負相關(guān)，而小麥堆的分層平均豎直壓應(yīng)力與含水率不相關(guān)。

[關(guān)鍵詞]筒倉;小麥堆;應(yīng)力分布;修正劍橋模型;有限元方法

中圖分類號：S512.1 文獻標(biāo)識碼：A DOI：10.16465/j.gste.cn431252ts.202001

小麥儲藏在筒倉中承受著重力、摩擦力、倉壁的抵抗力，這些力的作用導(dǎo)致筒倉內(nèi)小麥堆應(yīng)力的非均勻分布[1]。筒倉中儲糧的應(yīng)力分布計算精度直接關(guān)系到糧倉的安全性和經(jīng)濟效益。

Janssen[2]提出了一種經(jīng)典理論，用于預(yù)測筒倉內(nèi)儲料的應(yīng)力分布。該理論提出了用微層平衡原理計算筒倉中儲料的垂直壓應(yīng)力和水平壓應(yīng)力的公式。但是在Janssen理論中，假設(shè)體積密度是恒定的，這導(dǎo)致了對儲料應(yīng)力值的低估[3-4]。20世紀(jì)后期，隨著計算機技術(shù)的發(fā)展，有限元法越來越多地被國際上許多學(xué)者應(yīng)用于筒倉中顆粒材料的應(yīng)力分布研究[5-7]。例如，Jofriet J C等[8]采用線彈性模型和有限元方法研究了筒倉中儲料的應(yīng)力分布;Mahmoud A等[9]采用非線性雙曲型本構(gòu)方程和有限元方法，估算了彈性波紋板的圓形筒倉壁的靜壓力;Bishara A G等[10]應(yīng)用非線性彈性模型和有限元方法估計了混凝土筒倉壁的靜壓力。

上述研究者采用的本構(gòu)方程假設(shè)材料的體積變化很小，體積變化發(fā)生在彈性變形階段，形狀變化主要發(fā)生在塑性變形階段，在塑性變形階段不發(fā)生體積變化。然而，小麥與土壤、砂土或工業(yè)材料的力學(xué)性能有很大差異，小麥籽粒松軟，小麥堆孔隙很大。因為小麥在壓應(yīng)力作用下的體積變化（縮小）很大，體積變化既發(fā)生在彈性變形階段，又發(fā)生在塑性變形階段，所以應(yīng)用上述本構(gòu)方程難以精確計算小麥在筒倉中的應(yīng)力應(yīng)變分布。相關(guān)研究人員于1968年提出了修正劍橋模型。修正劍橋模型中給出了材料的應(yīng)力增量（平均正應(yīng)力增量和廣義剪應(yīng)力增量）與塑性應(yīng)變增量（塑性體積應(yīng)變增量、塑性剪應(yīng)變增量）之間的關(guān)系，考慮了材料屈服的塑性體積變化，在土力學(xué)中得到了廣泛的應(yīng)用。由于小麥體積變化較土壤更為明顯，因此修正劍橋模型更適合于研究小麥的應(yīng)力應(yīng)變分布。本文采用修正劍橋模型和有限元方法，使用ABAQUS軟件計算平底筒倉中小麥堆的應(yīng)力分布。

1 材料與方法

1.1 實驗材料

試驗用的小麥：煙農(nóng)19號，蘇州生產(chǎn)。手工剔除破碎、不成熟的顆粒。初始含水率為12.66% w.b.。取10kg小麥樣品，放置在太陽光下晾曬24h，測得其含水率為10.60% w.b.，再取20kg小麥樣品，分成2份，各自加適當(dāng)?shù)恼麴s水，然后將其裝入塑料袋中封閉好，放置恒溫箱中，溫度選定5℃，一周后從恒溫箱中取出，測得兩份小麥樣品含水率分別為14.22%和16.13% w.b.。用標(biāo)準(zhǔn)烘箱干燥法將10g樣品在130℃下干燥19h，重復(fù)3次，測定小麥的含水率（ASAE標(biāo)準(zhǔn)，2001a）[11]。這樣，實驗用的小麥的含水率分別為10.60% w.b.、12.66% w.b.、14.22% w.b.和16.13% w.b.。

1.2 實驗儀器

應(yīng)變控制式三軸儀（TSZ-6A）：南京土壤儀器廠有限公司;糧食孔隙率測定儀（LKY-1）：南京土壤儀器廠有限公司。

1.3 應(yīng)力-應(yīng)變關(guān)系本構(gòu)模型

本文采用修正劍橋模型。修正劍橋模型是一個用塑性增量理論描述應(yīng)力-應(yīng)變關(guān)系的彈塑性本構(gòu)模型[12]。在外力作用下，物體產(chǎn)生的增量變形包括體積應(yīng)變和剪切應(yīng)變，分別由彈性變形和塑性變形兩部分組成：

式中：為彈性體積應(yīng)變增量;為彈性剪切應(yīng)變增量;為塑性體積應(yīng)變增量;為塑性剪切應(yīng)變增量。

修正劍橋模型本構(gòu)關(guān)系就是彈性應(yīng)力應(yīng)變關(guān)系與塑性應(yīng)力應(yīng)變關(guān)系。在修正劍橋模型中，廣義剪切力，平均主應(yīng)力;破壞點時，。

1.3.1 彈性應(yīng)力應(yīng)變關(guān)系

1.3.2 塑性應(yīng)力應(yīng)變關(guān)系

1.3.3 修正劍橋模型

選定筒倉的幾何尺寸與力學(xué)參數(shù)泊松比ν與彈性模量E;測定小麥的修正劍橋模型（公式（8）～（12））參數(shù)e、ν、E、M、κ、λ。采用有限元方法，使用ABAQUS軟件求解修正劍橋模型可計算出筒倉中小麥堆的應(yīng)力分布。

2 結(jié)果與分析

2.1 小麥的修正劍橋模型參數(shù)

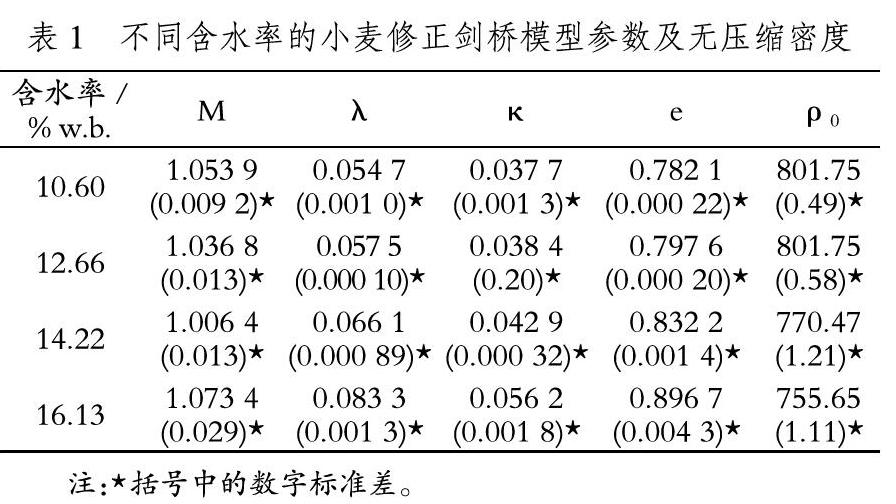
使用HGT-1000A容重器測定小麥堆無壓縮密度（糧倉表層小麥密度）ρ0;使用LKY-1型糧食孔隙率測定儀測定小麥堆的修正劍橋模型參數(shù)孔隙比e;使用TSZ-6A應(yīng)變控制式三軸儀測定小麥的修正劍橋模型參數(shù)E、M、κ、λ。測定的參數(shù)值如表1所示。

2.2 筒倉中小麥的應(yīng)力分布

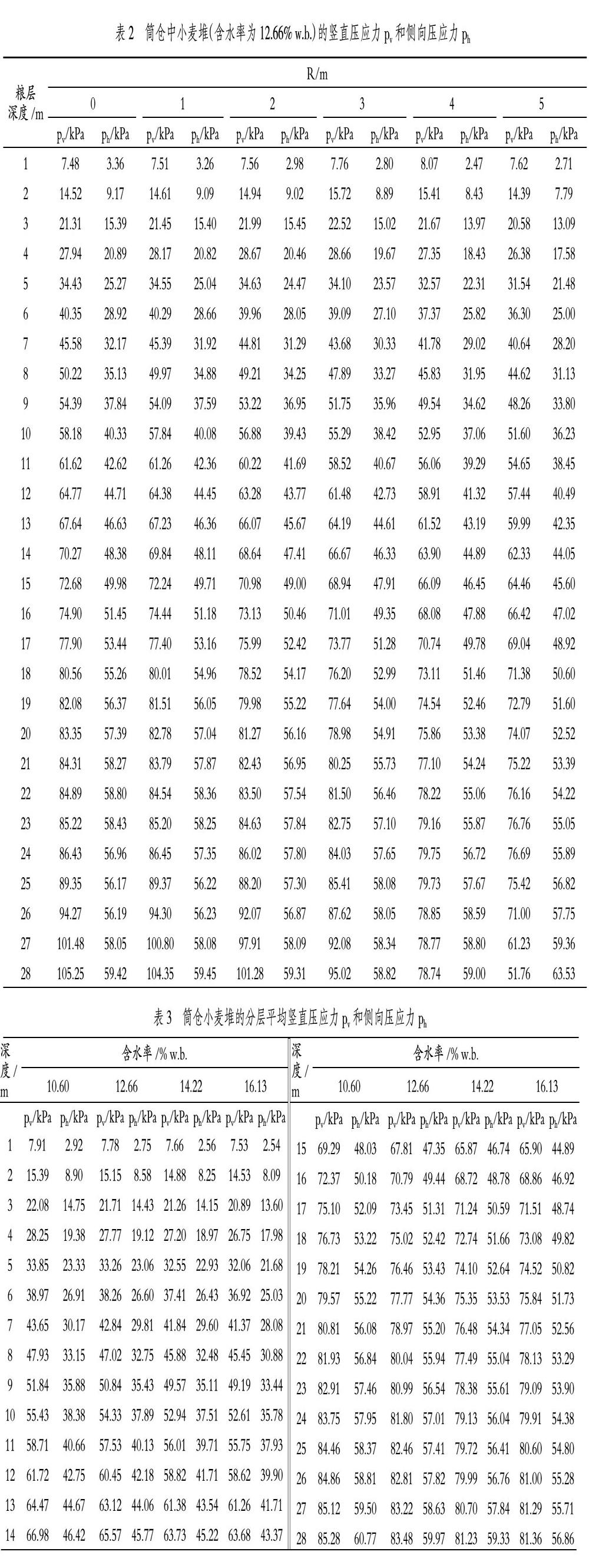
選定筒倉為直徑10m、高31m的薄壁平底圓柱形鋼倉。楊氏模量為2.1×108kPa，泊松比為0.30，倉壁與小麥的摩擦系數(shù)取0.4[13]。筒倉內(nèi)小麥堆高30m，選定的小麥?zhǔn)菬熮r(nóng)19，調(diào)制的含水率分別為10.60% w.b.、12.66% w.b.、14.22% w.b.和16.13% w.b.。表1給出了小麥的修正劍橋模型參數(shù)，泊松比取0.30。筒倉內(nèi)的小麥堆平均分為30個小圓薄層和5個徑向圓柱和圓筒，有限元化分糧堆共150個單元。利用ABAQUS計算出的小麥堆的豎直壓應(yīng)力和側(cè)向壓應(yīng)力如表2～表3、圖1～圖5所示。

2.2.1 小麥堆的應(yīng)力隨離倉軸徑向距離的變化

由表2和圖1可知，在相同含水率和相同糧層深度下，隨著離倉軸徑向距離的增大，小麥堆的豎直壓應(yīng)力減小，糧層越深，豎直壓應(yīng)力減小率越大。3m深處，豎直壓應(yīng)力從中心處的21.31kPa減小到倉壁處的20.58kPa，減小率3.4%;15m深處，豎直壓應(yīng)力從中心處的72.68kPa減小到倉壁處的64.46kPa，減小率11.4%;27m深處，豎直壓應(yīng)力從中心處的101.48kPa減小到倉壁處的61.23kPa，減小了39.7%。

由表2中的數(shù)據(jù)和圖2可知，在相同含水率和相同糧層深度下，隨著離倉軸徑向距離的增大，側(cè)向壓應(yīng)力逐漸減小，糧層越深，側(cè)向壓應(yīng)力減小率越小。3m深處，側(cè)向壓應(yīng)力從中心處的15.39kPa減小到倉壁處的13.09kPa，減小率15.0%;15m深處，側(cè)向壓應(yīng)力從中心處的49.98kPa減小到倉壁處的45.60kPa，減小率8.8%;24m深處，側(cè)向壓應(yīng)力從中心處的56.95kPa減小到倉壁處的55.89kPa，減小率1.9%;糧層接近底部，隨著離倉軸徑向距離的增大，側(cè)向壓應(yīng)力逐漸增大。27m深處，側(cè)向壓應(yīng)力從中心處的58.05kPa增大到倉壁處的59.38kPa，增大率2.3%。

2.2.2 小麥堆的應(yīng)力隨糧層深度的變化

由表2和圖3可知，在相同含水率和相同離倉軸徑向距離下，隨著糧層深度的增大，小麥堆的豎直壓應(yīng)力增大，但靠近倉底與倉壁拐角處的豎直壓應(yīng)力反而減小;離倉軸徑向距離4m處，豎直壓應(yīng)力從糧層深度24m處的79.75kPa減小到糧層深度28m處的78.74kPa;在倉壁處，豎直壓應(yīng)力從糧層深度24m處的76.69kPa減小到糧層深度28m處的51.76kPa。

由表2中的數(shù)據(jù)和圖3可知，在相同含水率和相同離倉軸徑向距離下，隨著糧層深度的增大，小麥堆的側(cè)向壓應(yīng)力增大，但靠近倉底中心處的側(cè)向壓應(yīng)力先減小再增加。

由表3中的數(shù)據(jù)和圖4、圖5可知，在相同含水率下，隨著糧層深度的增大，小麥層的平均豎直壓應(yīng)力、平均側(cè)向壓應(yīng)力增大;隨著深度的增加，應(yīng)力增大率減小。

2.2.3 小麥堆的分層平均應(yīng)力隨含水率的變化

由表3中的數(shù)據(jù)和圖4、圖5可知，隨著含水率的增加，小麥層的平均側(cè)向壓應(yīng)力減小。小麥層的平均豎直壓應(yīng)力與含水率不相關(guān)。

3 結(jié) 論

利用修正劍橋模型和有限元方法對平底倉中豎直壓應(yīng)力和側(cè)向壓應(yīng)力分布進行了模擬。根據(jù)計算結(jié)果可以得出以下結(jié)論：

（1）在相同糧層深度下，隨著離倉軸徑向距離的增大，小麥塊的豎直壓應(yīng)力減小，糧層越深，豎直壓應(yīng)力減小率越大;隨著離倉軸徑向距離的增大，小麥塊的側(cè)向壓應(yīng)力逐漸減小，糧層越深，側(cè)向壓應(yīng)力減小率越小;糧層接近底部，隨著離倉軸徑向距離的增大，小麥塊的側(cè)向壓應(yīng)力反而增大。

（2）在相同離倉軸徑向距離下，隨著糧層深度的增大，小麥塊的豎直壓應(yīng)力增大;糧層接近底部，靠近倉壁處的小麥塊豎直壓應(yīng)力隨著深度的增加反而減小;隨著糧層深度的增大，小麥塊的側(cè)向壓應(yīng)力增大，糧層越深，側(cè)向壓應(yīng)力增大率越小;但靠近倉底中心處的糧塊側(cè)向壓應(yīng)力隨著深度的增加先減小再增加;小麥層的平均豎直壓應(yīng)力、平均側(cè)向壓應(yīng)力隨著深度的增加而增大，增大率隨著深度的增加而減小。

（3）隨著含水率的增加，小麥層的平均側(cè)向壓應(yīng)力減小;小麥層的平均豎直壓應(yīng)力與含水率不相關(guān)。

參考文獻

[1] Thompson S A，Ross I J.Compressibility and Frictional Coefficients of Wheat[J].Transactions of the ASAE，1983，26（4）：1171-1176.

[2] Janssen，H.A.Versuche über getreidedruck in silozellen[J].Zeitschriff des Vereines Deutscher Ingenieure.1985（39）：1045-1049.

[3] Roberts A W.Particle Technology—Reflections and Horizons： An Engineering Perspective[J].Chemical Engineering Research & Design，1998，76（7）：775-796.

[4] Haque，Ekramul.Estimating bulk density of compacted grains in storage bins and modifications of Janssen's load equations as affected by bulk density[J].Food Science & Nutrition，2013，1（2）：150-156.

[5] Vidal P，Gallego E，Guaita M，et al.Finite element analysis under different boundary conditions of the filling of cylindrical steel silos having an eccentric hopper[J].Journal of Constructional Steel Research，2008，64（4）：480-492.

[6] Wang Y，Lu Y，Ooi J Y.Finite element modelling of wall pressures in a cylindrical silo with conical hopper using an Arbitrary Lagrangian–Eulerian formulation[J].Powder Technology，2014（257）：181-190.

[7] Goodey R J，Brown C J，Rotter J M.Rectangular steel silos： Finite element predictions of filling wall pressures[J].Engineering Structures，2017（132）：61-69.

[8] Jofriet J C，Lelievre B，F(xiàn)wa T F.Friction Model for Finite Element Analyses of Silos[J].Transactions of the ASAE，1977，20（4）：735-740.

[9] Mahmoud A，Abdel-Sayed G.Loading on shallow cylindrical flexible grain bins[J].Powder Bulk Solids Technology，1981，5（3）：12-19.

[10] Bishara A G，Ayoub S F，Mahdy A S.Static pressures in concrete circular silos storing granular materials.[J].Journal of the American Concrete Institute，1983，80（3）：210-216.

[11] S352.2 （R2017），Moisture Measurement-Unground Grain and Seeds[S].

[12] 羅汀，姚仰平，侯偉.土的本構(gòu)關(guān)系[M].北京：人民交通出版社，2010.

[13] Moya M，Ayuga F，GuaitaM，et al.Mechanical Properties Of Granular Agricultural materials[J].Transactions of the ASAE，2002，45（5）：1569-1577.