基于復雜分段擬合的熱電廠負荷優化分配

吳月勝，施子福，王樹宇，劉林濤，葛黎明，李 培，周永剛

（1.桐鄉泰愛斯環保能源有限公司，浙江 嘉興 314000；2.能源清潔利用國家重點實驗室（浙江大學），杭州 310027）

0 引言

隨著供熱需求的持續增長，我國熱電聯產機組的規模不斷擴大，目前已占火電機組總容量的30%[1]。然而，由于國家能源結構調整、節能減排壓力不斷加大以及新能源的迅速發展，燃煤機組長期處于非最佳工況下運行[2]，考慮到現有的熱電聯產機組中，供熱方式主要是在汽輪機中壓缸后抽汽加熱熱網水[3-4]，采用此方法供熱，若機組運行不當，極易造成大量高品位能的損失[5]。其原因在于目前熱電廠在實際運行過程中主要采用3 種方法進行熱負荷調節： 熱負荷平均分配；由某一機組帶全部或基本熱負荷，其他機組進行調節；在保證熱網供熱指標的情況下由運行人員自主調節[6]。這3 種方法雖然能滿足熱網需求，但是并沒有考慮汽輪機發電負荷，未能充分優化利用能源，存在能源浪費，影響全廠經濟性。

為了提高熱電聯產機組的經濟性以及響應國家節能減排的號召，需在滿足供熱需求的前提下，在減少蒸汽損耗的同時提高汽輪機發電量，為此，針對發電廠汽輪機性能進行負荷優化分配顯得尤為重要。全廠負荷分配的意義在于： 在一個給定的全廠負荷（發電量）或者變負荷（發電量）的前提下，如何分配各臺機組的負荷，使全廠經濟性最高[7]。此時汽輪機在不同抽汽-排汽組合工況下的性能，即獲得不同抽汽量及排汽量組合下對應的汽輪機進汽量和發電量成為負荷優化分配的關鍵。

目前，科研部門往往通過現場試驗獲得汽輪機性能參數，然而實際運行過程中汽輪機運行狀況復雜，不同中壓抽汽與低壓排氣組合眾多，想要獲得詳盡的性能參數意味著工作量大且成本高；除此之外，實際運行過程中汽輪機運行狀態會隨著供汽量的變化而變化，很難連續維持在試驗需要的理想穩定工況。因此，基于某發電廠汽輪機實際運行數據進行深入數據挖掘，通過對比不同方法，最終獲得汽輪機實際運行狀態下不同中壓抽汽和低壓排汽組合下的網格化性能計算方法，在保證計算精的前提下減少工作量以及工作成本，為負荷優化分配計算提供理論基礎，保證各臺汽輪機在較優工況下運行，提高機組的經濟性，降低供熱、發電煤耗[8-9]，減少地區或全社會的能源浪費，推進資源節約型、環境友好型社會建設[10-12]。

1 汽輪機性能計算方法

以某熱電聯產機組為例，2 臺汽輪機型號為CB30-13.24/3.5/0.981，超高壓高溫單缸抽汽背壓機，設計進汽量為304.5 t/h，最大抽汽量為80 t/h，包含2 臺高壓加熱器，熱力系統如圖1 所示。

首先對單臺汽輪機數據進行分析，數據點時間間隔為5 min，總時長為273 天，單個指標數據量達到78 624 個。認為汽輪機進汽量低于90 t/h時汽輪機處于啟停過程，以下分析不包含此部分數據。

圖1 機組熱力系統

1.1 直接非線性曲面擬合法（方法1）

通常而言，汽輪機進汽量和發電量與其中壓抽汽量與低壓排汽量有關，因此方法1 直接對1號汽輪機進汽量、中壓抽汽量、低壓排汽量進行非線性曲面擬合，擬合公式采用z=z0+ax+by+cx2+dy2+fxy，擬合結果如圖2 所示，擬合得到的公式如式（1）所示。

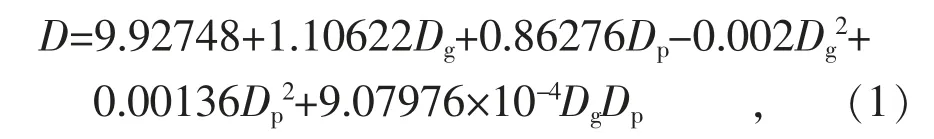
式中： D 為汽輪機進汽流量；Dg為汽輪機中壓抽汽供熱流量；Dp為汽輪機排汽流量。

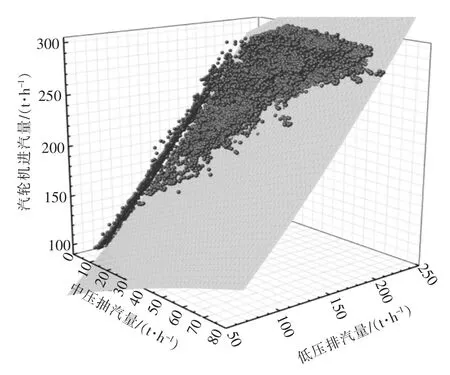
圖2 進汽量、中壓抽汽量、排汽量的非線性曲面擬合

根據式（1）計算得到汽輪機進汽量，與實際進汽量進行比較，如圖3 所示。從圖3 可以看出，汽輪機進汽量實際值多數分布在y=x 兩側，以此擬合會造成1 個實際值與2 個甚至3 個計算值對應，偏差達到0～20 t/h，計算誤差達到10%以上，偏差較大。

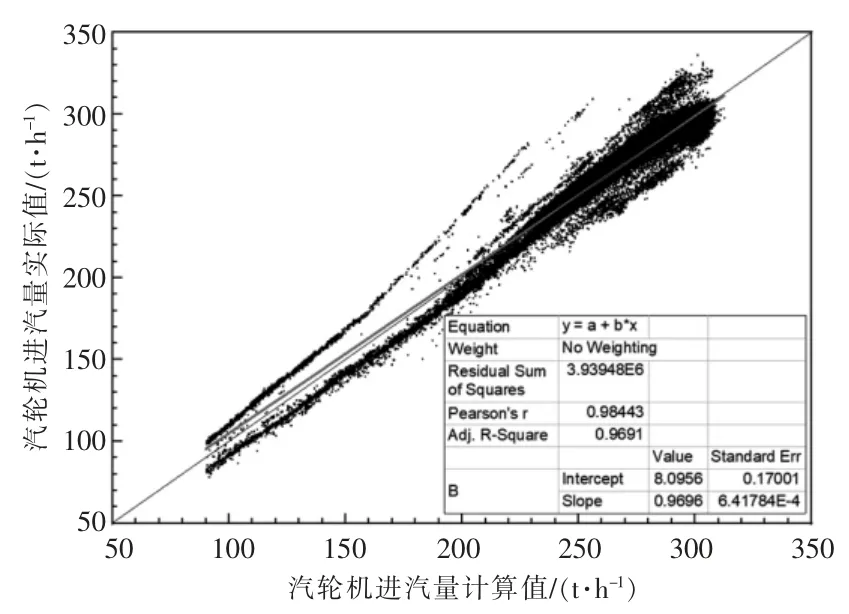
圖3 汽輪機進汽量計算值與實際值對比（方法1）

1.2 中壓抽汽非線性曲面擬合法（方法2）

造成方法1 計算值與實際值偏差較大的原因是沒有考慮中壓抽汽對計算結果的影響。為進一步增加擬合精度，提高全廠負荷優化分配的效果，在此考慮汽輪機純凝運行及抽背運行2 種運行方式，將無中壓供熱及有中壓供熱區別對待。當機組存在中壓供熱時，即剔除中壓抽汽為零的數據，采用方法1 進行曲面非線性擬合，擬合結果如圖4 所示，擬合公式如式（2）所示，使用式（2）對包括有中壓抽汽和無中壓抽汽的情況進行計算，得到的汽輪機進汽量實際值與計算值的關系如圖5 所示，可見，仍有部分數據遠離y=x 曲線，汽輪機進汽量計算值與實際值相比誤差達到10%以上。

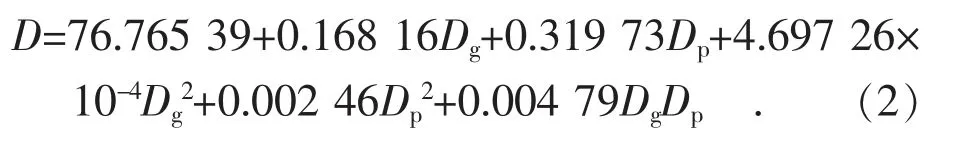
圖4 有中壓供熱汽輪機進汽量計算擬合

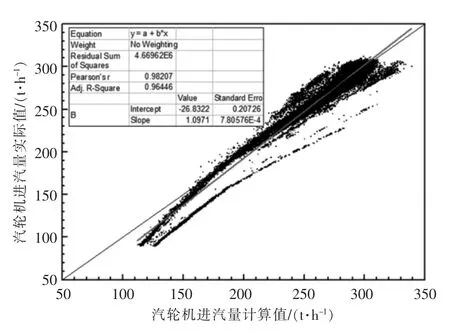
圖5 汽輪機進汽量計算值與實際值對比（方法2）

1.3 復雜分段擬合法（方法3）

方法3 為在方法2 的基礎上進一步考慮汽輪機有、無中壓抽汽供熱2 種情況，當有中壓抽汽時采用上述方法；當無中壓抽汽時，研究發現，汽輪機進汽量與排汽量的關系與是否投運2 臺高壓加熱器有關。當2 臺高加水溫溫升之和小于40℃時，汽輪機進汽量與排汽接近，即兩者差值約為0 t/h，而當2 臺高加水溫溫升之和大于40 ℃時，汽輪機進汽量與低壓排汽量的差值大于0 t/h，以2 臺高加水溫升高之和是否大于40 ℃作為高加是否投運的標志。當無中壓抽汽時，高加投運與否的情況下汽輪機進汽量與低壓排汽量為線性關系，擬合結果如圖6 所示，擬合公式如式（3）、式（4）所示。

未投運高加時：

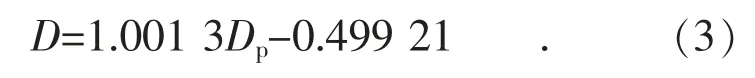
投運高加時：

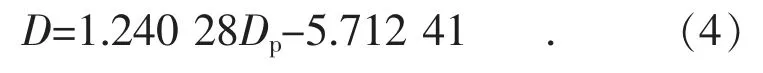
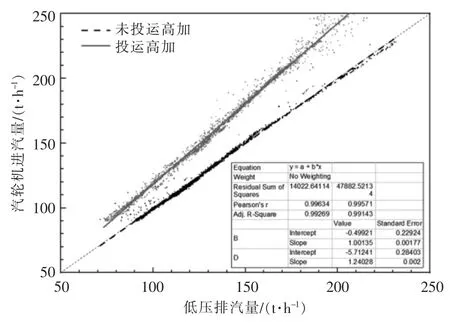
圖6 無中壓抽汽時高加投運與否情況下汽輪機進汽量與低壓排汽量關系

采用方法3 對所有情況進汽量進行計算，得到汽輪機進汽量實際值與計算值的關系如圖7 所示，實際值與計算值的關系為： 計算值≈實際值，擬合效果較好。

1.4 3 種方法精度對比

對比上述不同汽輪機進汽量計算方法，得到不同方法計算值與實際值的百分比偏差見圖8，3種方法校正決定系數依次為0.969 10，0.964 66 和0.999 6，斜率分別為0.969 6，1.097 1 和0.999 6，方法3 最接近y=x；3 種方法平均絕對誤差分別為2.38%，2.80%和1.72%，方法3 誤差最小；結合圖8 還可以看出方法3 計算所得汽輪機發電量與實際值的偏差分布在±10%以內，誤差分布范圍明顯小于方法1 及方法2。綜上，采用方法3計算所得汽輪機進汽量精度更高，與實際值相比偏差更小，可以作為負荷優化分配的依據。

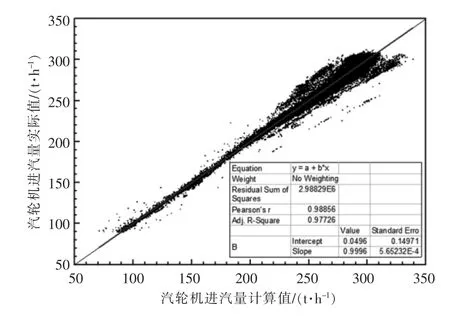
圖7 汽輪機進汽量實際值與計算值的關系（方法3）

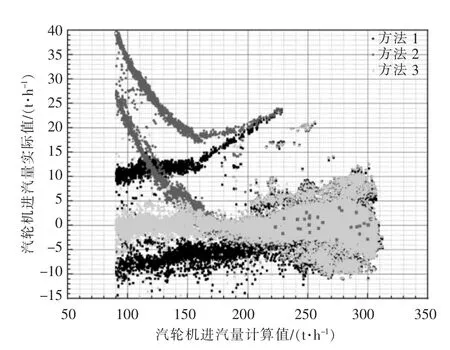
圖8 3 種計算方法誤差對比

1.5 2 臺機組汽輪機進汽量與發電量擬合公式

采用方法3 對2 臺汽輪機進汽量、發電量進行擬合，結果如表1 所示。計算所得值與實際值相比平均絕對誤差均在3%以內，精度較高，以此作為負荷優化分配的理論依據。

負荷優化分配，目的在于： 在滿足外界供熱要求的前提下，基于各機組以及鍋爐的負荷特性差異，通過機組間和鍋爐間負荷的合理優化分配，使得全廠發電效率達到最大，而全廠煤耗率盡可能降低。通過對母管制熱力系統的建模分析以及一系列鍋爐和汽輪機性能試驗，將負荷優化分配的實現分為兩部分進行，即汽機側和鍋爐側。汽機側的優化方式為在滿足供熱總量基礎上，將供熱量進行機組間的分配，通過調整各機組的進汽量，使得發電汽耗率最小；鍋爐側的優化方式為在鍋爐總產汽量滿足汽機側優化后的進汽量基礎上，將產汽量進行鍋爐之間的分配，調整各鍋爐的產汽量，使得全廠產汽煤耗率最小。

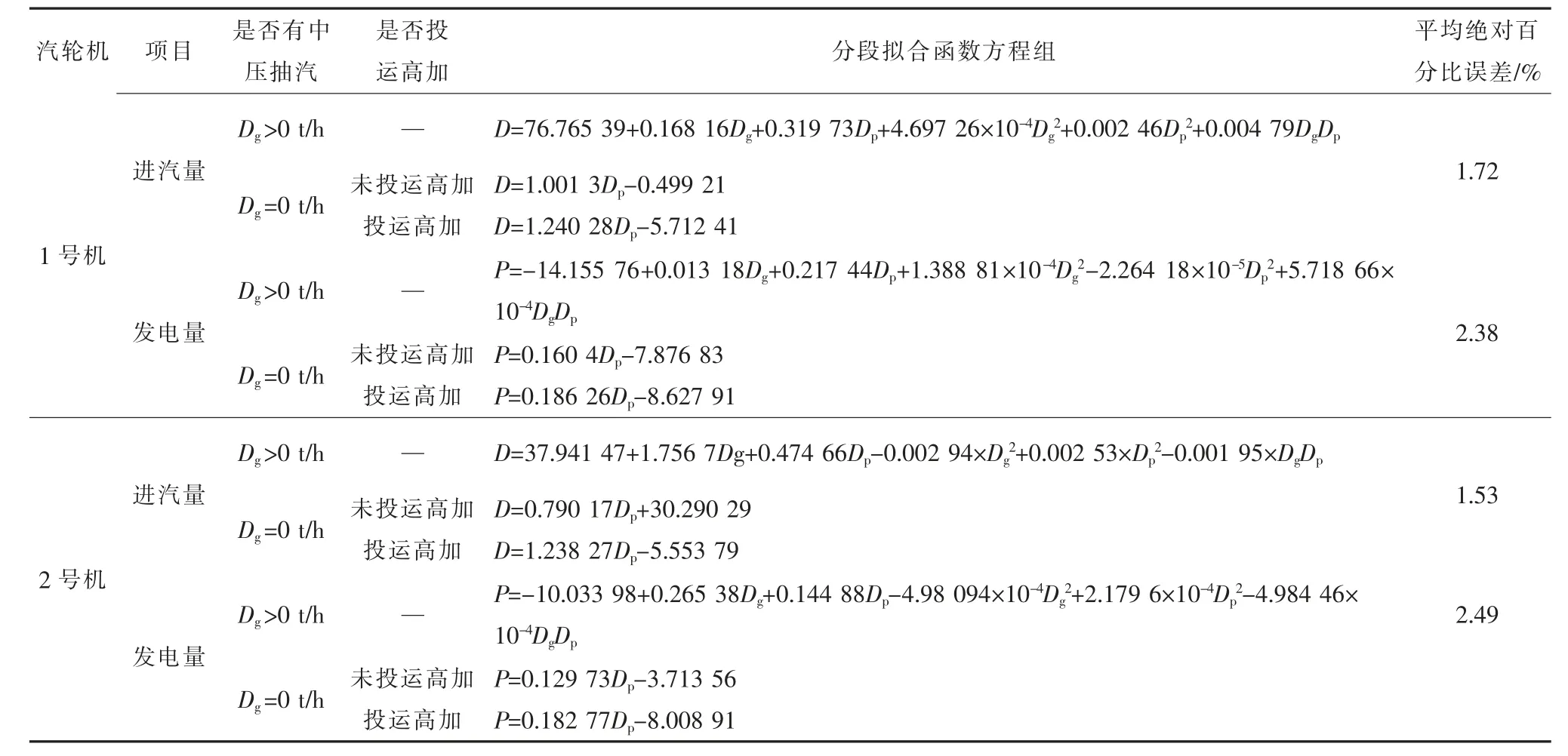
表1 2 臺機組汽輪機進汽量與發電量擬合公式全廠負荷優化分配建模及求解

2 負荷優化分配

2.1 汽輪機側數學模型

汽輪機側有中壓抽汽供熱蒸汽和背壓排汽低壓供熱蒸汽，通過調整各汽輪機的進汽量，背壓機的排汽量和發電量也隨之改變，在排汽總量滿足供熱需求的所有組合中，尋找出整體發電汽耗率最小的分配方式，從而實現機組間熱電負荷優化分配。

根據上述擬合方程，可以得到汽輪機的特性方程，分別為汽輪機進汽流量與排汽流量和抽汽流量的關系方程：

汽輪機發電功率與排汽流量和抽汽流量的關系方程：

負荷優化分配的思路為： 通過汽輪機排汽流量和中壓抽汽流量，計算出對應汽輪機進汽流量和發電功率，計算和比較發電汽耗率的大小，尋找最優的負荷分配方式。

目標函數為發電汽耗率最低：

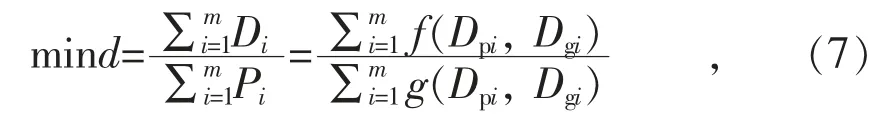
式中： d 為發電汽耗率；m 為汽輪機的數量；Di為第i臺機組的進汽流量；Pi為第i 臺機組的發電功率。

約束條件主要包括汽輪機進汽量在設計范圍內，汽輪機抽汽流量不能超過最大抽汽限制，汽輪機排汽流量和發電功率限制，汽輪機排汽流量滿足供熱需求的等式約束，具體如下：

機組容量約束：

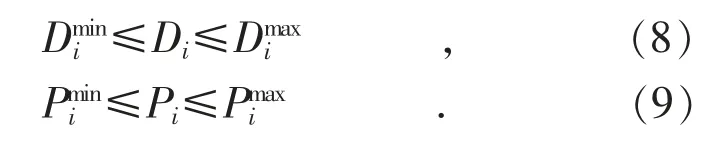
抽汽流量約束：

排汽流量約束：

供熱負荷等式約束：

式中： Dr為供熱總流量。

2.2 鍋爐側數學模型

鍋爐側負荷優化分配是在汽輪機側優化所得的最小汽耗量基礎上，將該蒸汽產量分配到各臺鍋爐上，使得各鍋爐產汽量滿足汽機側所需蒸汽量的同時，整體產汽煤耗率最小。

根據鍋爐性能試驗，可得出各鍋爐效率與產汽量之間的特性方程為：

式中： η 為鍋爐效率；Db為鍋爐產汽量；h（Db）為鍋爐煤耗特性方程。

負荷優化分配的思路為： 通過各鍋爐產汽量計算鍋爐效率，結合給水焓值和主汽焓值以及煤的熱值可推算出各鍋爐煤耗量，最后計算并比較整體產汽煤耗率，得出最佳分配方式。

煤耗量計算公式為：

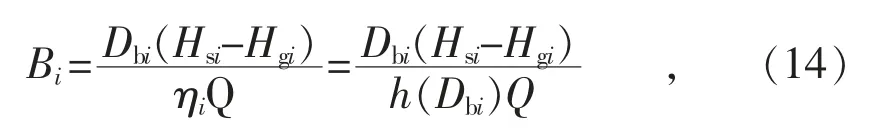
式中： Bi為第i 臺鍋爐煤耗量；Dbi為第i 臺鍋爐產汽量；Hgi為第i 臺鍋爐給水焓值；Hsi為第i 臺鍋爐主蒸汽焓值；ηi為第i 臺鍋爐效率；Q 為燃煤熱值。

目標函數為產汽煤耗率最低：

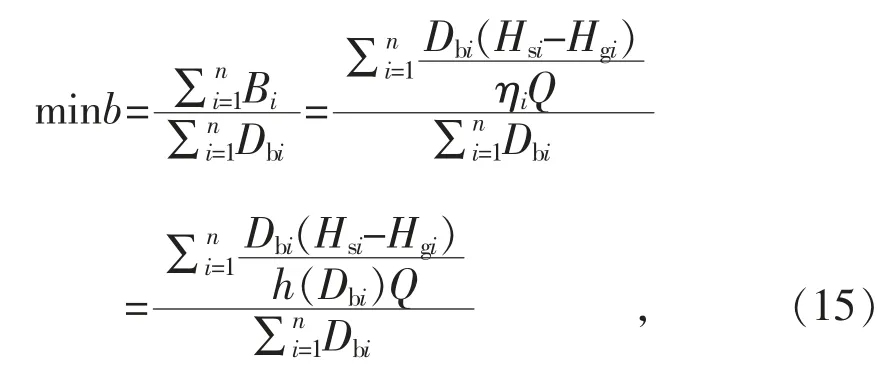
式中： b 為產汽煤耗率；n 為鍋爐數量。

約束條件主要為鍋爐的容量約束，特別注意的是，鍋爐總產汽量要與汽機側負荷優化分配后汽機總進汽量相吻合：

鍋爐容量約束：

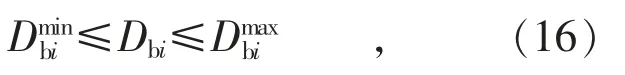
產汽量等式約束：

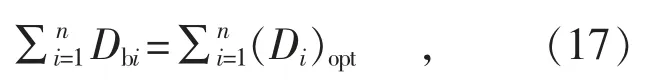
式中： （Di）opt為第i 臺機組負荷優化分配后的進汽流量。

2.3 負荷優化分配算法

負荷優化分配是從SQL 數據庫中讀取某一時刻機組的運行數據。考慮到機組供熱負荷時常迅速變化，而循環流化床鍋爐熱慣性較大，負荷變化能力及速率有限，假如負荷優化區間為整個負荷范圍，機組沒有能力迅速做出相應負荷的響應，反而使得鍋爐或汽輪機長期處于變工況狀態，造成能耗大幅升高，無法實現“全廠最優”。因此本文在兼顧負荷變化速率的同時達到“全廠最優”，即只在該工況附近進行尋優查找，找出最優的分配方式。該母管制機組分配過程中考慮的參數較少，計算過程并不復雜，計算要求相對簡單，因此可以將尋優的區間離散化，選擇合適的步長，在滿足供熱負荷要求的前提下，用遍歷的方式來找到全局的最優解。使用窮舉法一方面是基于相對簡單的計算過程，使得計算機性能能夠滿足計算要求，另一方面可以保證解的最優性，即在尋優的范圍內計算結果一定是最優解。汽輪機側及鍋爐側負荷優化分配算法流程如圖9、圖10 所示。

圖9 汽機側負荷優化分配算法流程

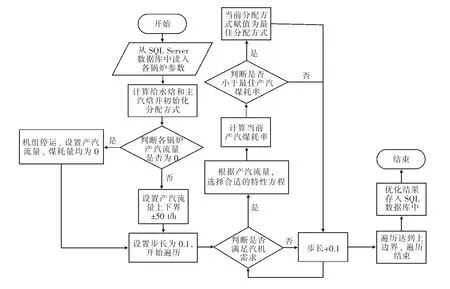
圖10 鍋爐側負荷優化分配算法流程

汽機側和鍋爐側兩側算法分步實現，汽機側先根據供熱負荷需求通過算法使得發電汽耗率最小，再把汽輪機優化后的進汽總量優化分配到各鍋爐，使得產汽煤耗率達到最小。算法程序可在滿足某一時刻供熱需求的前提下，通過汽輪機間和鍋爐間的負荷優化分配，使得全廠的發電汽耗率以及產汽煤耗率達到最小，從而達到節能降耗的效果。

3 經濟效益分析

隨機采集機組連續一周的歷史運行數據（2019 年11 月4—11 日），在滿足中、低壓供熱需求的前提下，采用上述方法對全廠三爐兩機進行基于效率最優的負荷優化分配，總標煤耗量及總發電量變化值如圖11 所示，變化值均為優化后減去優化前，負值為降低，正值為增加。

根據圖11 中數據，計算得到優化后總標煤耗量平均降低0.415 t/h，總發電量平均增加0.101 MW/h，按年運行6 000 h 計，2019 年下半年入廠煤標煤單價平均值約862.58 元/t，上網電價（含稅）為0.505 8 元/kWh 估算，負荷優化分配后可降低生產成本約245.43 萬元/年。

4 結論

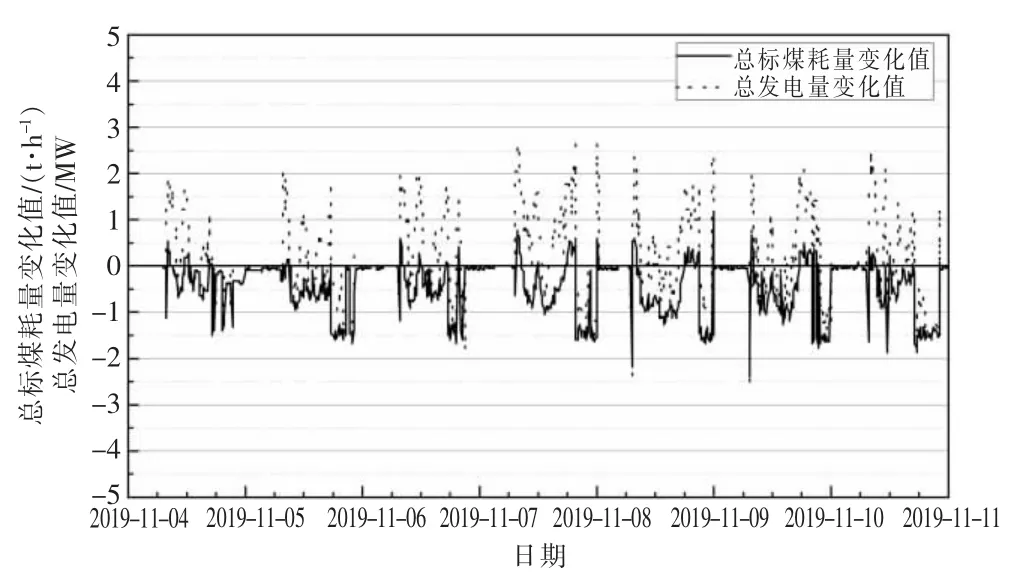
圖11 優化后總標煤耗量與總發電量變化值

（1）采用考慮是否有中壓抽汽、是否投運高加的復雜分段擬合方法得到2 臺汽輪機的進汽量與發電量，該計算結果與實際值相比，平均絕對誤差均在3%以內，精度較高，計算值可以代表實際值，可以作為全廠負荷優化分配數學模型的理論依據。

（2）通過建立數學模型，采用窮舉法，在滿足汽輪機側以及鍋爐側運行要求及供熱要求的基礎上，對全廠負荷分配進行優化，優化后可實現總標煤耗量平均降低0.415 t/h，總發電量平均增加0.101 MW/h，全年生產成本降低約245.43 萬元。