基于多層感知機的密封繼電器PIND信號識別

李 響 蔣愛平 楊世華 薛永越 王國濤，2

(1.黑龍江大學電子工程學院，哈爾濱 150008;2.哈爾濱工業大學電器與電子可靠性研究所，哈爾濱 150001;3.上海航天設備制造總廠有限公司，上海 200245)

1 引 言

在密封電子元器件的生產過程中，由于設計水平工藝條件的限制，會由于各種外界原因，引入材質不同大小不一的多余物顆粒[1]。某些多余物顆粒在航天繼電器使用之前的各項檢測中未被檢測出來，殘留在腔體內部的某個部位未被發現。在航天使用的過程中，由于受到外界環境的影響被激活，游離于腔體內，對器件產生嚴重危害[2～4]。一旦未檢測出密封繼電器內的多余物就會造成不可預知的影響。在目前的設計水平、工藝條件下很難完全避免多余物的產生。因此，在密封電子元器件使用之前對其進行多余物檢測可以較好地提高設備和模塊的工作可靠性，降低故障率。

現階段使用的相關鑒定方法主要包括：顯微鏡觀察法、X光照相法、MATARA方法及微粒碰撞噪聲檢測(Particle Impact Noise Detection，PIND)法等[5]。其中，PIND檢測方法是目前主要的檢測方法，經常用于各種密封電子元器件的出廠檢測[6]。經過長期的發展和完善，該檢測方法日漸成熟，但是PIND方法的檢測精度并不理想，有多種影響因素，其中組件信號干擾是導致檢測精度不高的重要原因[7]。組件信號是在外部正弦振動激勵下，試件內部可動部件產生受迫振動而檢測到的固有機械信號。

學者前期在對PIND試驗方法進行拓展研究時，發現組件信號具有時域上周期性的變化[8]。高宏亮在前人研究的基礎上，進一步針對航天繼電器多余物檢測中組件信號展開了研究，同樣認為組件脈沖總是等周期的出現。基于該特性，認為得到對應脈沖發生時刻序列近似為等差序列，時間間隔序列則近似為常數序列[9]。烏英嘎等對組件信號頻譜特性做過進一步的研究，認為組件信號的頻譜相對于多余物信號較窄[10]。

目前針對組件信號與多余物信號的檢測方法，只是依靠單一時域特性(周期性)的相似度進行聚類。但大量實驗數據表明,單個組件信號脈沖特征不論在時域還是頻域和多余物信號脈沖特征的相似程度較高,區分二者較為困難；另外，以往對密封電子元器件組件信號的研究和分類不夠深入，認為組件信號的表現形式僅為不同周期內連續存在的單組脈沖序列，而實際上要復雜的多；這些因素都會導致某些組件信號被誤判為多余物信號。并且跟據檢測現場的統計結果，目前廣泛使用的4511系列和DZJC系列多余物檢測系統，對多余物信號和組件信號的識別準確率約為75%，誤判率較高。為降低組件信號和多余物信號的誤識別率，提高多余物檢測精度，本文在總結前人研究的基礎上，分析現存有待解決的問題，提出了以下的識別方法。

文中提出一種基于多層感知機神經網絡的多維條件下密封繼電器PIND信號識別方法，首先對多余物信號和組件信號的產生原理進行分析并其進行信號特征提取和選擇。然后建立了基于多層感知機的密封繼電器PIND信號識別模型，并根據多維條件下影響密封繼電器PIND信號檢測準確度變動數據的具體特征，對神經網絡模型采取網絡結構優化和參數針對性調整。最后使用測試樣本集進行改進后模型的驗證，實驗結果驗證了該模型的準確性和有效性。

2 試驗數據的獲取

本文使用的數據集是由元器件生產方提供的檢測數據和研究人員自行采集的試驗數據共同組成的。所有試驗數據均使用哈爾濱工業大學設計的DZJC-III型多余物自動檢測系統采集，該系統如圖1所示。在檢測系統中對傳入的被檢測聲音信號進行處理，建立檢測信號的數據樣本集[7]。

圖1 DZJC-III型多余物自動檢測系統

3 多余物信號與組件信號的特征分析

3.1 多余物信號與組件信號介紹

多余物信號是已經被激活多余物微粒與密封電子元器件內部相關組成機構或密封內壁碰撞產生的。振動發聲信號是通過聲發射傳感器以一定的電壓量表現出來的信號。在每次碰撞過程中，隨機產生一個單邊震蕩衰減的脈沖。多余物信號主要表現為隨機性的尖峰脈沖序列，單個脈沖呈單邊振蕩衰減趨勢，即脈沖初始幅值上升速度快，當其達到一定峰值迅速衰減。

組件信號是密封電子元器件可動組件自行振動激活所產生的信號。組件信號主要表現為具有周期性尖峰脈沖序列，必須具有一定的起振過程才能使可動部件被激活，當外界沖擊消失，其又需要一定的時間才能回到靜止狀態。典型的多余物信號脈沖序列和組件信號脈沖序列如圖2所示。

圖2 典型多余物信號脈沖序列和組件信號脈沖序列

由于多余物信號和組件信號有以上的差異，可以利用這些差異對二者進行區分，分別從時域和頻域兩方面計算信號特征。

3.2 多余物信號與組件信號的特征選擇

對檢測系統提取到的脈沖信號由MATLAB程序，將脈沖處理成可用的數據，對數據清洗，去除異常值后進行特征選擇。

在特征選擇中我們主要從以下角度考慮：特征是否發散;特征越發散對樣本的群分能力越強。特征與目標的相關性;與目標相關性高的特征，應當優先選擇。總的來說特征選擇是選擇與目標相關性強、且特征彼此間相關性弱的特征子集[11，12]。

我們分別從時域和頻域兩方面統計收集了近年來常用的且具有代表性的14個特征，并對這14個特征進行特征選擇。本文選用了兩種方法分別是卡方檢驗和基于樹模型的特征選擇方法。卡方檢驗法的目標就是檢驗特征與分類目標的相關性程度。卡方檢驗值越大，相關性越強。選用基于樹模型的特征選擇方法目的是計算每個特征對模型的重要程度。試驗結果如圖3所示。由圖可知特征zerorate在卡方檢驗中得分最高，說明其與分類目標的相關性最強。MSFcha特征對于模型分類準確度影響最為重要。

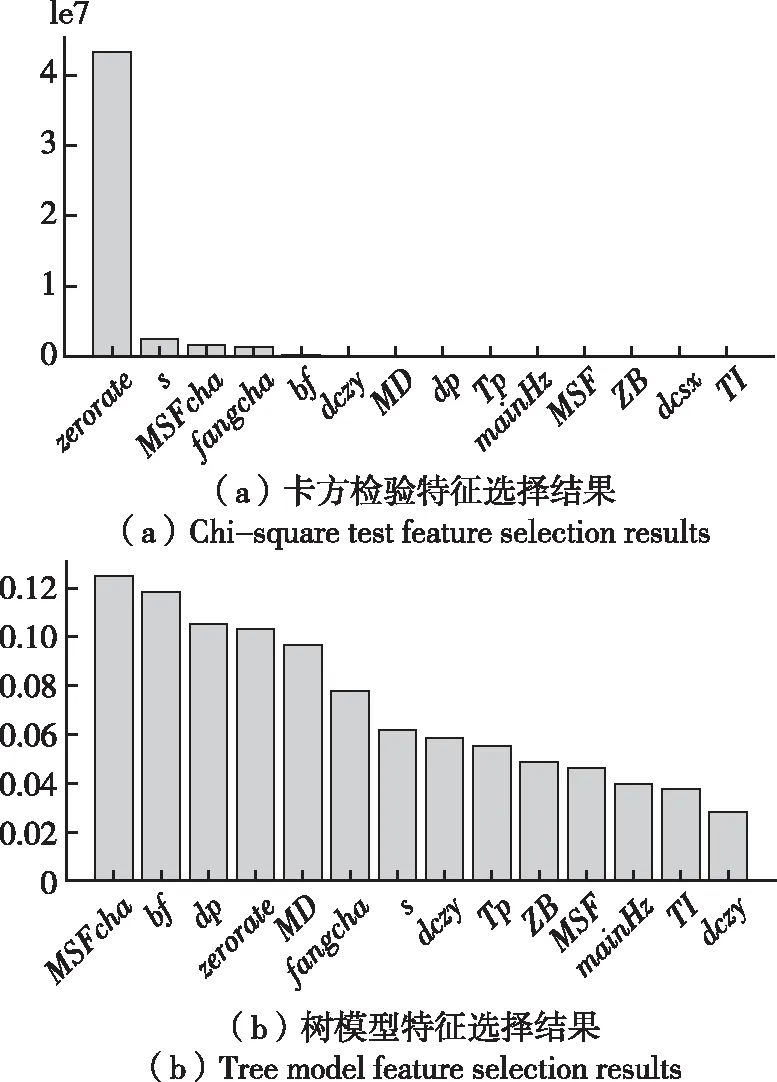
圖3 特征選擇結果圖

本文還嘗試采用PCA對數據特征進行了數據降維，用處理后的四維特征數據進行模型訓練后發現，雖然整體的準確率有所提高，但是多余物信號的召回率、精度、以及F1-score值都明顯低于經過卡方檢驗和基于樹模型所選出的特征所進行訓練后的結果。在分類器模型評價時，僅選用準確率這一單一評價指標不足以表明分類器的提升程度和整體性能。并且PCA方法所獲得的主成分特征的物理意義不明確，對后續研究的特征工程不能給出很好的啟示作用。因此本文在特征選擇方面沒有使用PCA方法。

表1 結果對比Tab.1 Comparisonofresults方法類別PrecisionRecallF1-scoreAccuracy卡方檢驗和基于樹模型多余物0.870.700.7887.1%PCA多余物0.520.130.2189.3%

如表1所示，通過對比分析試驗結果且綜合考慮各個特征的區分度和計算速度，選取出了以下四個特征分別為頻譜質心s、頻率均方根MSFcha、峰值因子bf、過零率Zerorate。

頻譜質心s表現了信號脈沖的集中程度和集中位置如公式(1)所示：

(1)

式中：f2——頻譜下限截止頻率；f1——頻譜下限截止頻率；f——信號脈沖；X(f)——信號的頻率幅度譜。

頻率均方根MSFcha即對單個脈沖的頻譜數據計算其具體的方差，其表示頻率對于其中心頻率的離散程度如公式(2)所示：

(2)

式中：PSD——已知功率譜密度的離散信號；N2、N1——分別是起始和終止信號。

峰值因子bf表現了峰值在波形中的極端程度如公式(3)所示：

(3)

式中：Vmax——PIND信號的峰值電壓；VRMS——PIND信號的電壓有效值。

過零率Zerorate表示單位時間內信號通過零點的次數如公式(4)所示：

(4)

式中：N——一幀的長度；sgn[]——符號函數；Sω(n)——輸入信號。

4 模型的構建與測試

卷積神經網絡(Convolutional Neural Networks)適合處理大型圖像等復雜的情況，特征維數多，數據量大的樣本。本文樣本數據數量以及特征維數較少，使用復雜的模型使得網絡結構復雜化，不僅增加了網絡模型的訓練時間，同時也更容易使模型出現過擬合現象。相對比多層感知機模型結構更靈活，所實現功能更適合于本文樣本數據。

多層感知機(Multilayer Perceptron，MLP)的結構如圖4所示，除了第一層的輸入層和最后一層的輸出層，它中間可以有多個隱含層，不同層之間是全連接的。多層感知機是一種誤差反向傳播的多層前饋神經網絡算法。在隱含層中通過選用不同的激活函數能夠給神經元引入非線性因素，這樣可以將神經網絡運用到更多的非線性模型中。

圖4 多層感知機結構圖

4.1 試驗數據

本文使用的數據集是由元器件生產方提供的檢測數據和研究人員自行采集的試驗數據共同組成的。每條數據由四個特征值和一個分類標簽組成，經過預處理后共包括196297組數據，其中多余物數據63611組，組件數據132686組，按3∶1的比例隨機抽取出訓練集和測試集。數據集的具體描述如表2所示。

表2 樣本數據信息Tab.2 Sampledatainformation多余物個數組件個數總數訓練集4770799515147222測試集159043317149075總數63611132686196297

在訓練模型過程中要輸入多維特征數據，但由于特征性質的不同，特征的數值范圍會相差很大，一些過大或過小的數據會影響模型的訓練，從而影響分類結果。此外，數據分布范圍很廣也會影響訓練結果。所以在訓練模型前需要對原始特征數據集進行標準化處理，以保證模型訓練結果的準確性。本文將特征中的數值進行標準差標準化，即轉換為標準的正態分布。其轉化函數為

X*=(x-μ)/σ

(5)

式中：X*——標準化后的值；x——原始數據值；μ——原始數據的均值；σ——原始數據的標準差。

最后得到的新的數據的均值就是0，方差1。

4.2 評價指標

在分類器模型評價時，僅選用準確率這一單一評價指標不足以表明分類器的提升程度和整體性能，所以選用召回率(Recall)、精度(Precision)作為評價指標。

Accuracy=(TP+TN)/(TP+FN+FP+TN)

(6)

式中：Accuracy——準確率；TP——被正確分類的正類樣本數量；TN——被正確分類的負類樣本的數量；FN——被錯誤分類的正類樣本的數量；FP——被錯誤分類的負類樣本的數量。

Recall=TP/(TP+FN)

(7)

Precision=TP/(TP+FP)

(8)

則精度和召回率的調和均值F1-score:

F1-score=2×(Precision×Recall)/(precision+Recall)

(9)

由于召回率體現了分類模型對正類樣本的識別能力。在信號識別領域更加側重的是信號被正確檢測出的概率，也就是分類器模型評價指標中的召回率。而F1-score相當于精度和召回率的綜合評價指標，它體現了分類模型的穩健程度。綜上考慮，本文在評價分類模型性能時更加注重召回率和F1-score值的變化。

4.3 超參數的選擇

超參數是用來確定模型的一些參數。對于神經網絡模型的訓練來說，超參數的選取起著極其重要的作用[13]。為了使網絡模型的結構最優，分類的準確度最高，整體性能最好，本文對隱含層的層數、單層的節點數量(hidden-layer-sizes)、隱含層激活函數(activation)和權重優化算法(solver)這四個常用影響參數進行調優。文中采用網格搜索法搜索多層感知機模型的最佳結構，選取使模型性能最好的超參數組合。

首先對隱含層的層數進行縱向對比選擇，不同隱含層數對分類結果的影響如表3所示。

表3 不同隱含層數模型結果對比Tab.3 Comparisonofdifferenthiddenlayermodelresults隱含層層數損失值準確率10.357585.74%20.348985.94%30.345786.18%40.355385.70%

表3比較了隱含層的層數對感知機模型分類性能的影響。從表中可以看出，隨著層數的增加，由損失函數計算出的當前損失值在逐漸減小，但當層數為4時損失值上升。同時隨著層數的增加準確率也在不斷的上升，但在層數為4時準確率下降。這是因為隨著隱含層層數的增加使得網絡結構復雜化，不僅增加了網絡模型的訓練時間，同時也更容易使模型出現過擬合現象。結合實驗情況和實際情況綜合考慮，在隱含層數為2和3時總體性能接近。3層隱含層模型結構較復雜，訓練時間較長但性能提升效果不明顯，所以最終選擇隱含層層數為兩層。

然后對單層神經元節點數目進行選擇，在這里我們先對單層神經元個數范圍進行粗略選擇。運用網格搜索法在神經元節點個數范圍為[20,211]內進行粗略尋優，初步確定神經元節點個數的最佳范圍。實驗結果如圖5所示。

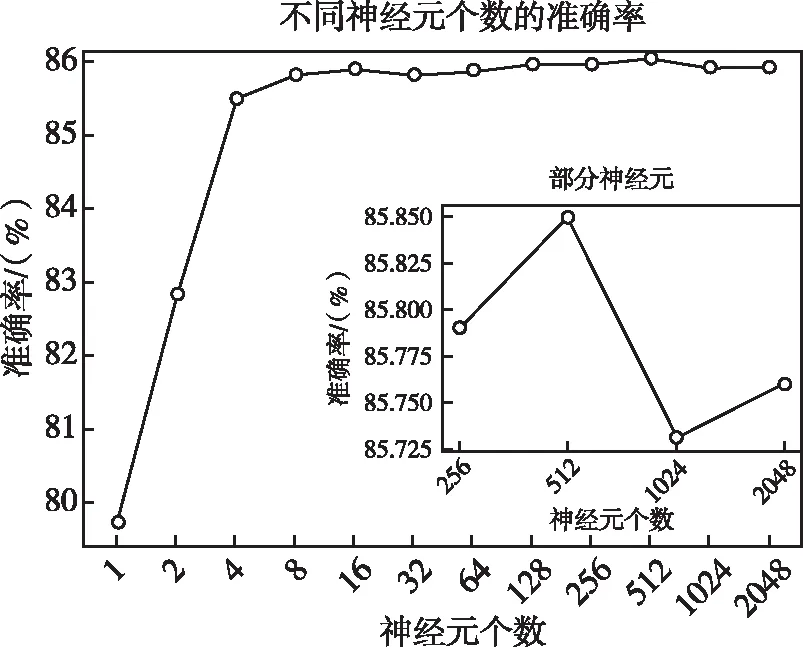
圖5 單一層神經元節點個數性能對比

由圖5可以看出神經元節點個數為512時模型整體準確率最高，所以我們可以初步確定神經元節點個數最佳范圍為[450，550]。

最后采用網格搜索法對隱含層激活函數和權重優化算法以及精細范圍神經元個數進行尋優。

采用交叉驗證方法對訓練樣本進行測試[14]，如表4所示。本文設置K=3，即3折交叉驗證。經過網格搜索法和交叉驗證法對多層感知機在二分類任務中的超參數組合得到調優結果。效果最好超參數(activation,solver,hidden-layer-sizes)分別為(relu,lbfgs,527)，在測試集上能達到的最高分類準確率為87.1%。

表4 參數范圍選取Tab.4 Parameterrangeselection優化參數名稱優化參數范圍隱含層激活函數(activation)‘tanh’,‘relu’,‘logistic’權重優化算法(solver)‘sgd’,‘adam’,‘lbfgs’單層的節點數量(hidden-layer-sizes)(450,550)

4.4 試驗結果

本文設定神經網絡隱含層層數為2，單層神經元個數為527，隱含層激活函數為relu，權重優化算法為lbfgs的超參數組合對49075組測試集數據進行分類。為了驗證算法的有效性，同時也使用了機器學習中常用分類算法決策樹(DecisionTree)算法進行測試。測試結果如表5所示。

表5 測試結果對比Tab.5 Comparisonoftestresults算法類別PrecisionRecallF1-scoreAccuracy多層感知機算法多余物0.870.700.78組件0.870.950.9187.1%決策樹算法多余物0.710.720.72組件0.820.810.8281.3%

通過對比決策樹算法證明了運用多層感知機算法檢測信號的模型是可靠的。由表5可知運用多層感知機算法對信號進行檢測其分類準確率達到87.1%，對多余物和組件信號的檢測精度均為0.87，其中組件信號召回率為0.95高于多余物信號召回率為0.7。組件信號F1-score值為0.91高于多余物信號F1-score值為0.78。經初步分析，筆者認為此結果是由于多余物信號樣本與組件信號樣本數據集不平衡所導致，在后續的研究中會對其進行深入研究。總體來說分類模型的穩健程度較好。

5 結束語

本文提出的基于多層感知機的航天繼電器內組件信號識別方法，選取了組件信號和多余物信號時域和頻域上的頻譜質心、頻率均方根、峰值因子、過零率作為特征量。經實驗分析后選擇了神經網絡隱含層層數為2，單層神經元個數為527，隱含層激活函數為relu，權重優化算法為lbfgs的超參數組合建立分類模型。通過試驗驗證其分類準確率達到87.1%，遠高于現有組件信號識別方法的準確率75%,證明了本文提出的方法可以更好的識別組件信號和多余物信號，解決實際工程問題。

在后續的工作和研究中，可基于當前的研究工作對多層感知機的內部其他超參數選擇繼續研究，從而實現減少識別誤差、提高精度、降低運行時間、更為理想的分類效果等。還可以通過選用不同優化參數的算法組合，實現更加精準、更加快速確定最優解，最終實現分類器的優化。