紫外-可見連續光譜法對農村生活污水處理出水COD的在線監測方法

曲江北，李 彭，何義亮，王志平

(上海交通大學環境科學與工程學院，上海 200240)

隨著社會經濟的發展和人民生活水平的提高，人們越來越關注水環境狀況。在農村區域，生活污水的處理效率低且存在不達標排放現象，對環境的整潔和人體的健康都造成了巨大的危害。目前，農村開始普遍采用分散式處理的模式，并形成了污水處理設施規模小、位置分散、數量眾多的特點[1]。因此，需結合農村自身的經濟、環境狀況，尋求一種經濟、高效的水質實時在線監測方法來保障農村生活污水的達標排放。

化學需氧量(COD)，作為一項重要的水質檢測指標，能夠有效反映水體中有機物的總體污染水平。傳統的化學法檢測COD精度高，但存在反應時間長(0.5～4 h)、二次污染等問題[2]。此外，傳統化學法的COD檢測設備及樣品預處理設備昂貴、維護費用高，并不能有效適用于農村地區的污水實時在線監測。隨著光譜學的發展，包括紫外-可見光、三維熒光、近紅外光譜在內的光譜法分析技術不斷被應用于污水水質監測中[3-5]，其中，紫外-可見光譜的應用最為廣泛。相較于傳統的化學法，光譜法能夠實現對水質指標的快速檢測、無二次污染，且設備便宜，運行維護成本低。紫外-可見光譜最早的應用為UV254(254 nm波長下的吸光度)[6]以及后來的雙波長補償法[7]。隨著光譜數據的獲取變得更加便捷以及化學計量學的發展，紫外-可見光譜法開始被廣泛研究和應用[8],但對于紫外-可見光譜法COD監測模型的預測精確度和穩定性仍然有許多需提高的地方。

光譜法COD預測模型建模方法的選擇及光譜范圍的選擇是影響模型預測效果的最主要因素。目前，常用的預測模型構建方法包括多元線性回歸、偏最小二乘法、支持向量機、神經網絡等。Qin 等[9]認為,類似于偏最小二乘法的傳統統計學方法可以滿足光譜法水質模型的建模需求。而Lepot等[8]發現，偏最小二乘法和支持向量機在模型自身的校準方面更優，線性回歸、神經網絡算法則更適合模型預測。因此，目前還沒有一種公認的方法用于模型的構建。光譜法水質監測模型是基于COD濃度與不同光譜范圍下，水樣中有機物的吸收強度之間的線性相關關系，對于含有不同物質組分的水樣而言，紫外-可見光譜圖的吸收峰也不同。因此，光譜范圍的選擇會對模型運算的速率以及預測結果的精確度產生一定程度的影響。

近年來，紫外-可見光譜法已經被許多學者、工程技術人員[10-11]廣泛應用于水質指標的在線、原位監測。但對光譜法的研究具有局限性，缺乏對光譜法進行系統性的研究、優化，且研究對象大部分為實驗室配水而非實際污水。本文以實際農村生活污水處理設施出水為研究對象，從單波長法、雙波長補償法、紫外-可見光譜法逐步驗證光譜法水質COD預測模型的可行性，并通過對紫外-可見光譜的預處理、建模方法的比較選擇、特征波長篩選等手段對紫外-可見光譜法進行系統性優化改良，從而提出一套有效的紫外-可見光譜法COD預測模型的優化方法。

1 試驗部分

1.1 數據采集及光譜預處理方法

數據采集地點為江蘇省常熟市，為保證水樣均具有代表性，水樣采集地點分布于常熟市的所有農村區域，采集時間為2019年3月10日，所采集水樣分別來自110個分散式農村生活污水處理裝置的出水，共計110個樣品。水樣的采集與貯存均使用500 mL聚乙烯瓶，4 ℃保存。所有水樣進行分析前，均需通過0.45 μm的濾膜進行過濾。樣品COD的濃度參照國標GB 11914—1989重鉻酸鉀回流法進行測定。CODCr的質量濃度為20～200 mg/L。水樣中其余各項水質指標：溫度為17～18 ℃，pH值為6.6～7.5，溶解氧為7.5～9.5 mg/L，渾濁度為5～15 NTU，硝態氮為5～30 mg/L，氨氮為1.12～15 mg/L。

水樣的紫外-可見光譜由HACH DR/6000光譜儀掃描獲取，光譜選擇200～700 nm，間隔為1 nm。紫外-可見光譜預處理方法選用S-G平滑處理(savitzky-golay smoothing)、多元散射矯正(multiplicative scatter correction)、標準正態變換(standard normal variate transform，SNV)。

1.2 建模方法及模型評價參數

紫外-可見光譜法水質監測模型構建方法分別選用偏最小二乘法(partial least squares regression)、支持向量機(support vector machine，SVM)和神經網絡算法(back-propagation neural network method)。

紫外-可見光譜法水質監測模型的預測效果由均方根誤差(root-mean square error, RMSE)和決定系數(R2)來評價。均方根誤差(亦稱標準誤差)是預測值與真實值差的平方和與觀測次數n比值的平方根。R2表示可根據自變量的變異來解釋因變量的變異部分，當R2越接近1時，模型預測結果參考價值越高。

1.3 特征波長篩選方法

紫外-可見光譜特征波段的篩選采用間隔偏最小二乘法(interval partial least-squares regression, iPLSR)和組合間隔偏最小二乘法(synergy interval partial least-squares regression, siPLSR)相結合。2種方法均是將光譜數據等分成若干區間，再將不同區間相互組合構建模型，最終依據R2和RMSE篩選出最佳波段組合。在得到的最優波段中，利用套索回歸 (lasso regression)及逐步回歸法(stepwise regression)篩選出特征波長。

2 結果與討論

2.1 單波長及雙波長COD預測模型

大部分有機物在紫外光區域具有良好的吸收特性，且有機物濃度通常和254 nm波長下的吸光度(UV254)具有一定的線性關系，因此，UV254經常被用于衡量樣品中有機物的濃度[12]。如圖1所示，分別用實驗室配置的鄰苯二甲酸氫鉀溶液和采集的水樣構建COD-UV254線性回歸模型，相關性系數R2分別為0.997和0.821，說明無論在單一物質組分水樣中還是在實際污水中，UV254和COD濃度都能呈現良好的線性關系。因此，可以通過UV254的變化有效反映COD濃度的變化。

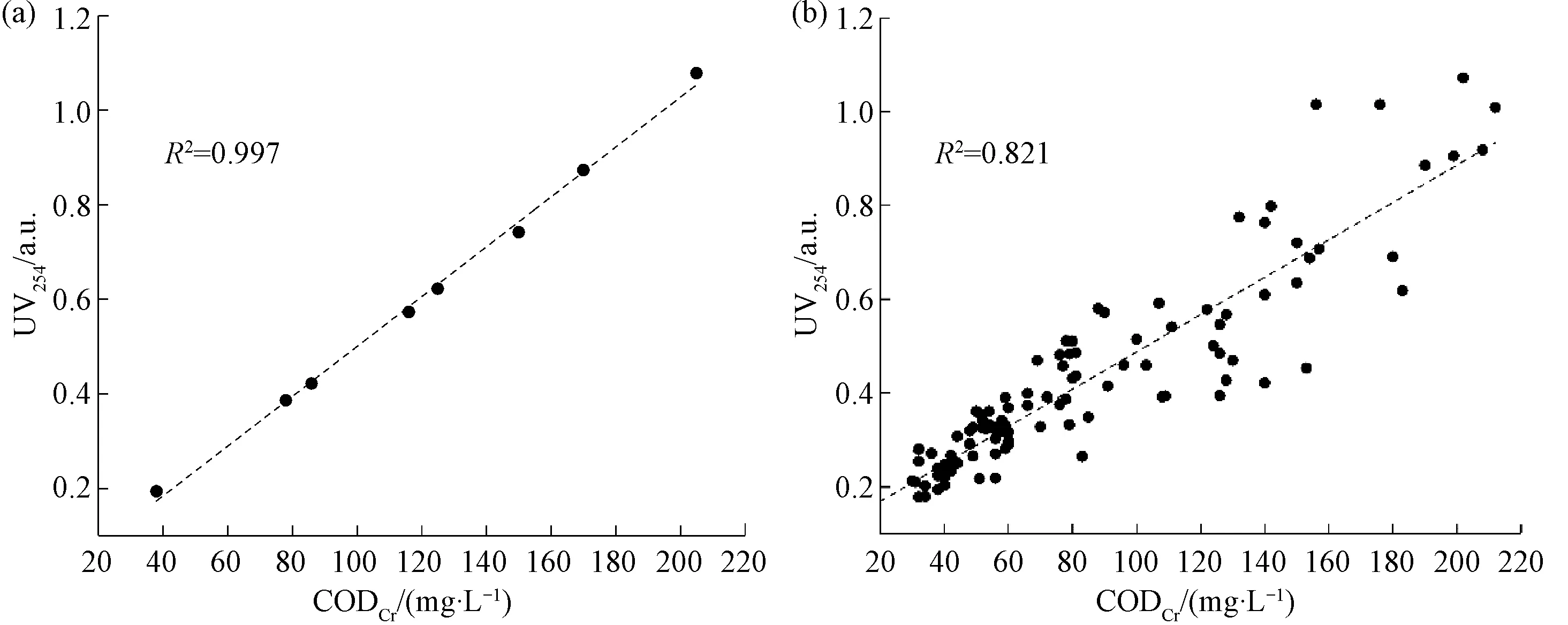
圖1 COD與UV254關系圖 (a)鄰苯二甲酸氫鉀溶液； (b)采集的水樣Fig.1 Correlation between UV254 and COD (a) Potassium Hydrogen Phthalate Solution; (b) Collected Water Samples

水中的某些物質，如懸浮態無機顆粒物等，對COD沒有貢獻但對光譜有一定的影響，因此，需考慮規避這類因素，提高光譜數據與COD之間的相關性。蔣然等[13]利用440 nm和560 nm的雙波長光譜法測定低污染水樣的COD時發現，相比于單波長的檢測方法，該方法檢測具有更高的靈敏度和準確性。趙友全等[14]通過254 nm處的紫外吸光度檢測水質COD，并采用546 nm可見光對渾濁度進行修正，預測R2均超過0.9。如圖2所示，利用水樣在546 nm下的吸光度對UV254進行修正，將546 nm的吸光度與UV254之間的差值作為修正后的UV254，并與COD構建線性回歸模型，得到的模型相關系數R2為0.856，相較于單波長模型，提高了模型的精確度。

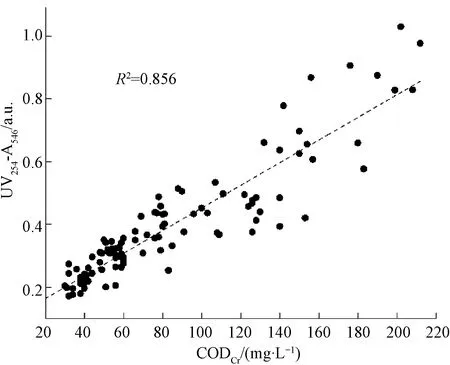
圖2 COD與UV254-A546關系圖Fig.2 Correlation between UV254-A546 and COD

通過單波長及雙波長補償模型的評價分析，2種模型雖然能夠實現COD濃度值的預測，但預測精度并不高，這是由于不同物質組分構成的水樣其特征吸收波長是不同的。單波長模型依據主要組分在某一波長下的吸光度來構建模型；而對于構建雙波長補償法，也可以采用不同的波長進行補償，其效果也不同，如湯斌等[15]研究了溶液分別在245、300、360 nm和560 nm處渾濁度對紫外-可見吸收光譜法檢測水質COD的影響。

有限波長數下的吸收光譜反映的水質情況也是有限的。雖然單波長、多波長水質COD預測模型在預測精確度方面存在一定的不足，但證明了光譜法水質COD預測模型的可行性，并為光譜法后續的研究及應用打下了堅實的基礎。

2.2 紫外-可見光譜預處理方法的選擇

由于實際水樣的成分更復雜，收集的紫外-可見吸收光譜可能會受到水體中復雜成分的影響，例如背景噪聲的干擾和渾濁度散射。因此，在進行光譜數據建模之前，需對光譜數據進行有效的預處理，分別采用S-G平滑處理、多元散射矯正、標準正態變換對紫外-可見光譜數據進行預處理。利用偏最小二乘法對原始光譜數據以及3種預處理光譜數據分別構建模型，對模型預測效果的評價，如表1所示。

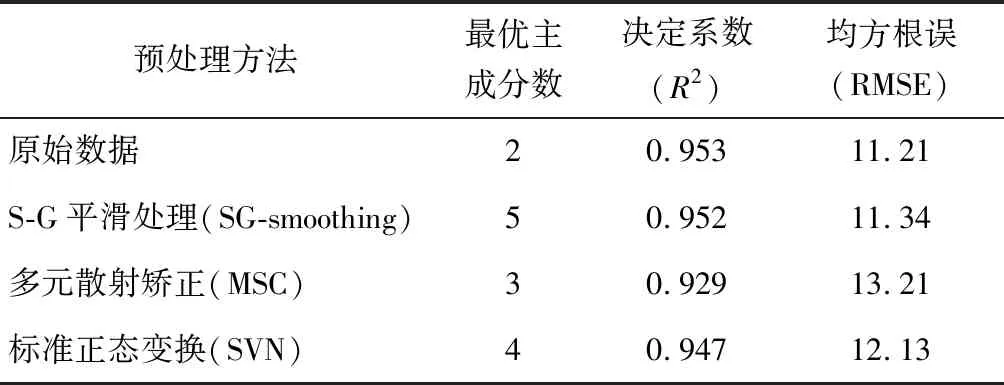
表1 不同預處理方法后的模型評價結果Tab.1 Results of Models Evaluation after Different Pretreatment

通過對比原始光譜和預處理光譜模型的評價結果發現，以上3種常用于光譜預處理的方法并沒有顯著提高模型的預測效果。紫外-可見光譜受干擾的因素主要包括水樣水質以及監測環境和設備。由于所研究水樣的渾濁度較低，并未對光譜產生較大的影響，無需采用預處理方法對光譜進行修正，此外，光譜測試技術的快速發展保證了光譜數據監測的可靠性及穩定性。因此，在光譜法水質COD監測的實際使用中，若水樣的渾濁度并未對光譜產生較大影響，選擇原始光譜數據即可滿足光譜法預測模型的構建。

2.3 建模方法的比較選擇

借助Python的Random函數從110個水樣中隨機挑選70%的水樣作為訓練集，剩余30%的水樣作為驗證集，分別利用偏最小二乘法、支持向量機、BP-神經網絡3種算法對70%水樣的原始光譜數據及COD構建預測模型，剩余30%水樣作為測試集對模型的預測效果進行驗證。如表2所示，依據R2和RMSE來評價3種模型的預測效果。

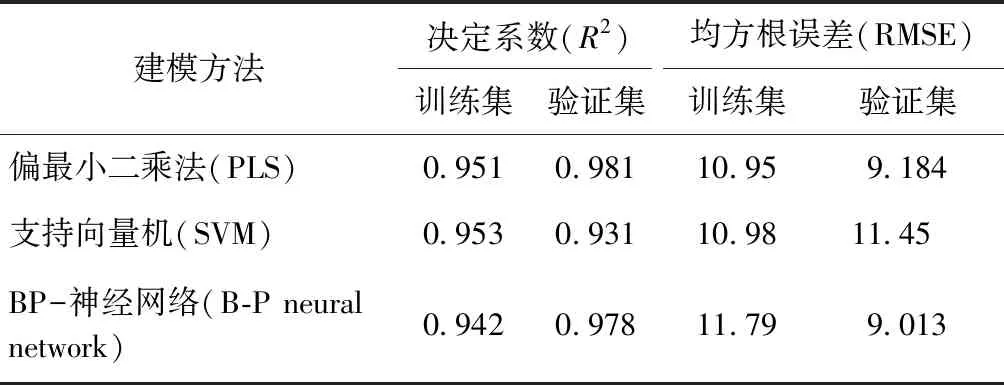
表2 不同建模方法的模型評價效果Tab.2 Evaluation Results of Models Constructed by Different Modeling Methods

由表2可知：在預測模型自身的構建方面，偏最小二乘法～支持向量機>BP-神經網絡；從模型的預測效果來看，偏最小二乘法～BP-神經網絡>支持向量機。光譜法預測模型建模方法的選擇不僅依賴于模型預測結果的精確度和穩定性，同時，也要考慮到建模方法本身的簡易程度及現實的技術條件。Lepot等[8]通過對不同建模方法的對比發現，偏最小二乘法和支持向量機在模型自身的校準方面更優，而線性回歸、神經網絡算法擁有更好的模型預測效果。Brito等[16]也在研究中指出，偏最小二乘法所構建的模型可以滿足需求，并不需要更加復雜的算法來構建模型。但是，如果水樣中的組分比較復雜或是光譜獲取的過程中存在許多干擾，如濁度散射等，光譜數據和COD濃度之間并不能始終保持線性關系，朗伯-比爾定律便會失效，偏最小二乘法也就不適合。對于B-P神經網絡算法而言，其既可用于構建線性模型也可用于構建非線性模型，但是，神經網絡算法需更多的水樣數據來構建模型。隨著在線監測技術的不斷發展，大量水樣指標數據的獲取將變得更加容易，神經網絡算法也將會發揮自身的優勢，不斷提高光譜法預測模型的預測精度。

建模方法的選擇不僅取決于模型的預測效果，同時，也要考慮建模的復雜度及成本。對于農村污水處理設施出水而言，偏最小二乘法最為合適。對于不同類型的水樣，同樣需要從各個方面進行考量，選擇一種最為合適的建模方法。相信隨著光譜法的不斷發展及化學計量學的不斷深入研究，一種具有普適性的建模方法將會被提出，并廣泛應用于光譜法水質監測模型。

2.4 特征波長篩選

不同物質在某一波長下的吸光度有所不同，因此，對于不同物質組分的水樣而言，其特征波長也有所不同。由圖3可知，隨著波長的增加，吸光度的變化會越來越小。當波長大于450 nm時，即使水樣COD濃度不同，吸光度也并沒有明顯的變化，說明COD濃度的變化并不會對某些波長下的吸光度產生影響。因此，在建模的過程中，僅利用含有水質信息的光譜數據進行建模，不僅可以提高建模效率，還能夠降低光譜測量工作量。

將A組水樣的光譜數據(200～700 nm下的吸光強度)根據波段進行30等分。利用iPLSR 和siPLSR對30個波段的吸光強度和COD進行不同組合數的模型構建，并根據模型評價參數R2和RMSE從所有所建模型中篩選出最優的波段組合(圖4)。

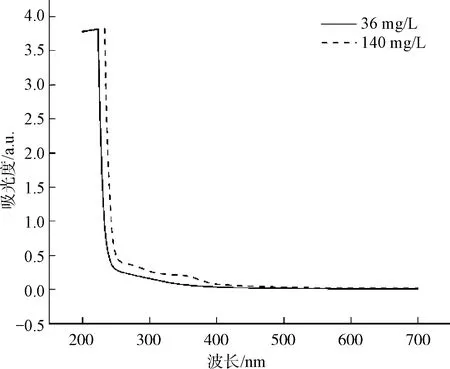
圖3 不同COD濃度的水樣光譜圖Fig.3 UV-Visible Absorbance Spectra of Two Samples with Different COD

圖4 不同波段篩選組合模型評價結果Fig.4 Evaluation Results of Models Constructed by Different Bands Selected Region Combination

由圖4可知，三波段組合的模型預測效果最佳，對應的最優波段分別為251～268、319～336 nm和353～370 nm，且均在近紫外區。一般的飽和有機化合物在近紫外線區域沒有吸收，而含有共軛雙鍵或苯環的有機化合物在紫外線區域具有明顯的吸收或特征峰，這也證實了光譜法適用于含有共軛雙鍵或苯環水樣品的有機化合物。此外，相較于全光譜模型，特征波段篩選幾乎沒有影響到模型的預測效果，反而減少了模型的運算量，提高了效率。

通過對比相鄰波長下的吸光度發現，鄰近波長下的吸光度之間存在較強的相關性，R2高達0.95以上。這也為再次減小波長數提供了依據，即可以通過某一波長替代其鄰近的波長。利用套索回歸對三波段組合進行最優波長篩選，篩選結果為251、356、357、362 nm和363 nm，再利用逐步回歸法對5個波長進行變量篩選，得到的最小信息準則(AIC)為118.36，篩選出的特征波長為251、356 nm和363 nm。由圖3可知，這3個波長下的吸光強度也是紫外-可見吸收光譜中局部區域的峰值，可以有效反映水樣中含有芳香環結構或共軛雙鍵物質的有機物含量。

根據波長篩選得到的3個波長下的吸光度與COD構建多元線性回歸模型(MLR)。如圖5所示，與全光譜模型(表2)相比，R2和RMSE僅僅發生了微小的變化，全光譜法適用于水樣水質的精確監測。而特征波長的篩選應用不僅可以有效降低測試成本及檢測工作量，更重要的是依然可以保證模型的預測效果。該方法適用于對水質預測精度要求較低的場景或用于水質預警，對于紫外-可見光譜法監測水質COD的進一步發展與實際應用提供了一種新的思路。

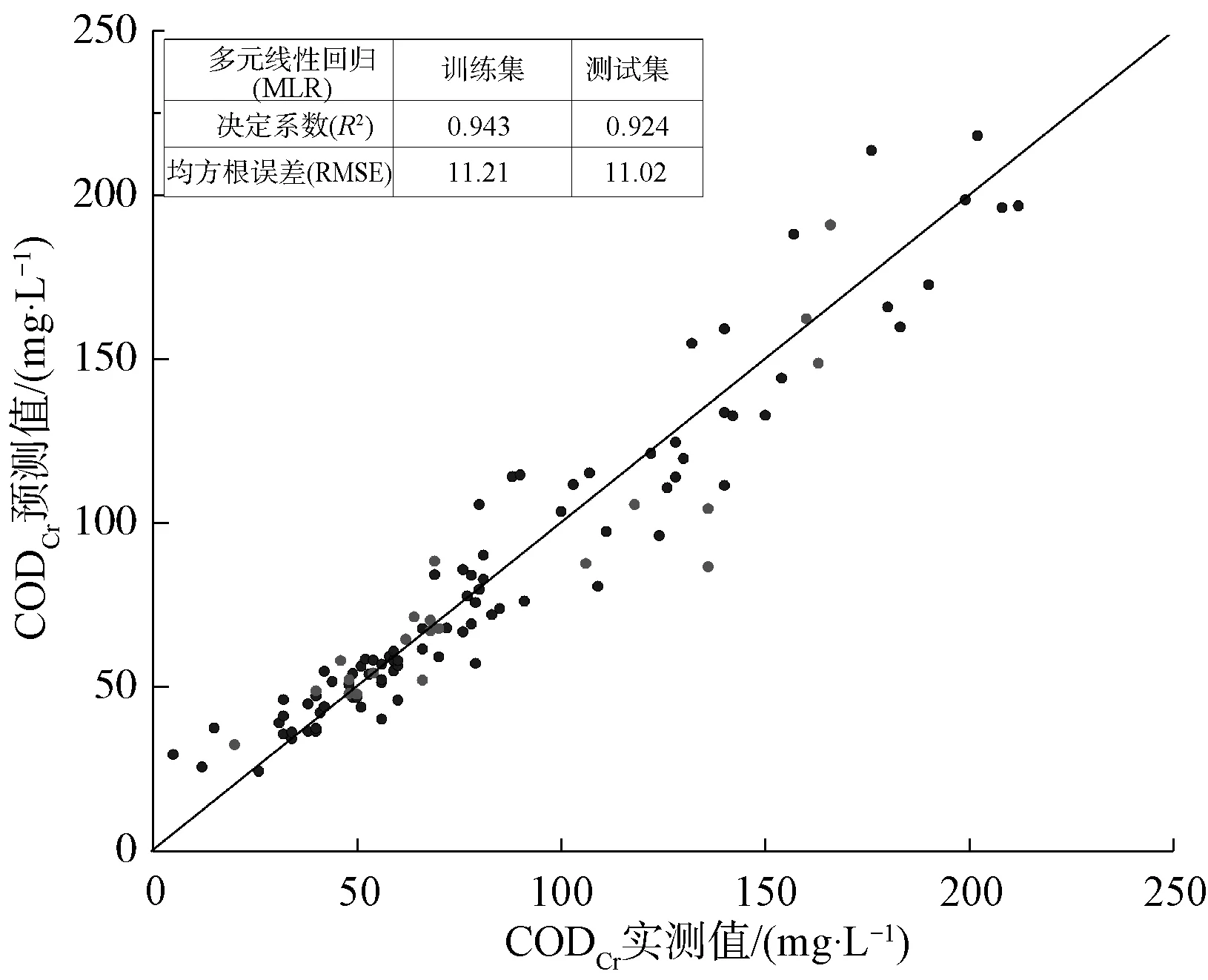
圖5 實際污水COD濃度值與模型預測COD濃度值多元線性擬合關系圖 (比例為 1∶1)Fig.5 MLR Fitting Relationship of Practical and Model Prediction COD Values (Ratio is 1∶1)

3 結論

本文以實際的農村生活污水生物處理設施出水為研究對象，驗證了光譜法進行污水水質COD指標檢測的可行性，并對光譜法水質COD預測模型進行系統性優化。

(1)光譜數據無需預處理即可滿足光譜法水質預測模型的構建需求。

(2)從模型運算復雜度及精度考慮，偏最小二乘法是最適合的建模方法，模型相關系數R2為0.949，均方根誤差RMSE為11.03。

(3)波長篩選可以在保證模型精度的前提下簡化建模過程，最優波長的篩選結果為251、356 nm和363 nm，所構建的模型R2為0.943。

以上對光譜法水質COD預測模型的優化改良方法并不局限于農村生活污水處理設施出水，對于不同類型污水的光譜法COD預測模型的優化同樣具有參考價值，為光譜法在實際污水監測領域中的發展和應用提供了一種新的思路。