GF(2m)域ECC 點乘算法優化設計*
劉金龍,張玉婷,王 堯
(海軍參謀部,北京 100841)
0 引言
無線傳感器網絡(Wireless Sensor Network,WSN)是由一種分布式、自組織的Ad hoc 網絡,但有別于傳統的Wireless Ad hoc 網絡。WSN 節點由能量有限、計算和存儲能力小、具有數據采集功能的傳感器節點組成。隨著傳感器節點資源的升級和某些傳感器網絡應用的高強度安全需求,非對稱加密算法已被廣泛研究[1]。橢圓曲線密碼算法(Elliptic Curves Cryptography,ECC)因為自身的安全強度高、密鑰長度短、存儲和帶寬要求低等優點[2],特別適用于WSN 等資源受限的領域。而在ECC 密碼體制中,橢圓曲線的點乘運算(Q=kP)是算法安全性的關鍵,占了整個運算的很大比例,決定了算法的執行效率[3]。因此,研究有限域內點乘運算的優化實現具有重要的意義。
考慮到硬件實現的特點,本文以二進制域的橢圓曲線密碼方案為研究重點,在權衡資源消耗與運算速度的基礎上,設計了串并混合的點乘運算整體結構,并實現底層有限域的模加、模乘、模平方和模逆運算的輕量化改進和電路結構設計,最后在FPGA 平臺上進行仿真驗證。結果表明,方案的點乘運算效率得到了明顯提升。
1 橢圓曲線密碼基礎
1.1 橢圓曲線的定義
定義在二進制域GF(2m)的橢圓曲線可表示如下:

其中a,b∈GF(2m),且b≠0,除了式(1)所確定的所有點(X,Y)外,還包括一個特殊的點即無窮遠點。在實際應用中,為避免一些復雜的運算,橢圓曲線上的點通常用其他坐標系表示[4]。在標準射影坐標下的點可表示為(X,Y,Z),Z=0 表示無窮遠點,Z≠0 時相互之間的轉化關系為x=X/Z、y=Y/Z。
1.2 橢圓曲線上點的運算
橢圓曲線上所有的點的集合外加上無窮遠點和橢圓曲線上的加法運算構成一個加法群[5]。在GF(2m)域內,令E為式(1)所表示的曲線,P=(x1,y1),Q=(x2,y2) ∈E,R=(x3,y3)=P+Q,則P、Q兩點相加的運算規則如下。
(1)當P≠Q時,點加運算:
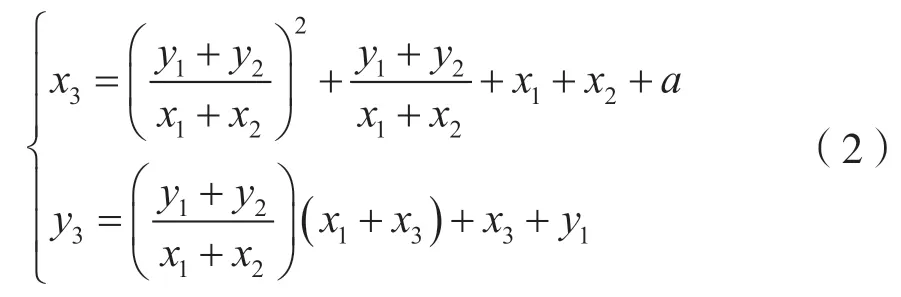
(2)當P≠Q時,點加變為倍點運算:
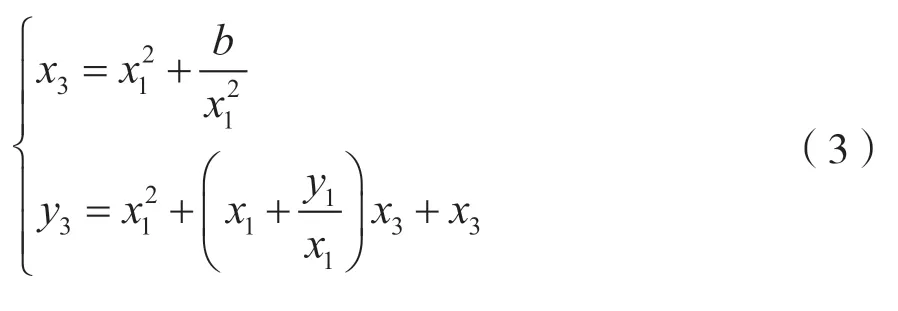
1.3 橢圓曲線密碼體制的運算層次
點乘運算在橢圓曲線加密體制中的作用如圖1 所示。最上層為協議層,通過調用點乘運算實現ECC 加解密和數字簽名;之后為群運算層,通過調用點加和倍點運算實現點乘運算;最底層為域運算層,包括多種有限域模運算,是實現點加和倍點運算的基礎[6]。因此,實現橢圓曲線點乘運算的高效設計需要針對不同運算層次的特點進行針對的優化設計。
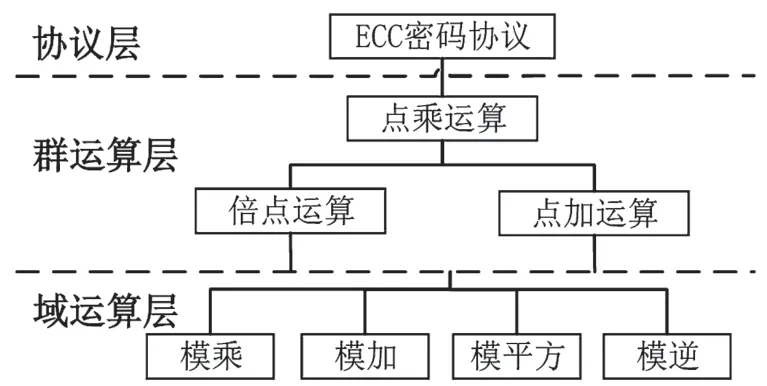
圖1 橢圓曲線加密體制的運算層次
2 有限域模運算優化設計
有限域內的模運算是點乘運算實現的基礎,是影響點乘運算效率的關鍵。下文分別對GF(2m)域上的模加運算、模平方運算、模乘運算和模逆運算進行優化設計。
2.1 模加運算設計
有限域GF(2m)域內的加法相對簡單,可以通過將表示模加元素的二進制序列進行逐位異或運算來完成。
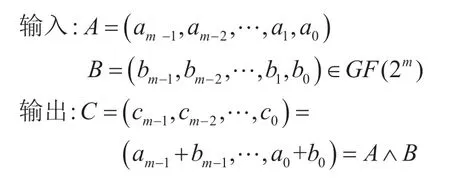
它對應的硬件電路可用m個異或門實現,如圖2 所示。
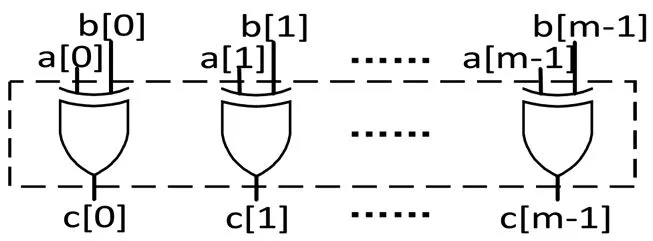
圖2 模加單元電路結構
2.2 模乘運算設計
模乘運算是影響點乘實現效率的關鍵,包括多項式相乘和取模兩步,而多項式相乘部分的計算周期較長,分為并行和串行兩種類型。有限域GF(2m)并行結構乘法器的硬件復雜度為m2,它的面積和功耗隨m的增加而增加。在硬件實現時常用串行模乘算法,雖然該算法的計算周期較長,但是其實現面積和功耗最小[7],比較適合無線傳感器網絡這種資源受限的環境。本文采用一種優化的LSB 串行模乘算法,如下:
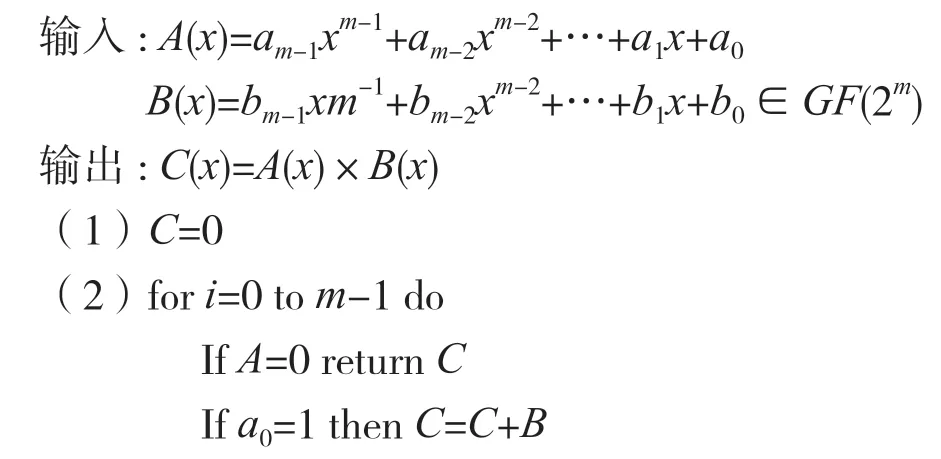
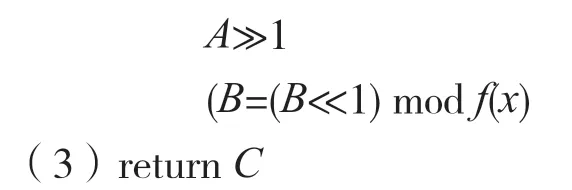
算法在每次循環中完成兩次異或和兩次移位操作,對于硬件實現來說很方便,而且不需要占用任何邏輯單元。通過對A的移位操作,通過A值是否為0 進行判斷,確定算法是否結束。當A的高位有多個0 時,算法的運算效率會顯著提高。另外,算法中的移位和判斷操作對算法的運算效率影響很小。
模乘單元的硬件電路結構如圖3 所示。
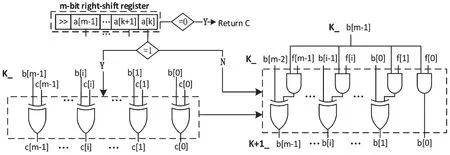
圖3 模乘單元電路結構
2.3 模平方運算設計
在有限域GF(2m)內,模平方運算可以用模乘來實現。但是,由上文可知,模乘運算的計算周期較長且硬件電路設計復雜。因此,本文利用有限域GF(2m)下模平方運算的特殊性,采用一種基于多項式平方的快速模約減算法,通過預計算的方式,犧牲算法的靈活性,達到提高計算的效率并減少資源消耗的目的。
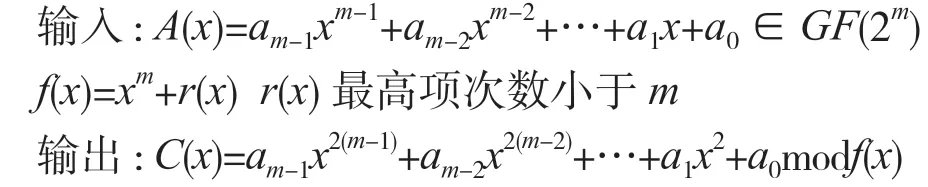
對約減多項式f(x)進行取模時,根據xm=r(x)modf(x),將A2(x)中次數高于m-1 的多項式元素轉化為低于m位,再把結果在同一位的所有值進行異或。在固定的約減多項式下,通過預計算,模平方運算可在一次異或運算時間內完成,且所用的資源不超過m個異或門。
針對特定的m≤233 與f(x)=x233+x47+1,對應的組合邏輯電路設計如圖4 所示。
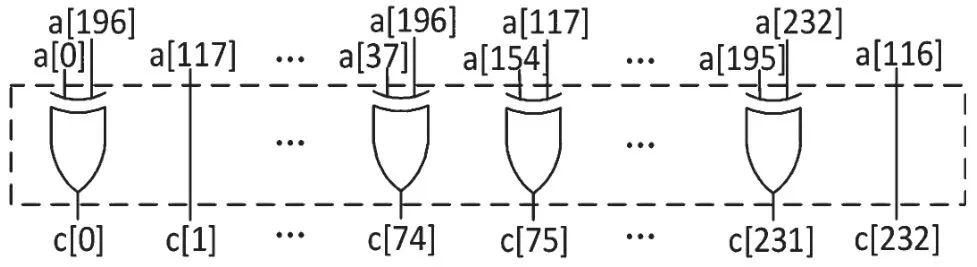
圖4 GF(2233)域下模平方單元結構
2.4 模逆運算設計
模逆運算是有限域運算中最復雜也是最耗時的。GF(2m)域上的求模逆算法有兩種——基于擴展Euclideam 算法和基于Fermat 小定理的算法[8]。前者通過判斷、移位和異或來實現模逆運算,實現比較簡單,但是需要增加單獨的模逆運算模塊,大大增加了整體面積;而基于Fermat 小定理的模逆算法是將有限域的逆運算轉換為模冪運算,可以通過調用模乘和模平方來實現,算法如下。
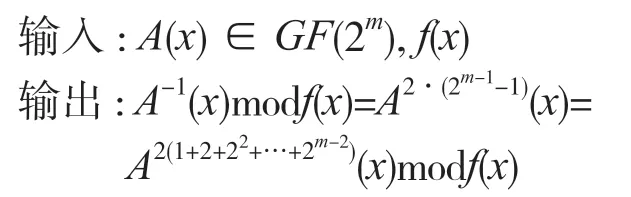
可以看出,一次模逆運算需要m-2 次模乘和m-1 次模平方。盡管這樣,一次模逆運算的計算效率還是較低。而由前文可知,模乘運算的計算復雜度比模平方復雜得多,本文采用Itoh-Tsujii 算法[9]改進運算,以減少模逆運算中的模乘運算次數。
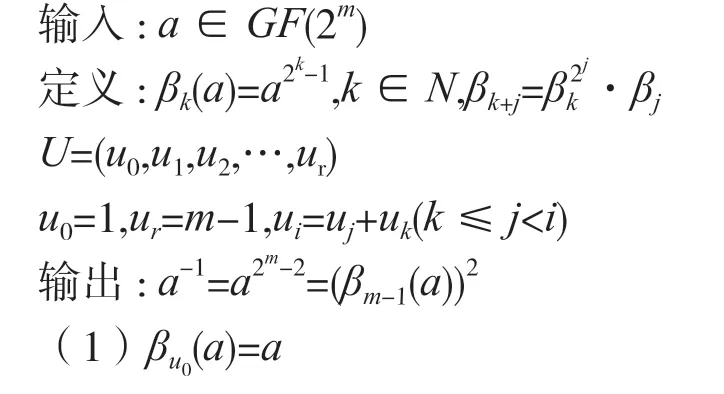
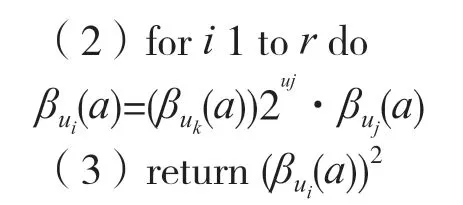
所以,當a∈GF(2233)時,可以得到加法鏈U=(1,2,3,6,7,14,28,29,58,116,232)。可以看到,求一次模逆運算僅需要10 次模乘和232 次模平方運算,具體的計算過程如表1 所示。由計算過程可知,每一步都具有相關性,只能串行執行。

表1 Itoh-Tsujii 模逆計算過程
在ECC算法中,模逆與乘法運算是分步進行的,因此可以將乘法器集成在模逆運算單元中,加上一個模冪運算單元組成乘/逆運算單元。其中,模冪運算可以利用一個計數器和一個模平方單元實現。具體的硬件結構如圖5 所示。
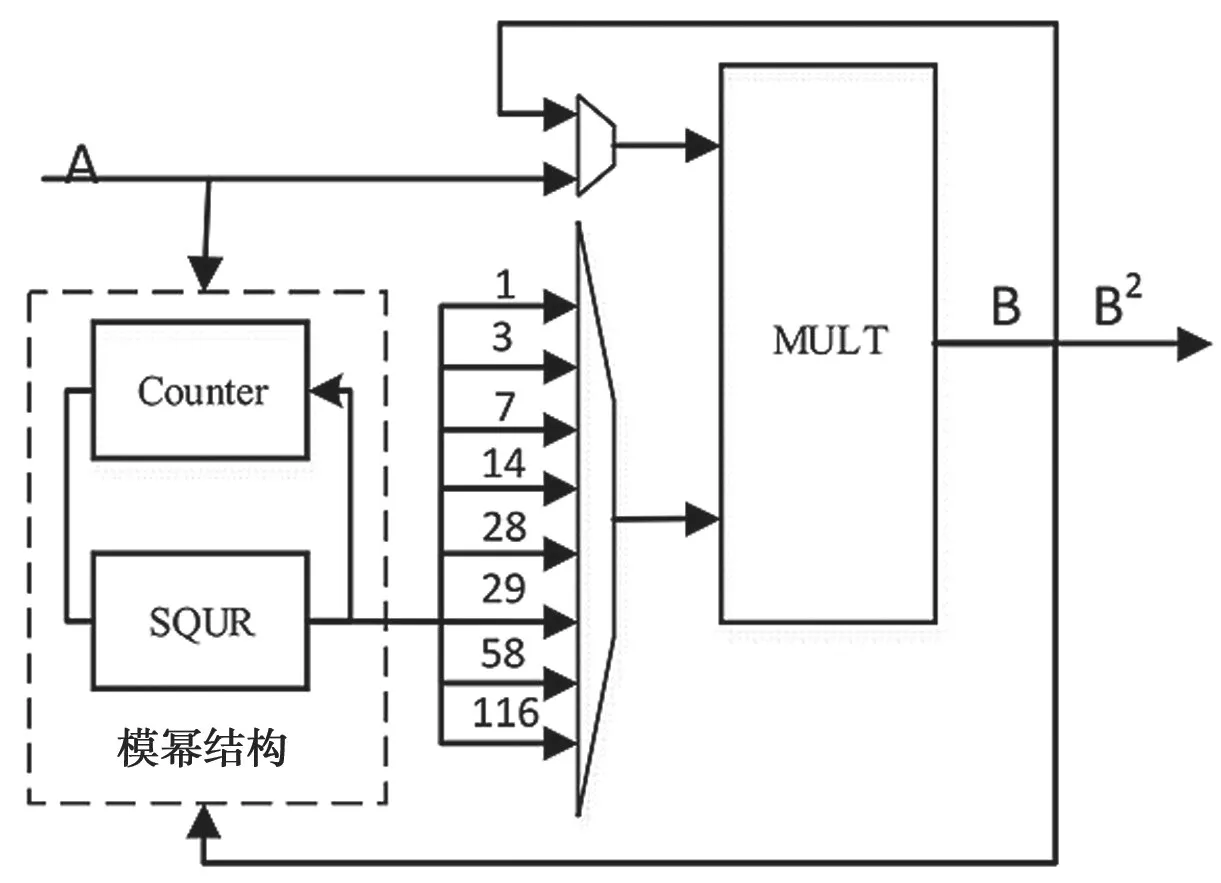
圖5 GF(2233)域模乘/逆單元結構
3 點乘運算總體方案設計
3.1 點乘算法分析與設計
ECC 點乘算法包括模加、模平方、模乘和模逆運算,其中模逆運算的運算復雜度是其他運算的數十倍[10]。在仿射坐標下計算點乘需要多次模逆運算,而在投影坐標下只需要一次模逆運算。為避免進行多次模逆運算,本文采用投影坐標下的Montgomery點乘算法[11]。Montgomery 算法是現階段最安全高效的點乘算法,相較于其他算法不需要進行預處理,且在計算過程中只用到點的橫坐標,特別適合在硬件上實現。投影坐標下的Montgomery 算法包括初始化、主循環和坐標轉換3 部分。

初始化部分主要實現對循環部分的輸入數據初始化處理,輸入投影坐標下點P(x0,y0),輸出投影坐標下點P1、P2,可以用兩個模平方模塊在1 個時鐘周期內完成。P(x0,1)為點P 在射影坐標下的對應點,P2為P1的2 倍點,可以利用一個倍點運算在3 個時鐘周期內實現。點加和倍點數據流分析,如圖6所示。
主循環部分由m-1 次點加和倍點運算組成。由于兩者之間沒有數據依賴關系,可以同時計算。通過對循環部分的數據流進行分析,可以看出每次循環中共執行6 次模乘、5 次模平方及3 次模加運算。本文采用整體串行部分并行的結構,利用兩個乘法器,將第i次循環中的點加和倍點運算(Montgomery算法中的①②(③④)步)劃分為3 個階段串行完成,每個階段中的運算并行執行。
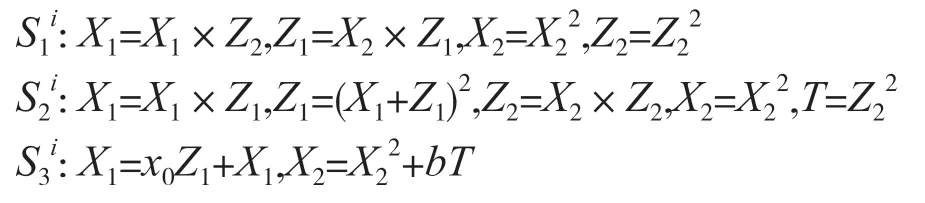
一次循環可以用2 個模乘模塊、2 個模加模塊和2 個模平方模塊在3 個時鐘周期內完成,因此整個主循環部分共需要3(m-1)個時鐘周期。
坐標轉換部分主要實現將投影坐標變換成仿射坐標,輸入投影坐標下點P1、P2,輸出仿射坐標下點Q(Qx,Qy)。主要計算過程為:
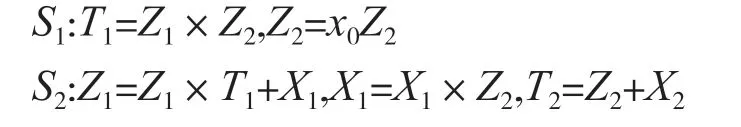
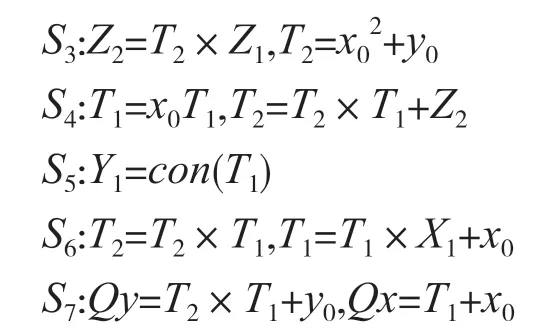
可見,它包括1 次模逆、10 次模乘、1 次模平方和7 次模加運算,可以用1 個乘法單元、1 個乘/逆單元、2 個加法單元和1 個平方單元在6+t個時鐘周期內實現,其中t為一次模逆運算的時間。
3.2 總體電路結構設計
點乘運算3 個部分的結構可以共用,整體的硬件電路實現如圖7 所示,共需要1 個模乘單元、1個模乘/逆單元、2 個模加單元和2 個模平方單元,共使用7 個寄存器X1、Z1、X2、Z2、T1、T2、R。其中,用來存儲曲線的參數值x0、y0、b,寄存器X1、Z1、X2、Z2用來存儲點乘算法中的坐標值,T1和T2寄存計算過程的中間值。
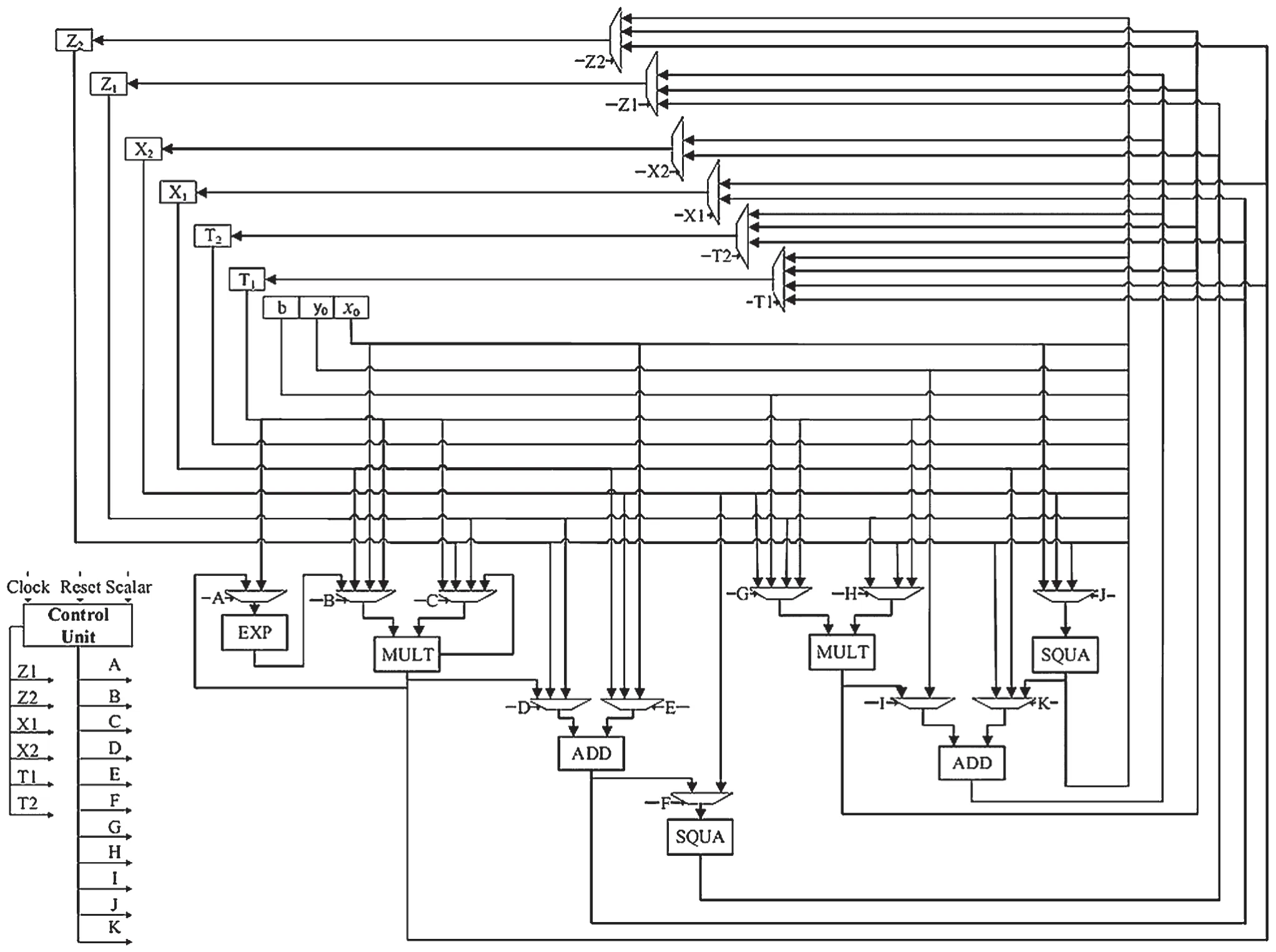
圖7 點乘總體電路結構
4 實驗結果分析
本文選用GF(2233)域上的Koblitz 曲線,y2+xy=x3+x2+1,對本文的點乘運算方案進行驗證。以Artix7 器件中的XC7A100T 為硬件平臺,利用Verilog 語言在FPGA 平臺上進行結果仿真驗證,并選用Modelsim 軟件進行波形分析。圖8 是本方案執行一次點乘運算的仿真結果。

圖8 仿真波形
根據本文設計的方案,在GF(2233)域內完成一次點乘運算共需要3+233×3+6+t個時鐘周期,其中t為一次逆運算的時間。在FPGA 上的仿真結果及與其他方案的對比如表2 所示,算法執行過程中占用10 682 個Slices 資源,共用時1.644 4 ms。
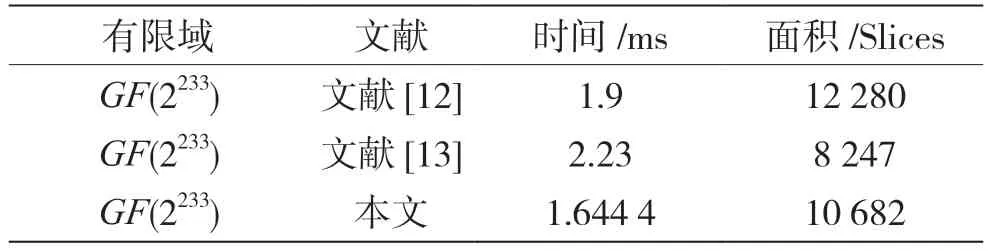
表2 測試結果及對比
通過與其他相關文獻的對比可以看出,本文設計的點乘計算方案在占用面積和計算時間上都有所提升。
5 結語
本文通過對ECC 密碼算法進行研究,針對不同運算層次的特點作了針對的優化改進,設計并實現了輕量化ECC 點乘計算方案。首,先通過對有限域的模運算單元進行研究,重點對模乘和模逆計算單元進行了改進;其次,根據Montgomery 點乘算法設計整體的計算流程,并以此為基礎實現了有限域運算單元和整體點乘方案的電路結構設計。本文方案采用整體串行部分并行,經過在FPGA 平臺上測試并與其他方案進行對比,達到了計算速度與占用面積的優化平衡,可以很好地適應于無線傳感器網絡等資源受限的場合。

