基于多目標約束三維水平井軌道優化設計研究

王六鵬, 魏 磊, 高云文， 張燕娜, 陳聯國， 張 明

(1西安石油大學石油工程學院 2中國石油渤海鉆探工程有限公司第二鉆井工程分公司>3中國石油長慶油田分公司油氣工藝研究院 4中國石油川慶鉆探工程有限公司長慶鉆井總公司)

三維水平井在薄層油氣藏、低滲透油氣藏等特殊油氣藏開發中具良好效果[1-4]。井眼軌道優化設計不僅可降低工程施工困難而且可進一步提高油藏開發效益。常規優化設計方法是給定地質靶點坐標要求設計軌道準確穿越靶點，然而由于靶點位置及工程條件的制約，往往難以尋找一條既滿足工程約束又準確入靶的最優軌道。目前國內外眾多學者提出了三維水平井井眼軌道優化設計模型[5-7]，龐明越等針對渤海油田建立了以井眼軌道長度最短為目標的“直—增—穩—邊增邊扭—水平段”型水平井軌道優化設計模型[8]，閆吉曾從基本公式和靶點約束方程出發，推導了軌道參數計算公式，建立了“直—增—扭—穩—增—平”的三維水平井軌道設計[9]。胥豪等人建立了以靶點為等式約束的六段制三維水平井優化設計模型[10]。李偉等人針對涪陵地區頁巖氣田三維水平井的特點，建立了七段式軌道優化設計模型，通過井斜角方位角組合，確定最短井深的優化軌道[11]。雖然眾多學者對三維井眼軌道設計展開深入研究，但是往往難以尋找一條既滿足工程約束又準確入靶的最優軌跡，實際設計時是通常為調整靶點坐標后重新設計，需耗費大量人力及計算工作。

針對這一問題，本文將給定地質靶點坐標與設計軌道入靶點坐標差的平方和定義為入靶精度，認為設計軌道滿足給定入靶精度即為有效，提出滿足入靶精度條件下最優井眼軌道設計思路。以入靶精度及最短設計井深作為雙優化目標函數，以造斜段造斜率和扭方位段全角變化率作為工程約束，以“直—增—穩—增扭—穩—水平段”五段制三維水平井軌道作為設計剖面，建立基于多目標約束三維水平井軌道優化設計模型，并應用該模型對實鉆井眼軌道進行了優化設計，可在滿足要求條件下減少水平井眼軌道長度，能夠有效指導井眼軌道優化設計工作。

一、三維軌道優化設計模型的建立

1. 設計思路

水平井軌道設計的難點之一在于要求井眼位置不僅進入目標窗口，而且井眼方向要與目標段設計方向一致[12]。“直—增—穩—增扭—穩—水平段”五段制三維水平井軌道優化設計如圖1所示，當給定地質首靶點T、末靶點T′坐標參數后，水平段井眼軌道方向可由TT′唯一確定。當給定首靶點T處的入靶精度為e(e≥0)時，此時水平段入靶范圍為以T點為圓心、e為半徑的空間圓，而水平段靶體為由T±e和T′±e所構成的空間圓柱體。此時，在滿足工程約束條件下的水平段穿越該空間圓柱體并與其方向一致的井眼軌道即為有效井眼軌道，而此時滿足這一條件并具有最短井深三維水平井眼軌道即為最優。

圖1 五段制三維水平井軌道優化設計示意圖

圖1中，水平段長為首靶點和末靶點線段TT′長度，水平段方向可用T點的井斜角和方位角為αT、φT表示。OA為垂直段，A點為造斜點，其垂深為HA；AB段為造斜段，造斜半徑以R1表示，造斜末點B處的井斜角和方位角為αB、φB；BC段為造斜后穩斜段，長度為LBC；CD段為增斜扭方位段，為一空間斜面圓弧，該空間斜面圓弧的半徑用R2表示，增斜扭方位末點D處的井斜角、方位角與首靶點T處的井斜角、方位角相同；DT為增斜扭方位后穩斜段，長度為LDT。

1.1 已知定靶點坐標時水平段方向的計算

在井眼軌道設計之前，根據地質給定井口坐標，首靶點及末靶點坐標參數，計算出水平段方向，可用首靶點T處的井斜角及井斜方位角表示，如式(1)、式(2)所示[13-14]。

(1)

(2)

式中：NT、ET、HT、NT′、ET′、HT′—分別為首靶點T和末靶點T′的北、東和垂深坐標，m；αT、φT—首靶點T處的井斜角、方位角，°。

1.2 已知造斜率時造斜半徑的計算

造斜段或增斜扭方位段造斜斜面圓弧半徑依據造斜工具造斜率來確定，當給定造斜率時計算公式如式(3)：

(3)

式中：R—造斜半徑，m；K—給定造斜工具造斜率，°/30 m。

1.3 待優化設計參數

在本文建立的“直—增—穩—增扭—穩—水平段”五段制水平井軌道優化設計中，已知參數有：井口坐標及首靶點T、末靶點T′坐標參數。待優化設計參數有：造斜點垂直深HA；增斜段造斜率K1；增斜段末井斜角、方位角αB、φB；造斜后穩斜段長度LBC，增斜扭方位段狗腿度K2，增斜扭方位段后穩斜段長度LDT。當這些未知參數確定后，可唯一確定一條五段制三維水平井設計軌道。

2. 優化設計模型

為了便于計算，待優化設計參數記為x1=HA、x2=R1、x3=αB、x4=φB、x5=LBC、x6=R2、x7=LDT。針對“直—增—穩—增扭—穩—水平段”五段制三維水平軌道，分別建立以最小入靶精度和最短井深雙目標函數的最優化軌道設計模型，如式(4)所示。

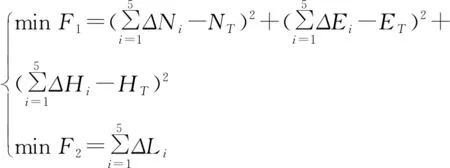
(4)

在式(4)中，第一優化目標函數F1為最小入靶精度，第二優化目標函數F2為最短井深。顯然，目標函數F1在無約束條件下極小值為0，而滿足次條件的最優解為準確穿越首靶點T的設計軌道，然而在三維軌道優化設計中存在實際工程約束，此時難以找到滿足目標函數F1極小值。

因此給定入靶精度為e(e≥0)后放寬目標函數F1極小值位于F1≤e范圍內，此時最優解為由|X1*| +ε所構成的鄰域范圍，在該鄰域范圍應用優化目標函數F2即可得到最短軌道長度。每段軌道的坐標參數及井深計算見式(5)～式(9)。

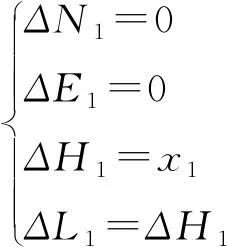
(5)

(6)

(7)

(9)

其中，所有未知參數為不等式約束，取值范圍可根據工程實際約束條件或工程經驗確定，如(10)式所示：

(10)

3. 優化設計模型的求解

本文所提出的三維軌道優化設計模型為多目標優化問題[15]，此類多目標優化問題的數學模型為[16]：

min[F1(X),…,Fi(X)] (i≥2)

(11)

s.t.Xmin≤X≤Xmax

式中：X=(x1,x2,…,x7)—待優化設計變量；

Fi(X)—按照重要程度從高到低排列的優化目標函數，其中約束為待求解變量的上下限方程。

寬容分層法是求解多目標優化的有效方法之一，該方法的主要求解思想是將上一步最優解進行寬容后再代入到下一步優化求解，逐步求解每個目標函數最優解最終求得滿足所有目標函數的最優解。

第一步，將目標函數F1的極小值用給定的入靶精度e(e≥0)擴大后優化求解，此時最優化方程如式(12)所示。

(12)

s.t.Xmin≤X≤Xmax

求解式(12)，得到的最優目標函數為F1*≤e，最優解為由|X*|+ε所構成的鄰域范圍。

第二步，根據第一步求出的最優解鄰域來定義優化目標函數F2的定義域，即：

(13)

s.t.X*-ε≤X≤X*+ε

二、實例驗證及分析

針對文獻[2]中的渤海油田F30H井參數采用本文提出的“直-增-扭-穩-增-平”進行三維水平井優化設計。已知首靶點T的坐標參數為NT=84.84 m，ET=1 212.57 m，HT=1 510.95 m，末靶點T′的坐標參數為NT′=-141.14 m，ET′=1 626.58 m，HT′=1 509.97 m；計算出首靶點井斜角和方位角分別為αT=90.12°、φT=118.52°；給定入靶精度e為0.5 m。

根據工程條件，給定增斜段造斜率K1為(2°～4°)/30 m；增斜扭方位段狗腿度K2為(2°～3°)/30 m；依據工程經驗，給定造斜點垂深范圍為100～200 m；造斜末點B井斜角和方位角范圍分別為0～100°、0～360°；兩段穩斜段長度范圍為0～2 000 m。

應用優化方法求解后，得到優化設計結果為：HA=130 m、K1=3.368°/30 m、αB=37.23°、φB=73.2°、LBC=968.5 m、R2=2.885°/30 m、LDT=0 m，實際入靶精度e=0.3085 m，最優井眼軌道長度為2 576.49 m。優化的結果見表1。

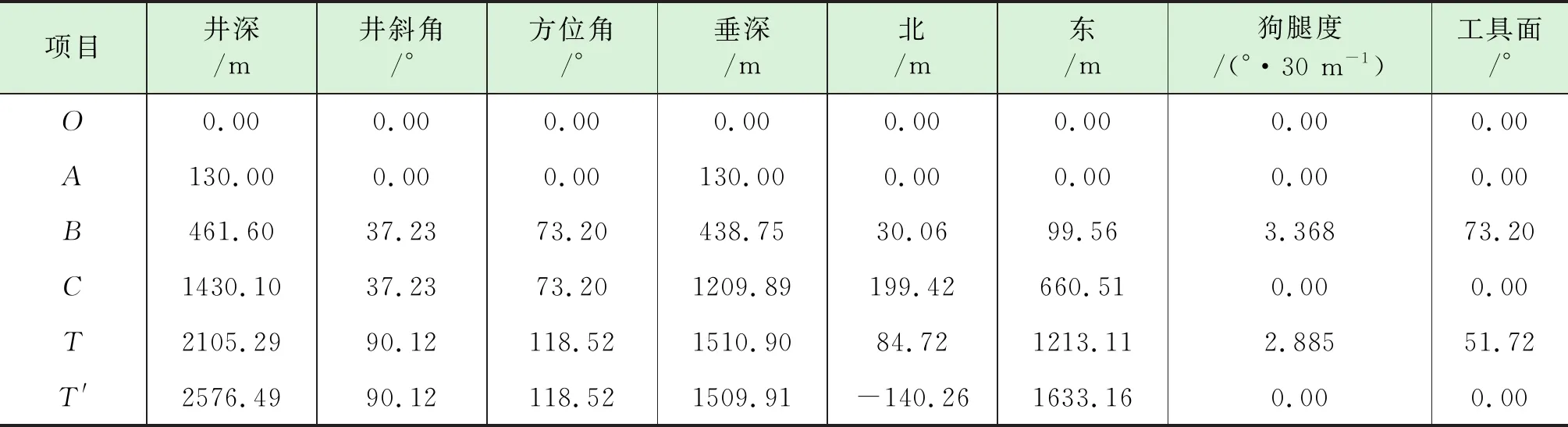
表1 三維水平井軌道剖面優化結果數據表

與文獻[2]結果對比可知，最短井眼長度兩者相差不大。文獻中造斜段AB的造斜率及扭方位段CT的狗腿度分別為3°/30 m和2.95°/30 m，本文計算出的造斜率及狗腿度分別為3.368°/30 m和2.885°/30 m，本文最優井眼軌道在入靶前的扭方位段具有更小的造斜率，利于施工作業。

三、結論

(1)針對“直-增-穩-增扭-穩-水平段”五段制井眼軌道優化設計方法，以入靶精度和最短井深作為雙優化目標，以造斜段造斜率和扭方位段全角變化率作為約束條件，建立了多目標約束的三維水平井軌道優化設計模型。

(2)通過對本文所建立的模型與文獻對比可知，本文所提出模型不僅滿足靶點位置不確定性要求，同時在造斜段和扭方位段的狗腿度更小，優化設計的軌道更加平緩。

(3)本文所提出的優化軌道設計模型具有良好的應用型，同時對于其他相同類型軌道優化設計工作具有借鑒意義。