含時(shí)變延遲且控制方向未知的自適應(yīng)迭代學(xué)習(xí)

夏元天,周菊香,徐天偉

(云南師范大學(xué) 民族教育信息化教育部重點(diǎn)實(shí)驗(yàn)室,昆明 650000)

0 概述

自動(dòng)化系統(tǒng)在建模和實(shí)際應(yīng)用過程中存在不確定性和不精確性的問題,使用傳統(tǒng)的PID控制、最優(yōu)控制等技術(shù)難以解決上述難題。迭代學(xué)習(xí)控制(Iterative Learning Control,ILC)[1-3]和重復(fù)控制(Repeat Control,RC)[4-5]很早被提出且得到了很好的發(fā)展。ILC作為一種克服傳統(tǒng)控制設(shè)計(jì)局限性的有效控制技術(shù)[6-7],其善于在有限的時(shí)間間隔內(nèi)處理重復(fù)的控制任務(wù)。文獻(xiàn)[1-3]提出一種新的ILC方法用來補(bǔ)償基于收縮映射的ILC。文獻(xiàn)[8]針對(duì)一類具有延遲性能的線性系統(tǒng)提出一種ILC協(xié)議。文獻(xiàn)[9]提出一種基于PID-type的ILC算法。總的來說,ILC以其良好的全時(shí)間間隔軌跡跟蹤性能已廣泛用于各類控制領(lǐng)域。

受控系統(tǒng)的時(shí)延效應(yīng)會(huì)降低系統(tǒng)性能,甚至?xí)?dǎo)致系統(tǒng)癱瘓。文獻(xiàn)[10]引入分離技術(shù),用以解決時(shí)延效應(yīng)帶來的影響。文獻(xiàn)[11]為了解決一類不確定非仿射非線性時(shí)變時(shí)滯系統(tǒng)的自適應(yīng)控制問題,提出一種新的拉祖米欽-努斯鮑姆引理。文獻(xiàn)[12]通過引入飽和函數(shù),構(gòu)造出一種新的ILC機(jī)制。文獻(xiàn)[13]針對(duì)不確定非線性時(shí)變時(shí)滯系統(tǒng)中存在的非仿射非線性故障問題,提出一種基于模糊逼近的自適應(yīng)容錯(cuò)跟蹤控制方法。文獻(xiàn)[14]利用神經(jīng)逼近技術(shù)和努斯鮑姆函數(shù)法設(shè)計(jì)一種自適應(yīng)ILC方案。文獻(xiàn)[15]提出一種自適應(yīng)迭代學(xué)習(xí)控制(AILC)方案,用以解決一類具有未知時(shí)變延遲和輸入飽和的非線性參數(shù)化系統(tǒng)。文獻(xiàn)[16]針對(duì)一類具有未知時(shí)變參數(shù)和時(shí)變時(shí)滯的非線性系統(tǒng),通過參數(shù)分離技術(shù)并結(jié)合信號(hào)替換機(jī)制,提出了一種新的AILC方法。

控制方向在系統(tǒng)的設(shè)計(jì)過程中起著關(guān)鍵性的作用。Nussbaum增益技術(shù)則是解決控制方向未知問題的一種常用方法[17-18]。文獻(xiàn)[19]提出一種跟蹤周期軌跡的連續(xù)通用重復(fù)學(xué)習(xí)控制方法。文獻(xiàn)[20]將Nussbaum增益技術(shù)引入至Backstepping方法中,以解決控制方向未知的船舶航向系統(tǒng)的穩(wěn)態(tài)性能控制問題。文獻(xiàn)[21]采用參數(shù)分離技術(shù)和信號(hào)置換思想來處理系統(tǒng)中出現(xiàn)的時(shí)滯項(xiàng),利用Nussbaum增益技術(shù)解決未知控制方向等問題。文獻(xiàn)[22]提出一種數(shù)據(jù)驅(qū)動(dòng)的約束范數(shù)最優(yōu)迭代學(xué)習(xí)控制框架,用以解決跟蹤問題和點(diǎn)對(duì)點(diǎn)運(yùn)動(dòng)問題。文獻(xiàn)[23]提出一種基于倒推和DSC相結(jié)合的自適應(yīng)徑向基函數(shù)神經(jīng)網(wǎng)絡(luò)控制方法。文獻(xiàn)[24]通過變換系統(tǒng)形式和采用Butterworth低通濾波器解決控制方向未知的問題。文獻(xiàn)[25]提出一種新的基于截?cái)嗟恼{(diào)節(jié)方法,使算法能夠自適應(yīng)地找到正確的控制方向。文獻(xiàn)[26]提出一種基于障礙Lyapunov函數(shù)的反步自適應(yīng)控制方法,首次解決了控制方向未知的全狀態(tài)約束非線性系統(tǒng)的跟蹤控制問題。文獻(xiàn)[27]在不使用努斯鮑姆增益的情況下,提出一種求解離散系統(tǒng)未知控制方向問題的新方法。文獻(xiàn)[28]提出一種魯棒自適應(yīng)迭代學(xué)習(xí)控制算法。

本文在上述研究的基礎(chǔ)上進(jìn)行改進(jìn),設(shè)計(jì)一種新的自適應(yīng)迭代學(xué)習(xí)策略。利用微分-差分耦合型參數(shù)自適應(yīng)律解決了雙線型參數(shù)中存在的時(shí)變和時(shí)不變類型的問題。使用局部的李普希茨連續(xù)條件,使得非參數(shù)化得到了良好的處理。將Nussbaum技術(shù)與ILC方法相結(jié)合,解決了系統(tǒng)中存在的控制方向未知問題。基于信號(hào)替換思想和參數(shù)重組技術(shù),將具有時(shí)延的所有項(xiàng)組合成新的時(shí)變參數(shù),使得時(shí)變延遲問題得到了解決。

1 問題描述

本文設(shè)計(jì)的自適應(yīng)迭代學(xué)習(xí)策略可表示為:

(1)

其中,t∈[0,T],T>0且為已知常數(shù),xi(t)∈R為系統(tǒng)狀態(tài),ui(t)∈R為控制輸入,?(t)∈R為隨時(shí)間變化的連續(xù)型參數(shù)且未知,θ∈R是與時(shí)間變化無關(guān)的連續(xù)型參數(shù)且未知,并假設(shè)其大于零。ξ(xi,t)為非線性連續(xù)函數(shù)且已知,f(,)是未知連續(xù)函數(shù),g(xi,t)為未知的非線性函數(shù),滿足局部Lipschitz連續(xù),τ(t)∈C[0,T]為未知時(shí)變延遲,且滿足τ(t)≤τmax,?t∈[0,T],τmax為已知常數(shù),i∈Z+為迭代次數(shù),v(t)給出了起始條件且為已知的連續(xù)型函數(shù),b(t)≠0為時(shí)變參數(shù)且未知,控制方向由其正負(fù)決定。

假設(shè)2f(,)滿足李普希茨連續(xù)條件,即:

|f(xi(t-τ(t)),t)-f(xd(t-τ(t)),t)|≤

l(|xi(t-τ(t))-xd(t-τ(t))|)

其中,l為未知的李普希茨常數(shù)。

假設(shè)3xi(0)=xi-1(T),xd(0)=xd(T)。

假設(shè)4系統(tǒng)1滿足xi(t)=xd(t),t∈[-τmax,0],顯然ei(t)=0,t∈[-τmax,0],?i∈Z+。

假設(shè)5g(x,t)是未知非線性函數(shù)且滿足李普希茨連續(xù)條件,即:

定義1v(·)為Nussbaum函數(shù),且滿足以下條件:

(2)

引理1v(·)和k(·)在[0,tf]上為光滑函數(shù),?t∈[0,tf],V(t)≥0,b(t)在B=[b-,b+],0?B內(nèi)取值。若式(3)成立:

(3)

2 自適應(yīng)迭代學(xué)習(xí)控制設(shè)計(jì)

下式為ei的k次迭代方程:

b(t)ui(t)+g(xi,t)+f(xd(t-τ(t)),t)-

f(xd(t-τ(t)),t)]=?(t)ξ(xi,t)θ+

b(t)ui(t)+g(xi,t)+φ(t)+Λi

(4)

由假設(shè)2可知,Λi滿足以下條件:

|Λi|≤l(|xi(t-τ(t))-xd(t-τ(t))|)≤

l(|ei(t-τ(t))|)

(5)

針對(duì)系統(tǒng)1設(shè)計(jì)一個(gè)處理時(shí)變時(shí)延遲的李雅普諾夫函數(shù),具體如下所示:

(6)

由式(6)給出Lyapunov函數(shù)的導(dǎo)數(shù)如下所示:

(7)

將式(4)代入式(7)可得:

(8)

由式(5)可得:

eiΛi≤|ei||Λi|≤l|ei||ei(t-τ(t))|

(9)

(10)

將式(10)代入式(8)可得:

ei[?(t)ξ(xi,t)θ+b(t)ui(t)+g(xi,t)-

ei[?(t)ξ(xi,t)θ+b(t)ui(t)+g(xd,t)+φ(t)+

(11)

由假設(shè)5得到:

(12)

將式(12)代入式(11)中,得到:

(13)

第i次迭代的控制律為:

(14)

?(t)的學(xué)習(xí)律為:

(15)

θ的學(xué)習(xí)律為:

(16)

L的學(xué)習(xí)律為:

(17)

(18)

(19)

(20)

3 收斂性分析

定理1系統(tǒng)(1)在假設(shè)1～假設(shè)5、學(xué)習(xí)控制律式(14)以及參數(shù)學(xué)習(xí)律式(15)～式(17)下,保證了:

2)閉環(huán)系統(tǒng)所有信號(hào)有界。

證明構(gòu)造的Lyapunov泛函為:

(21)

對(duì)任意t∈[0,T],V(t)在區(qū)間[0,T] 上的差分為:

ΔV(t)=(V1,i(t)-V1,i-1(t))+

(22)

根據(jù)式(4)和式(14)計(jì)算式(22)右邊第1項(xiàng)可得:

α(xi,xd,t)ei(t)]dσ+V1,i(0)-V1,i-1(t)=

V1,i(0)-V1,i-1(t)

(23)

(24)

根據(jù)參數(shù)學(xué)習(xí)律式(16),計(jì)算式(22)右邊第4項(xiàng)可得:

(25)

根據(jù)式(17),計(jì)算式(22)右邊第5項(xiàng)可得:

(26)

將式(23)～式(26)分別代入式(22)可得:

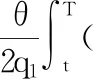
(27)

(28)

重復(fù)利用式(28)可以得到:

(29)

(30)

進(jìn)一步得到Vi(t)的倒數(shù)為:

(31)

表示E(t+(i-1)T)=Vi(t)。對(duì)?t∈[0,T],由式(29)～式(31)可得:

(32)

當(dāng)i→,可以得到:

(33)

下面證明V0(T)的有界性。

對(duì)任意?t∈[0,T],V0(t)的倒數(shù)為:

(34)

對(duì)式(34)兩端從0到T進(jìn)行積分可得:

(35)

(36)

?(t)在[0,T]上是連續(xù)型函數(shù),因此?(t)在[0,T]上為有界函數(shù),綜合已知條件得,存在M1,M2,M3,M4使下式成立:

(37)

將式(37)代入式(36)可得:

V0(0)=M1+M2+M3+M4<

(38)

證明結(jié)束。

4 實(shí)例仿真

不確定系統(tǒng):

目標(biāo)軌線:

xd(t)=cost

在仿真實(shí)驗(yàn)中取:t∈[0,2π],η=0.5,c=0.5,q1=0.5,q2=0.4,q3=0.5

1)當(dāng)b(t)>0時(shí),取b(t)=5+0.2sin(πt)。通過仿真實(shí)驗(yàn)得出系統(tǒng)中各參數(shù)的迭代曲線圖如圖1～圖6所示。

圖1 最大跟蹤誤差|ei|sup變化曲線1

圖2 Nussbaum型函數(shù)v(·)變化曲線1

圖3 時(shí)變參數(shù)?(t)的變化曲線1

圖4 時(shí)不變參數(shù)θ的變化曲線1

圖5 時(shí)不變參數(shù)L的變化曲線1

圖6 控制器ui(t)的變化曲線1

2)當(dāng)b(t)<0時(shí),取b(t)=-(5+0.2sin(πt))。通過實(shí)驗(yàn)仿真,得出系統(tǒng)中各參數(shù)的迭代曲線圖如圖7～圖12所示。

圖7 最大跟蹤誤差|ei|sup的變化曲線2

圖8 Nussbaum型函數(shù)v(·)的變化曲線2

圖9 時(shí)變參數(shù)?(t)的變化曲線2

圖10 時(shí)不變參數(shù)θ的變化曲線2

圖11 時(shí)不變參數(shù)L的變化曲線2

圖12 控制器ui(t)的變化曲線2

從圖1～圖12可以看出,本文設(shè)計(jì)的非線性系統(tǒng)在迭代次數(shù)小于20次的情況下,系統(tǒng)的最大跟蹤誤差和Nussbaum型函數(shù)已經(jīng)開始收斂于0。根據(jù)文獻(xiàn)[29]設(shè)計(jì)的非線性系統(tǒng)以及提供的仿真結(jié)果表明,在方向?yàn)榉菚r(shí)變常參數(shù)且不包含時(shí)變延遲的情況下,其系統(tǒng)最大跟蹤誤差以及Nussbaum型函數(shù)在迭代次數(shù)120次以上才開始趨于收斂于0。通過與文獻(xiàn)[29]比較可得出,在時(shí)變未知控制方向和含有時(shí)變延遲的雙重不確定條件下,本文設(shè)計(jì)的系統(tǒng)依然能夠以較少的迭代次數(shù)以及較高的執(zhí)行效率運(yùn)行,也說明了本文系統(tǒng)在時(shí)效上的優(yōu)越性和可行性。

5 結(jié)束語

本文針對(duì)控制方向未知且含有非線性延遲及參數(shù)和非參數(shù)化的不確定性系統(tǒng)進(jìn)行了深入分析。利用Nussbaum函數(shù)和通過導(dǎo)入差分耦合型更新定律,并結(jié)合Lyapunov函數(shù)給出系統(tǒng)收斂的充分條件,設(shè)計(jì)出全新的自適應(yīng)迭代方案,使跟蹤誤差最終收斂于0,并證明各信號(hào)的有界性。仿真結(jié)果證明了本文設(shè)計(jì)的合理性以及結(jié)果的可行性。

通過以上理論推導(dǎo)和實(shí)驗(yàn)仿真結(jié)果說明本文設(shè)計(jì)的自適應(yīng)迭代學(xué)習(xí)策略在一階系統(tǒng)中的有效性。在下一步研究工作中,可以考慮將其應(yīng)用到二階或高階的非線性不確定系統(tǒng)中,通過與其他相關(guān)技術(shù)相結(jié)合,用以解決未知控制方向和時(shí)變延遲對(duì)高階不確定系統(tǒng)產(chǎn)生的影響。