參數自動優化的特征選擇融合算法①

吳 俊,柯飂挺,任 佳

(浙江理工大學 機械與自動控制學院,杭州 310018)

隨著現代科技的飛速發展,大量數據從各個領域中呈爆炸式不斷產出.同時因為這些數據中含有大量不相關、冗余信息,在進行數據挖掘時,預處理技術中的特征選擇便變得極為重要和極具挑戰性[1].

目前特征選擇已經在文本分類[2]、模式識別[3-5]、癌癥分類[6]和故障診斷[7]等領域內成功應用.特征選擇可定義為從數據集中去除不相關和冗余的特征,從而增強后續學習算法性能的過程[8].特征選擇方法可根據兩個標準來分類:搜索策略和評估標準[8].特征子集可以通過兩種模型獲取:過濾式[9]模型和封裝式[10]模型.過濾式模型在搜索過程中僅考慮數據集本身,而封裝式模型需在搜索過程中結合學習算法.因此過濾式模型花費時間成本較小,但準確率不穩定.反觀封裝式模型,由于需要結合學習算法,所以準確率相對更高,同時也更耗時.此外搜索最優子集的方式也是特征選擇中的一個關鍵問題,具體可分為遍歷、隨機搜索和啟發式搜索.其中遍歷雖然一定可以獲取最優子集但是不適用于大型數據集[11].隨機搜索則因為沒有數學理論引導搜索方向導致搜索性能不穩定[12].而啟發式算法使用啟發式信息指導搜索.雖然不能保證找到最優解,但可以再合理的時間內獲取可接受的解[13].近年已經有許多研究對不同特征選擇算法進行了對比,如在文獻[14]中,使用了3種不同的分類器評估了8種標準的特征選擇方法.文獻[10]使用了K 最近鄰算法作為分類器,系統地研究了鯨魚優化算法(Whale Optimization Algorithm,WOA)并將基于WOA的封裝式特征選擇算法和三種標準的啟發式特征選擇算法進行比較證明了WOA的強大性能.文獻[15]中將融合啟發式算法和3種標準的封裝式特征選擇算法進行了對比以證明融合啟發式算法的潛力.

綜上,本文基于過濾式模型和封裝式模型各自的特點,將這兩種模型結合,構建一種基于最大互信息系數和皮爾遜相關系數的、使用遺傳算法進行超參數自動優化的兩階段特征選擇融合算法(A feature selection fusion method based on Maximal Information Coefficient and Pearson correlation coefficient with parameters automatic optimized by Genetic Algorithms,MICP-GA),通過結合使用最大互信息系數、皮爾遜相關系數的過濾式模型和以分類準確率為目標的封裝式模型來克服過濾式模型準確率較低,傳統相關系數處理非線性關系能力較弱以及封裝式模型的時間成本過高的問題.第一階段根據最大互信息系數獲取各特征和標簽之間的相關度評分,該評分綜合考慮線性和非線性相關度,再設置相關度閾值以剔除不相關特征.第二階段,通過皮爾遜相關系數獲取特征子集特征之間的線性冗余度評分,同樣設置冗余度閾值來刪除冗余特征.最后,將特征子集的分類準確率作為評價標準,使用遺傳算法自動優化前兩步中的超參數,達到綜合減少特征數目和維持甚至提高特征子集分類精度的效果,并自動獲取最優特征子集.

1 基礎理論

1.1 信息熵與最大互信息系數

定義1.信息熵[16]克服了對信息隨機變量不確定性的度量,設X為離散隨機變量,那么X的信息熵H(X)為:

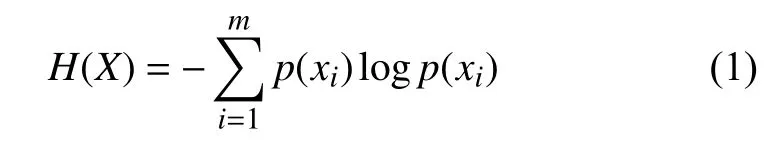
定義2.條件熵表示為當隨機變量Y單獨發生時,隨機變量X發生的條件概率分布,可通過式(2)表示:

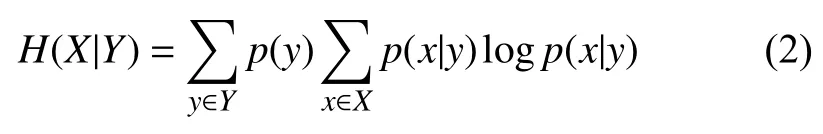
定義3.互信息用于檢測兩隨機變量中所含的信息量和互相關聯程度.互信息可通過式(1)和式(2)用熵表示:

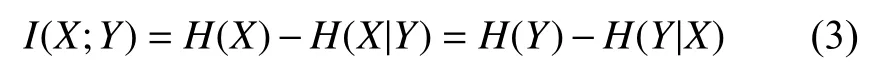
最后依據式(2)和式(3)可得:

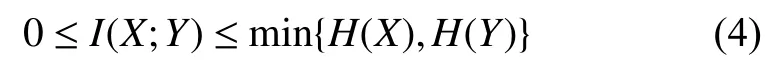
Reshef 等人[17]提出的最大互信息系數(Maximal Information Coefficient,MIC)無需對數據分布進行任何假設便可評估變量間的函數關系和統計關系.該算法具有普適性和均勻性兩大特點,普適性指當數據規模足夠大時,MIC算法能有效捕捉到大規模有意義的關系,而并不會僅局限于某種函數關系;均勻性則指對于不同類型函數關系,當給予相同噪聲時,MIC算法給出相同或相近的結果變化.最大互信息系數Imax(X;Y)可通過互信息和熵計算得出:

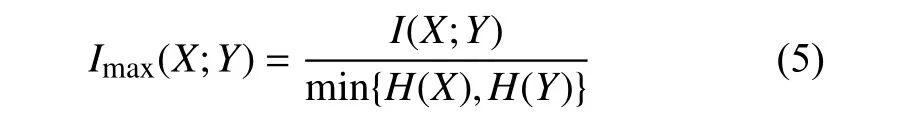
1.2 皮爾遜相關系數

皮爾遜相關系數(Pearson Correlation Coefficient,PCCs)由Karl Person 提出,因其計算簡單、運算速度快而被廣泛用于度量在數據預測、故障診斷和參數估計等領域中兩變量間的線性相關程度,其取值范圍是[?1,1].兩變量間相關系數的絕對值越大,表明兩者的相關度越高,當取值為0時表示兩個變量不相關.具體相關系數數值大小和相關判斷結果的對應關系見表1.

通常皮爾遜相關系數用希臘字母ρ表示.其具體定義為兩個變量之間的協方差和標準差的商,其中cov表示協方差,E為數學期望:

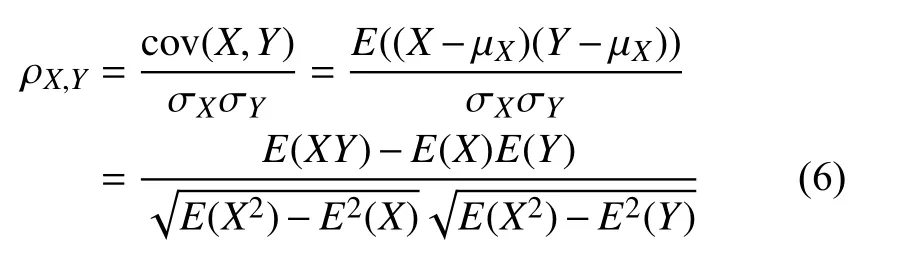
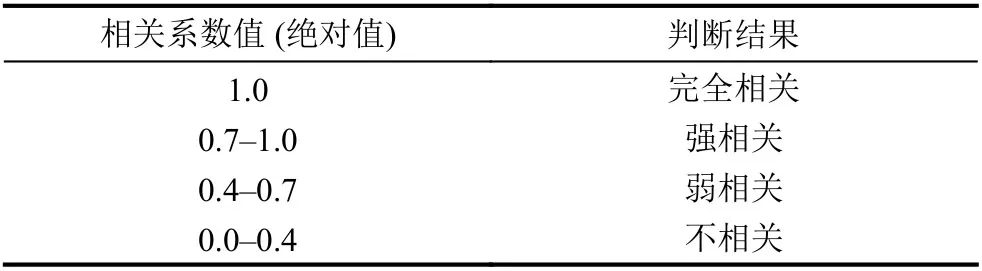
表1 相關性判斷準則

1.3 遺傳算法

遺傳算法的靈感來自生物的遺傳過程,該算法的解被稱為染色體或個體.二進制遺傳算法的每個染色體包含二進制值為0或1的基因,這些基因決定了每個個體的屬性.一系列的染色體組成了一個種群.每個染色體的性能通過適應度函數來評估,適應度值較高的染色體被選作父代,并通過交叉步驟結合產生新的后代.再對新的種群進行變異處理來增加個體的隨機性,降低陷入局部最優的可能[18].

2 MICP-GA 基礎理論

MICP-GA算法兼顧過濾式和封裝式特征選擇算法的優點,同時利用遺傳算法對前述步驟中的超參數進行自動優化來獲取最優特征子集.該算法的實現流程如圖1所示.

2.1 運用最大互信息系數獲取各特征和標簽的相關度

本階段利用最大互信息系數進行初次特征選擇.第一階段特征選擇的具體步驟如算法1所示.

該方法使用最大互信息系數準確找出和類別線性相關、非線性相關的特征,剔除不相關的特征,但篩選出的特征之間仍可能存在線性冗余.為解決該問題,繼續進行第二步特征選擇.

2.2 基于皮爾遜相關系數的特征去冗余

對第一步選取的特征子集D2,使用皮爾遜相關系數,減少特征之間的冗余性,同時也減少了D2的特征數量,幫助后續學習算法更快地獲取結果.第二階段特征選擇的步驟如算法2所示.

由前述可知,第一階段中的超參數a和第二階段中的閾值b這兩個參數值對分類結果有著重要的影響.接下來,以UCI標準數據集中的Vehicle數據集為例進行說明:該數據集初始特征共計18 維,如在第一階段特征選擇時設定a為18,則保留全部特征.現對所選的Vehicle、Ionosphere、Wine和Sonar數據集中的特征的皮爾遜相關系數進行可視化處理,如圖2～圖5所示.熱力圖中,兩兩特征之間的皮爾遜相關系數的取值范圍是[0,1],對應著圖中不同的顏色.此外,由于熱力圖沿著正對角線(如圖2～圖5中從左上貫穿至右下的藍線所示)對稱,所以僅觀察熱力圖的左下部分即可.由圖可知,其中若干區域(如圖2～圖5中藍色圈注所示)中特征之間的皮爾遜相關系數較大,說明該區域內的特征之間存在線性冗余.可采用基于皮爾遜相關系數的特征選擇算法有效解決該問題.

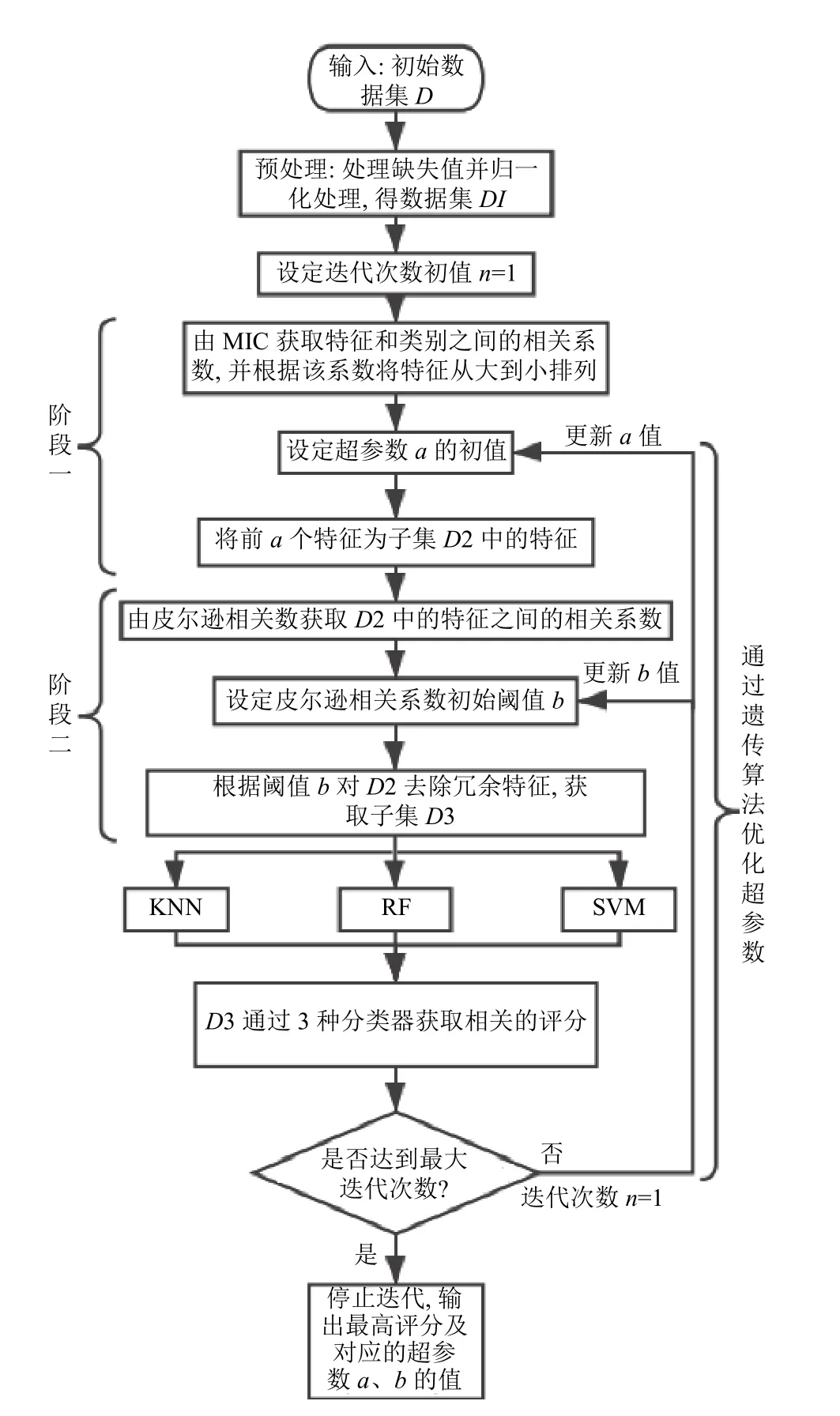
圖1 整體算法流程圖

算法1.基于最大互信息系數的特征選擇算法輸入:數據集D1.步驟1.設定超參數a.Imax(x(i);y)步驟2.根據式(5)計算每個特征x(i)與類別y 的最大互信息系數.{x(1),x(2),···,x(N)}步驟3.將特征按照最大互信息系數的大小,從大到小排列,獲取排序后的特征集.D2={x(1),x(2),···,x(a)}步驟4.從排序后的特征集中選擇前a 個特征,構成特征子集.輸出:特征子集D2.

算法2.基于皮爾遜相關系數的特征選擇算法輸入:特征子集D2.步驟1.設定皮爾遜相關系數冗余閾值b.步驟2.根據式(6)計算D2 中所有特征之間的皮爾遜相關系數.步驟3.將皮爾遜相關系數大于閾值b 的兩個特征中最大互信息值較小的特征刪除.步驟4.反復執行步驟3 直至特征子集中所有特征的皮爾遜相關系數值都大于b,該特征子集記作D3.輸出:最終特征子集D3.

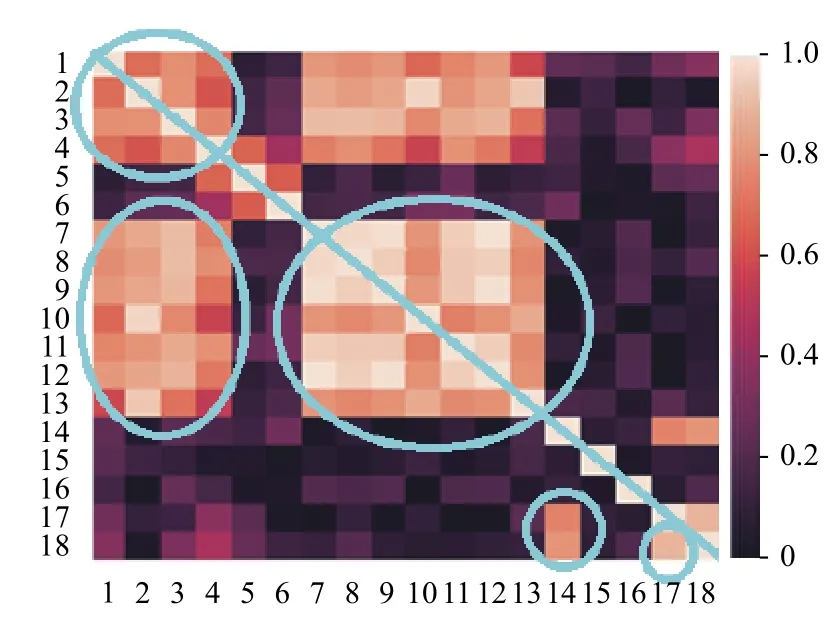
圖2 Vehicle數據的皮爾遜相關系數熱點圖

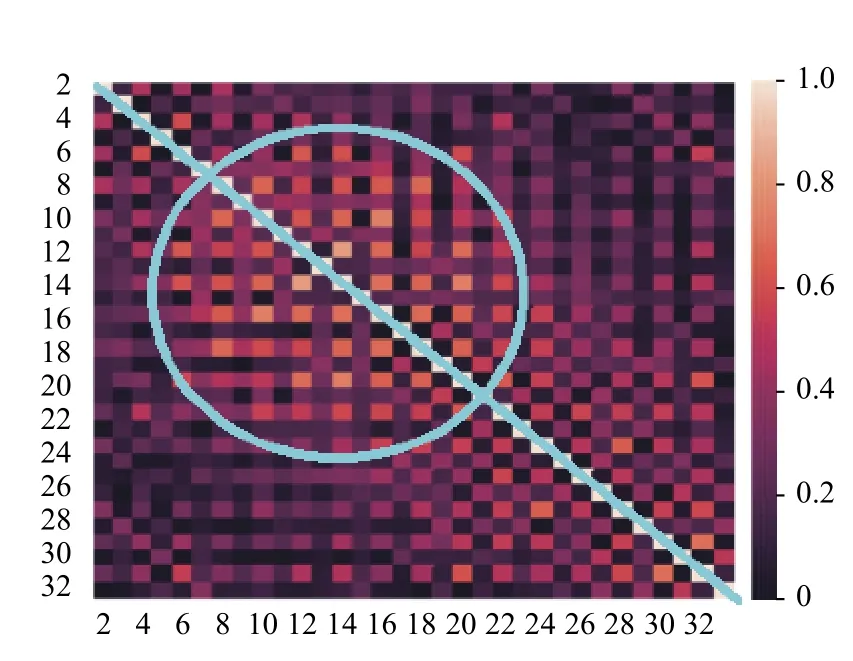
圖3 Ionosphere數據的皮爾遜相關系數熱點圖

圖4 Sonar數據的皮爾遜相關系數熱點圖

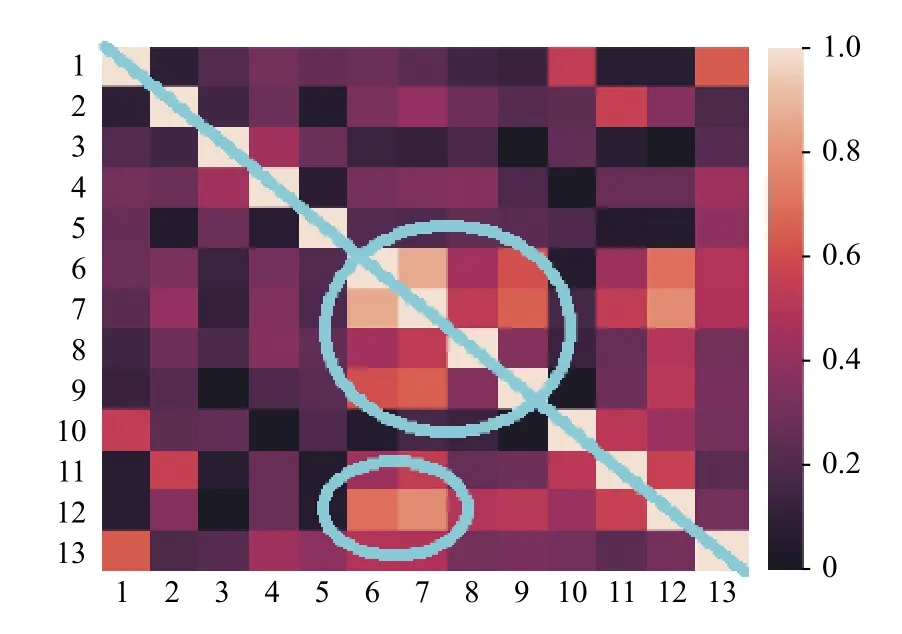
圖5 Wine數據的皮爾遜相關系數熱點圖

2.3 使用遺傳算法實現超參數的自動優化

本文采用遺傳算法自動優化3.1和3.2節中的超參數a和b.遺傳算法優化超參數的步驟描述如算法3所示.

此外染色體個數NIND設為5.最大迭代次數MAXGEN設為20.子代和父代個體不相同的概率GGAP設為0.9.遺傳算法選擇方式SELECTSTYLE選用輪盤賭選擇法rws.基因變異的概率PM由源代碼中的0.1 修改為由式(7)獲取,令PM隨著迭代次數t的增加而不斷減小,使得算法在搜索前期擴大搜索空間,不容易陷入局部最優解,而且在搜索后期也不會因為PM過大導致子集狀態有較大突變.

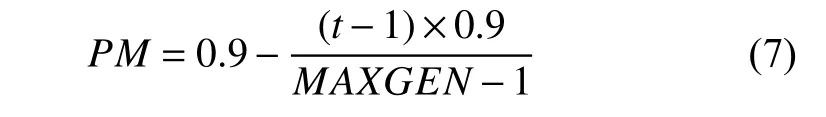
綜上所述,本文提出的遺傳算法可對前兩步驟中的待優化超參數a、b自動進行優化,并以適應度函數Fitness作為目標函數,將Fitness取得最小值時對應的a、b作為最優參數.

算法3.使用遺傳算法實現超參數的自動優化步驟1.初始化染色體個數NIND和各個染色體中的超參數a和b.fitness=AR+BMN步驟2.根據超參數a、b 結合階段一、二的步驟獲取各個染色體對應的特征子集,通過適應度函數計算各個染色體的適應度值fitness,并記錄本輪獲取的最小適應度值fitness*和對應的參數a*、b*(其中R表示給定分類器的平均錯誤率,M表示所選子集中特征的個數,N表示初始數據集中所有特征的個數,其中A和B分別是來自文獻[18]與分類準確率和子集長度對應的兩個參數,A∈[1,0],B∈[0,1-A]).步驟3.設定迭代次數t的初值和最大迭代次數MAXGEN.t=t+1 fitnessbest= fitness?步驟4.使用遺傳算法更新超參數a和b,迭代次數,重復步驟2,若本輪最優適應度值fitness*小于歷史最優適應度值.fitnessbest,則,并覆蓋對應的超參數a*和b*,其中超參數a∈[2,N],b∈[Min(PCCs),Max(PCCs)],Min(PCCs)和Max(PCCs)分別表示各個子集的特征之間的皮爾遜相關系數的最小值和最大值.其中a的閾值設置為[2,N]是為了確保搜索算法的搜索空間完整,最小值取2 而不是取1 則是考慮到代碼參數個數需求.步驟5.若迭代次數t 等于最大迭代次數MAXGEN,終止迭代并輸出歷史最優適應度值fitnessbest和對應超參數a、b.

3 實驗分析

為檢測上文提出的MICP-GA算法的可靠性,本文選取了5個UCI標準數據集.表2和表3分別列出了這些測試數據集的具體信息以及直接將各數據集初始數據用于不同分類器時的分類準確率.

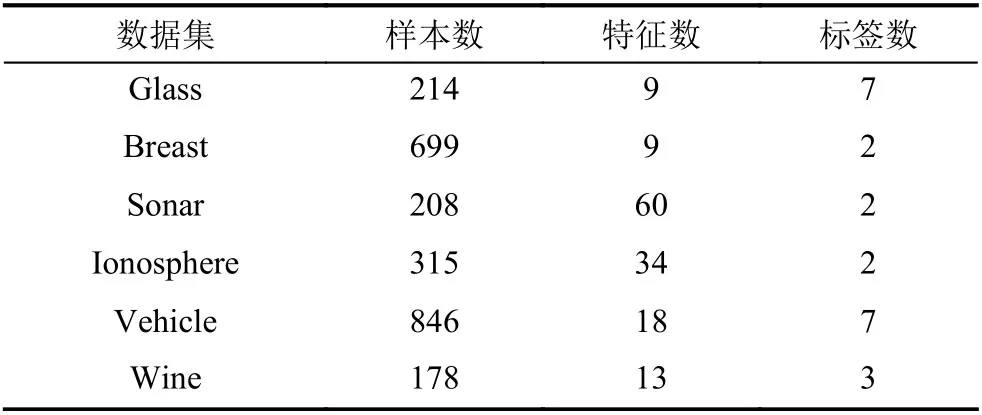
表2 測試數據集

在測試中,使用Python3進行編程,并且使用常規的十折交叉驗證用于檢驗.接下來使用3種特征選擇方法對上述數據集進行測試和比較,3種方法分別是MICP-GA、單獨用MIC特征選擇以及單獨使用皮爾遜相關系數特征選擇.在測試過程中,將3種特征選擇方法與三種典型分類器,K 最近鄰分類器(K-Nearest Neighbors,KNN)、隨機森林分類器(Random Forest,RF)和支持向量機(Support Vector Machine,SVM)結合后,對上述數據集進行測試.結果顯示平均最高準確率如表4所示,平均特征選取率如表5所示,平均適應度函數如表6所示.對比表3和表4的分類準確率,可見本文提出的算法對原始數據的分類準確率有明顯提升,說明MICP-GA在搜索最優特征選擇的組合時能夠有效跳出局部最優,確保搜索到的解是近似全局最優解,同時說明MICP-GA 充分考慮特征和類別之間的包括線性和非線性的關系,解決了傳統相關系數處理非線性關系表現不好的問題,并根據MIC 評分來判斷刪除每對冗余特征中的哪一個,較好地結合了運用MIC和PCCs的特征選擇從而使得分類效果比單獨使用MIC或PCCs時更優.同時,結合表5中基于不同特征選擇方法的分類器的平均特征選取率,也表明了該算法在降低數據維度方面有較優的表現,能夠有效剔除和類別不相關的特征以及冗余特征,為后續學習算法節省大量的運算成本,提升了運行效率.綜上所述,本文提出的算法充分考慮了特征和類別之間的線性相關性以及特征之間的冗余性,能夠有效對數據進行降維同時保證數據集的分類準確率保持不變甚至提升分類準確率.

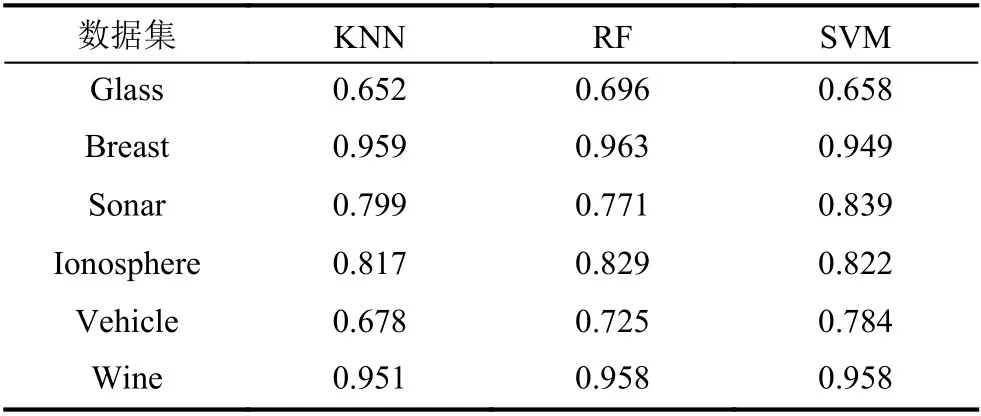
表3 基于不同分類器的初始數據集的平均分類準確率

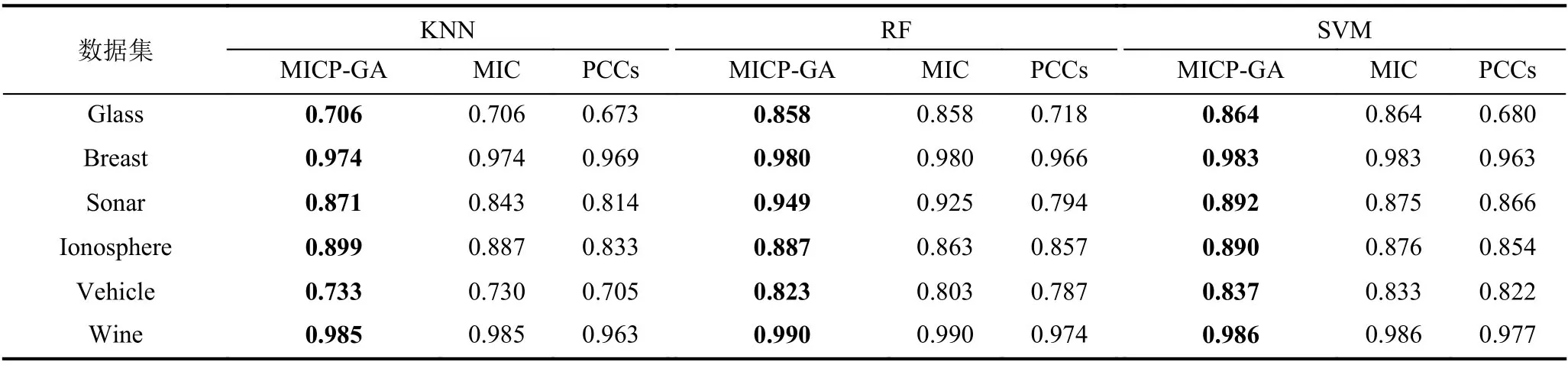
表4 基于不同特征選擇方法的分類器的平均最高準確率

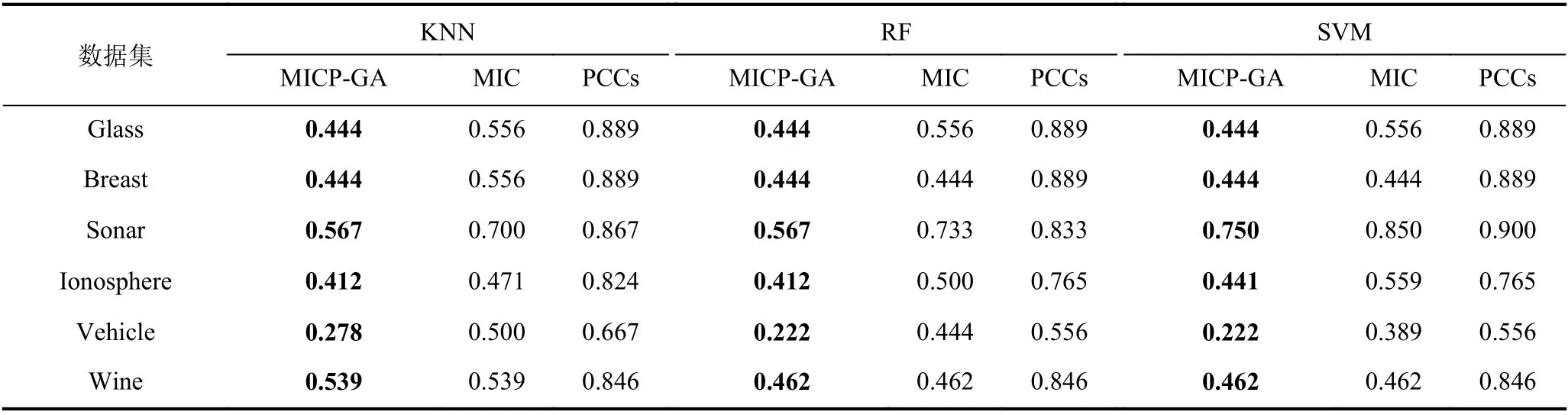
表5 基于不同特征選擇方法的分類器的平均特征選取率

表6 基于不同特征選擇方法的分類器的平均適應度值

4 結論與展望

特征選擇算法的優劣對模型的預測準確率有著重要影響,Filter可以快速高效地去除冗余特征及不相關特征,但是無法保證獲取的特征子集準確率達標.Wrapper 更傾向于獲取準確率更高的特征子集,所以其時間成本一般遠高于前者.本文針對以上兩種方法的特點,將其進行結合提出了MICP-GA方法,所提算法兼顧了兩者的優點并且在UCI標準數據集中也有較好的表現.但是因為結合了遺傳算法以及最大互信息系數,導致時間復雜度比傳統特征選擇方法更高,根據文獻[10]可見傳統的全局搜索算法在性能和運算復雜度上并沒有較大差別,所以沒有將GA 替換成其他全局搜索算法.而如果使用單解的搜索算法如模擬退火(Simulated Annealing,SA)算法替換GA 確實可以較快獲取解,但鑒于SA 極其容易陷入局部最優,因此不考慮用SA 搜索最優特征子集.所以如何加快搜索速度是后續進一步的研究課題.