衛星導航模擬器低軌用戶軌跡仿真方法
李 笛,孫騰達
(衛星導航系統與裝備技術國家重點實驗室,河北 石家莊 050081)
0 引言
衛星導航模擬器[1]可以通過數據仿真產生在接收機各種運動狀態下的導航信號,可以直觀地呈現衛星導航系統衛星的空間分布與可見性信息,用戶的位置、速度等軌跡信息和接收機接收觀測量信息等。因此,衛星導航模擬器廣泛用于各種應用場景中接收機的調試與測試[2]。低軌衛星廣泛用于探測、通信和導航增強等[3],發揮著越來越重要的作用,在低軌衛星任務的地面仿真中,衛星導航模擬器發揮著不可替代的作用。其中,低軌用戶軌跡長時間、高精度仿真是模擬器正確仿真觀測量的基礎,其仿真精度直接影響低軌用戶數據仿真的逼真度。由于低軌衛星受力情況非常復雜,實現其高精度軌跡仿真特別困難,同時在模擬器中運行還需考慮工程可實現性,針對上述問題,開展低軌用戶高精度軌跡仿真方法研究,并兼顧精度與計算量,提升工程的可實現性。
1 低軌用戶動力學模型
低軌用戶軌跡分布取決于空間復雜的力學環境[4],故建立相對精確的動力學模型[5]對低軌用戶軌跡仿真至關重要。低軌用戶在軌運行期間,除了受地球中心引力[6]作用外,還將受到地球非球形引力[7],太陽、月球及其他天體引力的影響,以及太陽光壓、大氣阻力和地球潮汐力等因素的影響。
1.1 重力場模型
在初步分析航天器運動規律時,把地球看作理想球體,其對航天器產生指向地心的、大小與航天器質量m成正比而與地心與航天器距離r的平方成反比的引力F[8]:
(1)
由此得到地球引力常數:
μ=GM=3.986 000 441 5×1014m3/s2。
(2)
于是引力加速度為g=μ/r2,此情況下地球引力場稱為中心引力場。引力加速度為引力勢Uc的梯度,即Uc=μ/r。
地球并不是完美球體,具有扁平度、梨形和赤道變形等,因此,引力加速度是地心經度φ、緯度λ和r的函數。則地球引力加速度矢量g為地球引力勢函數U的梯度:
g=gradU(r,φ,λ)。
(3)
目前引力勢函數的普遍表達[8]為:
([Cn,mcos(mλ)+Sn,msin(mλ)]},
(4)
式中,RE=6 378.136 3 km為地球赤道半徑;Pn,m(x)為n階m級的Legendre函數。為克服各階數系數相差太大而引起的計算誤差,采用的范化式[6]為:
(5)
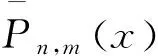
(6)
式中,
(7)
地球引力勢模型系數Jn(即-Cn,0),Cn,m,Sn,m由測量得到。許多國際組織通過不同手段測量重力場系數并創建對應的重力場模型,比較著名的重力場模型包括WGS系列、GEM系列和GRIM系列模型。WGS和GEM模型已經合并為EGM96模型,IER2003推薦采用EGM96模型。
1.2 大氣阻力模型
大氣對低軌用戶的作用包括三部分[6],與用戶對大氣流相對速度方向相反的大氣阻力、升力和副法線作用力,其中大氣阻力占支配地位,其余2種可以忽略。對低軌用戶而言,大氣阻力為其受到的最大的非引力性攝動力。
低軌用戶的大氣阻力加速度[6]為:
(8)
式中,r為低軌用戶位置矢量;CD為大氣阻力系數;A為低軌用戶迎風面;ρ為低軌用戶處的大氣密度;vr為用戶對大氣流的相對速度的大小;ev為相對速度的單位方向向量。
在大氣密度[9]計算方面,可采用目前最常用的3種經驗大氣密度模型,即Jacchia系列模型、DTM系列模型和MSIS系列模型。由于大氣變化機制復雜,任何經驗大氣密度模型都很難精確地刻畫大氣密度的實際變化。因此,為進一步提高大氣模型精度,可利用實際數據對經驗模型進行進一步校準。同時,由于不同軌道高度大氣密度不同,所以針對不同軌道類型的低軌衛星,還需研究不同經驗大氣密度模型下的軌道預報精度,探索選取最優的大氣密度計算方法。
在大氣阻力系數[10]計算方面,一般而言,在低軌衛星精密定軌中,常常將大氣阻力系數作為未知量與衛星的運動狀態矢量一起解算,解算得到的大氣阻力系數會吸收模型誤差,在軌道預報中利用解算得到的大氣阻力系數來計算大氣阻力加速度,但大氣阻力系數的較難準確地確定是制約解算大氣阻力加速度精度的一大原因。基于目前已有研究,可采用線性回歸分析建立大氣阻力系數的補償算法,還可基于空間環境數據和神經網絡模型對空間目標大氣阻力系數進行修正。同樣,針對不同軌道類型的低軌衛星還需研究不同大氣阻力系數算法下的軌道預報精度,探索選取最優的大氣阻力系數計算方法。
在低軌衛星迎風面積[11]計算方面,需對低軌衛星的幾何形狀進行描述,可采用Cannon-Ball模型和Macro模型。Canno-Ball模型是假設低軌衛星為一個球體,具有固定的形狀及單一的表面性質,對幾何形狀較為簡單的低軌衛星十分適用。Macro模型也被稱為Box-Wing模型,它會對低軌衛星每個面的幾何形狀都進行描述,包括面積、單位外法向量以及該面的光學特性(對可見光和紅外光的反射和吸收),特別當低軌衛星在飛行過程中太陽帆板發生翻轉時,Macro模型亦能做出幾何形狀的描述并反映到阻力計算中。
1.3 太陽光壓模型
照射到衛星上的太陽光對衛星產生入射作用力,衛星吸收一部分太陽光轉變成熱能和電能,另一部分被反射回去[12]。入射力和反射力統稱為太陽輻射壓力,也稱太陽光壓力。太陽輻射壓力產生的加速度與太陽光強度、垂直于入射方向的有效面積、表面反射率、與到太陽的距離和光速有關。由于衛星表面材料的老化、太陽能量隨太陽活動的變化以及衛星姿態控制的誤差等因素的影響,使得太陽輻射壓攝動也是難以精確模型的攝動力。
直接的太陽光壓力[6]可以表示為:
(9)
式中,P⊙為太陽常數,等于4.560 4×10-6N/m2,其物理意義是完全吸收的物體在距太陽一個天文單位(AU)處,單位面積上所受的輻射壓力;CR為太陽光壓系數;A為垂直于衛星與太陽方向的截面積;ν為蝕因子(地影區ν=0,衛星光照區ν=1,陰影區0<ν<1);r⊙為太陽的位置矢量。
1.4 N體攝動模型
太陽、月球和行星的引力攝動可近似用點質量來描述,在地心慣性系中,天體對衛星的N體引力加速度為:
(10)
式中,GMi為質點的引力常數;ri為質點在地心慣性系中的位置矢量。
2 坐標系及其轉換
為了減少牽連運動所引起的附加速度,使衛星的運動方程相對簡化,一般在慣性坐標系[5]中建立和求解衛星的運動方程。而地球對衛星的引力是在地固坐標系[13]中定義的。此外,衛星攝動力分析計算要涉及到衛星軌道坐標系,把加速度轉換到慣性坐標系或地固坐標系要涉及衛星固定坐標系。因此要建立衛星運動方程和參數估計的觀測方程,必須給出這些坐標系統的定義及其相互轉換關系。
2.1 坐標系統定義
2.1.1 協議慣性坐標系
具有絕對意義的慣性坐標系統是無法獲得的,人類只能根據科學任務的需要和一些約定建立相應精度的慣性坐標系統。通常使用的慣性坐標系統是協議慣性系[14](CIS),其具體實現就是國際協議天球參考框架(ICRF)。在CIS下,物體的運動可以以很高的精度滿足Newton力學定理,這對于動力學低軌軌跡仿真的相關研究十分重要。
2.1.2 協議地球坐標系
協議地球坐標系地固坐標系統[14](CTS)是為了描述地面觀測站位置所建立的與地球體聯結的坐標系統,依表達方式又可分為直角坐標系及大地坐標系。CTS是使用起來最直觀的坐標系統,它以特定的協議與地球固聯,并由一組全球參考站維持。
2.1.3 衛星軌道坐標系
為了便于對特定攝動力進行分析,將作用于低軌用戶的力分解到衛星軌道坐標系統[5](RTN)下進行分析。此外,在RTN系統下,還便于對各項誤差進行分析,如利用HL-SST模式研究恢復地球重力場時,徑向的軌道誤差占非常重要地位。
2.1.4 衛星固定坐標系
衛星固定坐標系[4](SBF)的主要作用是定義衛星在慣性空間中的姿態,同時建立各相關傳感器坐標系與慣性系的關系。如加速度計是固聯在衛星質心處,其軸系相應地平行于衛星固聯坐標系,在轉換加速度計觀測量到CIS或CTS時都需要使用SBF 作為中間過渡坐標系統。
2.2 坐標系統轉換方法
2.2.1 協議地球坐標系到協議慣性坐標系的轉換
如果以RCIS表示某點在歷元J2000.0對應的CIS中的坐標,以RCTS表示CTS中的坐標,則有[8]:
RCIS=P(t)N(t)S(t)Pm(t)RCTS,
(11)
式中,P(t),N(t),S(t),Pm(t)分別為歲差矩陣、章動矩陣、周日自轉矩陣和極移矩陣。極移矩陣將歷元平地球坐標系,即CTS轉換到瞬時極地球坐標系。地球自轉矩陣將瞬時極地球坐標系轉換到真天球坐標系。章動矩陣將真平天球坐標系轉換到瞬平天球坐標系。歲差矩陣將瞬平天球坐標系轉換到CIS[J2000.0]。根據IERS規范(McCarthy,1996),有[8]:
(12)
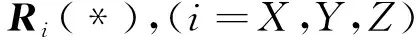
(13)
(14)
(15)
2.2.2 協議慣性坐標系到衛星軌道坐標系的轉換
RTN的3個坐標軸在CIS下的單位向量[14]為:
(16)
即:
RCIS=MRRTN
(17)
式中,RRTN為質點RTN坐標系中的三維位置;M為從RTN到CIS的轉換矩陣:
M=
(18)
2.2.3 衛星固定坐標系到協議慣性坐標系的轉換
從SBF到CIS的轉換可以通過太陽和衛星在協議慣性坐標系中的位置矢量來實現。更高精度轉換一般需要用到衛星的姿態數據。姿態數據給出的是由星體固定坐標系到協議慣性系轉換的四元數(或稱歐拉參數)q1,q2,q3,q4。由四元數表示的坐標轉換矩陣[14]為:
Q=
(19)
所以,將SBF下的向量RSBF轉換到CIS下的向量RCIS的公式為:
RCIS=QRSBF。
(20)
3 算法流程設計
在利用低軌衛星力學模型和坐標系統轉換建立低軌衛星軌跡信息(位置+速度)狀態方程的基礎上,兼顧軌跡準確度與工程計算量的要求,利用Runge-Kutta算法完成數值積分,得到各歷元時刻的低軌衛星軌跡信息。
3.1 Runge-Kutta數值積分算法
Runge-Kutta算法[6]是一種工程上廣泛應用的高精度單步算法。已知方程導數與初值信息:
(21)
式中,y0為矢量y的初值;f(t,y)為矢量y關于變量t的一階偏導數。則根據Runge-Kutta算法:
y(tn+1)≈y(tn)+h·Φ=η(tn+1) ,
(22)
式中,η(tn+1)為y(tn+1)的近似解;Φ為增量函數,h=tn+1-tn。根據經典RK4 Runge-Kutta算法[6],增量方程為:
(23)
式中,
(24)
根據Oliver Montenbruck和Eberhard Gill的研究,RK4解的局部截斷誤差[6]有以下特征:
eRK4=|y(tn+1)-η(tn+1))≤const·h5,
(25)
且RK4解與四階泰勒展開多項式精度相當:
(26)
式中,y(tn)(i),(i=2,3,4)為矢量y關于變量t的i階偏導數。
3.2 低軌用戶軌跡仿真算法設計
低軌用戶軌跡狀態量為其位置與速度[15],即

(27)
式中,R為低軌用戶三維位置矢量;V為其三維速度矢量。對于任意已知R,V,可低軌衛星受力模型與坐標轉化方法得到其對應的加速度α,則軌跡狀態量關于時間t的一階偏導數為:
(28)
在此基礎上,在給定初值R0,V0的前提下,利用RK4 Runge-Kutta算法即可計算得到各個歷元時刻的軌跡信息。
低軌軌跡仿真算法流程如圖1所示。

圖1 低軌軌跡仿真算法流程Fig.1 Flow chart of LEO track simulation algorithm
4 算法仿真及驗證
為了測試低軌用戶軌跡仿真算法的逼真性與可靠性[16-17],以STK10.0軟件仿真的低軌衛星軌道數據作為理論參考值進行測試驗證。
4.1 軌跡參數設定
軌跡仿真開始于UTC時間2010年1月1日0時0分0秒,持續86 400 s,仿真步長為10 s,輸出地心地固坐標系的位置速度。低軌用戶的六參數設置如表1所示。
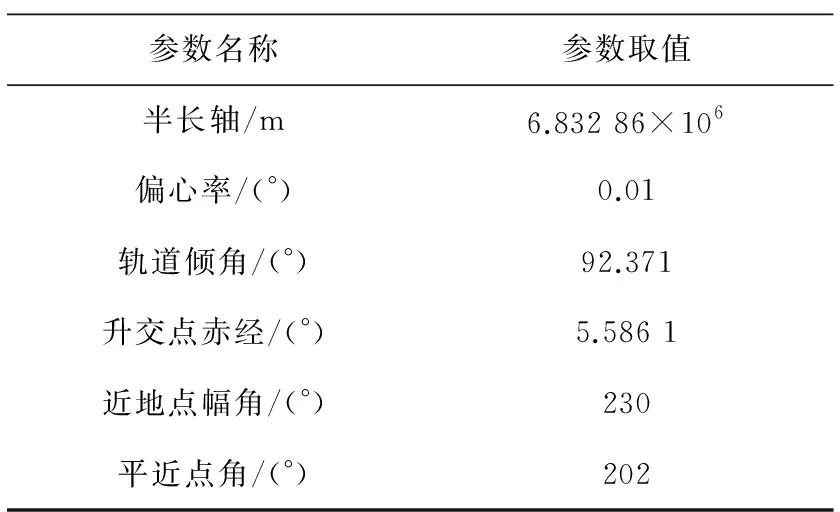
表1 低軌用戶軌跡初值設置Tab.1 Initial value setting of LEO user track
地球重力場選用70階EGM96模型,不考慮固體潮影響;大氣密度計算選用NRLMSISE2000模型;太陽光壓選用圓柱地影模型;考慮太陽和月球的三體引力影響,選用JPL的DE405星歷計算日月位置;考慮相對論效應。
4.2 仿真結果及分析
本次仿真的軌跡與STK10.0軟件仿真軌跡比較結果顯示,經過統計24 h后其三維位置誤差保持在10.0 m之內,速度誤差保持在0.012 m/s之內。
三維位置誤差分布如圖2所示,三維速度誤差分布如圖3所示。
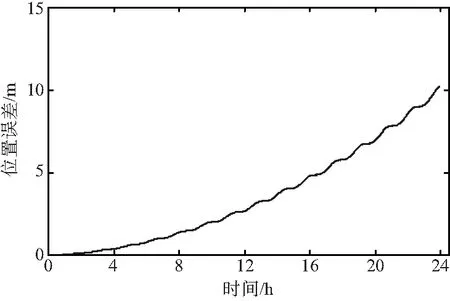
圖2 三維位置誤差分布Fig.2 Error distribution graph of three-dimensional position
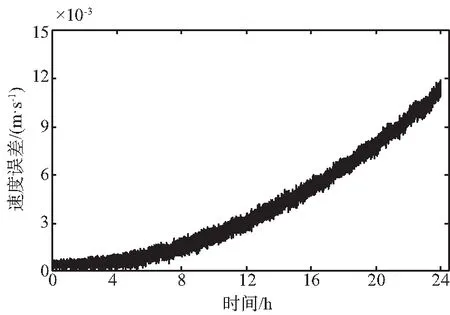
圖3 三維速度誤差分布Fig.3 Error distribution graph of three-dimensional velocity
通過上述測試結果分析,低軌用戶軌跡仿真精度能到達較高水平,典型攝動力模型下逼近國外STK10.0軟件軌道仿真精度水平。因此,該仿真算法在逼真性和可靠性上完全可以滿足衛星導航模擬器數學仿真的需要。
5 結束語
在調研國內外已有軌跡仿真技術方案的基礎上,結合衛星導航模擬器應用實際需求,深入研究了低軌用戶軌跡仿真的數學模型,確定了低軌用戶軌跡仿真的算法,完成了低軌用戶軌跡仿真的流程設計與軟件實現。經過仿真與分析,低軌用戶軌跡仿真軟件與STK10.0軟件的仿真結果偏差小于10 m,達到了很高的精度,提升了衛星導航模擬器的性能,有力支持了低軌衛星地面驗證工作。

