不同重連概率的小世界脈沖神經網絡抗擾功能研究*

郭 磊，馮 海，石洪溢

(1.天津市生物電工與智能健康重點實驗室(河北工業大學),天津 300130;2.省部共建電工裝備可靠性與智能化國家重點實驗室(河北工業大學),天津 300130)

1 引言

隨著電磁環境的日益復雜，各種電磁干擾對電子系統造成的不良影響越來越嚴重，這使得傳統電磁抗擾方式不足的問題日漸突出。電磁仿生學[1,2]的概念由此被提出，目的是學習和借鑒生物體的優良特性，以期建立全新防護模式。

生物體在神經系統的調節下呈現出的自適應抗干擾能力是非生物體無法比擬的，而這一能力與突觸可塑性的調控密切相關。突觸可塑性分為興奮性和抑制性2種，興奮性突觸可塑性以往是研究的重點[3]，而抑制性突觸可塑性的調控作用也逐漸被人所重視。Kleberg等人[4]證明抑制性突觸可塑性在興奮性和抑制性突觸電導權值的平衡方面起著至關重要的作用。薛曉丹等人[5]在所構建的反饋神經回路模型中發現，在抑制性突觸可塑性的調節下，網絡可取得放電率自穩態。神經網絡自適應抗擾功能的研究是近年來的熱門問題，本課題組針對這一問題的研究現狀，開展了基于層級脈沖神經抗擾功能的研究工作[6,7]，前期工作成果有：揭示了生物體的自適應抗干擾能力與突觸可塑性機制有關；網絡在損傷條件和噪聲環境下具有一定的抗擾功能和抗擾范圍。王美麗等人[8]在構建的反饋神經回路模型中發現，網絡在抑制性突觸可塑性的調控下，對外加噪聲刺激具有較強的魯棒性。拓撲結構是網絡的關鍵特性，目前關于神經網絡抗擾功能的研究主要是基于層級網絡，而復雜網絡更符合生物真實性。

大量研究表明，腦網絡具有顯著的小世界屬性[9,10]，小世界網絡模型中重連概率參數對其自身網絡特性有明顯的影響[11]，進一步研究小世界模型的參數對神經網絡的抗擾功能的影響具有重要意義。本文構建了興奮性和抑制性突觸可塑性共同調節的小世界脈沖神經網絡，研究了不同重連概率的網絡在高斯白噪聲刺激下的抗擾功能。

2 小世界脈沖神經網絡的構建

本文基于小世界網絡拓撲，以Izhikevich神經元模型為節點，以突觸可塑性模型為連接關系構建了小世界脈沖神經網絡。

2.1 小世界網絡的生成及其特性分析

WS(Watts-Strogatz)小世界網絡的生成算法為：生成節點數目為500的環形規則網絡，每一節點與其鄰近的各10個節點連接；從第1個節點開始，對其連邊以重連概率p進行連接，p取值為0～1。本文通過實驗確定生成重連概率p為0.2,0.4,0.6,0.8的小世界網絡，基于復雜網絡特性理論對比分析各網絡拓撲特性。

(1)平均聚類系數。

聚類系數的描述如下所示：

Ci=2ei/(ki(ki-1))

(1)

其中，ei表示節點間實際相互連接的邊數，ki表示節點所有相鄰節點的個數，ki(ki-1)/2表示節點間最多可能相互連接的邊數。平均聚類系數為網絡中所有節點聚類系數的平均值，其描述如下所示：

(2)

其中，N表示節點的數目。平均聚類系數表征網絡中節點連接的集團化程度和信息傳輸能力，平均聚類系數越大，網絡整體的信息傳遞能力越強。在圖1中，隨重連概率的增大，網絡平均聚類系數明顯減小，說明該系數受重連概率的影響較大。

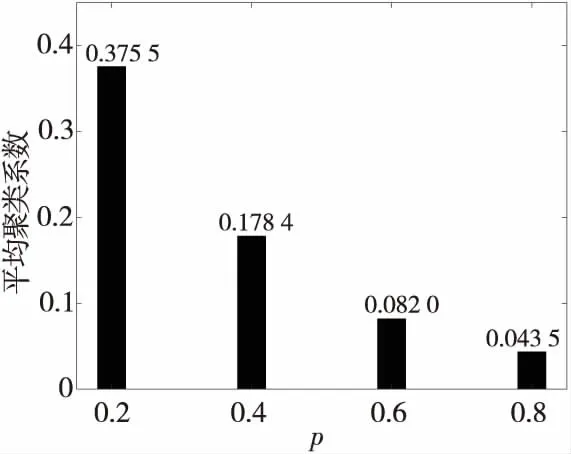
Figure 1 Average clustering coefficient under different rewiring probabilities圖1 不同重連概率下的平均聚類系數

(2)平均路徑長度。

平均路徑長度是表示網絡信息傳遞效率的指標，其值越小代表相應的效率越高，其描述如下：

(3)

其中，dij表示2節點間的距離,V為網絡中所有神經元的集合。

在圖2中，小世界網絡的神經信息傳遞效率隨重連概率的增大有較小幅度的增大，網絡的平均路徑長度受重連概率的影響較小。

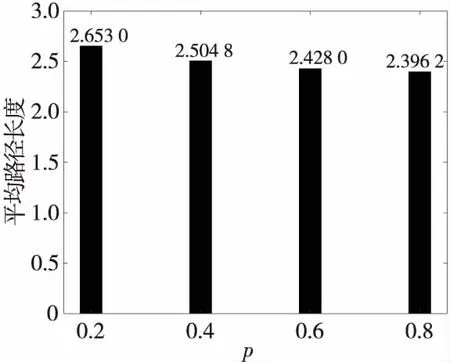
Figure 2 Average path length under different rewiring probabilities圖2 不同重連概率下的平均路徑長度

(3)全局效率。

全局效率是表示網絡信息傳遞效率的指標，其值越大代表相應的指標越好，其描述如下所示：

(4)

在圖3中，小世界網絡的神經信息傳遞效率隨重連概率的增大有較小幅度的增大，說明網絡的全局效率受重連概率的影響較小。

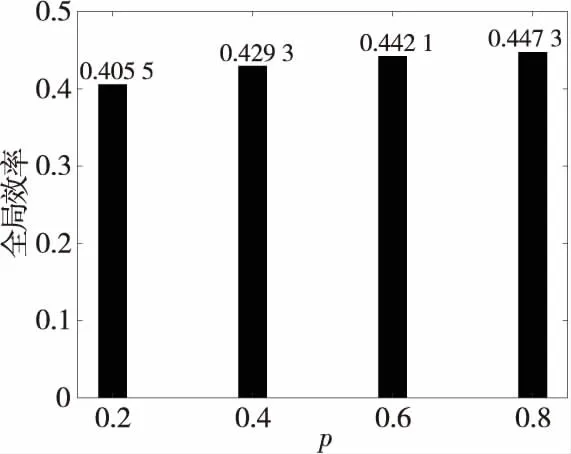
Figure 3 Global efficiency under different rewiring probabilities圖3 不同重連概率下的全局效率

(4)小世界屬性。

小世界屬性可以定量分析小世界網絡的屬性，其描述如下所示：

σ=γ/λ

(5)

其中，γ表示小世界網絡與隨機網絡平均聚類系數之比，λ表示小世界網絡與隨機網絡的平均路徑長度之比。σ>1的網絡表示其具有小世界屬性。σ值越大代表其相應的屬性越強。

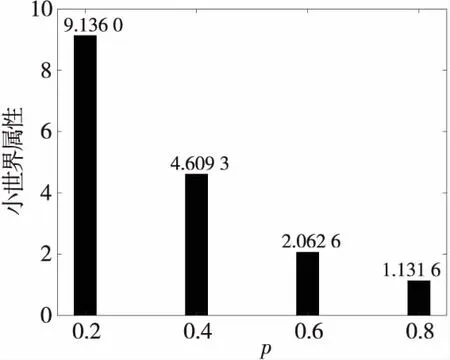
Figure 4 Small world attributes under different rewiring probabilities圖4 不同重連概率下的小世界屬性

在圖4中，小世界網絡的小世界屬性隨重連概率的增大明顯減小，說明網絡的小世界屬性受重連概率的影響較大。

小世界網絡具有高聚類系數和低平均路徑長度的特性，由于各網絡拓撲特性受重連概率的影響的不同，從損失較小平均路徑長度和全局效率而獲得較大的平均聚類系數和小世界屬性的角度考慮，較低的重連概率，可較好地滿足小世界網絡特性。

2.2 Izhikevich神經元模型

Izhikevich神經元模型的優勢是適合計算機仿真，且趨近生物真實放電特征，其描述如下所示：

dv/dt=0.04v2+5v+140-u+I，

du/dt=a(bv-u),

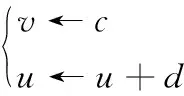
(6)

其中，v表示神經元膜電位；u表示膜電壓恢復變量；I表示輸入電流和突觸電流的總和，a,b,c,d為4個無量綱參數。興奮性神經元采用規則放電模式RS(Regular Spiking)，其參數設置為：a=0.02,b=0.2,c=-65,d=8，放電特性如圖5a所示；抑制性神經元采用低閾值放電模式LTS(Low-Threshold Spiking)，其參數設置為：a=0.02,b=0.25,c=-65,d=2，放電特性如圖5b所示。興奮性和抑制性神經元選擇這2種放電模式是因其在生物中常見且具有代表性[12,13]。圖5中，橫縱坐標分別為仿真時間和神經元膜電壓。

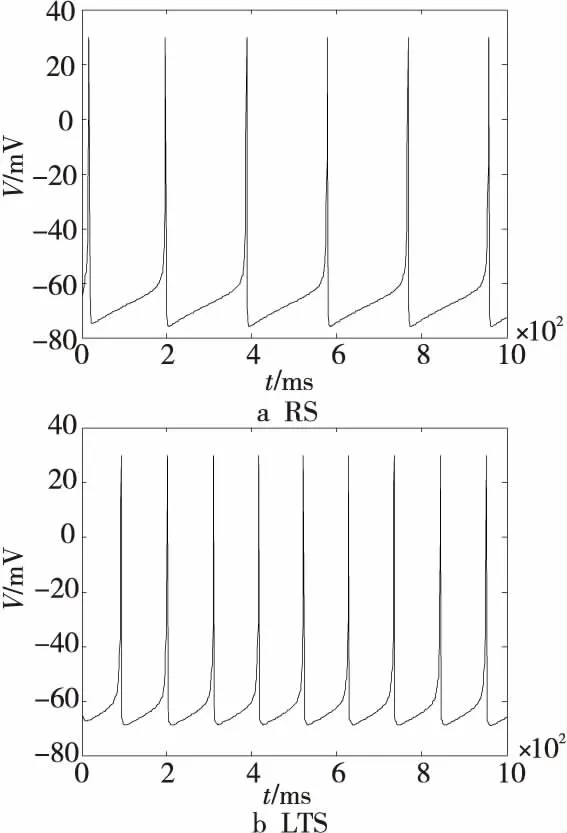
Figure 5 Firing mode of Izhikevich neuron圖5 Izhikevich神經元放電模式

2.3 突觸可塑性模型

突觸可塑性模型描述如下：

Isyn=gsyn(t)(V-Vm(t))

(7)

其中，Isyn表示突觸電流；gsyn(t)表示突觸權值；Vm(t)表示突觸后神經元的膜電位；V表示反轉電位，興奮性突觸的反轉電位VE=0 mV；抑制性突觸的反轉電位VI=-70 mV。具體調節規律：

(1)當突觸前神經元i的動作電位未傳遞到突觸后神經元j時，相應突觸權值會發生指數衰減，其描述如下所示：

興奮性：

(8)

抑制性：

(9)

其中，gex和gin分別表示興奮性和抑制性突觸權值；τex和τin分別表示興奮性和抑制性突觸權值的衰減常數，設定τex=τin=5 ms;t表示時間。

(2)當突觸前神經元i的動作電位傳遞到突觸后神經元j時，調控規律描述如下：

興奮性：

(10)

抑制性：

(11)

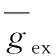
(12)

(13)

其中,Δt表示突觸前后神經元放電間隔時間；τ+和τ-表示突觸增強和減弱時突觸前后神經元放電時刻間隔范圍，τ+=τ-=20 ms；A+和A-為興奮性突觸電導在增強和減弱時的最大修正值；B+和B-為抑制性突觸電導在增強和減弱時的最大修正值。A+=0.1,A-=0.105；B+=0.02,B-=0.03。

本文以重連概率分別為0.2,0.4,0.6,0.8，節點規模均為500的WS小世界網絡拓撲，以Izhikevich神經元模型為節點，基于興奮性和抑制性突觸可塑性模型構建4個網絡拓撲的脈沖神經網絡。依據神經解剖學實驗結果，網絡中興奮性神經元和抑制性神經元的比例為4∶1[14]。

3 高斯白噪聲刺激下網絡的抗擾功能分析

本文以放電率和膜電位相關性作為抗擾指標對比分析了不同重連概率的小世界脈沖神經網絡的抗擾功能。

3.1 高斯白噪聲

現實生活中如雷達和通訊系統等電子系統中的噪聲形式多為高斯白噪聲，因此以高斯白噪聲為噪聲環境研究抗擾功能具有重要的現實意義。高斯白噪聲ξ(t)滿足：

〈ξ(t)〉=0

(14)

〈ξi(t),ξj(t′)〉=Dδijδ(t-t′)

(15)

其中，ξi(t),ξj(t′)為神經元i,j的噪聲干擾項，D為噪聲強度，當i=j(t=t′)時，δij=1(δ(t-t′)=1);否則，δij=0(δ(t-t′)=0)。高斯白噪聲為電流刺激，實驗時將ξ(t)施加到式(6)的電流部分得到高斯白噪聲下脈沖神經網絡模型。

3.2 不同重連概率的網絡抗擾功能對比性分析

3.2.1 基于放電率網絡抗擾功能的分析

放電率為單位時間內神經元脈沖發放次數。本文中的放電率取網絡中的平均值。為了定量計算干擾前后放電率的變化，引入放電率的相對變化率，其描述如下所示：

δ=((fj-fi)/fi)*100%

(16)

其中，fi表示干擾前網絡的放電率，fj表示干擾后網絡的放電率，δ表示干擾前后放電率的相對變化率。通過計算干擾前后放電率的相對變化率分析不同重連概率下小世界脈沖神經網絡抗擾功能。

以放電率作為不同重連概率下的小世界脈沖神經網絡的抗擾指標分析網絡的抗擾功能，對重連概率分別為0.2,0.4,0.6,0.8的小世界脈沖神經網絡中的所有神經元加入強度分別為1 dBW,5 dBW,10 dBW,15 dBW,20 dBW的高斯白噪聲，該噪聲強度是通過實驗取得的，仿真時間為1 000 ms，不同強度的高斯白噪聲刺激下4個網絡拓撲結構的脈沖神經網絡的放電率和放電率的相對變化率的變化趨勢如圖6所示。

在圖6a和圖6b中，橫坐標表示噪聲強度，縱坐標分別表示小世界脈沖神經網絡的放電率和放電率的相對變化率。其中，菱型折線、方型折線、十字型折線、三角型折線分別表示重連概率為0.2,0.4,0.6,0.8的網絡放電率隨高斯白噪聲的變化情況。由圖6a可知，隨高斯白噪聲強度的逐步增加，各網絡的放電率基本呈現上升趨勢，說明噪聲的強度越大對網絡的作用越強。由圖6b可知：(1)在一定噪聲強度內，各網絡的放電率的相對變化率都較小，說明各網絡對此強度范圍內噪聲的抑制作用較強；超過一定的范圍后，放電率的相對變化率較大，說明各網絡對此強度范圍內噪聲的抑制作用變差。(2)當噪聲強度為1 dBW,5 dBW, 20 dBW時，重連概率為0.2的網絡的放電率的相對變化率最低；當噪聲強度為10 dBW, 15 dBW時，重連概率為0.2的網絡的放電率的相對變化率同樣較低，說明重連概率為0.2的網絡抗擾功能優于其他重連概率的網絡的。

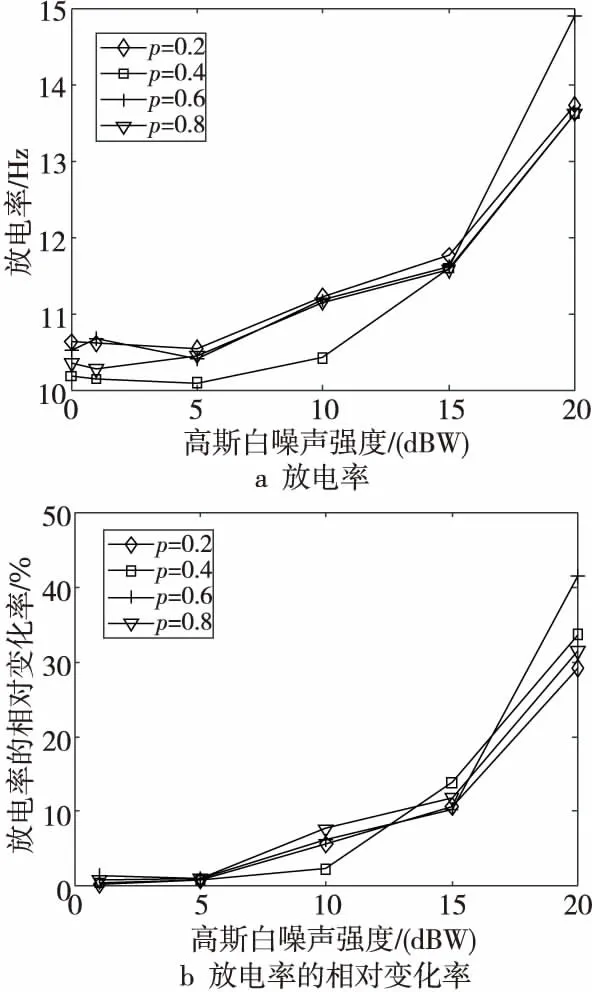
Figure 6 Firing rate varing with the intensity of white Gauss noise圖6 放電率隨高斯白噪聲強度變化

3.2.2 基于膜電位相關性網絡抗擾功能的分析

膜電位相關性可以反映干擾前后神經元膜電位的相似程度。本文通過相關系數計算膜電位相關性，數學表達如下所示：

(17)

其中，xi和xj是高斯白噪聲干擾前后網絡中所有神經元膜電位的平均值，[t1,t2]為仿真時長。

本文通過分析相關系數ρ(τ)的大小來分析網絡的抗擾功能，ρ(τ)越大說明干擾前后神經元膜電位的近似程度越高，其抗擾功能越強。

本文以膜電位相關性作為脈沖神經網絡的抗擾指標分析網絡的抗擾功能，在計算膜電位相關性中干擾前后的膜電位取干擾前后整個網絡中的平均值。對重連概率分別為0.2,0.4,0.6,0.8網絡的所有神經元加入強度分別為1 dBW,5 dBW,10 dBW,15 dBW, 20 dBW的高斯白噪聲，該噪聲強度是通過實驗取得的，仿真時間為1 000 ms，不同強度的高斯白噪聲刺激下4個網絡拓撲結構的脈沖神經網絡的的膜電位相關性的變化趨勢如圖7所示。

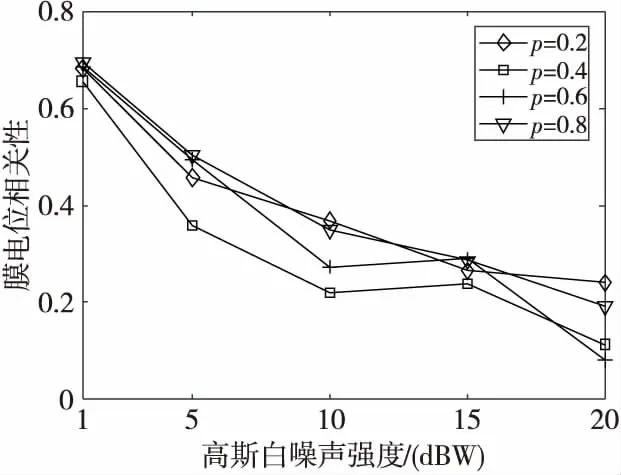
Figure 7 Correlation between membrane potential varing with the intensity of white Gauss noise圖7 膜電位相關性隨高斯白噪聲強度的變化

在圖7中，橫縱坐標分別表示高斯白噪聲強度和小世界脈沖神經網絡膜電位相關性。其中，菱型折線、方型折線、十字型折線、三角型折線分別表示重連概率為0.2,0.4,0.6,0.8的小世界脈沖神經網絡膜電位相關性隨高斯白噪聲的變化情況。由圖7可知：(1)隨高斯白噪聲刺激強度的增大，各網絡的膜電位相關性基本呈下降趨勢，說明噪聲的強度越大對網絡的作用越強。(2)在一定噪聲強度范圍內，不同重連概率的小世界脈沖神經網絡的膜電位相關性較大，說明網絡對此強度范圍內噪聲的抑制作用較強；超過一定的范圍后，各網絡的膜電位相關性較小，說明各網絡對此強度范圍內噪聲的抑制作用變差。(3)在不同重連概率的小世界脈沖神經網絡對比中，重連概率為0.2,0.8的小世界脈沖神經網絡的膜電位相關性基本相當且高于其他重連概率的網絡，說明以膜電位作為抗擾指標，重連概率為0.2,0.8的網絡的抗擾功能優于其他重連概率的網絡的。

綜上所述，基于放電率和膜電位相關性的抗擾指標對比均得出以下一致結論：(1)重連概率的改變對脈沖神經網絡的抗擾功能有影響；(2)最低重連概率0.2的網絡的抗擾功能最優，是由于該網絡的小世界網絡特性最顯著。

4 結束語

本文基于復雜網絡特性理論對比分析了不同重連概率的小世界網絡的拓撲特性；以放電率的相對變化率和膜電位相關性作為抗擾功能的指標，對比分析了4個重連概率的小世界脈沖網絡在高斯白噪聲刺激下的抗擾功能。實驗結果表明，重連概率對平均路徑長度和全局效率值影響較小，而對平均聚類系數和小世界屬性的影響較大，即較低重連概率的小世界網絡損失較小的平均路徑長度和全局效率而獲得較大的平均聚類系數和小世界屬性的角度能夠較好地滿足小世界網絡特性。針對一定強度的高斯白噪聲刺激，基于不同重連概率所構建的小世界脈沖神經網絡均呈現了一定的抗擾能力，且具有較高聚類系數和較低平均路徑長度的脈沖神經網絡的抗擾功能更優良。基于突觸可塑性的突觸權值調節機制是脈沖神經網絡抗擾功能的基礎，重連概率作為小世界網絡的重要參數，較低的重連概率可使小世界網絡具有顯著小世界特性，顯著的小世界特性使該網絡拓撲的脈沖神經網絡具有優良抗擾功能。下一步本課題組將開展基于FPGA脈沖神經網絡構建及抗擾功能的硬件實現的研究工作。