模態求解中的若干問題研究

周利 王志偉 楊敏

摘 要：機械結構不僅需要有良好的靜態承載能力，還需要有優異的動力學性能。模態分析是結構線性動力學的分析基礎，文章采用有限元法針對影響模態分析精度的預應力（螺栓預緊力和壓力容器）、摩擦系數、介質（液體或者氣體）、網格粗糙度進行了詳細的對比分析，結果表明模態對較小的預應力以及摩擦系數更加敏感，濕模態頻率比采用質量點法計算的頻率模態較低，當單元尺寸較小時，模態頻率變化不明顯，當單元尺寸超過某一限度時，模態頻率出現丟失甚至錯誤。

關鍵詞：模態分析;預應力;摩擦系數;虛擬質量法;單元尺寸

中圖分類號：U467? 文獻標識碼：B? 文章編號：1671-7988（2020）13-164-05

Research on Several Problems in Modal Solution

Zhou Li1， Wang Zhiwei2， Yang Min1

（ 1.Shaanxi Automobile Group.， Ltd.， Technical Center， Shaanxi Xi'an 710200;

2.Shaanxi Heavy Duty Automobile Co.， Ltd.， Shaanxi Xi'an 710200 ）

Abstract： Mechanical structures not only need to have good static carrying capacity， but also have excellent dynamic performance. Modal analysis is the basis of structural linear dynamics， In this paper， the influence of prestress （bolt pretension force and pressure vessel）， coefficient of friction， medium （liquid or gas）， mesh roughness on modal analysis accuracy is studied by finite element method. The results show that the modal mode is more sensitive to the smaller prestress and friction coefficient， the wet modal frequency is lower than the frequency mode calculated by mass point method， the modal frequency change is not obvious when the element size is small， and the modal frequency is lost or even wrong when the element size exceeds a certain limit.

Keywords： Modal analysis; Prestress; Coefficient of friction; Virtual mass; Element size

CLC NO.： U467? Document Code： B? Article ID： 1671-7988（2020）13-164-05

前言

模態分析是結構分析的重要內容，在航空航天、汽車、輪船、電子電器等行業是必須考察的重要項目。模態分析是動力學分析的基礎，比如在進行頻率響應分析、隨機響應分析、響應譜分析之前，必須先進行模態分析;模態分析也是減震隔振的重要依據，通過比較模態頻率而避免產生共振;模態分析還可以用于指導試驗，如幫助確定加速度計的最佳安裝位置、監測結構疲勞壽命、用于有限元模型與試驗結果的對標等。

模態包含頻率和振型，每一階模態對應著特定的振型，頻率和振型表征了結構的固有屬性，主要與結構的質量分布和剛度分布有關，影響質量分布的因素有材料密度、結構形狀、質心坐標等，影響剛度分布的因素有邊界條件、結構形狀、材料彈性模量、接觸等。陳長盛等[1]研究了螺栓連接對結構模態以及傳遞特性的影響，發現當預緊力一定時，固有頻率隨著螺栓剛度的提升增大。伍濟鋼等[2]發現如果摩擦系數的變化引起了模態參數的有效剛度，那么摩擦系數對該階模態的影響就較大，反之就很小。梁建術等[3]發現，流固耦合作用對波紋管固有頻率有較大影響，為管道振動提供了重要的動力學依據。本文將研究影響模態的常用幾個因素：預應力（螺栓預緊力、壓力容器壓力）、摩擦系數、液體介質的簡化以及單元尺寸對模態的影響，對有限元建模提高模態分析的精確性具有重要意義。

1 模態基本理論

對于自由度為N的無阻尼系統的振動，其自由振動的微分方程為：

（1）

式中：M為質量矩陣;K為剛度矩陣;X為位移向量。對上述方程進行拉式變換，得到：

（2）

對于時不變系統，s=jw，帶入上述方程（2）中得到：

（3）

為了將上述方程解耦，通過模態矩陣，建立物理坐標與模態坐標的關系，為：

（4）

式中?為由各階模態組成的模態矩陣，Q為模態坐標矩陣。將4式帶入3中，并且在方程兩邊乘以得到?T，得到方程為：

（5）

式中， Mr、Kr為模態坐標下的模態質量矩陣和剛度矩陣，均為對角陣。對于第i階模態，其表達式為：

（6）

式中，Mr，i、Kr，i為第i階模態質量和模態剛度，w為對應的角頻率，w/2π即為對應的自然模態頻率。

2 預應力對模態的影響

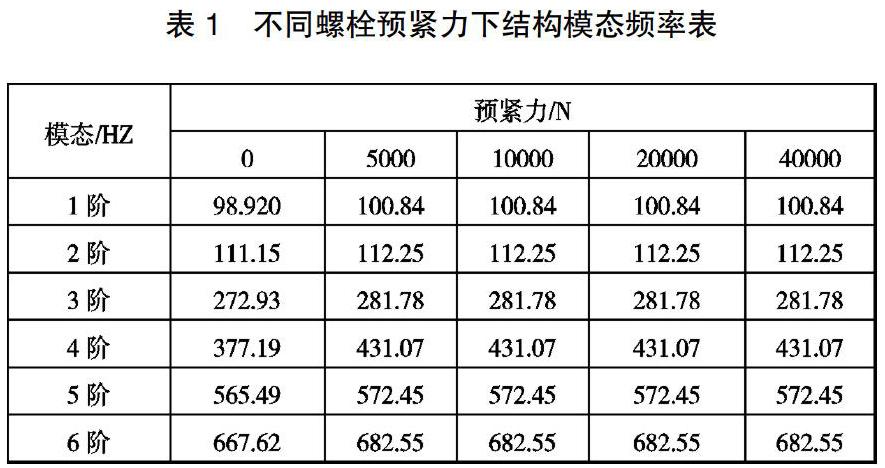
本文采用有限元方法對結構進行建模，前處理軟件采用HyperMesh，求解器為OptiStruct，后處理軟件采用Hyper View。模型為某車型用油罐支架，截取一段車架縱梁。由于縱梁和油罐支架均為薄板構件，將上述支架抽中面并劃分為平均單元尺寸為8mm的網格單元，主要為四邊形單元和少量三角形單元。為簡化計算，將螺栓簡化為兩端抓取一圈rbe2單元中間通過截面半徑為16mm的結構，預緊力通過一維梁單元施加。在油罐支架的內表面與車架縱梁的外表面建立接觸對，油罐支架的內表面為從面，車架縱梁外表面為從面，設定接觸為滑動摩擦，接觸摩擦系數為0.3;為了橫向對比，將預緊力分別設定為0N、50000N、10000N、20000N、40000。約束縱梁兩端節點全部自由度，便于計算比較，僅計算結構的前六階模態。有限元仿真模型如圖1，首先對螺栓施加預緊力，進行非線性靜力學分析，計算完成后，將施加預緊載荷后結構的剛度矩陣傳遞到后續的模態分析中，即將非線性分析的最后結果作為模態分析的基態，預緊力為0N時的模態振型如圖2所示。

經過計算發現，預緊力的施加對模態振型的影響并不顯著，但是對頻率的影響如表1所示，預緊力由0增加到5000N時，第一到第六階模態均有較大幅度的增加，并且階次越高，頻率增加的幅度越大，高階次模態對螺栓預緊力更加敏感;預緊力從5000N增加到40000N過程中，第1到6階頻率基本沒有變化，這說明模態頻率對較小的預緊力更加敏感。壓力容器的中預壓力對模態影響的研究方法、原理和過程類似，這里不做詳細介紹。

3 摩擦系數的影響

采用上述油罐支架縱梁模型，由于模態對較小的預緊力更加敏感，所以設定所有的螺栓預緊力為5000N，設定摩擦系數依次為0、0.2、0.4、0.6、0.8以及綁定接觸，試驗結果如表2所示。當摩擦系數由0增加到0.2時，前六階模態振型未發生變化，模態頻率發生了明顯變化，模態階次越高，模態頻率變化的幅值越大，尤其是第四階模態頻率發生了顯著的變化。當摩擦系數由0.2增加到0.4時，模態振型無變化，模態頻率出現了微小的幅度的降低。當模態系數由0.4增加到0.8時，模態振型不變，模態頻率無變化，可見當摩擦增加到一定數值時，模態頻率不在受到影響。當采用綁定連接時，模態頻率顯著高于其它摩擦系數下的頻率。由此可以判斷，隨著摩擦系數的增加，模態頻率隨之增大，模態階次越高，對摩擦系數越敏感;當摩擦系數增加到一定值是，模態頻率不在隨著摩擦系數發生變化;綁定連接顯著的增大了接觸面的剛度，顯著的影響模態頻率。

4 介質

在許多實際的結構中，既有液體也有固體，比如液體火箭發動機、汽車燃油箱、水中的輪船等，為了簡化計算，通常在有限元建模時采用質量點的方式代替液體，然后用rbe3單元將質量點與單元節點連接。然而通過與試驗結果對比發現，這種簡化方式造成求解的模態與實際測試結果偏差較大，為后續的動力學求解造成較大基礎誤差。為了解決這一問題，陳偉等[4]采用聲固耦合的方法研究了流固耦合模態，但是付廣等[5]發現，目前考慮流體的方法中，虛擬質量法的精度最高，本文采用虛擬質量法計算流固耦合模態，探討不同液面高度時，與質量點法計算的模態的差異。

虛擬質量法主要用來考慮水動力效應對結構響應的影響，液體會在濕表面產生附加質量，該質量不是流體的實際質量，而是等效附加質量，該方法不需要對流體區域劃分流體網格。該方法假定流體無粘、無旋、不可壓縮。具有統一的密度，自由面壓強為零，不考慮重力，晃蕩頻率低于結構的基頻，并且不考慮非線性效應和氣彈效應。

由Helmholtz和Laplace方程可以求得速度勢和壓力場：

（7）

（8）

式中：

ui—任意節點ri的速度向量;

Aj —結構表面上某微元的面積;

σj—節點rj處的單位面積體積流量向量;

eij—從點i到j點的單位向量;

pi—任意面Aj上的壓力;

ρ—流體密度。

由上式可得矩陣x和Λ，故：

（9）

（10）

式中F為節點壓力，根據力矩陣、質量矩陣與加速度矩陣之間的關系：

（11）

聯合可求得虛擬質量矩陣為：

（12）

流體以虛擬質量矩陣出現在耦合方程中，耦合方程可表示為：

（13）

式中：

M—結構質量矩陣;

MA—流體虛擬質量矩陣;

K—結構剛度矩陣;

KA—流體對結構的剛度矩陣。

一般情況下，KA與結構自身剛度相比較小，可以忽略。由上式可計算出基于虛擬質量法的耦合特征值。

本算例采用長、寬、高均為100mm的頂部開口的箱體，箱體壁面厚度為1mm;將箱體抽中面，用四邊形單元劃分，單元尺寸為5mm，約束箱體的底角四個節點自由度123456，模型如圖3所示。為了研究的便利性，分別計算當液面高度h為箱體高度的1倍、0.5倍、0.25倍時結構的模態，采用質量點法和虛擬質量法考察模態變化規律。

由表3可見，相同高度液面下，采用虛擬質量法計算的結構模態比采用質量點法計算的結構模態普遍較低，隨著液面高度的降低，差距逐漸縮小。

5 網格粗糙度的影響

由公式6可知，對于多自由度系統，通過有限元離散成有限數量節點，節點自由度的多少決定了模態階次和振型;影響節點自由度的主要因素有單元的形狀、單元尺寸、單元階次等，常用單元形狀三角形單元、四面體單元、四面體單元、六面體單元、三棱柱單元等，常用的單元階次為1階單元和二階單元。在實際使用過程中，鈑金件應用非常廣泛，尤其在汽車結構中，以三角形和四邊形單元混合建模較為常見。

本算例采用長100mm、寬1mm、厚0.2mm的薄板件，約束零件的兩端自由度123456。分別采用單元尺寸為1mm、5mm、10mm、20mm、50mm劃分零件，為了方便對比，只考察結構的前6階模態頻率和振型。如表4和表5所示，網格尺寸為1mm、5mm、10mm時，前3階模態頻率相差不大，但是第4、第5和第6階模態頻率差異變大。當單元尺寸增加到20mm，振型基本保持不變，但是頻率已經與上述的三種單元尺寸相差較大，隨著模態階次的提高，差異更加明顯。當單元尺寸增加到50mm時，模態振型出現顯著改變，尤其是當單元尺寸為50mm時，振型已經和單元尺寸為1mm、5mm、10mm、20mm時完全不同，模態頻率相差數十倍，并且隨著階次的增加差異更加明顯。由于模型的對稱性，當單元尺寸為1mm時，模型的第一階模態和第二階模態振型和頻率基本相同，實際可以認為是同一階模態，但是隨著單元尺寸的增加，振型仍然為對稱狀態，但是頻率已經有較大差異。此可見，當單元尺寸為1mm、5mm、10mm，模態頻率和振型差異不明顯，即模態對網格尺寸不敏感，但單元尺寸增加為20m時振型基本一致，但是頻率已經發生了較大的變化單元為50mm時，模態和振型均發生顯著差異;即模態對網格已經非常敏感。

6 結論

本文采用有限元法研究了預應力（螺栓預緊力和壓力容器）、摩擦系數、介質（液體或者氣體）、網格粗糙度對模態分析精度的影響，結果表明：結構模態對較小的預緊力更加敏感;隨著摩擦系數的增加，模態頻率隨之增大，當摩擦系數增加到一定值時，模態頻率不再隨著摩擦系數發生變化;相同高度液面下，采用虛擬質量法計算的結構模態比采用質量點法計算的結構模態頻率低，隨著液面高度的降低，差距逐漸縮小。當網格尺寸較小時，模態對網格尺寸不敏感，當網格尺寸較大時，模態頻率和振型出現明顯變化，當網格尺寸超過一定范圍時，會導致模態失真甚至錯誤。

參考文獻

[1] 陳長盛，王強，柳瑞鋒，李國平，周璞.螺栓連接對結構模態及傳遞特性影響研究[J].振動與沖擊，2014，33（02）：178-182.

[2] 伍濟鋼，邵俊，周根，陽德強.摩擦系數對螺栓聯接機匣模態頻率的影響研究[J].噪聲與振動控制，2020，40（01）：5-8+18.

[3] 梁建術，蘇強，李欣業.基于ANSYS/Workbench流固耦合輸液波紋管的模態分析[J].機械設計與制造，2013（02）：91-93.

[4] 陳偉.水下結構流固耦合及聲輻射數值方法研究[D].華中科技大學，2009.

[5] 付廣，梁靜強，羅慧娟，等.汽車燃油箱流固耦合模態分析[J].汽車科技， 2016（2）：25-28.