基于轉爐干法除塵系統的煙氣溫度控制策略

田 海，郭林威，閆兆陽，姚震宇

（內蒙古科技大學 信息工程學院，包頭014010）

在轉爐煉鋼過程中，噴槍向熔池通入的氧氣與鐵水反應，產生大量的熱量和煙氣，煙氣中混入鐵和鐵的氧化物顆粒及原料中的其它微粒，隨意排放轉爐煙氣會嚴重污染環境，目前轉爐煙氣凈化主要有干法除塵和濕法除塵兩種，相對于濕法除塵，干法除塵具有效率高、 除塵后獲得的煤氣熱值高、系統簡化等優點。

實現煙氣溫度的合理有效控制，不但可以達到較好的除塵效果，而且降溫后的煙氣進入靜電除塵器可保證靜電除塵器安全可靠工作[1]。干法除塵系統的有效運行是轉爐煉鋼正常進行的前提，對穩定工況有重要意義。

轉爐煙氣溫度控制一般采用相關公式法結合PID 調節的控制策略，但因實際煙氣流量計算存在誤差，造成煙氣溫度波動較大。為提高煙氣控制效果，本文提出一種控制策略：首先用實驗建模的方法建立起轉爐干法除塵系統中溫度的數學模型，然后采用模糊自適應PID 控制方法對煙氣溫度進行控制，并在Matlab/Simulink 平臺下仿真，驗證控制效果。

1 干法除塵工藝過程

在轉爐氧槍吹氧，與鐵水發生反應過程中產生的煙氣溫度約為1500 ℃，煙氣由爐口處的煙罩捕獲，經煙罩進入冷卻煙道，煙氣被冷卻到900 ℃左右進入蒸發冷卻器，根據煙氣的溫度控制噴水量，為達到更好的除塵降溫效果，在通入冷卻水的同時通入蒸汽將冷卻水霧化，霧化的水滴經煙氣中的熱量蒸發，從而起到冷卻煙氣的作用，精確控制噴水量使蒸發冷卻器出口處的煙氣溫度降到230 ℃～310 ℃。噴射的冷卻水和蒸汽也使煙氣變得濕潤利于煙塵的凝聚，凝聚的大顆粒煙塵受重力下落，再經粗灰輸送機構輸出，此時煙氣中30%～50%的煙塵被除去。下一步煙氣進入圓筒形靜電除塵器，除塵器首先對煙塵充分荷電，荷電后的煙塵在電場力作用下到達陽極板，然后被振打器敲落再由刮灰機刮落，通過細灰輸送機構輸出，經過電除塵器的煙氣，其煙塵含量低于10 mg/m3。除塵后的煙氣進入到切換站，若煙氣符合回收條件，其在煤氣冷卻器進行冷卻后送至煤氣柜儲存，若不符合回收條件則通過放散煙囪點火放散，其工藝流程如圖1 所示。

經蒸發冷卻器處理的煙氣溫度要求控制在200 ℃～300 ℃，若煙氣溫度過低，進入靜電除塵器的潮濕煙塵易粘結在一起附在陰極線上，導致陰極線肥大，使除塵電場放電頻繁，嚴重腐蝕電場內設備；若煙氣溫度過高，煙塵的電阻率升高，靜電除塵器的工作效率下降，導致排放的煙氣含塵量增多。

為穩定蒸發冷卻器出口處的煙氣溫度，除加強設備維護管理外，還需要優化工藝，在影響煙氣溫度的諸多因素中，冷卻水流量的控制最為重要，因此準確控制冷卻水的流量是穩定蒸發冷卻器出口煙氣溫度的關鍵。

2 煙氣溫度控制系統建模

為了便于研究蒸發冷卻器對煙氣溫度的控制情況，確定控制參數，需要建立相關數學模型。

2.1 溫度模型的建立

在影響煙氣溫度的各種控制量中，噴水量是最主要的因素，為研究方便，建立以噴水閥門開度為輸入量，經蒸發冷卻器處理的煙氣溫度為輸出量的數學模型。若直接采用連續模型辨識，模型擬合效果較差，故先選擇離散模型進行辨識，再將離散模型連續化，轉換為連續模型[2]。應用機理模型和測試建模相結合的方式，先通過機理得出系統的模型類，然后將測試建模得到的高階離散傳遞函數轉換為連續模型再化歸為所需的機理模型類，這樣得到的模型既保證了一定的精確度，又簡化了模型結構，便于控制。

2.1.1 機理模型

蒸發冷卻器出口煙氣溫度采用相關文獻中由機理分析獲得的模型[3]：

式中：G（s）為建立的系統模型；K 為冷卻水閥門開度的增益；Td為冷卻水閥門開度的純滯后時間；Tp1為冷卻水閥門的時間常數；Tp2為蒸發冷卻器入口煙氣流動速度的時間常數。

2.1.2 辨識模型的建立

系統辨識參數有多種方法，其中最小二乘法可以在最小方差意義上得到一個與實驗數據擬合度最高的數學模型，所得到的結果具有無偏性、有效性、一致性。采用Matlab R2016b 中的系統辨識工具箱進行辨識，該工具箱辨識算法采用最小二乘法。圖2 為系統辨識工具箱主頁面及各種處理數據，在Matlab R2016b 主命令窗口中輸入“ident”便可以直接進入工具箱主頁面，對轉爐干法除塵系統進行系統建模的詳細過程如下：

辨識數據的準備辨識對象的輸入數據為某煉鋼廠轉爐的噴水閥門開度，其范圍為0～100；輸出數據為蒸發冷卻器出口的煙氣溫度，溫度范圍為230 ℃～300 ℃，辨識數據一共150 組（數據來源于參考文獻[3]中的附錄）。

數據導入從現場采集到的數據，首先將奇異數據剔除，然后把數據導入到Matlab 工作窗口，在系統辨識工具箱的Import data 下拉列表中導入工作窗口中的數據，數據名為“mydata”，采樣時間為2 s。

對數據預處理工具箱主窗口Preprocess 下有多種預處理方式，選擇對辨識結果影響較大的去除趨勢預處理方式，消除數據中的大畸變。處理后的數據名稱為“mydatad”。將預處理過的150 組數據分為2 組，第一組名為“mydatade”，共90 組，用于辨識參數；第二組名為“mydatedv”，共60 組，用于對辨識數據的驗證。

圖2 系統辨識工具箱主窗口Fig.2 Main window of the system identification toolbox

2.1.3 模型驗證擬合

圖3 即為各模型的擬合度，單擊工具箱主窗口Estimate 下拉列表，選擇Polynomial 模型，對非線性系統選擇其中的ARX 模型，通過設置不同的ARX模型參數可在系統辨識工具箱主頁面得到不同模型，單擊Model output，便可得到各模型的擬合度。

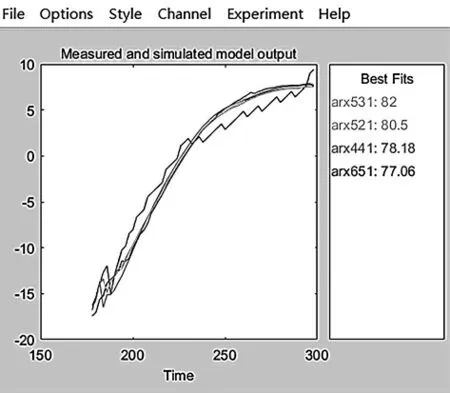
圖3 各模型擬合度Fig.3 Fitting degree of each model

2.2 離散模型連續化與降階處理

擬合度最高的離散模型傳遞函數如式（2）所示，在Matlab 中用函數d2c，將其轉換到s 域上，得到連續的傳遞函數如式（3）。式（3）得到的模型階次較高，參考前文的機理模型，將其進行降階處理，采用帶有時間延遲的次最優降階算法，降階處理后，得到新的控制模型如式（4）所示。

式中：G1（z）為離散系統傳遞函數模型。

式中：G2（s）為離散系統傳遞函數連續化的連續系統函數模型。

式中：G3（s）為降階后得到的最終傳遞函數模型。

為檢驗降階模型的準確性，對原模型和降階模型做單位階躍響應和伯德圖曲線，分別如圖4、圖5所示，可見采用帶有時間延遲的次最優降階算法得到的降階模型可以很好地逼近原模型。

圖4 原模型和降階模型的階躍響應曲線Fig.4 Step response curves of original model and reduced order model

圖5 原模型和降階模型的伯德圖Fig.5 Bode diagram of original model and reduced order model

3 煙氣溫度控制算法

控制蒸發冷卻器出口的煙氣溫度在符合要求的范圍內，需采用合理的控制方式對蒸發冷卻器噴射的冷卻水流量和蒸汽流量進行控制。

3.1 控制策略

在轉爐吹煉階段，煙氣流量和溫度相對平穩，蒸汽流量可取固定值，只考慮對煙氣溫度影響較大的冷卻水流量的控制[1，4]。傳統的PID 控制其控制參數無法在線整定，煙氣溫度調節不穩定，對后續除塵工序不利。為提高控制效果引入模糊自適應PID控制方式，模糊自適應PID 可根據煙氣溫度設定值和實際值的偏差及偏差變化率自動調整控制參數，有效抑制煙氣流量變化等因素對溫度調節的干擾，具有更好的控制性能。

3.2 模糊自適應PID 控制器的構造

模糊自適應PID 控制器由模糊控制器和PID控制器組合而成，模糊設計可分為如下步驟：

（1）輸入輸出量的選擇及其模糊化；

（2）輸入輸出量的隸屬度函數選擇；

（3）模糊控制規則表的建立；

（4）依據模糊規則表進行模糊推理；

（5）模糊量的清晰化。

公式（5）為系統的控制參數，其中PID 控制器的參數為比例系數kp0、積分系數ki0、微分系數kd0，在本設計中，經過整定三個系數分別取-1.35、-0.0041、-5。模糊控制器的輸出量為比例、積分、微分系數的變化參量Δkp、Δki、Δkd，通過對PID 控制器的參數進行實時修正，由修正后的比例、積分、微分系數kp、ki、kd去控制執行機構，圖6 為控制器的結構框圖。

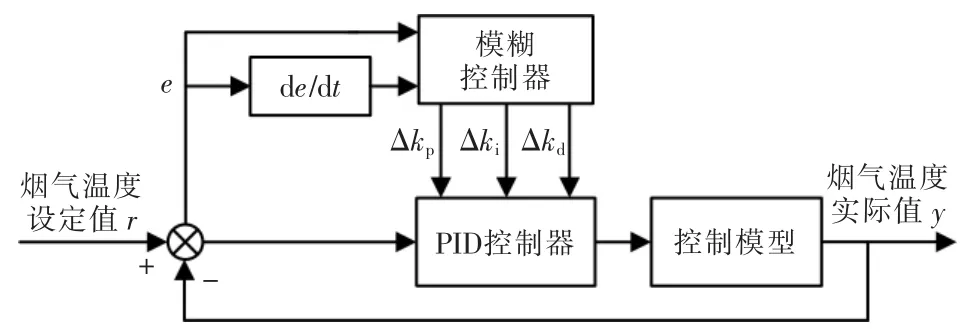
圖6 模糊自適應PID 框圖Fig.6 Fuzzy adaptive PID block diagram

3.2.1 輸入輸出語言變量的確定

模糊控制器以煙氣溫度的實際值和設定值的差值及差值變化率作為輸入值，基本論域分別取［-13 5］、［-20 6］，定義輸入語言變量“誤差E”、“誤差變化率EC”作為各自的模糊量；輸出量為比例、積分、微分系數的增量Δkp、Δki、Δkd，基本論域分別為［-3 0］、［-0.004 0］、［-18 -12］，定義輸出語言變量ΔKp、ΔKi、ΔKd作為各自的模糊量，輸入輸出模糊量的論域均設置為離散整數論域［-3，-2，-1，0，1，2，3］，兩輸入量的量化因子分別取0.33、0.23，三個輸出量的比例因子分別取0.5、0.00067、1。各語言變量語言值均設置為7 檔，即｛NB 負大，NM 負中，NS負小，Z 零，PS 正小，PM 正中，PB 正大｝。輸入語言變量的隸屬度函數選用高斯型，輸出語言變量隸屬度函數選用三角型。

3.2.2 模糊規則庫的確定

可根據控制過程的模糊模型，即通過模糊語言來表述被控過程中的輸入、輸出量關系，得出控制規則。比例系數可提高系統響應速度，但若過大，會產生大的超調；積分系數可消除穩態誤差，但過大會引起積分過飽和； 微分系數可減小系統超調，但過大會增加系統的調節時間。可根據三者對系統響應的影響綜合考慮建立控制規則[5-6]：

（1）若系統存在較大的偏差，需加快響應速度，可加大Kp的取值，Kd取較小值，以避免偏差快速變化出現微分過飽和，Ki取0 或取小值來減小超調引起的積分飽和；

（2）當偏差和偏差變化率大小適中時，為減小超調可使Ki取值適中，Kp取較小的值，同時Kd亦取適中值；

（3）偏差值較小時，Kp，Ki的取值大一些以維持穩態性能，此外當偏差變化率較小時，Kd取值大一些，偏差變化率較大時，Kd取值小一些。

根據上述的控制原則和PID 參數整定情況，可得到模糊控制規則表如表1 所示。

3.2.3 模糊量的清晰化

由模糊推理得到的模糊輸出是模糊子集，需將其轉換為模糊控制器的精確輸出量ΔKp、ΔKi、ΔKd，本文采用重心法求取ΔKp、ΔKi、ΔKd，即對模糊輸出量各元素和對應的隸屬度函數μ 求加權平均值，以求取ΔKp為例，如下式所示：

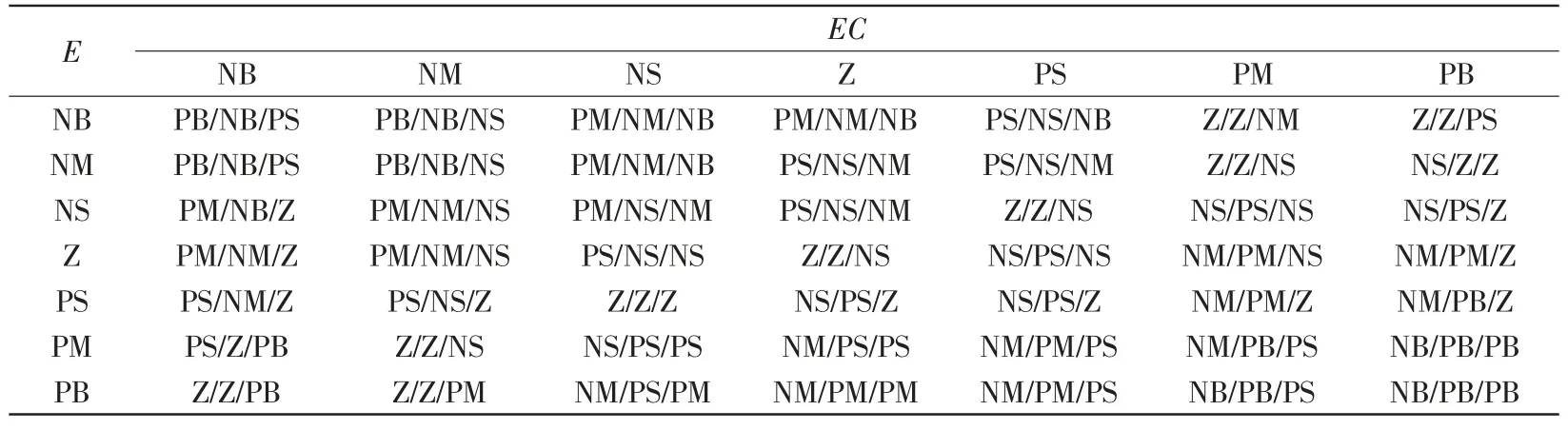
表1 ΔKp、ΔKi、ΔKd 相應的模糊控制規則Tab.1 Fuzzy control adjustment rules corresponding to ΔKp、ΔKi、ΔKd

再將ΔKp、ΔKi、ΔKd轉換為實際作用參數[7]Δkp、Δki、Δkd，以求取Δkp為例，如公式（7）所示：

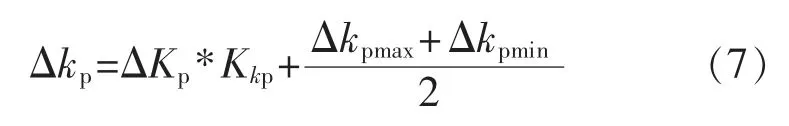
式中：Kkp為Δkp對應的比例因子，Δkpmax和Δkpmin分別為Δkp所取基本論域的上下限。

3.3 仿真結果及其分析

在Matlab/Simulink 中搭建框圖進行仿真，溫度設定值取250 ℃，溫度響應曲線如圖7 所示。

圖7 PID 控制和模糊PID 控制煙氣溫度仿真曲線Fig.7 Simulation curve of flue gas temperature controlled by PID control and fuzzy PID control

由圖可見，采用模糊自適應PID 控制，在PID調節效果的基礎上加快了系統響應速度，且幾乎不產生超調。該控制系統實現了PID 參數的動態整定，優化了系統控制性能。

4 結語

本文針對轉爐干法除塵煙氣溫度的控制要求，對轉爐干法除塵煙氣溫度控制系統進行了深入研究，辨識出了系統的傳遞函數，采用模糊自適應PID控制方式進行控制調節，并在Matlab/Simulink 下進行了仿真對比，仿真結果顯示應用此控制策略，加快了系統響應速度且幾乎消除了超調量。本文僅就主要因素噴水流量對煙氣溫度影響展開討論，為達到更好的煙氣處理效果，還需對影響煙氣溫度的其他因素做進一步研究。