坐底式深水網箱振動實測信號分析處理方法

宋嘎，王娜娜

(1.山東職業學院，濟南 250104；2.煙臺汽車工程職業學院，山東 煙臺 264000)

在實際的深水網箱使用過程中，由于受到復雜的海洋環境影響，結構振動信號復雜多變，往往呈現非穩態信號的特征，同時信號中還會包含有各種噪聲成分，給深海網箱結構的監測帶來了很多難題。在海洋環境中，大多數的測試信號是時變的非平穩信號，僅使用傳統的傅里葉變換進行頻譜分析已經無法滿足實際要求，需要在時域內觀測結構真實模態的變換信息，提高對深水網箱結構實測信號的分析能力,即進行時頻分析[1]。通過時頻分析，可以完整刻畫信號在時間和頻率軸上的能量強度分布——聯合時頻分布[2]，以及結構振動頻率隨時間的變化情況，提供信號的局部特征，從而實現對深水網箱結構的安全檢測[3]。有學者開展的相關研究[4-6]。

本文在傳統變分模態分解的基礎上，通過引入相關性分析及頻域最大值分析，提出一種自適應設置模態階次的變分模態分解方法，根據信號的特征自動確定模態階次。利用Matlab軟件進行編程，并將該方法應用于實測的深海網箱振動信號，證明該方法在處理深海網箱實測振動數據時的有效性及在對深海網箱結構進行安全監測時的應用價值。

1 變分模態分解

變分模態分解可以將非穩定的多成分信號分解為在中心頻率處的有限帶寬成分信號，每個分離出的成分即為有限帶寬的固有模態函數。假設信號y(t)中包含k個分量xk，且每個分量的中心頻率為ωk，各分量通過求解下式的約束變分模型得到：

(1)

式中：*為卷積運算;δ(t)為Dirac分布。

引入拉格朗日乘法算子λ，式(1)可以轉化為非約束變分問題

L({xk},{ωk},λ)=

(2)

式中：α為二次懲罰因子，可以約束數據的保真度。同時，在算法中嵌入維納濾波器，以避免計算過程中受采樣頻率和噪聲的影響。為了求解變分問題，采用交替方向乘子進行計算，同時定義收斂準則：

(3)

k階分量可以通過下式求得：

(4)

(5)

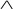
2 自適應變分模態分解算法

2.1 頻域最大值分析

當模態階次設置較少時，會導致一個模態內存在多個頻率成分，在分解過程中，需要對分解出的成分進行分析，判斷成分內是否發生模態混疊，檢驗其是否分解完全。在本方法中，選用各成分在頻域內極大值的個數和幅值大小進行判斷。引入篩選準則ξ：

(6)

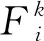
2.2 相關性分析

利用變分模態分解時，若模態階次設置過小，會造成欠分解問題，導致信號中的真實模態難以分離出來。因此，通過引入相關性分析，進一步確定模態階次。相關性系數ρ定義如下。

(7)

式中：yc為重構信號；y為原始信號；E為期望。

當相關系數較小時，欠分解問題發生，需要繼續增加模態階次。

2.3 算法流程

1)設置變分模態分解的參數，一般懲罰因子α設置為2 000。

2)設置模態階次k=1，并利用變分模態分解進行第一次分解，得到一個分量記為IMF1。

3)對IMF1進傅里葉變換，并在頻域內求出所有極值點的大小。

4)設置篩選準測ξ，當極值點間滿足該篩選準則，則認為此時模態階次k滿足要求，若不滿足該篩選準則，則增大模態階次k并重新進行變分模態分解。

5)當分解滿足篩選準則時，對分解出的k個成分進行求和并計算重構信號與原始信號的相關性，若相關性滿足閾值要求，則認為此階次較為合適，若不滿足，則繼續增大階次，重新進行變分模態分解。

3 實測數據分析

3.1 結構介紹

測試結構見圖1，為位于渤海海域的某坐底式深水網箱。該網箱容積60 000 m3，長66 m，寬66 m，最大吃水30.5 m。采用坐底式四邊形鋼結構形式，設計使用壽命10年。該網箱集成了網衣自動提升、自動投餌、水下監測、網衣清洗、成魚回收等自動化裝備，最大程度保證網箱的安全性和經濟性。除智能養殖功能外，網箱還兼具休閑旅游的功能。網箱上方建筑采用了雙層生活區模塊化建筑，有效提升了生活區利用率，周邊走臺進行加寬設計，生活區內采用高標準“中國風”裝修風格，可同時滿足30人休閑垂釣和觀光旅游需求，給客戶以舒適的度假體驗。測試時在四根立柱處分別安裝三向加速度傳感器進行測量。測試時間為260 s，采樣頻率為250 Hz。選擇其中一個傳感器的y方向測試數據進行分析，測試加速度信號的時域圖和頻域圖見圖2。

圖1 測試的深海網箱結構

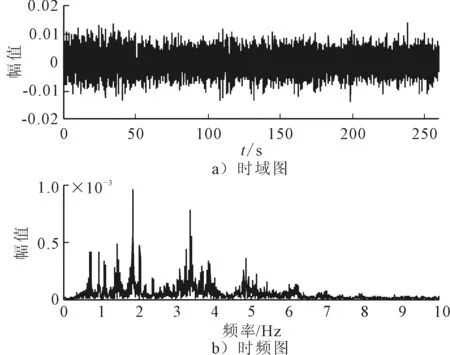
圖2 測試信號y方向的時域圖和頻域圖

3.2 分析結果

在信號分析過程中，通過使用自適應變分模態分解技術對50～90 s，共10 000個點的信號進行分解，當模態階次增加到等于86時，分解結束。對前3個成分進行展示。

由圖3可見，由改進的變分模態分解方法分解出的第一個成分對應于圖2中的一階模態，從該成分的時域圖中(圖2a))可以看到該信號較為穩定，對提取出的成分進行Hilbert變換可以得到該成分的時頻圖，見圖3b)。從時頻圖中可以看到該成分的信號頻率在1.8 Hz左右，同時在整個時間范圍內，該實測的振動信號表現出了較大的時變性。

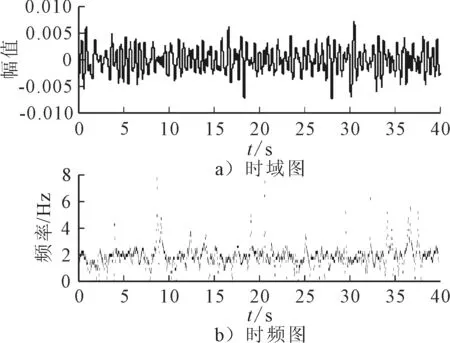
圖3 信號分解后得到的第一階模態

對分解出的第二個成分和第三個成分進行Hilbert變換，得到其時域圖和時頻圖，見圖4、5，可以看到2個成分分別對應于3.3 Hz和5.2 Hz。與圖3對比可以發現，結果與整個信號在頻域內的結果一致。在圖3中，由于頻域方法的局限性，無法展現信號頻率隨時間的變化情況，這個問題在所提出方法中也得到了解決。

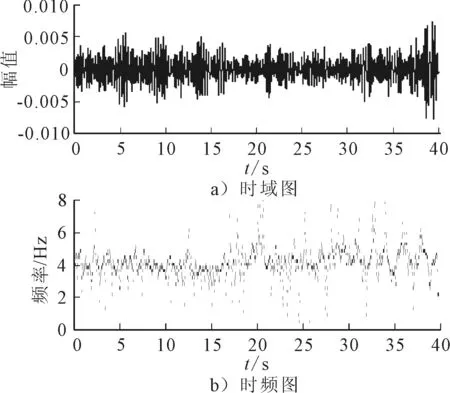
圖4 信號分解后得到的第二階模態

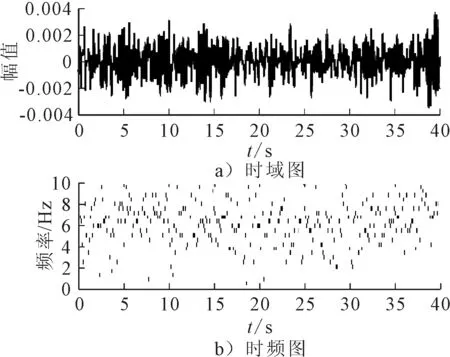
圖5 信號分解后得到的第三階模態

為了進一步驗證該方法的有效性，對分解的信號進行重構，并與原始信號進行對比，對比結果見圖6。為了使結果更加清晰，在圖6中對10～10.3 s的部分信號進行放大展示，可以看到，原始信號與重構信號吻合較好。利用式(7)計算重構信號與原始信號之間的相關性，可以得到此時相關系數為0.997 4，證明所改進的方法在處理深水網箱實測振動信號的有效性。

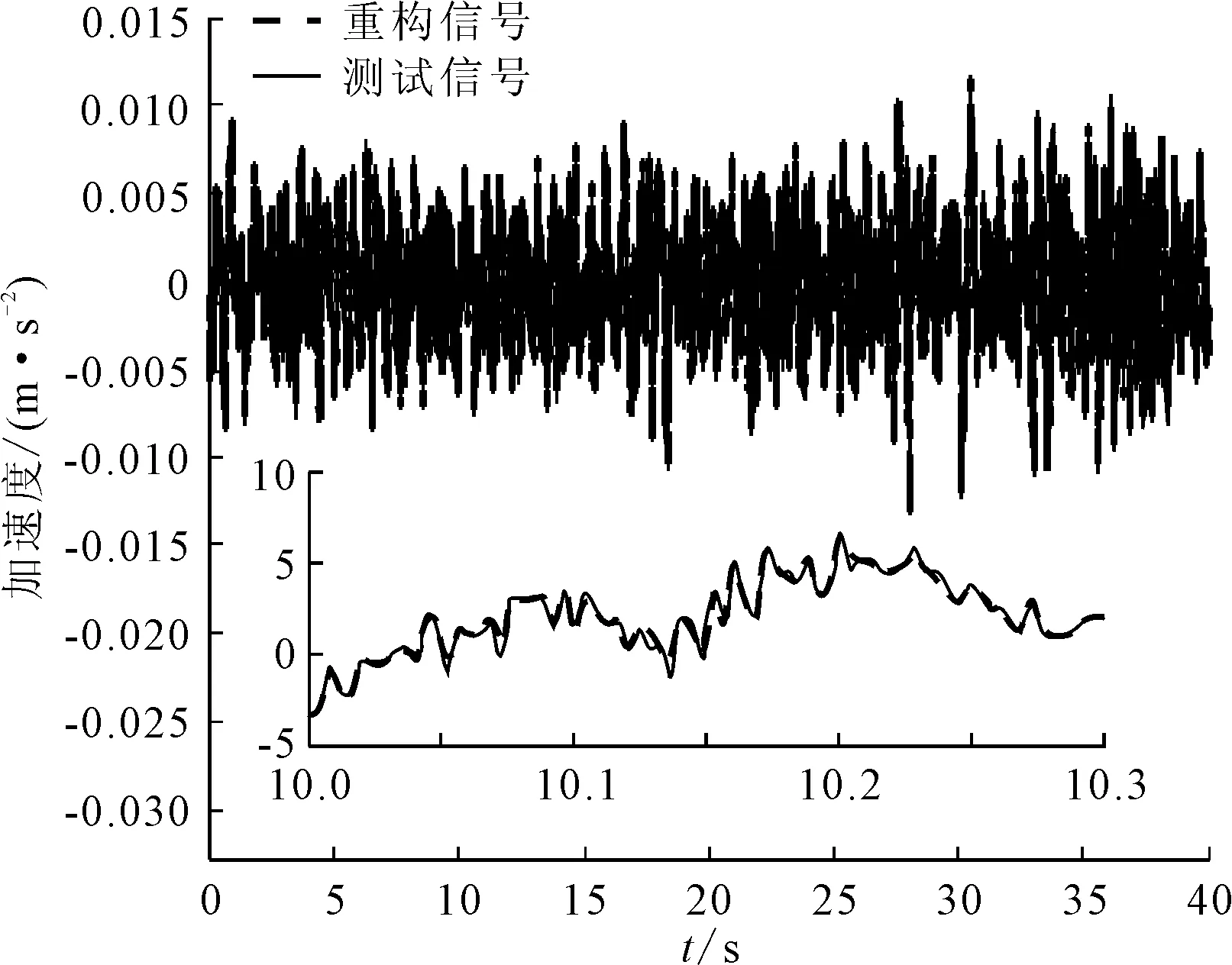
圖6 重構信號與原始信號

4 結論

在傳統變分模態分解方法中，一個主要的局限性就是其需要預先確定模態階次。本文針對這一局限性，引入了相關性分析及頻域最大值分析，提出一種自適應的變分模態分解技術。在分解過程中，由于使用了維納濾波器，使得該方法具有去噪能力。通過相關性分析和頻域最大值分析，該方法可以最小化所有固有模態函數的頻譜寬度之和，實現基于變分模態分解的信號最優分解。通過利用該方法對實測得到的深水網箱振動信號進行分解，并通過Hilbert變化可以得到分解模態的時頻圖。結果顯示，深水網箱實測信號具有較強的時變性。使用本文的方法可以對深水網箱信號進行很好地分解，也證明該方法在深水網箱結構的安全檢測中的潛在價值。

雖然改進的變分模態分解方法可以自適應的設置分解階次，其本質仍然為變分模態分解，因此，在變分模態分解中存在的其他缺陷在本文方法中仍然存在，例如端點效應，模態混疊等問題。因此，如何克服這些缺陷，使用改進方法對深水網箱的實測信號進行更為有效地分解，將作為今后的重點進行研究。