模型不確定下船舶動力定位魯棒控制器設計*

朱夢飛 徐海祥 余文曌 盧林楓

(武漢理工大學高性能船舶技術教育部重點實驗室1) 武漢 430063) (武漢理工大學交通學院2) 武漢 430063)

0 引 言

隨著海洋資源開發(fā)的深入與先進船舶技術的不斷發(fā)展，船舶動力定位控制技術廣泛應用于各類工程作業(yè)船、科學考察船和海洋平臺等，已成為深海資源開發(fā)不可或缺的關鍵支持技術，在海洋資源勘探、航行補給等領域應用甚廣[1-2].在海洋中作業(yè)的船舶會受到未知時變的環(huán)境擾動，如風、浪、流等；同時，復雜多變的海況將導致船舶模型參數產生不確定擾動.對于動力定位系統，這些不可忽略的動態(tài)未知擾動不僅會影響定位精度，還會使控制輸出不穩(wěn)定，從而導致推進器磨損以及能耗增加.

文獻[3]提出了一種環(huán)境最優(yōu)位置控制(WOPC)方法，該方法根據環(huán)境擾動的大小調整艏向角以減少能量消耗.文獻[4]針對外部擾動為已知常值和未知常值的情況，設計了魯棒無源輸出反饋控制器，實現船舶定位控制的漸近穩(wěn)定.針對在未知環(huán)境力作用下船舶橫向和艏向所受到的力和力矩具有不便測量的特點，文獻[5]提出一種基于非線性分離式原理的動力定位環(huán)境最優(yōu)控制律.文獻[6]提出了一種基于Backstepping的船舶動力定位正交神經網絡自適應控制方法，同時考慮非線性模型和未知常值環(huán)境擾動，采用正交神經網絡對數學模型的非線性項進行逼近，并采用自適應積分估計環(huán)境擾動.上述文獻大多考慮的擾動為常值，并不滿足實際情況下擾動連續(xù)非線性變化的特征.文獻[7]設計了一種滑模控制方法，基于1∶150比例的模型船實驗證實了其有效性.針對具有不確定性和未知時變擾動的水面船舶動力定位問題，文獻[8]應用矢量反步法設計了一種魯棒自適應神經控制器，采用徑向基函數(RBF)神經網絡對船舶模型動力學不確定性和時變擾動進行補償.考慮未建模環(huán)境擾動，文獻[9]提出了一種基于無源濾波的反步逆最優(yōu)控制器，利用Lyapunov函數設計了未建模擾動環(huán)境力自適應律和漸進穩(wěn)定的控制律，同時滿足了局部性能指標和全局性能指標.文獻[10]采用魯棒自適應技術和反步法設計了一種船舶艏向容錯控制器，處理外部時變環(huán)境擾動和艏向傳感器突發(fā)故障，設計參數自適應律來估計魯棒項的上界，仿真結果驗證了控制器的有效性.針對具有未知模型參數和未知時變擾動的船舶動力定位問題，文獻[11]通過將參數不確定的船舶運動數學模型和未知時變擾動分別表示為參數形式，構造處理擾動的觀測器，并利用自適應矢量反步法，設計了動力定位魯棒自適應控制律.

在分析相關文獻的基礎上，針對船舶動力定位控制問題，同時考慮船舶模型參數不確定性和未知時變環(huán)境擾動，為簡化設計過程，假設擾動上界已知，本文提出了一種船舶動力定位魯棒控制方法.基于一艘平臺供應船模型的對比仿真結果驗證了本文所提出控制律的有效性和優(yōu)越性.

1 問題的描述

1.1 船舶數學模型

對于低速運動的船舶，考慮縱蕩、橫蕩、艏搖三個自由度方向上的平面運動，根據運動學和動力學理論，船舶的非線性數學模型為

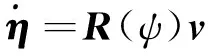
(1)

(2)

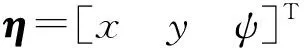
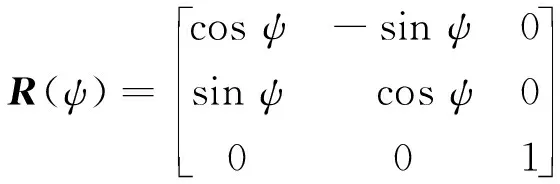
(3)

且滿足R-1(ψ)=RT(ψ)和‖R(ψ)‖=1，‖·‖表示向量或矩陣的2范數；M∈R3×3為慣性矩陣，D∈R3×3為線性阻尼矩陣，且M是正定的；b為風、浪、流等環(huán)境擾動，其未知但有界；d為船舶模型參數不確定項.

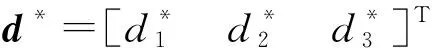
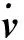
1.2 切比雪夫正交神經網絡

切比雪夫正交神經網絡廣泛應用于控制工程中，具有很強的連續(xù)非線性函數逼近能力和較快的收斂速度.其模型可以定義為

(4)

式中：wj(j=1,2,…,n)為隱藏層和輸出層之間的權重;Φj={Φ1(X),Φ2(X),…,Φn(X)}為一組切比雪夫正交多項式.

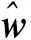
(5)

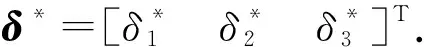
在假設1和假設2下，設計船舶魯棒自適應控制律，在存在動態(tài)擾動的情況下，使得船舶的位置收斂到期望的位置，同時保證閉環(huán)控制系統中所有的信號一致最終有界.

2 動力定位魯棒控制器設計

在假設1和假設2下，結合動態(tài)面控制技術，設計具有動態(tài)擾動的魯棒控制律，使得船舶的位置和艏向收斂到期望的位置和艏向，實現船舶的動力定位控制.控制器設計包括以下兩個步驟.

步驟1定義船舶的位置誤差向量為

z1=η-ηd

(6)

對式(6)求導可得

(7)

選取虛擬函數向量α

α=-R-1(ψ)K1z1

(8)

式中：K1為正定對稱設計矩陣.

引入狀態(tài)向量Xd，對虛擬函數向量α設計一階低通濾波器，其表示為

(9)

式中：Td為濾波器時間常數.

步驟2定義船舶的速度誤差向量為

z2=v-Xd

(10)

對式(10)求導，并乘上慣性矩陣M可得：

(11)

記神經網絡逼近誤差和模型參數不確定項所構成的復合擾動ε的界為

ε*=δ*+d*

(12)

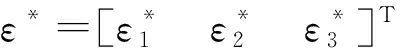
采用正交神經網絡估計時變環(huán)境擾動項RT(ψ)b，則設計的控制律為

(13)

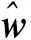
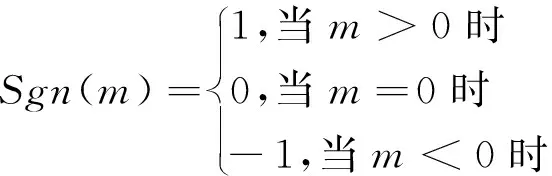
(14)

定義系統邊界層誤差向量為

z3=Xd-α

(15)

構造如下Lyapunov函數.

(16)

對其求導可得：

(17)

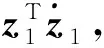
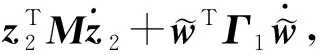
(19)

設計神經網絡權值自適應律為

(20)

式中：Γ1為待設計矩陣.

(21)

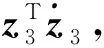
(22)

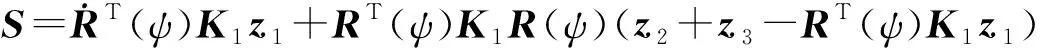
(23)

根據上述各式，可得：

(24)

式中：λmin(·)為矩陣的最小特征值，并且

(25)

(26)

λmin(K1)-β1-β2>0

(27)

(28)

(29)

根據上述分析，可得以下定理.

定理1對于具有模型參數不確定性和時變環(huán)境擾動的系統(1)和(2)，設計出具有一階低通濾波器的已知擾動界魯棒控制律，通過合理設計參數矩陣K1、K2，以及濾波器時間常數Td，能夠使得船舶的位置收斂到期望位置上，并保證該閉環(huán)系統中所有信號一致最終有界.

證明解式(24),可得

(30)

因此V(t)是一致最終有界的.根據式(16)可知，z1、z2和z3一致最終有界，那么該閉環(huán)系統中的所有信號均一致最終有界，定理1得證.

3 仿真結果與分析

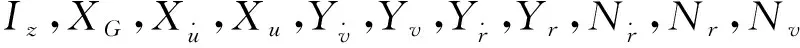
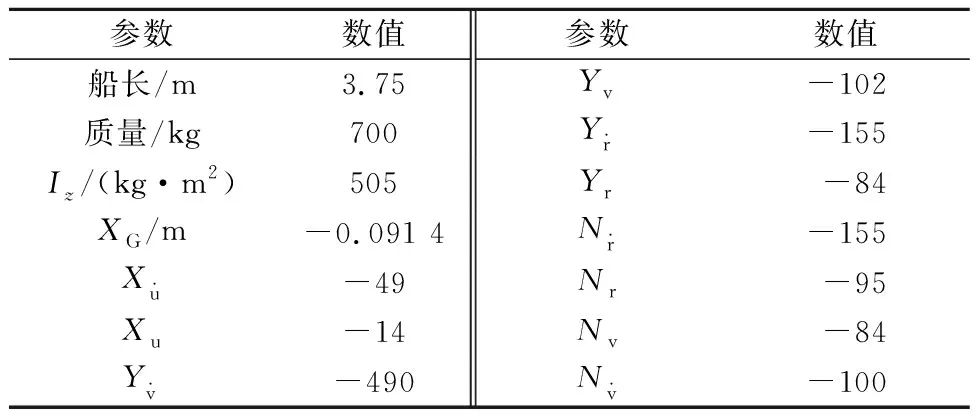
表1 船舶模型參數

本文以兩種情況對平臺供應船進行仿真研究.

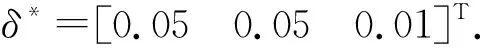
(31)

式中:Δ1為補償神經網絡逼近誤差的魯棒項；ε1=δ，表示神經網絡逼近誤差.

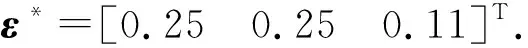
(32)

式中:Δ2為補償模型參數不確定項和神經網絡逼近誤差的魯棒項；ε2=ε.

兩種情況下的參數設置相同，相關設計參數矩陣定義為

選取的神經網絡初始權值矩陣為

并通過權值自適應律進行權值在線更新，以估計環(huán)境擾動.

仿真結果見圖1～5，其中τ1為情況1下的控制律，τ2為情況2下本文設計的魯棒控制律.北東坐標系下的船舶定位軌跡見圖1，表明τ1和τ2能夠使船舶到達期望位置并長時間保持其位置.在τ1和τ2的作用下船舶位置見圖2，τ1作用下船舶位置存在一定的誤差且艏搖角存在超調；τ2能夠使船舶準確保持在期望位置，具有較強的魯棒性.船舶速度見圖3，表明τ1和τ2作用下的u，v和r是有界的，且τ2作用下的速度更為平滑.環(huán)境擾動的估計見圖4，τ1，τ2均能夠準確地估計時變環(huán)境擾動.圖5為τ1和τ2作用下的控制輸出是合理并且有界的，且τ2作用下控制輸出更為平穩(wěn).上述結果表明，本文設計的魯棒控制律在同時存在模型參數不確定性和未知環(huán)境擾動的情況下達到了滿意的定點定位控制效果，與未考慮模型參數不確定性的情況相比，考慮了模型參數不確定性后，定位精度更高，控制輸出更平穩(wěn)合理，能夠減少推進器的磨損，從而一定程度上降低能耗.

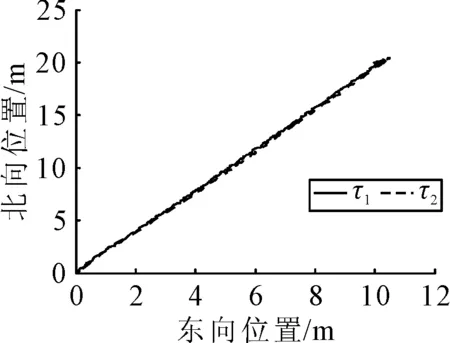
圖1 北東坐標下船舶定位軌跡

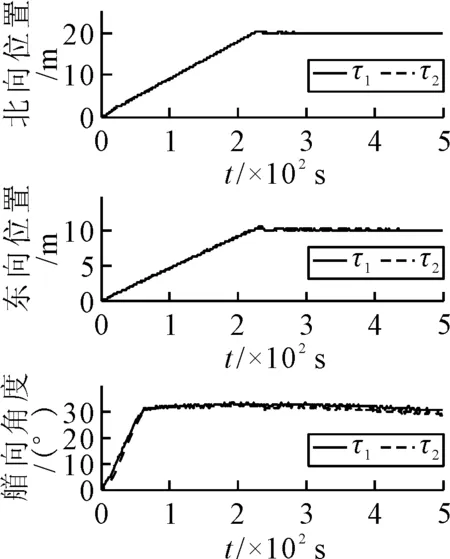
圖2 船舶位置

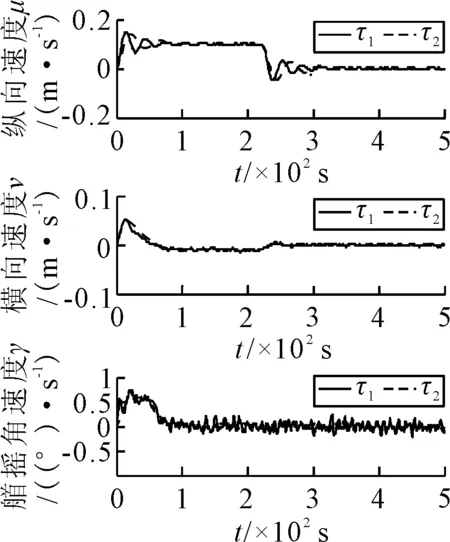
圖3 船舶速度

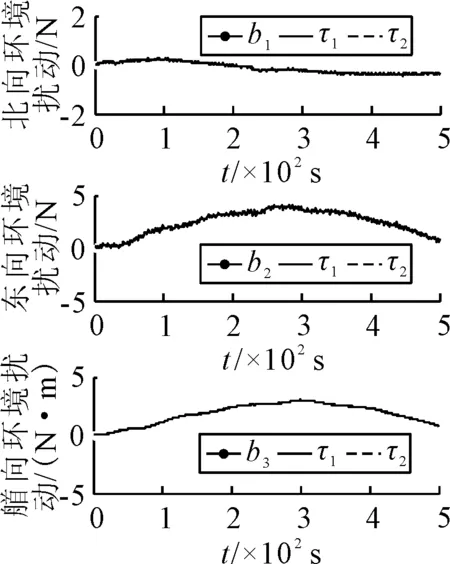
圖4 環(huán)境擾動估計

圖5 控制輸出

4 結 束 語

同時考慮模型參數不確定性和時變環(huán)境擾動，本文設計了一種船舶動力定位魯棒控制律.與動態(tài)面控制技術結合，利用一階濾波器的微分項代替虛擬控制向量的微分項，使控制律設計過程中的微分運算用簡單的代數運算代替，這樣簡化計算，易于在工程中實現.采用正交神經網絡估計環(huán)境擾動，其具有很強的連續(xù)函數逼近能力且收斂速度較快.通過設計魯棒項來補償模型參數不確定項和神經網絡逼近誤差，并假設擾動上界已知以簡化設計過程.應用Lyapunov函數證明了所設計的魯棒控制律的穩(wěn)定性，能夠使船舶位置收斂到期望位置并保證該閉環(huán)系統的所有信號一致最終有界.最后對平臺供應船模型進行了仿真，驗證了本文所提出控制律的有效性.