Scratch兩方法計算圓周率

白二娃

之前《電腦報》刊登了一篇用VB計算圓周率π值的文章。使用了π/4=1-1/3+1/5+…+1/i，計算π的近似值，i值越大精度越高。這種算法由于不夠直觀，其實不太容易理解。我另外選了兩種計算π的算法：蒙特卡羅方法和直接測量法，并用Scratch編程來計算圓周率，這樣小朋友都能很容易理解圓周率的定義和計算了。

一、 蒙特卡羅方法

蒙特卡羅方法（Monte Carlo，簡稱MC）是馮·諾依曼等人提出的統計模擬方法，蒙特卡羅這個名字來源于賭場，表示這種算法的不確定性原理與賭博類似。

假設有一個邊長為1的正方形區域，有一個圓和這個正方形內切。我們知道正方形面積是邊長a的平方，圓形面積是π乘以半徑R的平方。由于是內切圓所以正方形邊長等于2R，圓形和正方形面積的比值k等于π/4。

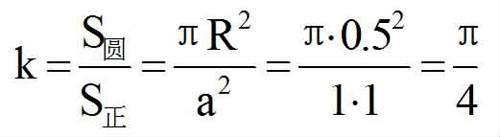
如果能夠知道k的值，就能得到π=4k，這就是估算圓周率的核心思想。

現在我們向矩形范圍內隨機畫點，任何位置被選中的概率都是相等的，圖中共投了1000個點，經過統計落在圓內的點為787個，由于投點是隨機的，所以可以近似認為圓形和矩形的面積比k等于點數比，即k=787/1000=0.787，所以圓周率π=4k=4x0.787=3.148，至此圓周率π的估算已經完成。

新建角色“圓心”和“筆”，“圓心”就在（0，0）畫一個點，“筆”隱藏顯示。

在程序中我們設置了3個變量，“pi”存儲π值、“總投放點數”設置總數、“落在范圍內的點”記錄在圓內的點。

調用畫筆擴展，重復執行“總投放點數”次。在XY坐標-90到90之間的方形區域隨機畫點。

判斷如果隨機畫的這個點到角色“圓心”的距離大于90不成立。即表示這個點在圓的范圍內（含圓的邊）。將“落在范圍內的點”加1。

循環完畢，用“落在范圍內的點”除以“總投放點數”就獲得面積比k，乘以4就得到π值了。運行時請打開加速模式，不然會運算到天荒地老。

蒙特卡羅方法是一種依賴于重復性隨機采樣，進而獲得數值解的建模方法。對于復雜曲線積分這種很難通過理論求解的情況，可以通過蒙特卡羅方法獲得一個近似解。我們用Scratch編程后多次運行就可發現，算出的π值偏差比較大，而提高“總投放點數”并不能很好地提升計算精度，這應該是由于計算機產生的隨機數是偽隨機數造成的。

二、 直接測量法

我們知道π的定義是圓的周長與直徑的比值。

我們用Scratch畫出半個邊數超多（100000條邊）的多邊形。這個多邊形由于每條邊都很短，可以認為近似是一個圓，這個半圓的終點到起點間的距離就是圓的直徑。邊長乘以邊數就是這個圓的周長。兩者相除就可以算出π的值了。

新建角色“起點”，在造型中背景放到最大后在中心點一個小點。移動到（0，-160）作為起點位置。

對小貓編程。

設置“pi”記錄計算結果，通過控制“邊長”（0.01）、“邊數”（100000）的大小控制近似圓形的大小，提高計算π值的精度，邊數越多π的精度應該越高。

移動到（0，-160）的起點位置，面向90度方向，重復執行邊數除以2次，因為我們只需要畫一個半圓用來測量直徑。畫正多邊形的方法《電腦報》以前已經介紹過就是移動“邊長”步，左轉360除以“邊數”度。這樣畫出的半圓形終點到角色“起點”之間的距離就是圓的直徑。

邊長乘以邊數就是圓的近似周長。

將“pi”設為“邊長”*“邊數”/到“起點”的距離。

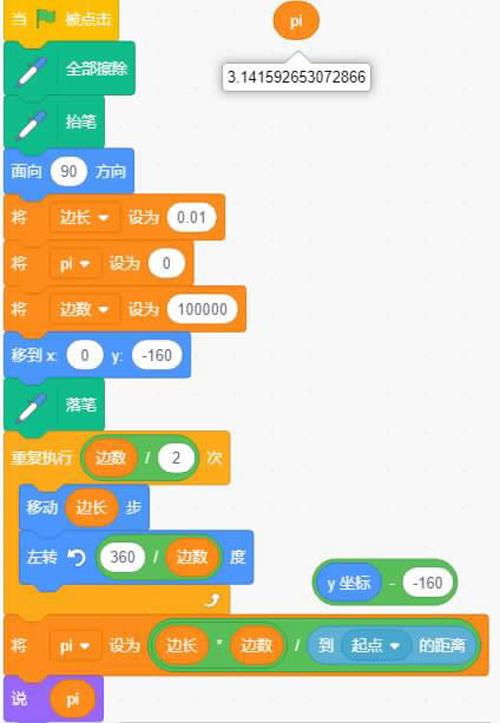
要想看到最精確的計算結果，有一個小技巧，要點擊單獨放在代碼區的變量“pi”才行。計算結果為3.141592653072866與我們已知的π值相當接近，說明這個方法計算結果相當精確。

這個方法的思維方法最為直接，就是測量出圓的周長和直徑直接相除就可以得到π值。但是對于古人來說周長和直徑都很難精確測量，所以才有那么多數學家想方設法去提高π的計算精度，但是對于程序來說這個直接的方法卻意外的容易和精確。

我們程序中設定的邊長和邊數數值只是個經驗數值，只是因為畫出來的半圓大小比較合適。其實只要多邊形邊數超過100條邊時π值的精度就已經達到3.141了，比蒙特卡羅方法效果好得多，隨著邊數的提高計算精度穩步提升，而且邊長對于π計算結果影響不大，只是影響視覺效果而已。