可持續氣象信息中心的雙極PROMETHEE動態評價方法

張皓宇 韓瑩 季正武

0 引言

我國多個行業的“十三五”規劃中，都強調了可持續發展的重要性.隨著信息特別是大數據時代的到來，各氣象信息中心的電子產品、高性能計算機等淘汰更新加快，其環境污染問題逐漸呈現出來.有鑒于此，本文首次將可持續發展概念引入到氣象信息中心的管理評價中.

PROMETHEE (Preference Ranking Organization Methods for Enrichment Evaluations)評價由所有方案對每個屬性兩兩比較得出，比較結果由偏好函數衡量.這種比較方式使得PROMETHEE方法與其他評價方法相比，能夠綜合考慮到不同評價指標間的相對重要性以及同一評價指標下的相對偏好度，具有較大優勢[1].經過多年的發展，PROMETHEE方法衍生出了多種擴展版本[2-5].其中，PROMETHEE II方法[6]相較于傳統PROMETHEE方法，能夠有效得到各評價方案的完全序而非偏序，因此本文采用PROMETHEE II評價方法.

然而，現有的PROMETHEE II方法在可持續氣象信息中心評價中存在一些缺陷：由于可持續概念的引入，經濟、環境、社會三大支柱之間的矛盾必然導致氣象信息評價中產生大量沖突信息[7-8].新近提出的雙極模糊集可以對沖突信息有效建模[9-13].因此，本文首先將PROMETHEE II方法推廣到雙極模糊環境.可持續發展顯然是一個多年的動態變化過程，而現有的PROMETHEE II方法中都是靜態的.因此，本文在PROMETHEE II方法中引入時間動態因子，從而實現對可持續氣象信息中心的動態評價,實例分析表明了本文提出的新算法的有效性.

綜上，本文給出了一種新的可持續氣象信息中心的雙極PROMETHEE動態評價方法.主要創新點如下：

1)首次將可持續發展概念和雙極模糊理論引入到氣象信息中心評價管理中，充分考慮了對可持續氣象信息中心評價可能影響中的不確定性、沖突性；

2)將靜態PROMETHEE方法推廣到了雙極模糊環境，并引入時間因子，利用非線性規劃模型確定時間權重，從而可以實現對可持續氣象信息中心的動態評價.

1 預備知識

本章主要回顧一些基本知識.

現實問題的處理中，數據的沖突和不相容越來越普遍，雙極模糊集在實際應用中顯然更符合決策者的需要.下面給出雙極模糊集的一些相關概念以及運算法則[9].

設U為有限論域，任意的u∈U，定義BP:U→[0,1],BN:U→[-1,0]，則稱B=(BP(u),BN(u))為論域U上的雙極模糊集.正隸屬度BP(u)表示元素u關于雙極模糊集B對某性質的滿足程度，而負隸屬度BN(u)則表示對該性質相反性質的滿足程度.

設在有限論域U上，任意的u∈U，有兩個雙極模糊集A=(AP(u),AN(u))和B=(BP(u),BN(u))，若A≤B，則AP(u)≤BP(u)且AN(u)≥BN(u).

PROMETHEE方法中一個中心環節就是偏好函數的構建，為了使偏好函數能夠更好地量化決策者的偏好差異.本文采用了無差別區間的線性關系偏好函數[14].設某評價問題的評價指標集為C={c1,c2,…,cn}，指標相關的無差別區間的線性關系偏好函數定義如下：

(1)

其中，dj(a,b)=fj(a)-fj(b)，表示方案a，b評價指標cj處的數值之差.p取dmax表示方案a,b在不同指標下所能取得的最大數值之差;對應q=dmin表示方案a,b在不同指標下所能取得的最小數值之差.

2 模型與方法

本章將PROMETHEE II 方法推廣到雙極，并引入時間因子，給出一種充分考慮氣象信息中心可持續評價中沖突、不確定、動態變化等特性的雙極PROMETHEE動態評價方法.

步驟1:構建初始的雙極模糊氣象信息中心可持續評價矩陣.

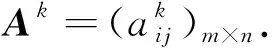
步驟2:利用非線性規劃模型確定時間權重.

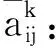
(2)

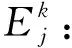
(3)

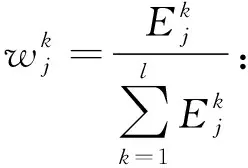
當方案集在屬性cj下的評價值在某個時刻tk離散程度較大時，那么tk時刻所對應的時間權重就越大，其對決策結果的影響也就越大.

步驟3：由式(4)加權求得氣象信息中心可持續發展綜合雙極模糊評價矩陣A=(aij)m×n：

(4)

步驟4：對綜合雙極模糊評價矩陣A利用熵權法計算得到指標權重向量.

步驟5：利用式(5)、(6)分別計算總體偏好指數H(ui,uj)和H(uj,ui):

(5)

(6)

其中，Pj(ui,uj)是由式(1)計算得到的.

步驟6：利用式(7)、(8)分別計算方案ui的流入量φ+(ui)與流出量φ-(ui):

(7)

(8)

步驟7：利用式(9)計算凈流量φ(ui)，并對所有氣象信息中心進行優劣排序:

φ(ui)=φ+(ui)-φ+(ui).

(9)

根據各氣象信息中心的凈流量對方案集進行排序，凈流量數值越高，對應氣象信息中心的可持續發展能力越強.

3 實例驗證

本章將通過一個實例，驗證新提出的算法的有效性.

步驟1：構建初始的雙極模糊氣象信息中心可持續評價矩陣.

對4個氣象信息中心u1，u2，u3，u4的可持續發展能力進行評價.評價指標為：c1，對地方經濟產業支持力;c2，綠色供應商選擇;c3，創新能力;c4，設備儀器先進程度;c5，碳減排能力;c6，環保改善成本投入.全部為效益型指標.邀請專家對每個氣象信息中心連續4年的可持續發展能力分別進行評價，得到初始雙極模糊評價矩陣如表1—4所示.

表1 第一年雙極模糊評價矩陣Table 1 First year bipolar fuzzy evaluation matrix

表2 第二年雙極模糊評價矩陣Table 2 Second year bipolar fuzzy evaluation matrix

表3 第三年雙極模糊評價矩陣Table 3 Third year bipolar fuzzy evaluation matrix

表4 第四年雙極模糊評價矩陣Table 4 Fourth year bipolar fuzzy evaluation matrix

步驟2：利用非線性規劃模型確定時間權重，得到時間權重矩陣W:

步驟3：由式(4)加權求得氣象信息中心可持續發展綜合雙極模糊評價矩陣A，如表5所示.

表5 綜合雙極模糊評價矩陣Table 5 Comprehensive bipolar fuzzy evaluation matrix

步驟4：對綜合雙極模糊評價矩陣A利用熵權法計算得到指標權重向量：

?=(0.174 5,0.165 5,0.165 1,0.164 6,0.164 5,

0.165 8).

步驟5：利用式(5)、(6)分別計算總體偏好指數H(ui,uj)和H(uj,ui)，如表6所示.

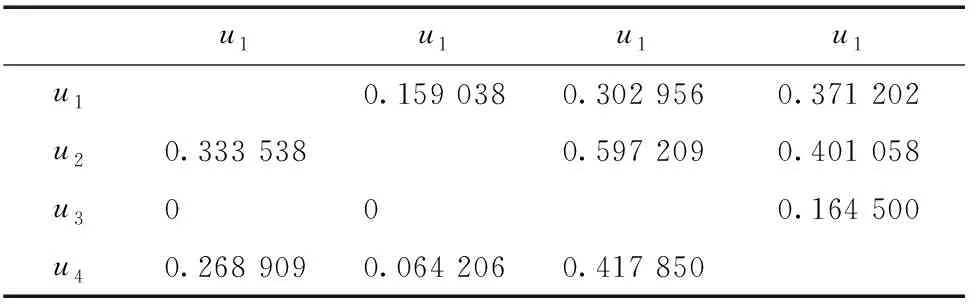
表6 待評價氣象信息中心的總體偏好函數Table 6 General preference function of meteorological information center to be evaluated

步驟6：利用式(7)、(8)分別計算方案ui的流入量φ+(ui)與流出量φ-(ui)，如表7所示.

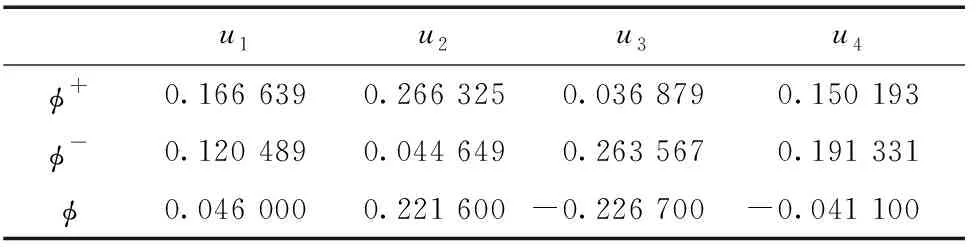
表7 待評價氣象信息中心的流出量、流入量與凈流入量Table 7 Outflow,inflow and net inflow of meteorological information center to be evaluated

步驟7：利用式(9)計算凈流量φ(ui)，并對所有氣象信息中心進行優劣排序.

氣象信息中心可持續發展能力排序為：u2>u1>u4>u3.

4 對比分析

不考慮指標中的兩極性與沖突性，僅使用雙極模糊評價值中的正極數據求解，忽視負極數據，將雙極模糊評價矩陣轉化為普通的模糊評價矩陣，利用單極PROMETHEE II方法，時間權重沿用本例中數據，最終得到的凈流量為(-0.029 4,0.117 6,-0.052,-0.036 1).為了方便對比前后凈流量的變化，將雙極值模糊環境下的凈流量φ1，及傳統模糊集環境下的凈流量φ2繪成折線圖進行對比，如圖1所示.

根據氣象信息中心凈流量排序可知，在只考慮單極的情況下的模糊PROMETHEE II方法中，氣象信息中心可持續發展能力排序為：u2>u1>u3>u4.與原有結果不同的是，在只考慮單極數據的情況下，氣象信息中心u3的可持續發展能力要優于氣象信息中心u4.這是因為只考慮雙極正極評價值的時候忽略了氣象信息中心可持續化發展指標中存在的不相容性與兩極性.

觀察案例中的備選氣象信息中心u3和u4，當只考慮正面影響的時候，氣象信息中心u3顯然是優于u4的.但是，我們同時將指標中的負面效應也考慮進來，氣象信息中心u4的評價就明顯優于氣象信息中心u3.原因在于氣象信息中心u4在負極數據上的評價要遠優于氣象信息中心u3.

5 結束語

本文在雙極模糊集的理論基礎上，引入時間權重的概念，將在雙極模糊集環境下的氣象信息中心可持續發展能力評價研究由靜態推廣到了動態，并結合PROMETHEE II排序方法對氣象信息中心可持續發展水平進行綜合評價.新方法不僅利用雙極模糊集的特性，考慮了氣象信息中心可持續發展評價中屬性的兩極性與不相容性，還注意到了時間權重對評價結果的影響.通過具體的實例驗證及結果分析，驗證了建立的可持續氣象信息中心發展能力動態評價模型的可行性和合理性.在后續工作中，將研究如何從網絡爬取有效數據，并引入深度學習方法進行研究.