基于積分器初值的無人機飛行控制律平滑切換方法
郝現偉,李皓偉,李 鐸
(北京宇航系統工程研究所,北京 100076)
0 引言
運載火箭、無人機等飛行器飛行控制系統不僅要完成軌跡制導與姿態控制,還要完成導航和飛行任務管理,是關系飛行器飛行成敗的關鍵系統之一,因此為保證飛行器圓滿完成飛行任務,須確保飛行控制系統具有很高的可靠性和安全性[1-2]。
無人機自主飛行過程包括起飛、爬升、定高、下降、下滑、拉平、著陸滑跑等飛行階段,每個飛行階段具有不同的控制目標[3]。為保證無人機在每個飛行階段均具有較好的控制性能,需根據無人機特性及各飛行階段的控制目標,設計相應的飛行控制律。不同的飛行階段可能采用不同的控制律,這必然面臨著多組復雜控制律之間的切換問題。控制律之間的切換可能會引起舵面瞬間跳變,從而產生較大的力矩,姿態變化劇烈,可能使無人機不可控,因此如何實現多組復雜控制律之間的平滑切換,避免舵面瞬變,是無人機自主飛行控制的關鍵技術。
對于多模態控制律切換問題,段廣仁等[4]基于參數化特征結構配置結果及模型跟蹤方法,設計了滿足輸出跟蹤性能并使多模型系統中各閉環子系統逐漸穩定的多模型切換控制律集合,通過協調選取各子系統控制律中的參數來抑制切換時刻的輸出跳變,這種方法理論性太強,工程可實現性較差;王元超等[5]基于Stateflow給出了6種飛行模態之間的控制律邏輯切換條件,但沒有對不同飛行模態之間控制律平滑切換進行研究。目前,工程上常采用的控制律平滑切換方法有雙模態同步運算瞬變抑制法和單模態運算瞬變抑制法[6]。雖然雙模態同步運算瞬變抑制法瞬變抑制效果明顯,但需要同時運算兩種模態的飛行控制律,將占用過多的計算機機時和內存,并且在切換過程中系統的穩定裕度難以確定。單模態運算瞬變抑制法在雙模態同步運算瞬變抑制法的基礎上做了改進,雖然只須運算當前模態的飛行控制律,克服了雙模態抑制法須同時運算兩組控制律的缺點,但是切換過程中系統的穩定裕度仍難以確定,并且要根據經驗調整淡入淡出時間參數,以達到較好的切換效果。
針對無人機多組復雜控制律之間的平滑切換問題,本文提出基于積分器初值的控制律平滑切換方法。首先將復雜控制律的各個環節進行形式變換,拆分成由比例和積分組成的基本單元結構;然后以舵面平滑切換為目標,由后向前(從舵面指令向給定指令方向)依次遞推出復雜控制律中所有積分器的初值,從而實現不同控制律之間的平滑切換。通過算例仿真驗證不同控制律之間平滑切換方法的有效性。
1 問題描述
無人機各飛行階段控制目標不同,控制率也不同,因此需進行多組控制率切換。若多組控制率切換問題處理不當,會引起舵面跳變,可能造成無人機飛行姿態劇烈變化,致使無人機不可控。尤其在進場著陸階段,無人機會經歷下滑、拉平和著陸滑跑,該過程無人機飛行高度和飛行速度逐漸降低,對無人機的接地速度、接地俯仰角、側偏距等均有較強的約束性[7],此時采取措施抑制舵面瞬變實現復雜控制律之間的平滑切換,可提高無人機對期望著陸軌跡的跟蹤精度,提高無人機的著陸平穩性和安全性。
復雜控制律之間的切換示意圖如圖1所示。圖1中,飛行模態1對應著控制律A,飛行模態2對應著控制律B。控制律A和B為常規的PID控制,由PID控制器和綜合校正環節組成。在控制律切換之前,無人機處于飛行模態1,通過運算控制律A得到舵面偏角指令δc=δc1。當滿足控制律切換條件后,無人機轉為飛行模態2,此時任務管理與控制律調度模塊發出指令由控制律A切換成適用于飛行模態2的控制律B,通過運算控制律B得到舵面偏角指令δc=δc2。由此可見,如何保證控制律切換后的第一個運算周期,使經控制律B解算得到的δc2等于前一個運算周期經控制律A解算得到的δc1,是實現兩組控制律之間平滑切換的關鍵研究。
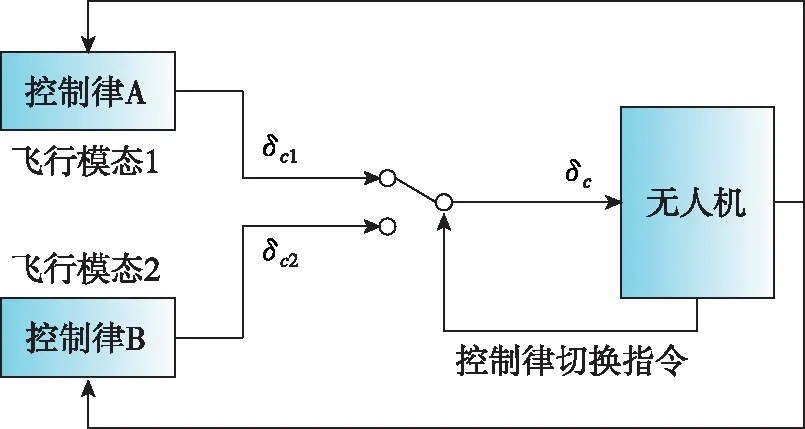
圖1 復雜控制律之間的切換示意圖Fig.1 Smooth switching between complex control laws
2 飛行控制律平滑切換方法
無人飛行控制律通常為常規PID控制,包括PID控制器和綜合校正環節。由數字積分器工作原理[8]可知,在控制律切換后的第一個運算周期,積分器輸出值為初值,在之后的運算周期,積分器輸出值為初值累加積分器輸入值。根據此積分器的特性,在控制律切換后的第一個運算周期,首先將復雜控制律的各個環節進行形式變換,拆分成由比例和積分組成的基本單元結構,然后以舵面平滑切換為目標,由后向前(從舵面指令向給定指令方向)依次遞推出復雜控制律中所有積分器的初值,之后再對復雜控制律中所有積分器賦上遞推出的初值,即可使經新控制律解算得到的舵偏指令與經前控制律切換前最后一個運算周期解算得到的舵偏指令相等,最終實現兩組控制律之間平滑切換。
(1)
拆分后的校正環節Gjz(s)的結構如圖2所示。
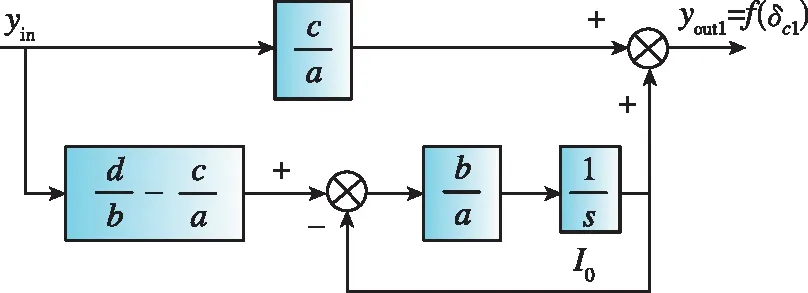
圖2 校正環節拆分后的結構圖Fig.2 Diagram of the correction link after split
圖2中含有積分器環節。定義yin為校正環節輸入值,yout為校正環節輸出值,I0為積分器初值。
控制律切換時,以下等式成立
(2)
可推導出積分器初值I0和校正環節輸入值yin的表達式
(3)
式中,輸出值yout與前一個運行周期的舵面偏角指令有關,即yout=f(δc1)。
PID控制器結構如圖3所示。
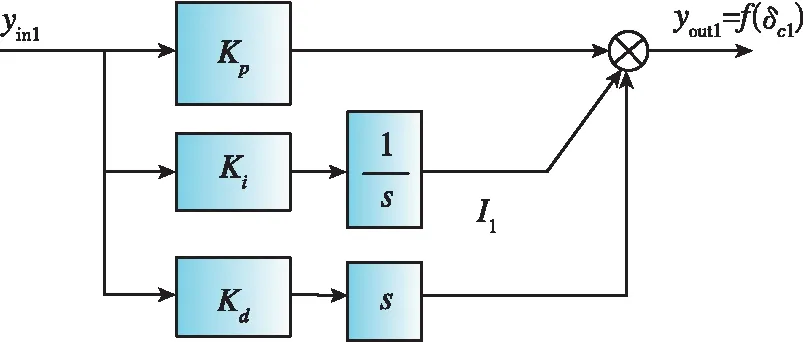
圖3 PID控制器結構圖Fig.3 PID controller structure
控制律切換時,以下等式成立
(4)
可推導出積分器初值I1的表達式
(5)
式中,輸出值yout1與前一個運行周期的舵面偏角指令有關,即yout1=f(δc1)。
控制律切換時刻,已知前一個運行周期舵面偏角指令δc1,則可求得yout,yout1的值,進而根據式(3),(5)可求得積分器初值I0,I1。
將推導出的積分器初值賦入新控制律中相應的積分器中,在控制律切換后的第一個運算周期經新控制律解算的舵面偏轉指令即可與前一個運行周期的舵面偏角指令相等,從而實現不同控制律之間的平滑切換。
3 算例
以某無人機進場著陸為例,對兩種飛行模態下升降舵通道不同控制律之間的切換進行分析。
某無人機進場著陸飛行,為增升需要,襟翼將下偏至某規定位置,同時當滿足起落架釋放條件后,無人機起落架將緩慢放下,該過程稱為構型變化。為保證構型變化前后的俯仰通道著陸控制系統均具有較好的控制性能,設計了兩組不同的飛行控制律,則必然面臨著兩組控制律之間的切換問題。控制律之間的切換可能會引起升降舵舵面瞬間跳變,從而產生較大的俯仰力矩,致使飛行器姿態劇烈變化,因此需采用抑制措施,避免舵面瞬變。圖4給出了構型變化后的升降舵通道控制結構。

圖4 構型變化后的升降舵通道控制結構Fig.4 Control structure of the pitch channel after the configuration change
圖4中,PID控制器結構如圖3所示,控制律參數包括Kp,Ki,Kd。各控制律參數值如下
Kp=1.5,Ki=0.32,Kd=0.9,K?=2.3,Kωz=1.2,a=1,b=3.11,c=2.16,d=2.31,a1=1,b1=4.84,c1=0.77,d1=2.57
根據第2節提出的基于積分器初值的控制律平滑切換方法,對圖4中兩個校正環節和PID環節共3個積分器賦初值。用Ih0表示內回路校正環節中積分器的初值,用Ih1表示外回路校正環節中積分器的初值,用Ih2表示外回路PID環節中積分器的初值,已知控制律切換時刻前一個運行周期的舵面偏角指令為δe1,則Ih0,Ih1,Ih2的表達式為
(6)
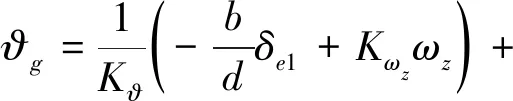
為檢驗本文提出的基于積分器初值的控制律平滑切換方法的合理性和有效性,以下分別采用雙模態同步運算瞬變抑制法、單模態運算瞬變抑制法和積分器賦初值法進行非線性全量仿真對比。記錄并給出飛行高度、高度差(正高度差表示期望高度大于實際飛行高度)、升降舵指令、法向過載和俯仰角的響應曲線,如圖5所示,圖中xd為無人機距理想接地點的水平距離。
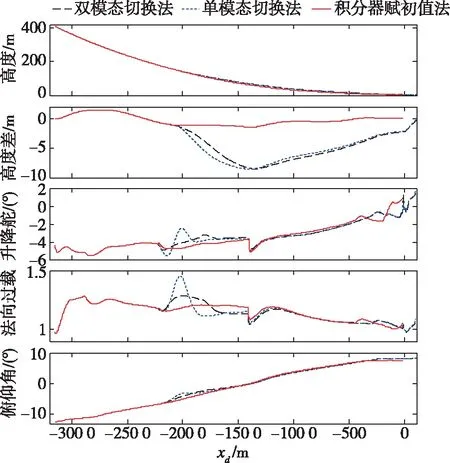
圖5 復雜控制律平滑切換仿真對比Fig.5 Simulation comparison of complex control law smooth switching
由圖5可見,采用雙模態切換法和單模態切換法時,飛行器對期望著陸軌跡的跟蹤精度較差(最大高度跟蹤誤差均近9 m),著陸飛行過程波動較大(最大法向過載分別為1.32和1.46),接地散布較大(實際接地點距理想接地點的縱向偏差為98 m);但采用本文提出的串聯遞推積分器初值控制律平滑切換方法時,無人機對期望著陸軌跡的跟蹤精度最高(最大高度跟蹤誤差為1.3 m),實際接地點距理想接地點的縱向偏差最小(僅為-16.3 m),接地散布最小,著陸飛行過程最平穩(最大法向過載為1.18)。由此可見,本文提出的控制律平滑切換方法是有效的,該方法同時提高了飛行器的著陸平穩性和安全性。
4 結論
對于無人機自主飛行過程中復雜控制律之間切換時出現的舵面瞬變問題,本文提出了基于積分器初值的控制律平滑切換方法,實現了復雜控制律之間的平滑切換,提高了無人機飛行平穩性和安全性。本文提出的控制律平滑切換方法不僅適用于無人機飛行控制系統,還適用于運載火箭、機器人等研究對象的控制系統,具有較高的工程應用價值。

