一類具有Michaelis-Menten型抑制項的腫瘤-免疫模型動力學分析

張改梅, 王曉琴, 李建全

(陜西科技大學文理學院，西安 710021)

癌癥已成為嚴重危害人類健康的重大公共衛(wèi)生問題。近期世界衛(wèi)生組織發(fā)表了最新的全球癌癥統(tǒng)計數據，2018年全球約有1.81×107例新的癌癥病例和9.6×106例癌癥死亡病例。由于人口的增長和人口老齡化，全球癌癥發(fā)病率和死亡率快速增長[1-2]。研究表明免疫系統(tǒng)能夠識別和消除惡性腫瘤[3-5]，數學模型模擬腫瘤免疫動力學不僅有助于理解免疫細胞和腫瘤細胞是如何相互作用的，而且也能提供一個有用的工具來預測免疫治療的結果和改善治療策略。

作為腫瘤免疫效應階段的執(zhí)行場所，腫瘤微環(huán)境內存在許多因素參與腫瘤組織與免疫系統(tǒng)的相互作用。由于腫瘤微環(huán)境的復雜性，不僅要考慮腫瘤細胞和效應細胞自身的增殖和死亡、免疫效應細胞對腫瘤細胞的抑制作用，也需要考慮腫瘤對效應細胞的作用。腫瘤的出現(xiàn)會刺激效應細胞的增長，同時，腫瘤對效應細胞也有抑制作用，如腫瘤可通過降低微環(huán)境中葡萄糖的濃度來抑制免疫效應細胞的活性；腫瘤微環(huán)境常呈現(xiàn)酸性，在酸性條件下，免疫效應細胞的活性明顯降低，而且腫瘤細胞本身也參與腫瘤微環(huán)境中的免疫抑制[6]。

關于腫瘤免疫相互作用的模型已有許多學者研究[7-10]。1994年，Kuznetsov等[11]提出了二維腫瘤免疫反應的數學模型:

(1)

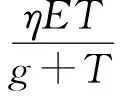
Delisi等[12]、Adam[13]研究了腫瘤細胞與效應細胞相互作用的常微分方程模型，這兩個模型均采用Michaelis-Menten型抑制函數來表示效應細胞對腫瘤細胞的抑制作用。研究結果均顯示一定范圍內，效應細胞的增長會增大腫瘤細胞的存活率。此外，他們還給出了腫瘤生長不受免疫系統(tǒng)控制變?yōu)閻盒阅[瘤的閾值條件。Kirschner等[14]在文獻[11-12]的基礎上，假設腫瘤對效應細胞的刺激項為線性項，首次提出了腫瘤細胞、免疫效應細胞和IL-2之間的相互作用的數學模型。研究發(fā)現(xiàn)腫瘤的抗原性對該模型的動力學性質有著非常大的影響，并解釋了腫瘤復發(fā)的原因。2015年，Yang等[15]在文獻[14]基礎上加入了脈沖免疫治療，建立了一個與腫瘤-免疫及脈沖免疫治療相關的數學模型，研究發(fā)現(xiàn)效應細胞的初始密度、效應細胞與腫瘤細胞的比例、免疫治療周期等對癌癥的治療至關重要[15]。Parthasakha等[16]提出了具有Monod-Haldane動力學反應的腫瘤免疫與IL-2之間相互作用的時滯數學模型，以揭示相關細胞間現(xiàn)象的動力學機制。確定了模型解的正性、有界性和一致持久性，發(fā)現(xiàn)模型在無腫瘤平衡態(tài)下存在跨臨界分支。Duan等[17]對高斯白噪聲驅動的腫瘤免疫系統(tǒng)的穩(wěn)定性進行了研究。研究發(fā)現(xiàn)在這個系統(tǒng)中，有幾個穩(wěn)態(tài)。當且僅當噪聲較弱時，一個穩(wěn)態(tài)是全局漸近穩(wěn)定的，而當噪聲較強或較弱時，另一個穩(wěn)態(tài)總是不穩(wěn)定的。Li等[18]提出并研究了隨機切換環(huán)境下腫瘤細胞與免疫系統(tǒng)之間的競爭模型。得到了腫瘤細胞滅絕和持續(xù)存在的理論閾值。此外，還進行了隨機模擬來證實和解釋這些結論。

由于目前尚未有模型用Michaelis-Menten形式來表示腫瘤對效應細胞的抑制作用，因此在假設腫瘤細胞對免疫效應細胞具有線性刺激率和Michaelis-Menten型抑制函數的基礎上，建立了如式(2)所示的腫瘤細胞與效應細胞相互作用的動力學模型:

(2)

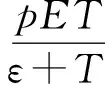
分析了式(2)平衡點的存在性、局部漸近穩(wěn)定性和全局動力學行為，以及模型產生鞍結點分支的條件，并進一步考慮腫瘤細胞對效應細胞的抑制率系數和效應細胞對腫瘤細胞的抑制率系數對式(2)動力學行為的影響。最后對所得結果進行生物學意義的解釋和數值模擬來驗證所得結果。

1 解的非負性和有界性

關于式(2)解的非負性和有界性有如下結論。

定理1設E(t)、T(t)為式(2)滿足非負初始條件的解, 則E(t)、T(t)是非負的且最終有界。

證明首先，易知T=0為式(2)第二個方程的解，根據解的存在唯一性可知，在非負初始條件下T(t)≥0成立。當E(0)=0時，E′(0)>0，所以存在時刻t1，當t∈(0,t1)時，有E(t)>0；當E(0)>0時，假設存在t2>0使得E(t2)=0且當t∈(0,t2)時，有E(t)>0，所以E′(t2)≤0。而由式(2)的第一個式子可得E′(t2)=s+cT(t2)>0，這與E′(t2)≤0矛盾，所以，式(2)在非負初始條件下的解保持非負性。

其次，由式(2)的第二個方程得：

(3)

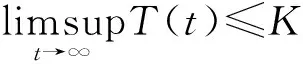
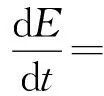
s+c(K+ε1)-μE

(4)

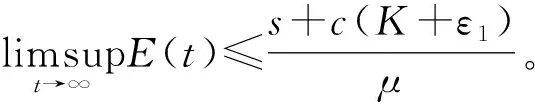
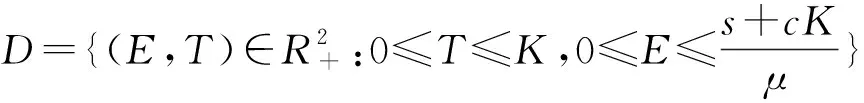
2 模型分析

2.1 平衡點的存在性

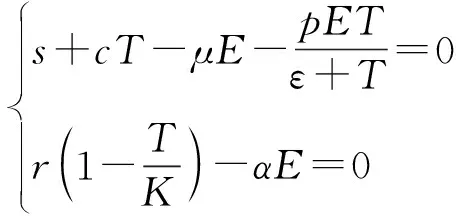
(5)

(6)

由式(6)的第二個方程可以得到：

(7)

當T≠K時，將式(7)代入式(6)的第一個方程得：

(8)

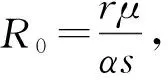
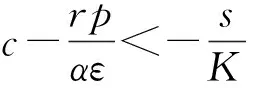
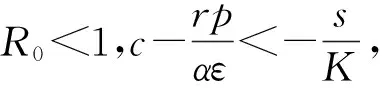
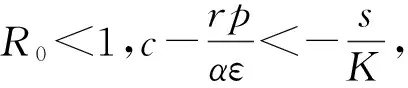
證明由于式(2)有正不變集D，所以可通過判定方程H(T)=0在區(qū)間(0,K)上根的存在性來確定的式(2)平衡點的存在性。直接計算可得:

(9)

式(9)中：H′(T)為H(T)關于T求一階導數；H″(T)為H(T)關于T求二階導數。

由于式(2)中各參數都為正數，所以在區(qū)間(0,K)內有H″(T)>0，即函數H(T)在區(qū)間(0,K)的圖形是上凹的。

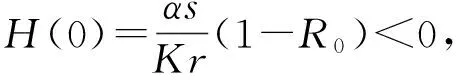
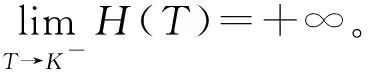
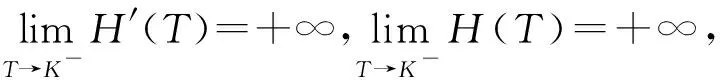
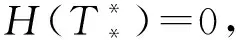
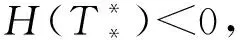
當方程H(T)=0在區(qū)間(0,K)內存在一個單根即T*時，其滿足H′(T*)>0。

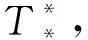
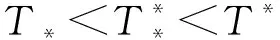
2.2 式(2)平衡點的局部穩(wěn)定性

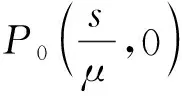
(10)

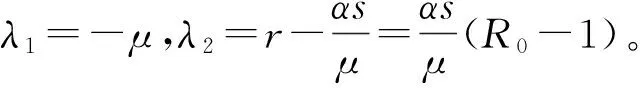
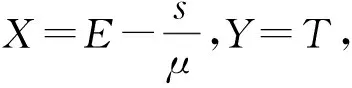
(11)

利用變換：

(12)

將式(11)化為

(13)

式(13)中：l=cαε-pr-pμ。

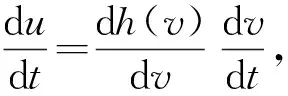
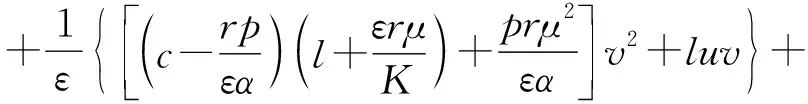
(14)

將u=av2+o(v2)代入式(14)，并比較兩端同次冪系數可得:

(15)

此時:

(16)

進一步，將式(16)代入式(13)的第二個方程中，得到中心流形上的解滿足：

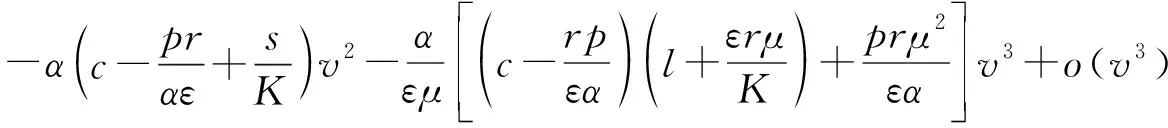
(17)

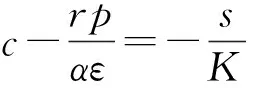
綜上所述，對式(2)邊界平衡點的局部穩(wěn)定性有如下結論。

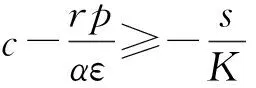
(18)

因此

(19)

由式(6)的第一個方程可得：

(20)

因此：

(21)

進一步，由式(7)可得：

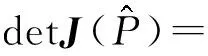
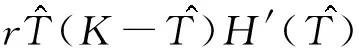
(22)

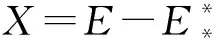
(23)

式(23)在原點附近可表示為

(24)

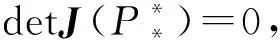
(25)

于是式(24)可寫為

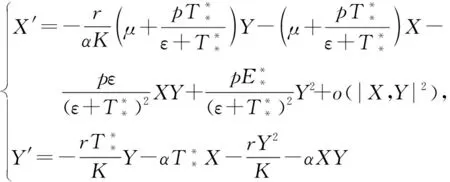
(26)

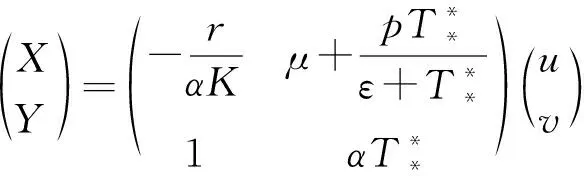
(27)

根據中心流形定理[19]，求得式(27)在原點的局部中心流形為

(28)

進一步，將式(28)代入式(27)的第一個方程，可得：

(29)

綜上所述，對式(2)正平衡點的局部穩(wěn)定性有如下結論。

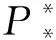
2.3 式(2)平衡點的全局分析

對式(2)，記：

(30)

(31)

因此式(2)在區(qū)域D內無閉軌線。根據式(2)平衡點的局部穩(wěn)定性，對于式(2)平衡點的全局穩(wěn)定性有如下定理。

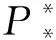
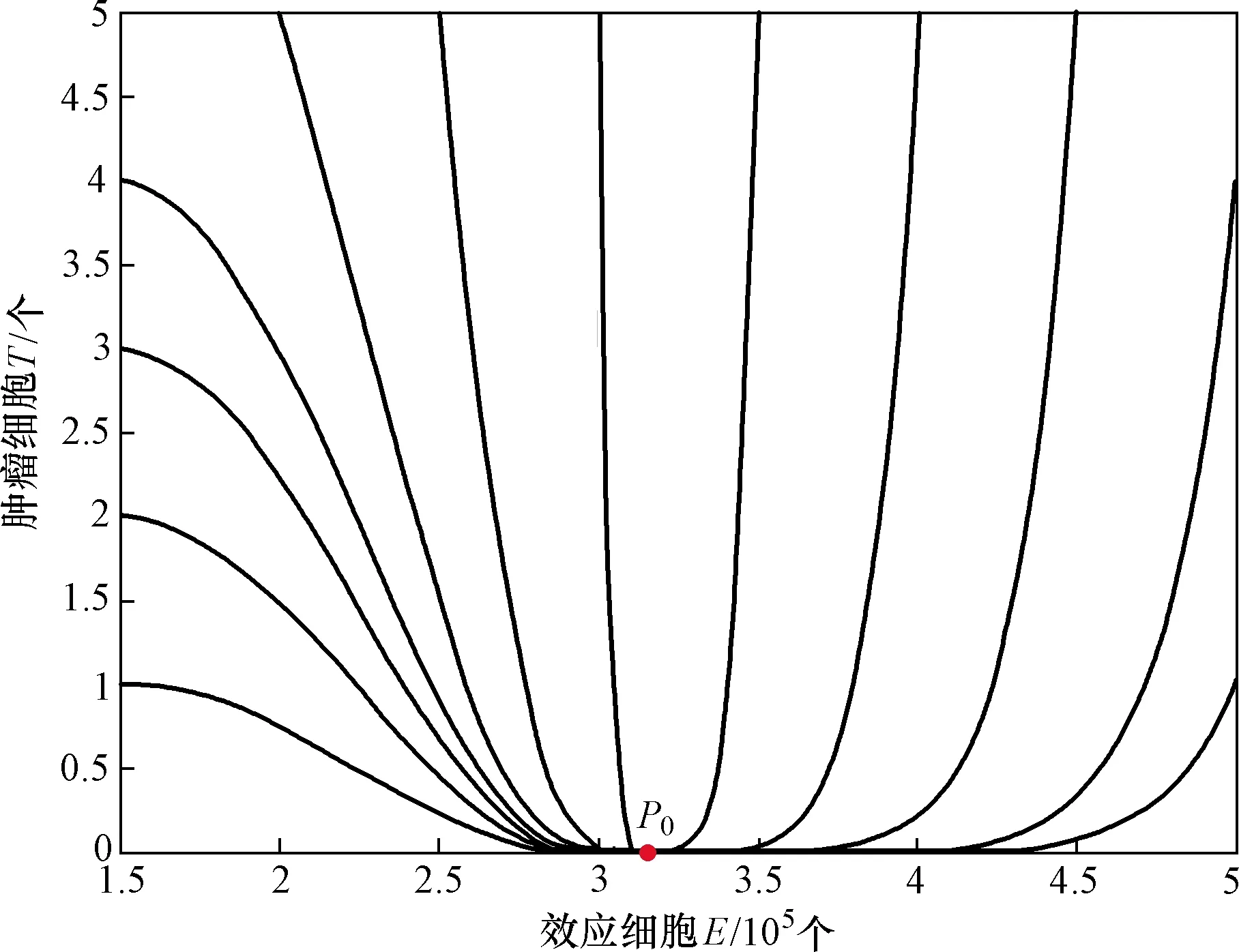
P0為無腫瘤平衡點圖1 式(2)不存在正平衡點時的情形Fig.1 The case of formula (2) without the positive equilibrium

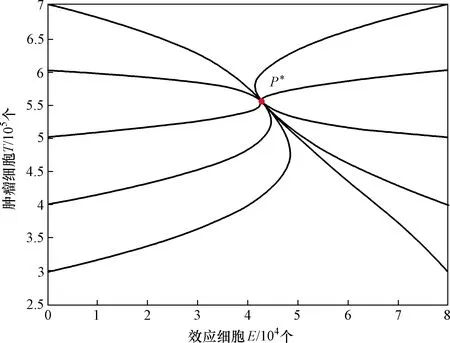
P*為模型的唯一有瘤平衡點圖2 式(2)存在唯一正平衡點時的情形Fig.2 The case of formula (2) with unique positive equilibrium

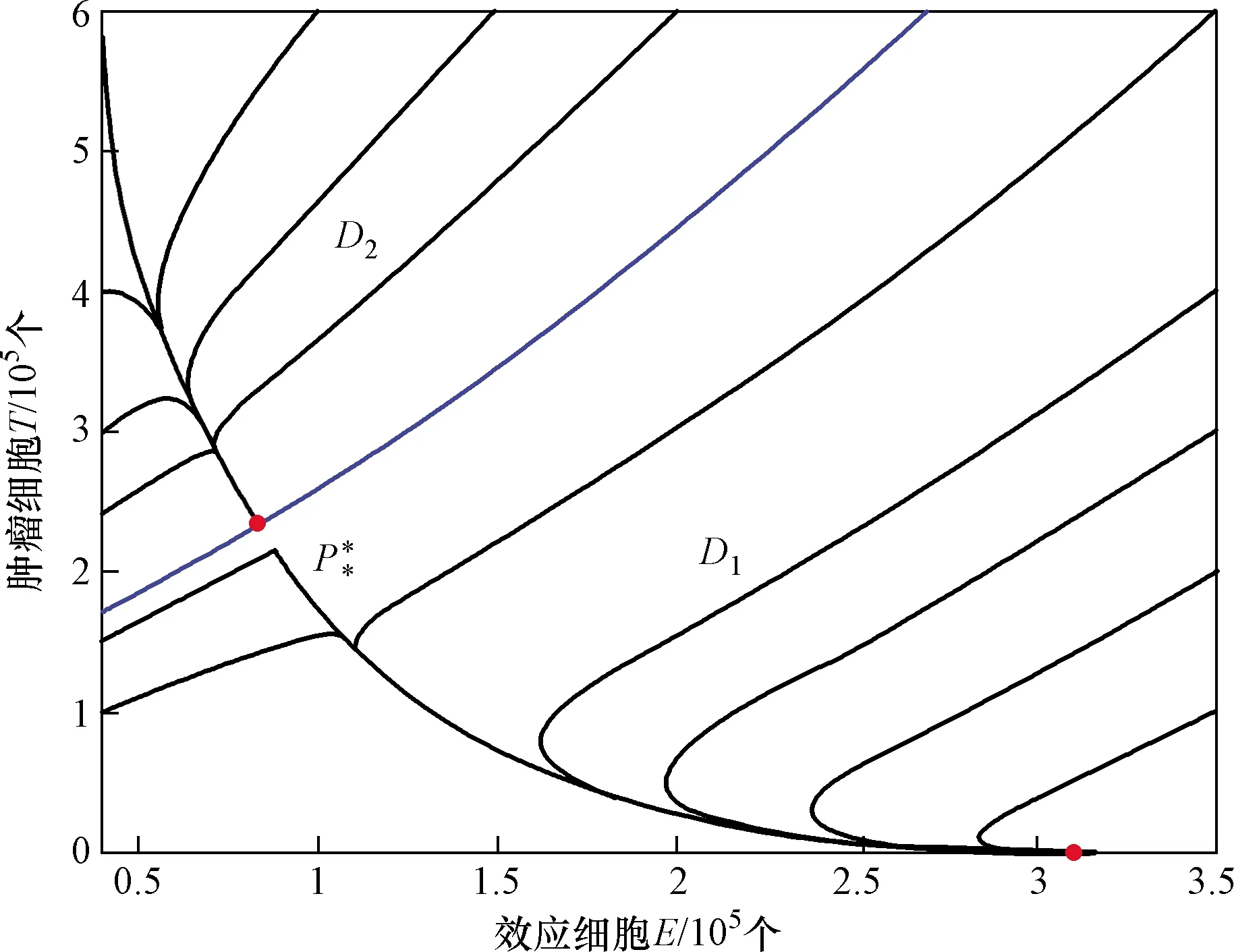
為模型的有瘤平衡點圖3 式(2)存在正平衡點P**時的情形Fig.3 The case of formula (2) with positive equilibrium P**

藍色線表示P*的穩(wěn)定流形圖4 式(2)存在兩個正平衡點時的情形Fig.4 The case of formula (2) with two positive equilibrium

3 數值模擬

為了直觀地展示理論分析的正確性，對式(2)進行數值模擬。選取如下參數值：s=1.3×104，c=6.7×10-9，μ=0.0412，ε=1×107，r=1.5×10-1。

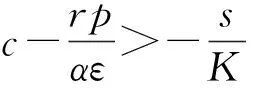
(2)取參數值p=5，α=1.041×10-7，K=570 000。此時R0=4.57>1，式(2)有唯一正平衡點P*(4.3×104,5.5×105)，且該點在區(qū)域D內是全局漸近穩(wěn)定的(圖2)。

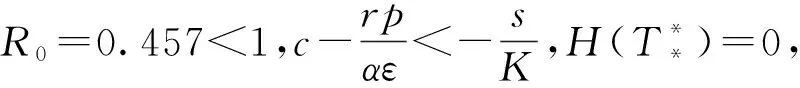
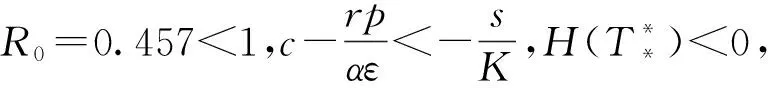
將分析腫瘤細胞對效應細胞的抑制率系數p和效應細胞對腫瘤細胞的抑制率系數α對模型動力學行為的影響。

首先,當s=1.3×104，c=6.7×10-9，μ=0.041 2，ε=1×107，r=1.5×10-1，α=1.041×10-7，K=570 000時，取p分別為0、4、8、12、16。由圖5可以看到，當p=0時，腫瘤細胞的數量處于最低水平，而效應細胞的數量處于最高水平。當p增大時，腫瘤細胞的數量會隨著腫瘤對效應細胞的抑制率系數p的增大而增加，而效應細胞的數量會隨著p的增大而減少。其次，當s=1.3×104，c=6.7×10-9，μ=0.041 2，ε=1×107，r=1.5×10-1，p=5，K=570 000時，由圖6可以看到，隨著效應細胞對腫瘤細胞的抑制率系數α的增大，腫瘤細胞的數量逐漸減少，而效應細胞的數量逐漸增加，當α=15×10-7時，腫瘤細胞的數量減少到0，也即此時腫瘤會滅絕。

圖5 腫瘤細胞對效應細胞的抑制率系數p對模型動力學行為的影響Fig.5 Effects of the inhibition coefficient p of tumor cells to effector cells on the dynamics of the model

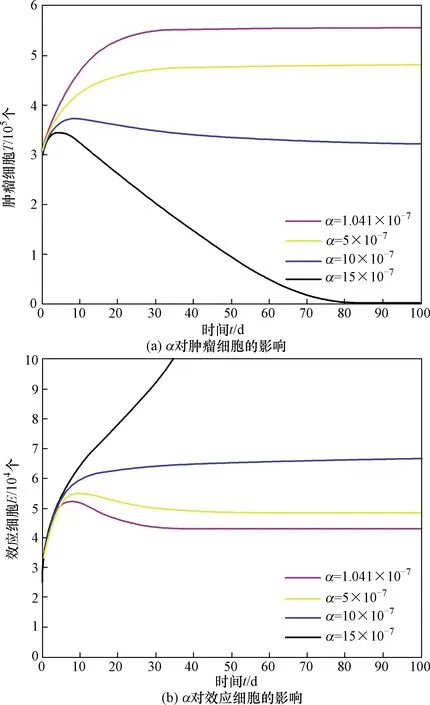
圖6 效應細胞對腫瘤細胞的抑制率系數α對模型動力學行為的影響Fig.6 Effects of the inhibition coefficient α of effector cells to tumor cells on the dynamics of the model

4 結論

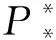
通過觀察腫瘤細胞對效應細胞抑制率系數與效應細胞對腫瘤細胞抑制率系數的變化對模型的影響(圖5,圖6)可得到如下結論。

(1)可以通過一些方法來降低腫瘤細胞對效應細胞的抑制率系數，逆轉免疫抑制狀態(tài)，提高免疫效應細胞對腫瘤細胞的殺傷力。

(2)增大效應細胞對腫瘤細胞的抑制率對腫瘤的清除有良好的效果。