基于劃分的數據挖掘K?means聚類算法分析

曾俊

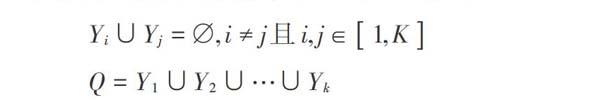
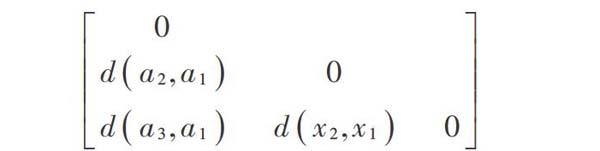
摘? 要： 為提升數據挖掘中聚類分析的效果，在分析數據挖掘、聚類分析、傳統K?means算法的基礎上，提出一種改進的K?means算法。首先將整體數據集分為[k]類，然后設定一個密度參數為[?]，該密度參數反映數據庫中數據所處區域的密度大小，[?]值與密度大小成正比，通過密度參數優化[k]個樣本數據的聚類中心點選取;依據歐幾里得距離公式對未選取的其他數據到各個聚類中心之間的距離進行計算，同時以此距離為判別標準，對各個數據進行種類劃分，從而得到初始的聚類分布;初始聚類分布得到之后，對每一個分布簇進行再一次的中心點計算，并判斷與之前所取中心點是否相同，直到其聚類收斂達到最優效果。最后通過葡萄酒數據集對改進算法進行驗證分析，改進算法比傳統K?means算法的聚類效果更優，能夠更好地在數據挖掘當中進行聚類。

關鍵詞： 數據挖掘; 聚類分析; K?means聚類算法; 聚類中心選取; K?means算法改進; 初始中心點

中圖分類號： TN911.1?34? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼： A? ? ? ? ? ? ? ? ? ? ? ? ? 文章編號： 1004?373X（2020）03?0014?04

Analysis of partition?based data mining K?means clustering algorithm

ZENG Jun

（College of Big Data and Intelligent Engineering， Yangtze Normal University， Chongqing 408100， China）

Abstract： An improved K?means algorithm on the basis of the analysis of data mining， clustering analysis and traditional K?means algorithm is proposed to improve the effect of clustering analysis in data mining. The whole data set is divided into [k] classes firstly， and then a density parameter [?] is set， which reflects the density of the area in which the data is located in the database. The value of [?] is proportional to the density. The selection of cluster center points of [k] sample data is optimized by the density parameter. The distance between other unselected data and each cluster center is calculated by Euclidean distance formula. At the same time， the distance is taken as the criterion to divide each data into different categories， so as to get the initial clustering distribution. After the initial clustering distribution is obtained， the center point of each distribution cluster is calculated again to judge whether it is the same as the previous center point， until the clustering convergence reaches the optimal effect. Finally， the wine algorithm is used to verify and analyze the improved algorithm. The results show that the improved algorithm has better clustering effect than the traditional K?means algorithm， and can better perform clustering in data mining.

Keywords： data mining; clustering analysis; K?means clustering algorithm; clustering center selection; K?means algorithm improvement; initial center point

0? 引? 言

信息時代的來臨及其快速發展為人們的生活與工作帶來了極大便利，數據資源對于人們的影響也越來越大。如何從龐大繁雜的數據資源當中汲取有效信息變得極其重要，數據挖掘應用而生。聚類分析在數據挖掘模型當中的作用巨大。基于劃分的K?means算法是聚類分析中具有代表性的算法，其收斂性相對較強，但傳統的K?means仍存在諸多問題，對于K?means算法應當如何改進，怎樣通過算法融合和各類技術手段進行優化，很多專家學者對此相當關注。當前K?means算法主要存在的缺陷主要是樣本數據[k]值的選擇，孤立點的影響仍然難以消除等。同時，K?means算法計算量相對較大，需要承擔較大的計算壓力。本文提出通過設定密度參數進行初始中心點的優化，從而進行聚類分析，做到更好的數據挖掘效果。

1? 數據挖掘概述

1.1? 數據挖掘的現狀

總體來看，數據挖掘所要研究的數據大致可以分為半結構化數據、結構化數據、非結構化數據以及異構數據等[1]。

隨著信息技術翻天覆地的發展與進步，數據挖掘以及人工智能在生產生活當中的位置愈發重要。無論是工業生產還是日常生活，都能夠通過數據挖掘帶來更好的利益與便利，更好地提高人民的生產生活水平。

1.2? 數據挖掘的流程

數據挖掘的一般流程如下簡述：

1） 對數據進行選擇以及集成，是指從已有的數據庫當中進行相應的目標數據選取，并以此作為下一步的處理目標。

2） 對所選數據進行預處理，是指對所選數據當中的重復部分以及噪聲做出消除，同時對缺失數據進行計算彌補。數據的預處理是整個數據挖掘過程當中的關鍵一步，其中步驟不需要順序排列，同時可以多次執行以達到所求效果。

3） 數據的轉化，數據轉化的過程是將步驟2）所得數據進行對應實際需求的轉化，如多維到低維的轉化，通過轉化達到數據挖掘更為高效的目的。

4） 相關數據挖掘的算法，依據聚類、回歸、概括或者分類等各種模型的建立，做出對應的數據建模。

5） 對數據做出進一步的評估，以獲得有價值的結論，提供實用信息。

2? 聚類分析簡述

2.1? 聚類分析的定義

聚類分析是指對整體的數據庫依據一定算法進行分析與計算，將其進行類別劃分，同類當中的數據具備盡量大的相似性，不同類之間的差異性盡可能大[2]。具體表達上，整體數據可以定義為集合[N]，[N=x1，x2，…，xn]，其中，[n]表示整體數據中的數據量。在對整體數據庫[N]進行聚類時，把數據庫[N]中的[n]個數據依照目標相似度進行劃分，劃分為[m]類[y1，y2，…，ym]，其中，[yi]為劃分的第[i]類，聚類結果用集合[Q]表示，表達式如下：

2.2? 聚類分析的現狀

聚類分析目前已經應用到各類領域，其中難點是算法的普適性以及有效性的提升[3]。這主要是由于當前信息時代越來越大的數據分析需求。同時，聚類分析作為以距離為主要分析依據的劃分技術，理論依據是統計學與機器學習。當前聚類分析的發展中，由于需要面對越來越龐雜的數據量，聚類分析往往存在一定缺陷，難以實現高效和精準。大數據時代數據的差異性也決定了很難找到一個普適的聚類算法對所有數據進行分析。

多數聚類算法與爬山算法有一定的相同之處，其缺點主要表現在兩個方面：一是容易產生局部最優;二是數據量過大時，往往難以聚類精準。因此，聚類算法仍然需要不斷的完善與改進，以適應更大更復雜的數據處理。具體上，可以通過學科互補進行聚類分析的優化。如以混沌理論作為基本依據的聚類分析或者是借助各類優化算法所進行的聚類分析[4]。

2.3? 聚類分析的流程

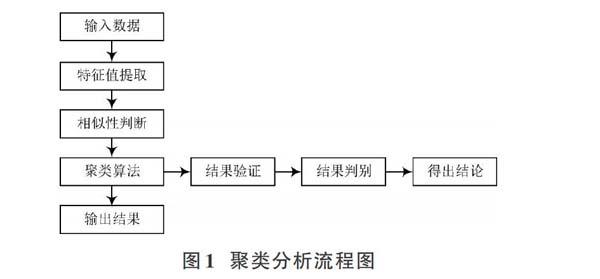
聚類分析旨在理清整體數據，首要工作是整體數據的選擇，并從中進行信息提取。在此過程中，歐幾里得空間距離是其相似性的基本判斷依據。相似性判斷之后，進行對應的結果驗證[5]。通常結果驗證需要進行多組數據的檢驗，以提高其普適性。聚類分析具體的流程如圖1所示。

2.4? 聚類算法的數據結構

聚類算法的數據結構主要分為兩類：一類是相異度矩陣;另一類是數據矩陣。下面對兩類數據結構做簡單介紹。

2.4.1? 相異度矩陣

相異度矩陣主要體現樣本數據之間的差異性，其作為對象?對象的一種數據表達方式，是多種聚類算法的底層基礎。當樣本數據為[m]時，其相異度矩陣為[m×m]維，所表達的是[m]個樣本數據的差異性。對于含[m]個樣本數據的數據庫集合[N=a1，a2，…，an]來說，其相異度矩陣可以表示為：

式中[d（i，j）]是樣本數據[i]與樣本數據[j]之間的量化表示，多數情況下，此值非負。若兩個樣本數據之間的相似度越高，則此值相應越小;若兩個樣本數據之間的相異度越高，則此值越大。

2.4.2? 數據矩陣

數據矩陣能夠對整體數據當中的所有樣本數據的屬性值進行表示。其數據樣本以行表示，數據的屬性以列表示。如數據庫所組成的集合[Q=a1，a2，…，an]，其對應的數據對象[ai]若有[m]個屬性，則表示其維度為[m]，矩陣表示如下：

3? K?means聚類算法簡述

3.1? K?means算法研究現狀

K?means聚類算法自提出至今，有關于此類算法的研究有很多。同時在工商業、科學、統計學以及人工智能等各個領域有廣泛的應用。當下比較熱門的微博熱點的提取、銀行中客戶信息的整理以及圖形處理等方面都會應用到K?means聚類算法。近年來，關于K?means算法的優化算法多種多樣，同時學者們也對K?means算法做出了進一步的完善，如通過聚類評價指標的更新獲得更好的聚類結果;利用學科融合，K?means算法與粒子群相結合或是K?means算法與神經網絡相結合的算法等[6]。

3.2? K?means算法的基本思想與實現步驟

K?means算法是基于劃分的一類經典的聚類算法，此類算法能夠在[n]維的數據空間中進行廣泛應用。K?means算法通過多次迭代對給定的樣本數據進行不同的種類劃分，劃分的每一種類的內部數據盡可能相似，與其他種類的數據盡可能相異。K?means算法的基本思想是：首先將整體數據集分為[k]類，并從整體數據集當中選取[k]個樣本數據作為最初的聚類中心;最初聚類中心確定之后，依據歐幾里得距離公式對未選取的其他數據到各個聚類中心之間的距離進行計算，同時以此距離為判別標準，對各個數據進行種類劃分，從而得到初始的聚類分布。初始聚類分布得到之后，對每一個分布簇進行再一次的中心點計算，并判斷與之前所取中心點是否相同，若不同，則進行新的迭代調整，直到其聚類收斂能夠達到研究所需，停止迭代，結束算法。K?means聚類算法進行聚類的過程是通過迭代計算對中心點進行更好確立的過程。此類算法往往簡便易行、效率較高，同時收斂速度很快。其具體步驟簡述如下：

1） 設整體數據集為[N]，在數據集[N]中選擇[k]個樣本數據，這[k]個樣本數據定義為最初聚類中心，得到[M1]，[M2]，…，[Mk]個最初的聚類中心點，以此區別劃分種類的數量。

2） 對數據集合中未選取的樣本數據到各個聚類中心點間的距離進行計算，并依據距離進行樣本數據的劃分，形成初始的聚類分布。

3） 以公式[Mi=1nix∈φiN]為計算依據，對各個聚類簇進行再一次的中心點計算，所得到的新的中心點用[Mn1，Mn2]，…，[Mnk]表示。

4） 判斷是否符合目標收斂度，若不符合，則返回步驟2），直到滿足目標收斂度為止。

5） 輸出所得的聚類數據。

K?means算法的流程圖如圖2所示。

4? 優化中心點對K?means算法進行改進

4.1? 提出問題

K?means算法是否能夠產生更好的聚類效果，在很大程度上取決于初始中心點的選取。原有的K?means算法在進行初始中心點選取時，無法確定中心點選取是否整體分散，抑或中心點是否會選擇到噪聲數據或者是邊緣數據。其聚類結果的時效性以及穩定性無法得到保障。具體應用當中，找到合適的中心點能夠幫助K?means算法達到效果最優。

K?means算法的中心點選取時，受數據分布影響會產生較大誤差，可參照圖3進行分析。

圖3中，a）與b）中心點與其中部分對象的歐氏距離相同，但是二者的整體分布存在差異;b）與c）的整體分布大致相同，但是個別點與中心點的距離不同。在中心點的選取過程當中，個別中心點選取所反映的整體數據分布存在差異。如何選取一個合適的中心點，更好地處理整體數據分布，反映數據聚類信息，是解決中心點選取的關鍵。

4.2? 通過密度參數優化中心點選取

可以設定一個密度參數為[?]，該密度參數反映數據庫中數據所處區域的密度大小，[?]值與密度大小成正比。此值通過以選定的樣本數據[ai]作為中心，將與其距離相近的[n]個參數到此對象的距離平均值作為[?]值。主要的算法依據是：首先通過歐幾里得空間距離進行樣本數據之間的距離計算;而后對各數據的密度參數[?]值進行計算，并計算[?]值的平均值[?]。所有密度參數值組成集合[D]。[k]個初始中心點從集合[D]中進行選取，而后進行基于K?means算法的聚類分析。從集合[D]中選取[k]個初始中心點的步驟如下：

1） 在密度集合[D]中選擇最小密度參數值[?]所對應的樣本數據，以此作為首個聚類中心點[ai（i=1）]。

2） 集合[D]刪除[?]半徑內的數據與中心點[a1]。

3） 令新的密度集合為[D]，并計算密度參數[?]。

4） 執行步驟1），得到聚類中心點[ai]。

5） 判斷[i]是否等于[k]，若是，則輸出[k]個中心點。否則，返回步驟2）。

中心點選取的具體流程如圖4所示。

中心點選取完畢后，依照K?means算法的步驟進行聚類分析。

4.3? 結果驗證與分析

通過Wine葡萄酒數據集對改進算法進行驗證分析。Wine葡萄酒數據集包括3種起源不同的葡萄酒的178條記錄。同時，包含13個不同屬性，表示葡萄酒的13種不同化學成分。實驗采用傳統K?means算法改進后的算法相對比的方式進行，并得出對應的實驗結果。實驗結果如表1所示。

通過實驗結果不難發現，K?means算法的聚類結果不夠穩定，其準確度多數低于改進算法。同時，K?means算法的準確度均值要低于改進算法。實驗結果證明，改進算法比K?means算法的聚類效果更優，能夠更好在數據挖掘當中進行聚類分析。

5? 結? 語

針對傳統K?means算法中心點選取的不足之處，借助密度參數對中心點選取進行優化。經過實驗對比分析，改進算法比傳統K?means算法的聚類效果更優，能夠更好地在數據挖掘當中進行聚類。

參考文獻

[1] 李國杰，程學旗.大數據的研究現狀與科學思考[J].中國科學院院刊，2012，27（6）：647?657.

[2] 黃敏，何中市.一種新的K?means聚類中心選取算法[J].計算機工程與應用，2011，47（35）：132?134.

[3] 劉兵，夏世雄，周勇.基于樣本加權的可能性模糊聚類算法[J].電子學報，2012，34（5）：1332?1335.

[4] 鄭丹，王潛平.K?means初始聚類中心的選擇算法[J].計算機應用，2012，32（8）：2186?2188.

[5] 金曉民，張麗萍.基于最小生成樹的多層次K?means聚類算法及其在數據挖掘中的應用[J].吉林大學學報（理學版），2018，56（5）：153?158.

[6] 龔敏，鄧珍榮，黃文明.基于用戶聚類與Slope One填充的協同推薦算法[J].計算機工程與應用，2018，54（22）：144?148.

[7] WANG Zhiqiong， XIN Junchang， YANG Hongxu. Distributed and weighted extreme learning machine for imbalanced big data learning [J]. Tsinghua science and technology， 2017（2）： 160?173.

[8] LI Peng， LUO Hong， SUN Yan. Similarity search algorithm over data supply chain based on key points [J]. Tsinghua science and technology， 2017（2）： 174?184.

[9] DAN Tao， LIN Zhaowen， WANG Bingxu. Load feedback?based resource scheduling and dynamic migration?based data locality for virtual Hadoop clusters in OpenStack?based clouds [J]. Tsinghua science and technology， 2017（2）： 149?159.