面向位置敏感器件的反饋堆疊信號濾波

崔 昊，郭 銳，李興強*，馮克建，張飛飛

(1.中國科學院 沈陽自動化研究所 智能檢測與裝備研究室，遼寧 沈陽 110016；2.中國科學院 機器人與智能制造創新研究院，遼寧 沈陽 110169；3.中國科學院大學，北京 100049；4.西安航天發動機有限公司，陜西 西安 710100)

1 引 言

位置敏感器件(Position Sensitive Devices，PSD)是一種光電位置探測器，屬于半導體器件。與其他使用離散探測陣列方式的傳感器(如CCD[1]等)不同，PSD是由一個整體的PIN光電二極管組成，利用光電二極管表面阻抗分布均勻的特性可實現光點位置信息的快速連續采集[2]；此外，PSD的輸出僅與光點位置有關，與光強度無關，響應速度快，位置分辨率高，因此廣泛應用于位移檢測、角度測量等領域。在實際應用中，由PSD及其外部信號處理電路所采集的信號夾雜著大量噪聲，如何獲得準確穩定的位置信號成為了使用PSD要解決的關鍵問題之一[3]。PSD信號產生誤差的來源主要有三點：第一，在PSD的光敏區域內，光點位置與光電流輸出并非完全呈線性，隨光點位置勻速偏離PSD中心，光電流信號的非線性度增大；第二，PSD輸出信號微小，在后續信號放大等處理過程中易受各分立元件帶來的非線性因素和噪聲因素影響，從而降低測量精度；第三，在不同應用場合下，環境光或應用條件的影響可能導致光斑的強度分布不均勻，從而影響PSD的位置識別精度[4]。

傳統的PSD信號處理方法除了簡化電路設計、硬件的采樣保持濾波外，軟件的數字濾波算法是實現各種非理想因素補償的重要方法[5-8]。陳健等[9]通過結合基于閾值的自適應中值濾波方法與多閾值自適應濾波算法，提出了一種兩階段結合的方法，提高了對數據細節的保護能力。但該方法只適用于中低噪聲密度的對象；N Agrawal等[12]針對復雜度大的處理對象，使用粒子群優化算法和人工蜂群算法設計出一種穩定的IIR(Infinite Impulse Response)數字濾波器，解決了在通帶和阻帶區域濾波均方誤差的非線性最小化問題，但增加了數據處理的成本；楊媛等[11]結合最小二乘法與滑動平均濾波的優點，提出了一種改進型濾波算法，在未引入龐大計算量的前提下，對信號的識別和檢測取得了可靠效果；除此之外，Zhao等[12]設計了一種基于正弦函數的新型數字濾波器，具有抑制噪聲、抗彈道損失和提高能量分辨率等優勢，同時簡化了結構、提升了可操作性；Rajib Kar[13]在硬件上實現了分數階模擬濾波器，如Butterworth濾波器，提供了阻帶衰減的精確控制；葉國陽等[10]根據數據噪聲的特點，提出了一種中值濾波和小波濾波相結合的方法，在消除奇異噪聲方面取得了良好效果。但由于奇異噪聲通常無規律可尋，多數傳統方法濾波效果的精確度欠佳。

對于數字信號的濾波，現有的方法主要是在真實結果未知的條件下，依據被處理數據在時域或頻域上的分布特性，給定預期的處理指標，通過計算得到。而在實際應用中，例如傳感器的調試、模擬信號的調制等，目標真值通常是可獲得的，若能夠充分地利用目標真值求取其與待處理數據間的關系，則既簡化了數據的處理過程，又能夠提高精度。此外，高速測量下的PSD采集信號具有樣本數目有限、非線性度高等特點，而傳統濾波方法往往需要大量的測量樣本來支撐結果的準確性，使得傳統方法的處理結果不佳。

針對上述問題，本文提出了一種以ELM(Extreme Learning Machine)為基本預測模型的反饋堆疊學習算法FsELM(Feedback stacking modle based on ELM)，在保持ELM快速學習和良好泛化能力的前提下，提高了預測精度并具有良好的魯棒性。該算法通過將預測值與真實值的偏差作為反饋并更新輸入數據，構造了反饋堆疊模型，實現了數據的多層深度訓練。為驗證所提出模型的有效性和實用性，進行了基于一維PSD的激光三角位移信號處理驗證實驗，與傳統的小波濾波方法以及IIR數字濾波算法對比后，證明了FsELM在處理隨機噪聲干擾信號的優越性，與經典學習算法、核函數處理的ELM及ELM的變體進行了比較，證明了FsELM在預測精度上有所提升。

2 ELM原理

ELM是一種用于分類和回歸的單隱層前饋神經網絡的學習算法[15-17]。ELM在進行模型訓練時會根據所設置的隱藏層節點數目自動生成隨機數權重矩陣和偏置，這使得整個訓練過程中沒有權重迭代變化的存在，在保證網絡具有良好泛化能力的同時，極大程度地提高了前向神經網絡的學習速度，避免了基于梯度下降學習方法存在的許多問題[18]。

在實際應用中，ELM首先進行模型訓練，訓練數據包括目標真實結果和與之對應的若干影響因素。記錄訓練后的輸入層權重、偏置以及隱藏層權重用于ELM的預測，預測時輸入與訓練數據結構相同的影響因素即可得到預測結果。具體地，ELM通過式(1)將輸入數據映射到L維的隨機特征空間：

(1)

其中：β=[β1，β2，…，βL]T表示處于隱藏層節點和輸出節點間的隱藏層權重矩陣。h(x)=[h1(x)，h2(x)，…，hL(x)]表示L個隱藏節點對應于輸入x的輸出行向量，h(x)構成輸入數據到隱藏層輸出的映射矩陣H。ELM等式可以總結為：

Hβ=T，

(2)

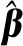
(3)

其中H?表示矩陣H的廣義逆矩陣。

3 反饋堆疊極限學習機

一維PSD的輸出信號微弱，且信號的傳輸過程中存在如器件自身誤差、信號處理電路噪聲以及實驗條件影響等干擾，原始數據的有效信息被湮沒于大量噪聲中。ELM僅具有單隱層結構，而增大隱藏層節點數目并不能提高預測能力的上限，過多的隱藏層節點還可能造成模型的過擬合。因此通常需要多隱藏層結構或多層次訓練來提取數據的潛在相關。Yu等[19]嘗試用深度堆疊泛化的思想改進極限學習機并設計了一種深度堆棧極限學習機(DrELM)。該方法使用ELM作為單次訓練模型，將ELM的預測結果與隨機數矩陣相乘并激活后與原始數據相疊加作為下一層的輸入，以此類推循環訓練。DrELM提供了一種使用ELM進行多層訓練的新思路，并提升了模型預測能力。本文對ELM的多層訓練結構在迭代的實現方式上進行了改進，進一步提升了算法的預測精度。

受控制理論中“反饋”思想和深度迭代學習思想的啟發[20-21]，本文提出了一種基于經典ELM的反饋堆疊學習算法(FsELM)，在保持ELM快速訓練和優秀泛化能力的同時，提升了預測結果的準確性并具有良好的魯棒性，實現了PSD信號有效信息的深度提取。該學習算法將單次訓練后的結果與目標真值再次做差，通過隨機映射、核函數激活以及合適的反饋因子，與相鄰最近的ELM訓練塊的輸入數據疊加作為下一層訓練的輸入，模型的訓練結構如圖1所示。FsELM算法充分利用了目標真實值，而非單純地利用單層訓練結果作為反饋項，使原始數據的迭代變化更有意義。

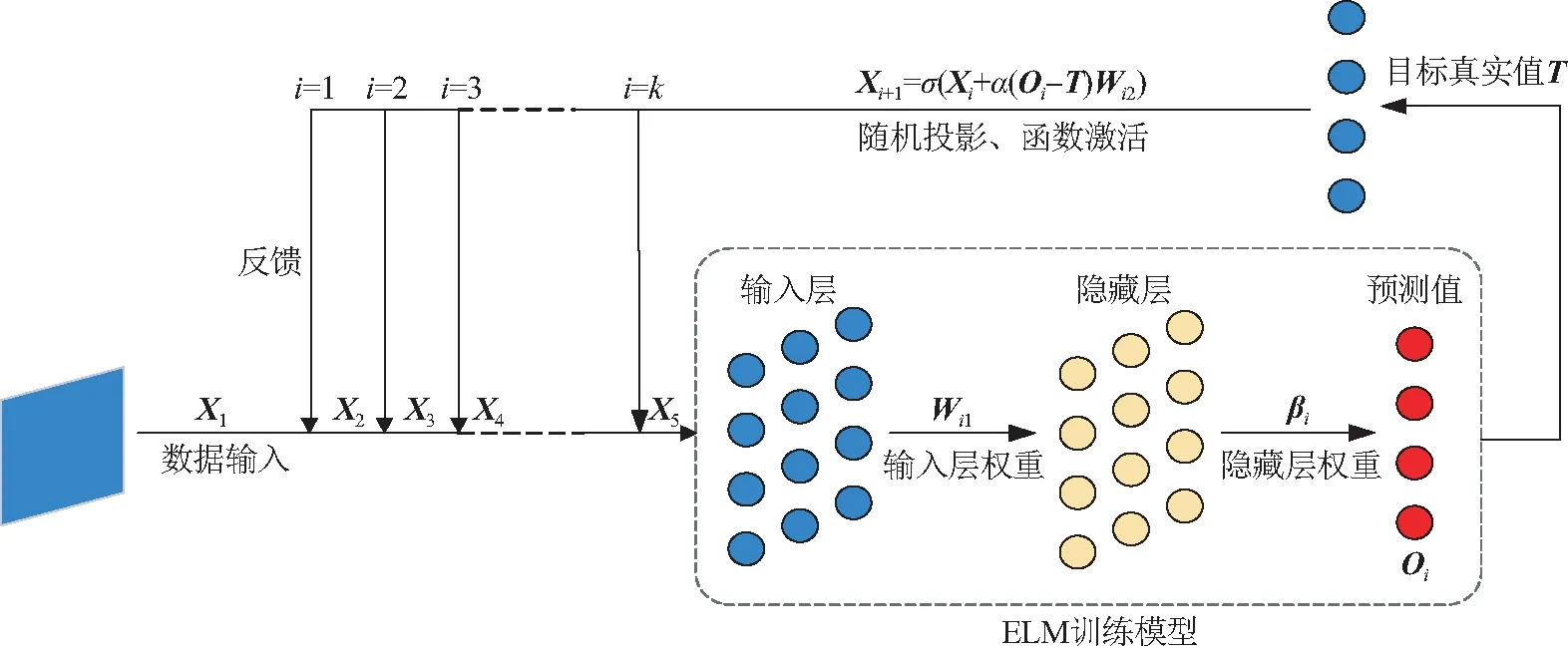
圖1 FsELM反饋訓練結構示意圖

在實際應用中，選取一個包含m組的訓練集(xi，ti)，其中xi∈Rd(d表示相關影響因素的維數)表示特征向量，ti∈Rc(c表示目標真值維數)表示與xi相對應的目標真值。定義矩陣X為包含m個輸入數據樣本的矩陣，矩陣T為目標真值矩陣，即X=[x1，x2，…，xm]T，T=[t1，t2，…，tm]T，以此進行單層ELM的訓練。訓練可得一組初步的預測結果O=[o1，o2，…，om]T，該結果不會精確逼近目標真值，但會優于隨機猜測。對于堆疊模型的實現，利用預測結果與真實結果的差值O-T作為反饋項，通過式(4)計算得到Xi+1作為下一層訓練的輸入(假定上一層訓練的輸入為Xi)：

Xi+1=σ(Xi+α(Oi-T)Wi2)，

(4)

其中：α為反饋因子，表示反饋信號與輸出信號之比，Wi2∈Rc×d為服從正態分布的隨機數矩陣。核函數σ(·)可為任意激活函數(如sigmoid函數、高斯函數、三角函數等)。反饋過程采用了與ELM類似的隨機映射的思路，無需進行權重的更新，保證了算法運行過程的速率。

(5)

綜合FsELM的訓練和預測過程，繪制如圖2所示的學習算法流程圖。

圖2 FsELM學習算法流程圖Fig.2 Flowchart of FsELM algorithm

4 測量實驗與結果

為證明本文所提出算法在預測性能上的提升，設計了基于一維PSD的激光三角位移檢測實驗并采集了相關數據，與傳統的信號濾波方法以及經典學習算法、核函數處理的ELM及ELM的變體進行了比較。

4.1 位置敏感器件(PSD)結構與光電流計算

PSD主要由單表面或雙面附有電阻層的一個高阻抗半導體層構成，電阻層兩端放置一對電極，用于輸出位置信號。電阻層上的光敏區域是一個PN結，通過光電效應產生光電流。圖3為PSD的剖面圖，在N型高阻硅基底上設有P型電阻層，作為光電轉換的活動區域，且兩端設有一對輸出電極。N型硅基底連接有公共電極。因此，除了表面的P型電阻層外，這與PIN型光電二極管的結構相同。

圖3 PSD剖面示意圖Fig.3 Diagrammatic profile of PSD

當有光束照射時，PSD上的不同位置就會產生與光強成比例的電荷，該電荷流經電阻層并被輸出電極X1和X2收集為光電流，該光電流與入射位置和每個電極之間的距離成反比。假設PSD中點為原點，入射光位置與輸出電極的光電流之間的關系式為：

IX1=IO·(LX/2-XA)/LX，

(6)

IX2=IO·(LX/2+XA)/LX，

(7)

(8)

(9)

其中：IO為總光電流IX2+IX1；IX1為電極X1的輸出電流；IX2為電極X2的輸出電流；LX表示阻抗長度；XA表示光點距PSD中點的距離。

4.2 位移檢測實驗

激光三角法[22]是一種非接觸式光電測量方法，由于其測量高效、準確和無損傷等優勢被應用于位移、角度、振動等多類測量領域。其原理為：激光器發出的一束激光照射在待測物體平面上，接收物鏡采集物面的漫反射光并在檢測器上成像，該像的位置會隨著物體表面沿入射光方向的位置變化而變化。通過像移和物體位移之間的關系式，可由像移大小計算出物體的實際位移。

根據激光三角法原理繪制出如圖4所示的位移檢測光路圖，并設計了激光三角傳感器。實驗中，干涉儀鏡組固定于被測物面一側并放置在滑軌上，固定有鏡組的一側放置激光干涉儀，另一側為激光三角傳感器，檢測模型如圖5所示，現場實驗如圖6所示。開始實驗前移動被測物面直到PSD輸出為0，同時將激光干涉儀調零。為了保證PSD的采集數據可以提供同一位置盡可能多的信息，設置傳感器重復采集同一位置信號40次，并以激光干涉儀測得數據作為目標真值。實驗時，將被測物面以10 μm左右的間隔平移約2 mm，分別記錄每次移動后激光干涉儀和與之對應的傳感器的輸出。

圖4 位移檢測光路示意圖Fig.4 Optical path of displacement detection

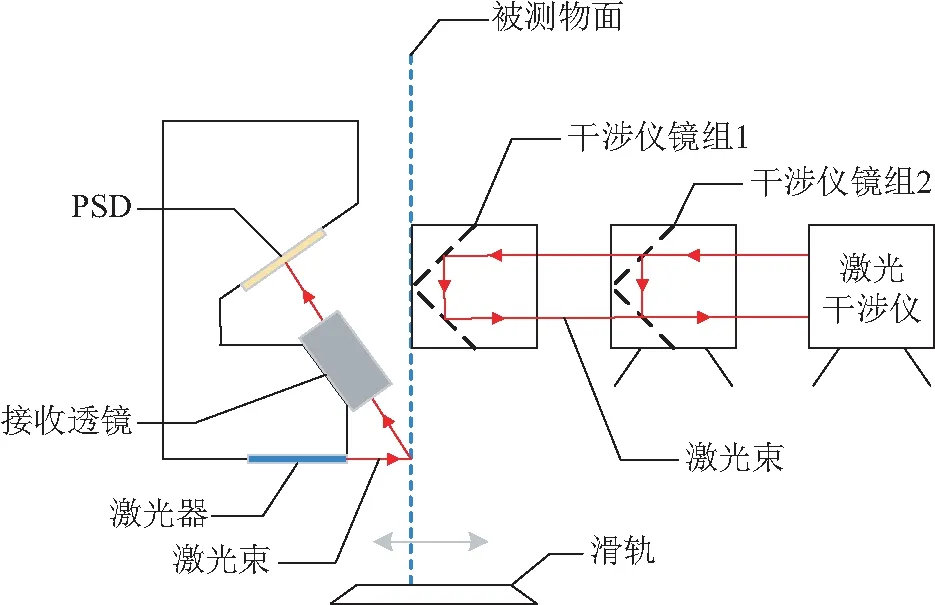
圖5 位移檢測模型示意圖Fig.5 Displacement detection model

圖6 位移檢測現場示意圖Fig.6 Displacement detection site

4.3 實驗驗證與結果分析

4.3.1 實驗方法

實驗采用一只激光三角傳感器進行三次獨立的位移測量實驗(光斑從設定量程的一端間隔地遍歷PSD光敏面至另一端算作一次獨立實驗)。根據前文的介紹，一次獨立的實驗采集約n=200組數據，數據集結構為X(n，40)和T(n，1)。采用4折交叉驗證的方法進行最優模型和參數的評估，隨機的將樣本數據分為四部分，分別選取其中三部分作為訓練集，其余為測試集，即每次獨立實驗進行4次模型預測。

FsELM模型網絡的參數包括隱藏層節點個數L和模型深度k。其中，模型深度為1時，該算法模型等同于經典ELM。實驗中設定α=0.1，激活函數為“sigmoid”函數，分別設置隱藏層個數為5～100(間隔為5)，模型深度為1～9，共有180種組合。通過計算預測結果與目標真值的均方誤差對預測精度進行定量的評估。均方誤差(Mean Squared Error，MSE)的計算方法為：

(10)

其中：observed表示預測結果，predicted表示目標真值。每種組合下重復預測150次，計算MSE的均值和方差(方差用來評估學習算法的預測穩定度)。

表1 4折交叉驗證結果與網絡參數Tab.1 Results of 4-fold cross validation and network parameter

如表1所示為FsELM預測模型的4折交叉驗證實驗結果與對應的網絡參數。分析可知，在進行三次獨立實驗中的多次預測結果相近，最優預測MSE的均值分別為1.25×10-5，2.51×10-5，1.1×10-5，計算最優隱層節點個數的均值為68，平均模型深度為6。如此設定FsELM模型的網絡參數，并進行對比實驗的驗證。

4.3.2 對比實驗

為評估算法性能，選擇了具有代表性的傳統濾波算法和經典學習算法進行了對比實驗，并作出定性分析。

傳統的數據處理方法包括數據預處理、濾波、最小二乘法擬合三個過程。預處理過程處理的對象是對同一位置的重復測量數據，分別采用自適應中值濾波(Adaptive Median Filter，AMF)[4]和直方圖統計預處理(HS)[23]。

濾波過程采用小波濾波(Wavelet Filter，WF)[5]和巴特沃斯IIR低通濾波(IIR)[8]進行處理濾波參數如下：

(1)IIR：通帶截止頻率200π；阻帶截止頻率2 000π；通帶衰減不大于1 dB，阻帶衰減不小于8 dB；

(2)WF：利用小波“db5”對數據進行7層分解，將小波分解的前3層高頻系數置零，后4層采用軟閾值函數處理，設定閾值為0.014。

預處理和濾波方法兩兩組合為4種不同的處理方法，最后使用最小二乘法擬合真實位置曲線。

神經網絡比較算法包括支持向量回歸機(Support Vactor Regression，SVR)、原始ELM(ELM)[10]、核函數處理的ELM(K-ELM)、堆棧ELM(DrELM)[17]。參數設置如下：

(1)SVR：核函數選用徑向基函數；懲罰系數為2.2；損失函數p的值為0.01；

(2)ELM，K-ELM，DrELM中隱層節點個數分別為5，4，5，其中DrELM模型深度為2。

表2 FsELM與其他數據處理方法的結果對比Tab.2 Comparison of results between FsELM and other digital processing methods (×10-4)

對比實驗的結果如表2所示，分析實驗數據可知：ELM，K-ELM和DrELM的處理效果與采用傳統的預處理和濾波相結合的方法相近，而FsELM的預測結果更為精確。這是由于對同一位置進行重復測量的數據所受噪聲干擾是隨機的，傳統的處理方法無法根據噪聲的規律進行數據處理。FsELM算法能夠獲取噪聲的潛在相關，在應對隨機干擾時表現出更優異的性能。

同時，FsELM相比ELM，K-ELM和SVR，預測精度上有大幅提升，表明了堆疊訓練結構在處理復雜回歸問題時可獲取更精確的結構信息，與DrELM的結果對比表明，與目標真值的偏差反饋更有助于模型對結構信息的學習。

4.3.3 時間復雜度分析

神經網絡的時間復雜度正比于模型的運算次數，對于單隱層神經網絡，時間復雜度可由式(11)表示：

Time～O(k(n1×L+L×n3))，

(11)

式中：k表示模型訓練深度；L表示隱層節點個數；n1和n3分別代表輸入樣本個數和輸出樣本個數。對于相同數據集的預測，時間復雜度簡化為O(k×L)。FsELM是一種堆疊式結構，理論上相比ELM等單層模型具有較高的復雜度，但FsELM使用ELM作為單層訓練模型，保留了ELM無需迭代更新權重的優勢，使得運算過程相比于其他神經網絡模型更簡便。本節在公共測試集中選取相同訓練集和測試集且所有的算法保持原算法的參數設置以保證實驗公平性，對4.3.2節中對比方法的數據處理時間進行統計。計算機硬件配置為Inter Core i7-4720HQ，2.6 GHz，8 G RAM，軟件平臺為MATLAB R2016a。

圖7 模型運算時間對比Fig.7 Comparison of processing time of the models

如圖7所示為不同數據處理模型的運算時間對比，所有模型均從數據輸入后開始計時，至得出預測結果位止。分析可知FsELM模型的運算時間最短，相比SVR縮短了約0.031 s。

5 結 論

抗隨機噪聲干擾能力是評價濾波處理算法能力的重要指標。針對實際應用中的PSD采集信號具有樣本數目有限、受隨機噪聲干擾而引起非線性度強等特點，本文提出一種基于經典ELM的反饋堆疊學習算法，FsELM，通過模型訓練結果與真值的偏差構成反饋，從而構建了多層訓練模型，實現了對數據潛在相關的學習和PSD信號有效信息的高精度提取，預測結果均方誤差為1.4×10-5，相比SVR提高了57%，預測精度為0.78%。FsELM在保持ELM和良好泛化能力的同時，兼具快速學習的優勢，相比其他數據處理算法具有更快的運算速度。