有效長(zhǎng)度系數(shù)的計(jì)算公式研究

田博宇 孫 博 竇艷偉

（中國(guó)石油工程建設(shè)有限公司北京設(shè)計(jì)分公司，北京 100085）

柱或梁柱的設(shè)計(jì)通常都是從柱兩端彈性轉(zhuǎn)動(dòng)阻力（GA，GB）的計(jì)算開(kāi)始，由計(jì)算得到有效長(zhǎng)度系數(shù)K。無(wú)側(cè)移框架體系和有側(cè)移框架體系的數(shù)學(xué)精確方程是由Barakat和Chen提出的，該方法需要大量的計(jì)算來(lái)求解方程，且該方法適用于繁瑣復(fù)雜的柱與梁柱結(jié)構(gòu)體系。

1 精確方程和近似方程的研究背景

考慮一個(gè)兩端彈性約束的柱AB，用GA表示A端的轉(zhuǎn)動(dòng)約束因子，GA表示在A點(diǎn)處連接的所有柱與所有梁的相對(duì)剛度的比值：

在歐洲規(guī)范中，使用了另外兩個(gè)因素βA和βB來(lái)取代GA和GB。β的定義與G的定義不同，公式如下：

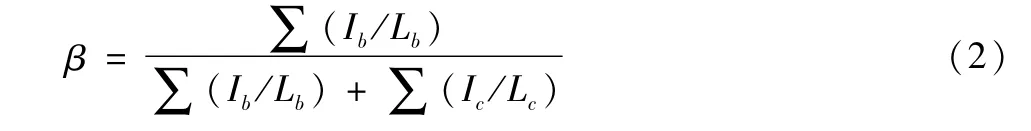
β與G之間的數(shù)學(xué)關(guān)系如下：

歐洲規(guī)范中用β而不用G，當(dāng)連接方式為鉸接時(shí)，取β=0，當(dāng)連接方式為剛接時(shí)，取β=1。

1.1 無(wú)側(cè)移框架體系

無(wú)側(cè)移框架體系是有效防止發(fā)生側(cè)移的框架體系，如圖1中的a，有效長(zhǎng)度系數(shù)K不大于1.0。無(wú)側(cè)移框架柱的計(jì)算長(zhǎng)度系數(shù)表的得出是下述數(shù)學(xué)方程的解的集合：

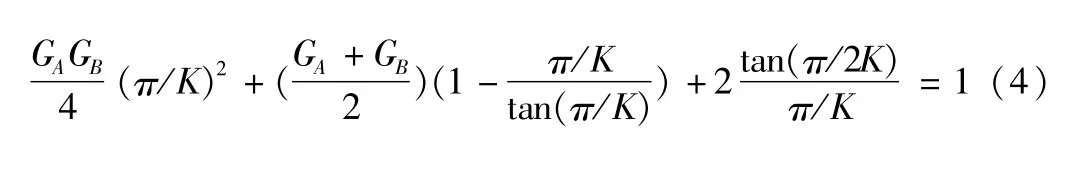
對(duì)于上述方程，只能用數(shù)值方法進(jìn)行求解，法國(guó)規(guī)范中給出的近似解如下：

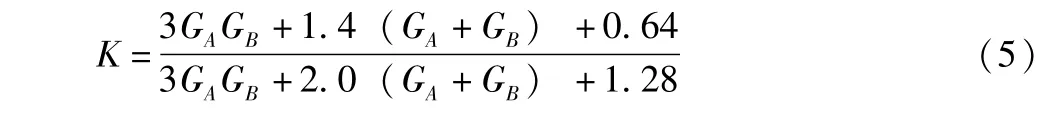
1.2 有側(cè)移框架體系

如果剛性框架僅依靠框架的作用來(lái)抵抗側(cè)向力，則允許其位移的產(chǎn)生，如圖1中的b。在這種情況下，有效長(zhǎng)度系數(shù)K不小于1.0。有側(cè)移框架柱的計(jì)算長(zhǎng)度系數(shù)表的得出是下述數(shù)學(xué)方程的解的集合：

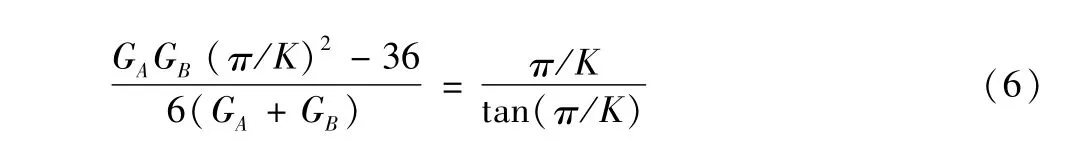
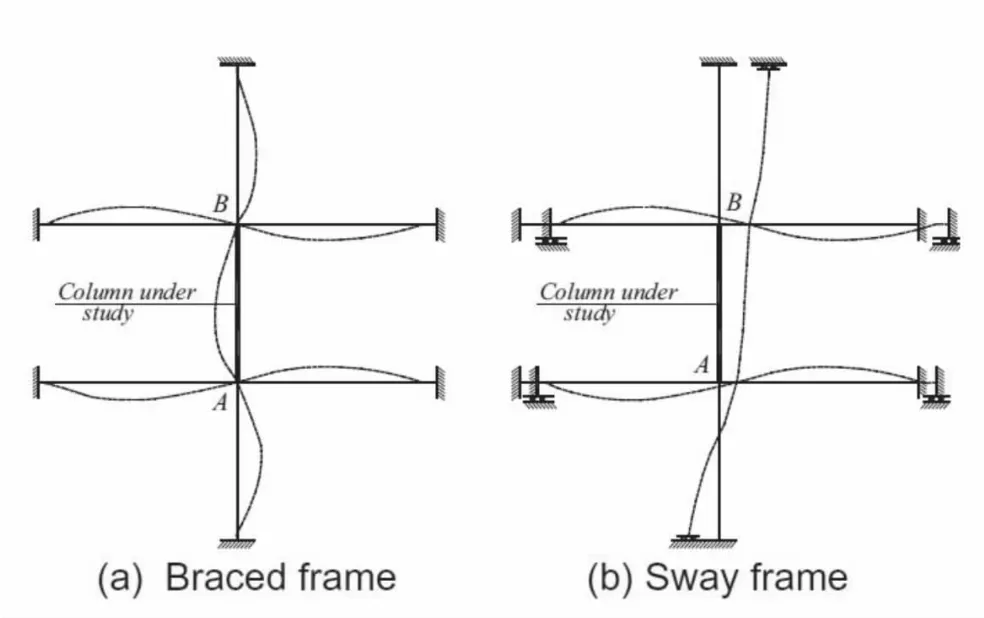
圖1 無(wú)側(cè)移框架體系和有側(cè)移框架體系

上述方程雖然比方程（4）簡(jiǎn)單，但是也同樣不能用封閉形式求解。法國(guó)規(guī)范中建議的近似解形式如下：

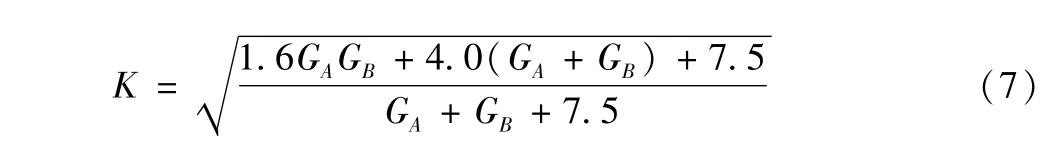
2 理論公式

首先，通過(guò)對(duì)無(wú)側(cè)移框架體系和有側(cè)移框架體系的數(shù)值分析，確定了柱端轉(zhuǎn)動(dòng)阻力（GA，GB）不同實(shí)測(cè)值對(duì)應(yīng)的有效長(zhǎng)度系數(shù)K。將這些三維中的表示有效長(zhǎng)度系數(shù)的點(diǎn)繪制到一個(gè)二維平面中，然后，將這些曲線中系數(shù)K與公式（5）和（7）中的K值對(duì)應(yīng)的解進(jìn)行比較，選擇并進(jìn)行調(diào)整最小標(biāo)準(zhǔn)差得到最佳公式。

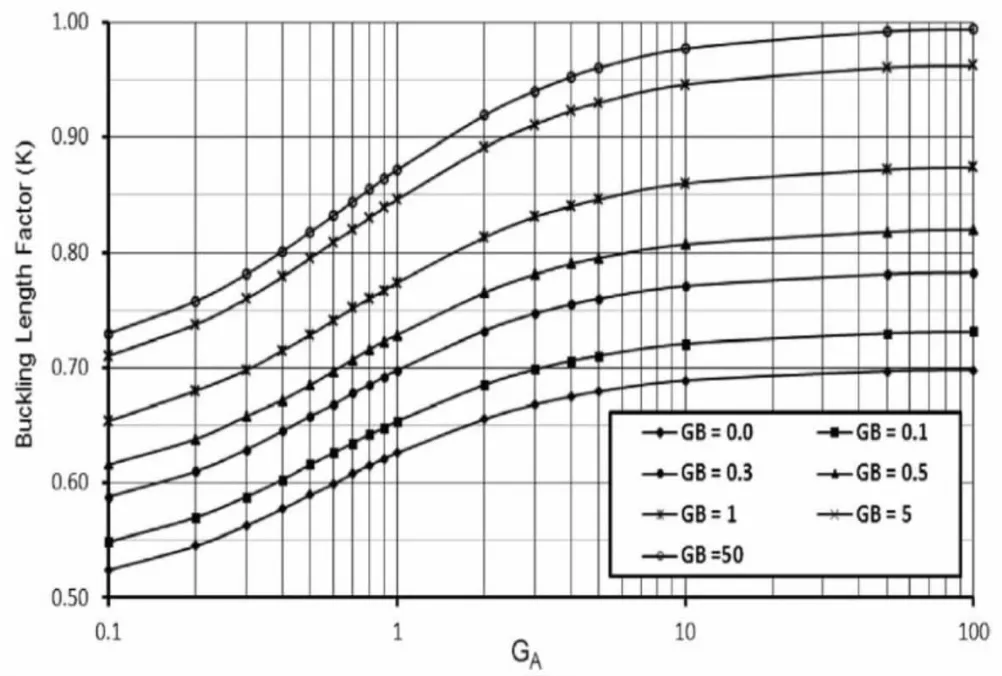
圖2 有效長(zhǎng)度系數(shù)（K）與無(wú)側(cè)移框架體系柱端約束阻力的關(guān)系曲線

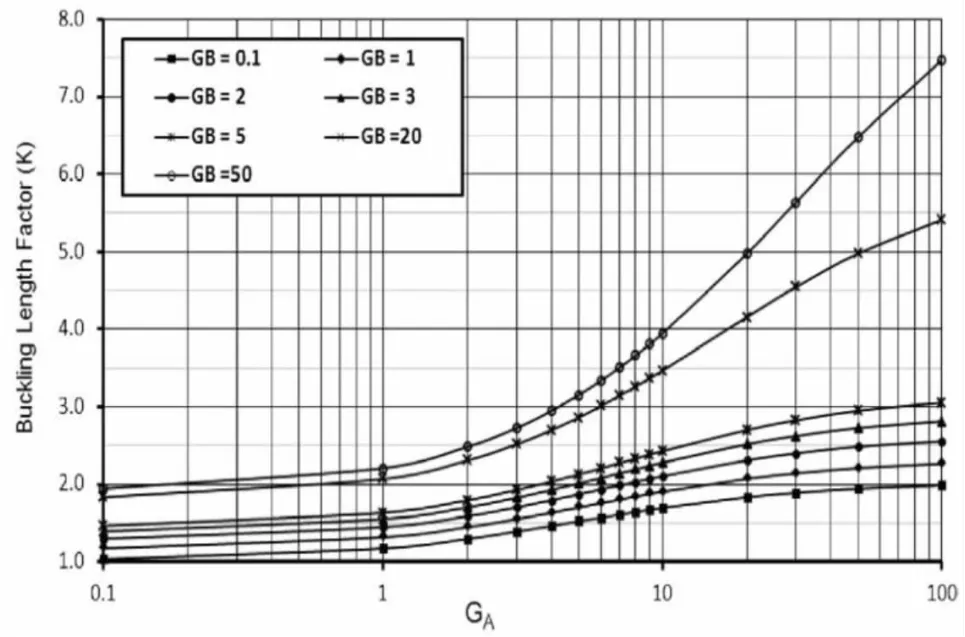
圖3 有效長(zhǎng)度系數(shù)（K）與有側(cè)移框架體系柱端約束阻力的關(guān)系曲線

利用計(jì)算機(jī)軟件對(duì)上述提出的公式進(jìn)行基于最小二乘法的多元回歸分析，可以擬合出標(biāo)準(zhǔn)誤差小且簡(jiǎn)單于法國(guó)規(guī)范中給出的公式。

對(duì)于無(wú)側(cè)移框架體系，得到的有效長(zhǎng)度系數(shù)K的計(jì)算公式如下：

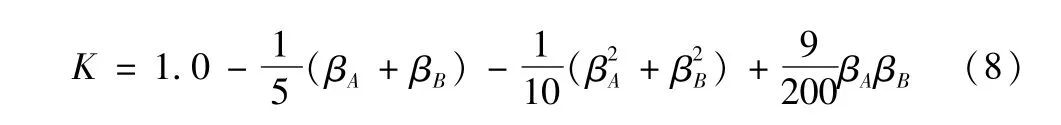
其中：0≤GA≤100，0≤GB≤100

對(duì)于有側(cè)移框架體系，為了得到更為準(zhǔn)確的結(jié)果，根據(jù)柱端轉(zhuǎn)動(dòng)阻力的范圍，得到了有效長(zhǎng)度系數(shù)的兩個(gè)方程如下：

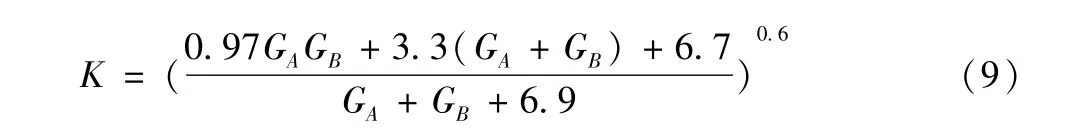
其中：0≤GA≤10，0≤GB≤10

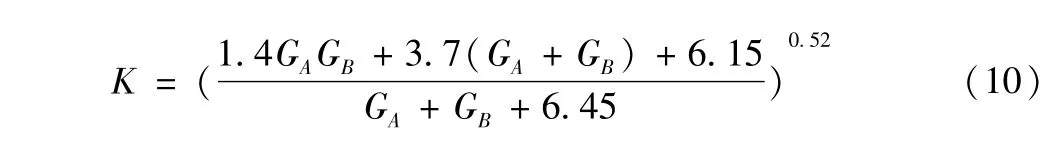
其中：10＜GA≤100或10＜GB≤100

3 精確公式的精確性

我們可以將所得公式給出的結(jié)果與通過(guò)解相應(yīng)的方程得到的結(jié)果進(jìn)行比較，很容易得到相應(yīng)的精確性比較。首先我們可以看一下法國(guó)規(guī)范中關(guān)于有效計(jì)算長(zhǎng)度系數(shù)的圖表和公式，圖表中的精確性主要取決于數(shù)據(jù)量的多少，在數(shù)據(jù)量稍小的圖表中，精度偏差大約為5%；另一方面，法國(guó)規(guī)范中提到無(wú)側(cè)移框架體系中的公式（5）的精度偏差為0.5%，而有側(cè)移框架體系中的公式（7）的精度偏差為1.5%。依據(jù)目前的回歸分析中所有點(diǎn)的誤差百分比（取無(wú)側(cè)移框架體系和有側(cè)移框架體系均為300個(gè)點(diǎn)）表明：本文通過(guò)線性回歸得到的公式對(duì)于無(wú)側(cè)移框架體系公式（8）的精度偏差在0.5%以內(nèi)，對(duì)于有側(cè)移框架體系公式（9）和（10）的精度偏差在1%以內(nèi)。

4 結(jié)果對(duì)比

表1和表2分別表示無(wú)側(cè)移框架體系和有側(cè)移框架體系由公式（8） ～（10）計(jì)算得出的K值與法國(guó)規(guī)范中理論公式（5）和（7）得到的K值結(jié)果進(jìn)行對(duì)比，如下表1和表2：

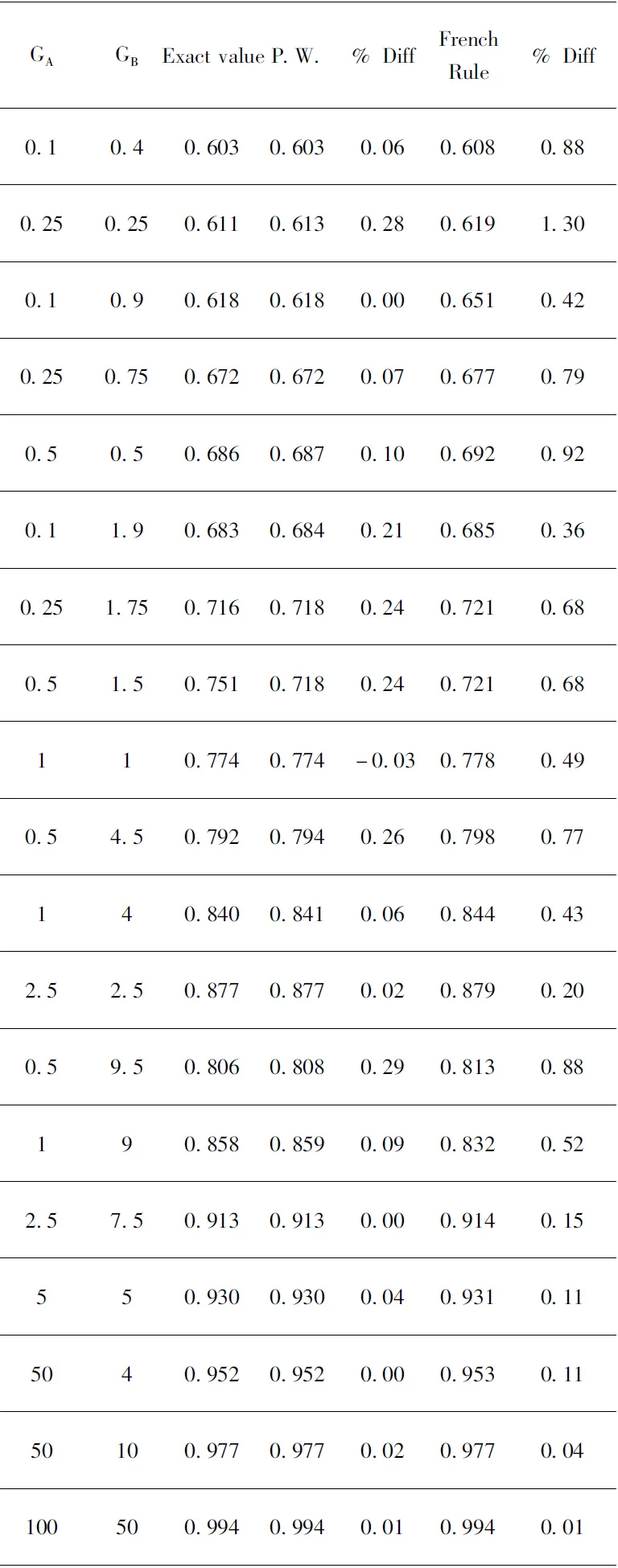
表1 無(wú)側(cè)移框架體系公式（8）K值與公式（5）K值的對(duì)比

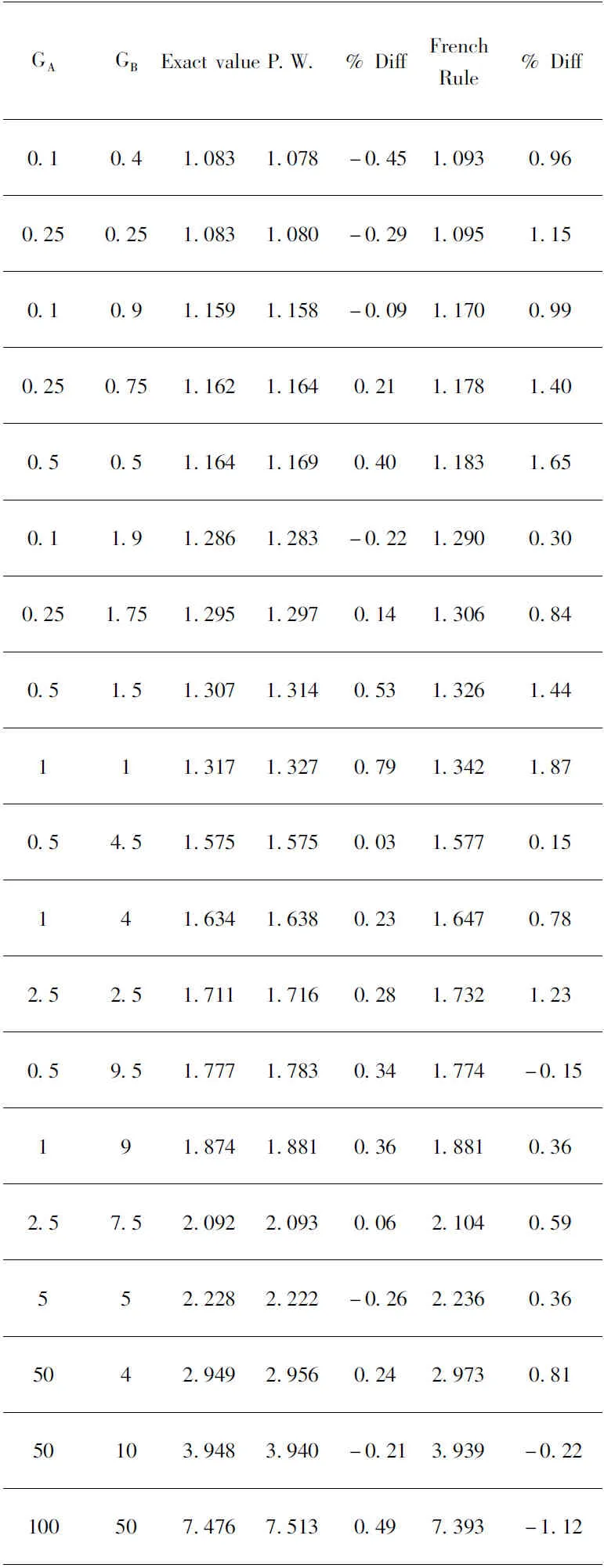
表2 有側(cè)移框架體系公式（9）（10）K值與公式（7）K值的對(duì)比

通過(guò)表1和表2可以清楚看到，雖然公式 （8） ～（10）很簡(jiǎn)單，但是與法國(guó)規(guī)范中的公式（5）和（7）相對(duì)比可以發(fā)現(xiàn)，公式（8） ～（10）的結(jié)果更準(zhǔn)確，更接近于精確值，偏差更小，同樣，精確公式的得出也更方便于工程師日后的計(jì)算工作。

5 結(jié)語(yǔ)

本文通過(guò)對(duì)法國(guó)規(guī)范中有效長(zhǎng)度計(jì)算系數(shù)公式的精確解進(jìn)行多元回歸分析，研究確定了簡(jiǎn)單準(zhǔn)確的鋼結(jié)構(gòu)柱的有效長(zhǎng)度系數(shù)K的計(jì)算公式。其中GA和GB范圍為0～100之間。