一種改進的個體激活因子比例仿射投影算法
楊海斌
(湖南理工職業技術學院,湘潭 411004)
0 引言
當一個系統的脈沖響應系數中有一小部分具有顯著值,而其他系統的系數接近于零時,則該系統被歸類為稀疏系統。對于這樣的系統來說,系統辨識算法是一個具有挑戰性的任務。仿射投影算法在識別稀疏系統時性能較差。在文獻[1]中引入的比例仿射投影算法,通過采用與相應的系數大小成比例的步長調節矩陣來解決這個問題。這種算法盡管在初始階段有很好的收斂速度,但在整個自適應過程期間無法保持這種速度。文獻[2]中引入的改進PAPA算法(MPAPA),使用非線性關系來調整其系數,使所有的系數收斂于最優值的一個界。但MPAPA中激活因子對所有系數都是共有的,并且依賴于自適應濾波器系數向量的瞬時無窮范數,這種計算激活因子的方法導致自適應濾波器系數之間的增益分布不完全符合比例化的概念,其在更新非活動系數時收斂速度會受到影響。為解決此問題,文獻[3]利用個體激活因子替代全局激活因子,提出了IAF-MPAPA算法,其比MPAPA算法提供了更好的增益分配。在IAF-MPAPA算法中,需要對格拉姆矩陣求逆,為了避免計算困難,常用一個稱為正則化因子來對矩陣進行正則化,文獻[4]指出更大的正則化因子導致更小的穩態狀態,但收斂速度較慢。具有固定正則化因子的IAF-MPAPA需要在快速收斂速度和低穩態失調之間進行權衡。針對此問題,文獻[5]通過對IAF-MPAPA的穩態分析,將正則化因子與穩態分析的關系用數學形式表示出來,然后,在進化方法的推動下,提出了具有進化正則化的IAF-MPAPA算法(ERIAF-MPAPA)。但由于ERIAF-MPAPA算法在整個自適應過程中將非活動系數的增益轉換為活動系數的增益,降低了穩態過程中不活躍系數的收斂速度。為此本文提出了一種改進的ERIAF-MPAPA算法(MERIAF-MPAPA),其使用一種新的增益分配策略來更新濾波器系數。該策略在活躍系數接近收斂時增加分配給非活躍系數的增益,且每當學習過程中跨越一個預定義的閾值時,會執行一個新的增益分配,而不是像ERIAF-MPAPA算法那樣將增益與系數大小成正比。新算法使能量在整個學習過程中得到了更好的分配,可以更快的收斂。
1 比例自適應算法
圖1是回聲消除系統的原理框圖,圖中遠端信號x(k)通過回聲信道h產生回聲yˉ(k),近端信號d(k)是由回聲yˉ(k)混和得到。通過使用FIR自適應濾波器w來模擬回聲信道h,可以使所得y(k)逼近回聲信號,進而達到回聲消除的目的。
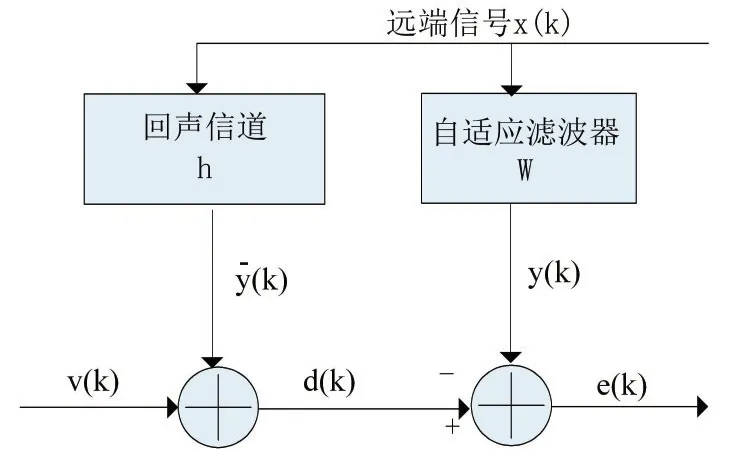
圖1 回聲消除系統
在回聲路徑識別方面,由于脈沖響應時間長且稀疏,NLMS等傳統的自適應算法性能相對較差。PNLMS類型算法通過為每個濾波器數分配步長提高了NLMS算法性能。在PNLMS中,實際回波路徑脈沖響應及其估計和濾波器輸入矢量定義為h=[h1h2…,hN]Tw(k)=[w1(k),w2(k),…,wN(k)]T,x(k)=[x(k)x(k-1),…,x(k-N+1)]T,其中N是自適應濾波器的長度,k是時間指標。并定義d(k)、e(k)表示所需的響應和誤差信號。即:

其中v(k)表示近端噪聲信號。PAPA類型算法是PNLMS類型算法的多維推廣,其通過采用“數據重用”方法對一段數據中的元素進行多次利用改進了PNLMS算法的收斂性能。其輸入X(k)為由P個輸入信號向量組成的矩陣[6]:

P為數據重用因子(又可稱之為投影階數)。并分別記D(k)、E(k)和ε(k)為k時刻的前P個期望輸出、先驗估計誤差和后驗估計誤差所構成的向量,即:
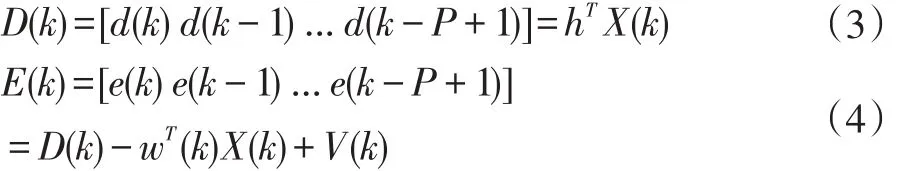
式(3-4)中:

ERIAF-MPAPA算法系數更新過程可表示為:

式中β為步長參數,δn是防止被零整除保證穩定的正則化因子,其計算過程如下:令:
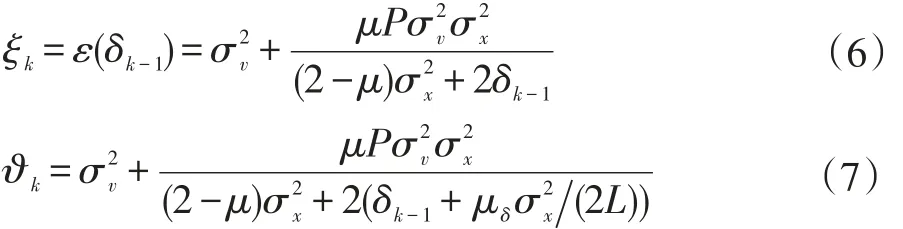
式(5)中Q(k)=diag{q0(k)q1(k)...qL-1(k)}是一個對角矩陣,以更新每個濾波器的估計系數,根據對角元素qi(k)計算式中活化因子fi(k)的區別,PAPA類型算法可分為 IPAPA、MPAPA、IAF-PAPA、ERIAF-MPAPA 等,對于ERIAF-MPAPA,對角元素qi(k)按照如下遞歸關系式進行計算:

式(11)中fi(k)初始值fi(0)=10-4。
2 MERIAF-MPAPA算法
與IPAPA、MPAPA算法相比,ERIAF-MPAPA算法通過fi(k)將部分非活動系數增益轉移到活動系數增益,提供了更好的增益分布使得穩態前的收斂速度和跟蹤能力都得到了很大的提高;但它減緩了穩態階段不活動系數的收斂速度。針對此問題,本文提出一種新的自適應系數增益計算策略。該方法的基本思想是:因對已經達到收斂的自適應系數分配較大的增益實際上對全局收斂沒有影響,所以EIAF-MPAPA算法的比例原理不需要在整個自適應過程中應用。在增益分配的新策略中,目標是當第i個系數達到其最優值wi,opt的鄰近點ε時,重新設計一個新的策略來分配自適應性增益,目標函數定義為[8]:
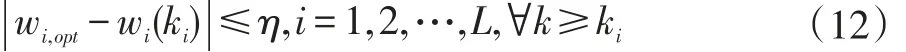
其中wi(ki)是第i個系數的估計值,ki是第i個系數達到最優值所需的迭代次數,η為預定義的閾值。η的范圍可由誤差信號E2(k)的期望值E(E2(k))來確定,E(E2(k))計算如下:

對于MERIAF-MPAPA算法,考慮系數在k次迭代時達到最優值的鄰近點ε,于是有:

假設X(k)和V(k)是不相關的信號,得到:

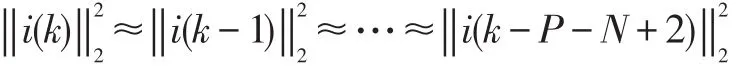
于是,式(15)可寫為:
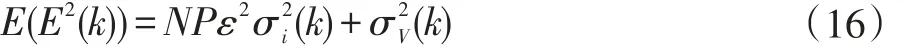
因增益分布的變化必須在達到穩態之前發生,因此η的值必須大于(k)。因此可以用下式來確定η的范圍:
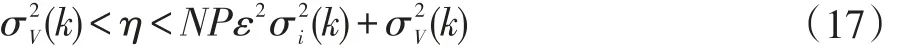
從式(12)可看出,在ki迭代時刻,第i個系數幾乎已經收斂,因此,這個系數不再需要獲得與其幅度成正比的增益。這樣,以前分配給這個系數的部分增益現在可以重新分配給沒有達到最優值鄰近點的系數,從而加快它們的收斂速度。因此,考慮到閾值條件(12),每個系數的單個增益被重寫為:

上式中,對已收斂到最優值的系數,則分配最小增益γi(k)。在式(18)中,我們注意到這種增益分配策略需要事先知道wi,opt的值。但在實際應用中,系數的最優值不是先驗知道的。因此引入如下的瞬時平方誤差的平滑函數ψ(k):
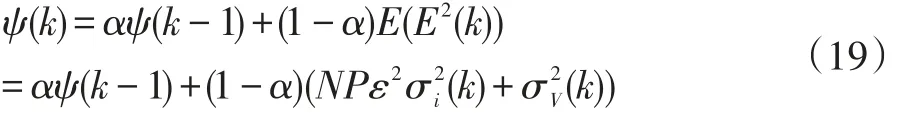
其中0<α<1是平滑因子。因此,在MEIAF-MPAPA算法中,考慮到全局閾值條件,第i個系數的增益表示為:

于是可得增強的MERIAF-MPAPA算法完整遞推公式為:
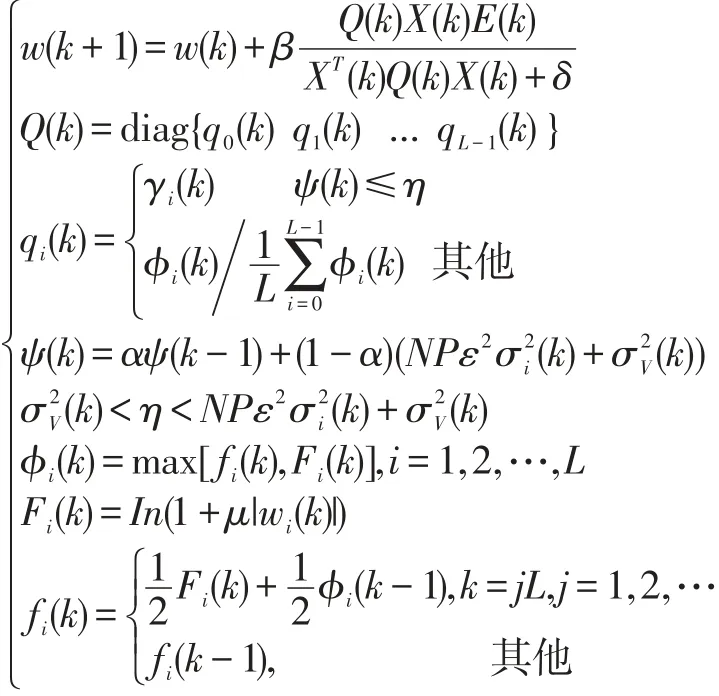
3 仿真分析
為驗證本文算法性能,針對一個高度稀疏的回聲消除系統,通過蒙特卡羅模擬(平均100次獨立運行)比 較 MPAPA、IAF-MPAPA[2014]、ERIAF-MPAPA[2017]和MERIAF-MPAPA算法的性能。四種算法中數據重用因子P=2,為模擬回波路徑脈沖響應,首先定義如下以指數方式衰減的Lu維向量:

其中τ>0是衰變常數。利用方程(21),得到脈沖響應為:

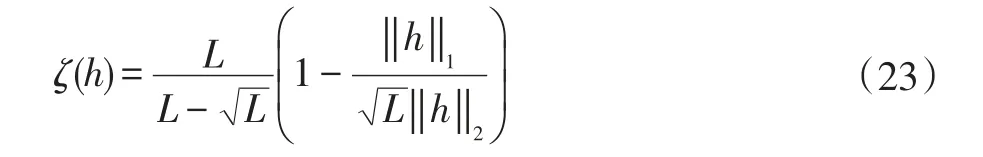
在所有的模擬實驗中,輸入信號是一個相關的、方差為=1的2階零均值自回歸過程,即:
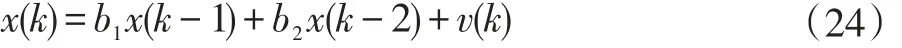
其中b1和b2是過程系數。并采用歸一化失調(misalignment)作為性能比較標準,其定義為:

從圖2可以看出,在所有算法中,本文提出的算法收斂最快。

圖2 算法收斂性能比較
4 結語
本文提出了一種改進的ERIAF-MPAPA算法(MERIAF-MPAPA),該算法在學習過程中使用了一種增益再分配策略,以增加分配給非活動系數的增益,因為活動系數趨于收斂。其次,當達到閾值時,通過對所有自適應系數分配相等的增益來實現這種再分配。仿真結果表明,該算法的收斂速度明顯提高。

