考慮交叉口情況的公交專(zhuān)用道網(wǎng)絡(luò)研究

顧悠揚(yáng)，馬曉旦，夏曉梅，葉靜茹，李辰皓

（1.上海理工大學(xué) 管理學(xué)院，上海 200093；2.上海建科造價(jià)咨詢(xún)有限公司，上海 200000）

1 引言

隨著城市道路擁堵問(wèn)題日益嚴(yán)重，如何提高現(xiàn)有交通網(wǎng)絡(luò)效率已經(jīng)成為交通專(zhuān)業(yè)人員面臨的重要問(wèn)題。雖然已有增加道路建設(shè)、擴(kuò)大路網(wǎng)容量等措施，但現(xiàn)實(shí)發(fā)展表明，僅靠增加道路通行能力無(wú)法應(yīng)對(duì)交通需求的持續(xù)增長(zhǎng)。因此，實(shí)施公交優(yōu)先策略成為建立高效交通系統(tǒng)的新方向[1]。實(shí)施公交優(yōu)先，首先要保證通行權(quán)優(yōu)先。在路網(wǎng)中布設(shè)公交專(zhuān)用道是保證通行權(quán)優(yōu)先的一條有效途徑。20世紀(jì)30年代，公交專(zhuān)用道的概念首次引入；1960年，法國(guó)率先通過(guò)設(shè)置公交專(zhuān)用道的方式來(lái)緩解交通擁堵，并提出“公交優(yōu)先”[2]；1997年，國(guó)內(nèi)第一條公交專(zhuān)用道布設(shè)于北京長(zhǎng)安街。到目前為止，專(zhuān)家和學(xué)者們關(guān)于公交專(zhuān)用道的系統(tǒng)研究越發(fā)深入，可將研究分為微觀(guān)與宏觀(guān)兩部分。

微觀(guān)方面的研究，主要是對(duì)公交專(zhuān)用道的幾何設(shè)計(jì)和相應(yīng)的公交優(yōu)先信號(hào)進(jìn)行了詳細(xì)的討論。在幾何設(shè)計(jì)方面，公交專(zhuān)用道可以是中心公交車(chē)道、偏置公交車(chē)道、路邊公交車(chē)道和反向公交車(chē)道[3]，其設(shè)置通常是因地制宜、相當(dāng)靈活。除了幾何設(shè)計(jì)，適當(dāng)調(diào)整的信號(hào)相位也被認(rèn)為不可缺少。對(duì)于設(shè)置在路段中央的公交專(zhuān)用道，為了避免左轉(zhuǎn)車(chē)輛與專(zhuān)用道上行駛的公交車(chē)輛的沖突，Kim提出了一種協(xié)調(diào)非公交階段與專(zhuān)用公交階段的三環(huán)相位方案，通過(guò)將剩余時(shí)間分配給公交專(zhuān)用道中位數(shù)通道上的非公交階段，提高公交車(chē)輛的平均行駛速度和非公交車(chē)輛的通過(guò)率[4]。而從宏觀(guān)方面來(lái)看，公交專(zhuān)用道的具體布設(shè)是研究重點(diǎn)。SEO等認(rèn)為當(dāng)公交車(chē)流量在20veh/h-400veh/h之間，車(chē)輛流量在1 730veh/h到3 350veh/h之間時(shí)，設(shè)置公交專(zhuān)用道[5]。Horimoto認(rèn)為在主干道上設(shè)置公交專(zhuān)用道需證明其合理性，即當(dāng)存在公交專(zhuān)用道時(shí)的行程時(shí)間小于無(wú)公交專(zhuān)用道的行程時(shí)間時(shí)，可設(shè)置公交專(zhuān)用道[6]。

本文提出以總出行時(shí)間最小為目標(biāo)的模型，模型將車(chē)道分配和信號(hào)相位優(yōu)化結(jié)合為一體，以此選擇最合適的公交專(zhuān)用道網(wǎng)絡(luò)設(shè)計(jì)。

2 公交專(zhuān)用道網(wǎng)絡(luò)優(yōu)化

公交專(zhuān)用道的網(wǎng)絡(luò)優(yōu)化問(wèn)題是城市交通網(wǎng)絡(luò)設(shè)計(jì)問(wèn)題。隨著數(shù)學(xué)設(shè)計(jì)和網(wǎng)絡(luò)設(shè)計(jì)問(wèn)題的發(fā)展，雙層規(guī)劃模型出現(xiàn)在大眾視野，上層優(yōu)化網(wǎng)絡(luò)，下層從出行者的角度描述。Mesbah等提出了雙層規(guī)劃模型，以系統(tǒng)總出行時(shí)間為上層優(yōu)化目標(biāo)，下層為靜態(tài)交通流量分配模型，求解公交專(zhuān)用道的最優(yōu)布設(shè)[7]。Miandoabchi等提出了一個(gè)多目標(biāo)雙峰城市交通網(wǎng)絡(luò)設(shè)計(jì)問(wèn)題，包括小汽車(chē)和公交車(chē)模型以及道路網(wǎng)絡(luò)和公交網(wǎng)絡(luò)的同時(shí)設(shè)計(jì)，并考慮了兩種模式的流量對(duì)彼此的影響[8]。針對(duì)公交專(zhuān)用道對(duì)路網(wǎng)運(yùn)行效率的影響，考慮模型選擇與公交專(zhuān)用道分配的相關(guān)性，Abdelghany等提出了一種動(dòng)態(tài)交通分配和仿真模型，用于評(píng)估BRT不同運(yùn)行特性對(duì)客運(yùn)量和交通流的潛在影響[9]。Uchida等探討了一個(gè)考慮出行者行為的網(wǎng)絡(luò)設(shè)計(jì)問(wèn)題，該問(wèn)題由基于概率的多式聯(lián)運(yùn)分配模型表示，同時(shí)考慮了鐵路、公交和小汽車(chē)三種交通方式，以及小汽車(chē)和公交車(chē)過(guò)飽和的相互作用[10]。

研究表明，公交專(zhuān)用道有助于改善路網(wǎng)運(yùn)營(yíng)狀況，但無(wú)限制增加公交專(zhuān)用道并不可行。目前的公交專(zhuān)用道網(wǎng)絡(luò)優(yōu)化研究主要集中于專(zhuān)用道對(duì)路網(wǎng)整體的作用，而忽略了專(zhuān)用道在交叉口產(chǎn)生的影響。事實(shí)上，大多數(shù)交通延誤都發(fā)生在交叉口。由于公交專(zhuān)用道的設(shè)置，其他車(chē)道在交叉口的減少可能導(dǎo)致綠燈時(shí)間的調(diào)整。因此，不僅相應(yīng)路段上的車(chē)輛行駛會(huì)受到影響，相鄰路段也會(huì)受到影響。忽略這種影響可能會(huì)低估公交專(zhuān)用道對(duì)網(wǎng)絡(luò)的負(fù)面影響，導(dǎo)致網(wǎng)絡(luò)優(yōu)化設(shè)計(jì)結(jié)果不理想。

為了克服這一不足，本文提出的優(yōu)化模型是通過(guò)選擇最合適的公交專(zhuān)用道網(wǎng)絡(luò)設(shè)計(jì)來(lái)減少總出行時(shí)間，即以系統(tǒng)出行時(shí)間最小為目標(biāo)，將交叉口處的車(chē)道重新分配和信號(hào)相位優(yōu)化集成在一個(gè)框架內(nèi)。

3 模型建立

公交專(zhuān)用道的優(yōu)化設(shè)計(jì)問(wèn)題是一個(gè)復(fù)雜的決策問(wèn)題，需要在路網(wǎng)系統(tǒng)中綜合權(quán)衡決策者及出行者雙方的利益。其中，決策者是關(guān)于公交專(zhuān)用道優(yōu)化設(shè)計(jì)的決策部門(mén)，權(quán)衡的是整個(gè)網(wǎng)絡(luò)系統(tǒng)的效益；而出行者更加關(guān)注的是自身的實(shí)際出行時(shí)間。因此采用雙層規(guī)劃模型。上層模型從系統(tǒng)角度出發(fā)，決定哪條路段上建設(shè)專(zhuān)用道、交叉口處公交專(zhuān)用道的設(shè)置以及形式為路中型還是路側(cè)型，建立上層模型的目標(biāo)函數(shù)，其優(yōu)化結(jié)果保證整個(gè)路網(wǎng)系統(tǒng)的總出行時(shí)間最短；下層模型從小汽車(chē)和公交車(chē)兩個(gè)角度來(lái)建立模型，在由上層模型確定出的包含鋪設(shè)公交專(zhuān)用道的基礎(chǔ)，出行者選擇相應(yīng)的出行路徑來(lái)實(shí)現(xiàn)出行時(shí)間最少。

3.1 上層模型

上層模型以總出行時(shí)間最小為目標(biāo)來(lái)建立目標(biāo)函數(shù)，并給出了相應(yīng)的約束條件，具體如下：

式中，VaC是路段a上的小汽車(chē)流量（人/h）；taC是路段a上的小汽車(chē)的阻抗函數(shù)（min）；VaB是路段a上的公交車(chē)流量（人/h）；taB是路段a上的公交車(chē)的阻抗函數(shù)（min）；Vriw是交叉口r上岔口i流向w的流量（人/h）；triw是交叉口r上岔口i流向w的阻抗函數(shù)（min）。

（1）路段車(chē)道功能劃分約束條件。雙向各功能車(chē)道數(shù)（公交專(zhuān)用道與社會(huì)車(chē)道）之和應(yīng)與路段總車(chē)道數(shù)相等；同時(shí)，雙向至少應(yīng)有一條社會(huì)車(chē)道。

（2）交叉口車(chē)道功能約束條件。交叉口屬于比較復(fù)雜的部分，約束條件也比路段更加多，在此引入進(jìn)口和出口的概念。主要約束條件如下：進(jìn)口車(chē)道數(shù)與各功能車(chē)道的車(chē)道數(shù)之和相等。進(jìn)口車(chē)道數(shù)與出口車(chē)道數(shù)之和等于岔口總車(chē)道數(shù)之和，且進(jìn)口與出口車(chē)道數(shù)之和不小于路段車(chē)道數(shù)；為了讓社會(huì)車(chē)輛有車(chē)道可以行駛，因此進(jìn)口道和出口道的社會(huì)車(chē)輛的車(chē)道數(shù)應(yīng)不小于1。本文設(shè)定十字形交叉口，岔口i=4。

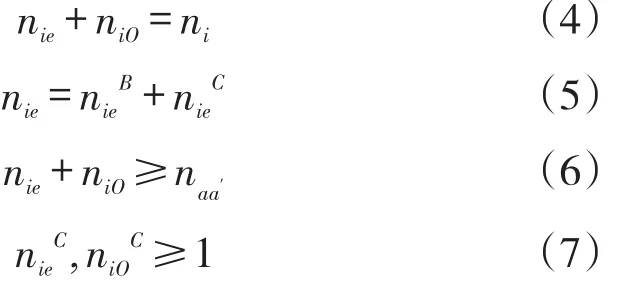
式中，nie是岔口i的進(jìn)口車(chē)道數(shù)（條）；niO是岔口i的出口車(chē)道數(shù)（條）；是岔口i進(jìn)口的公交車(chē)道數(shù)（條）；是岔口i進(jìn)口的小汽車(chē)的車(chē)道數(shù)（條）；ni是岔口i的總車(chē)道數(shù)（條）；是岔口i出口的小汽車(chē)的車(chē)道數(shù)（條）。

（3）公交專(zhuān)用道幾何設(shè)置約束條件。交叉口處公交專(zhuān)用道應(yīng)與路段一致。若路段公交專(zhuān)用道設(shè)置為路外側(cè)型，則交叉口處的設(shè)置形式也是路外側(cè)型。

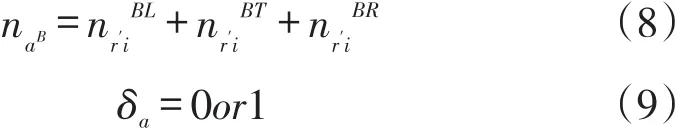
式中，naB是在路段處公交車(chē)的車(chē)道數(shù)（條）；是交叉口在岔口i處公交車(chē)左轉(zhuǎn)的車(chē)道數(shù)（條）；T是交叉口在岔口i處公交車(chē)直行的車(chē)道數(shù)（條）；是交叉口在岔口i處公交車(chē)右轉(zhuǎn)的車(chē)道數(shù)（條）；δa是公交專(zhuān)用道的形式，δa=0表示路中型，δa=1表示路側(cè)型。

（4）交叉口信號(hào)控制。采用雙環(huán)相位設(shè)計(jì)進(jìn)行信號(hào)配時(shí)，圖1給出了雙環(huán)八相位的具體方向。

圖1 雙環(huán)八相位具體方向

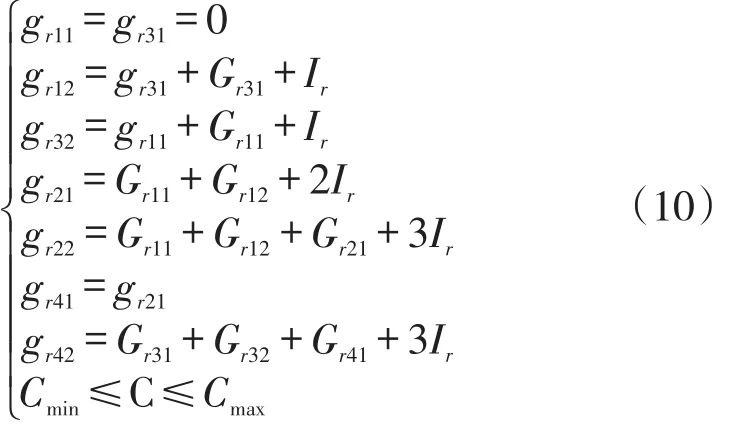
式中，griw是流向w的綠燈開(kāi)始時(shí)刻（s），其中w=1為左轉(zhuǎn)，w=2為直行，w=3為右轉(zhuǎn)；i=1,2,3,4分別為四個(gè)方向的岔口；Griw是流向w的綠燈時(shí)長(zhǎng)（s）；Ir是交叉口 r的綠燈間隔時(shí)間（s）；C 是交叉口信號(hào)周期時(shí)長(zhǎng)（s）。

（5）出行時(shí)間（阻抗）計(jì)算。本文采用BPR函數(shù)作為路段阻抗函數(shù)和交叉口阻抗函數(shù)，兩者區(qū)別在于所取得參考系數(shù)不同。路段小汽車(chē)的阻抗函數(shù)記為taC，公交車(chē)的阻抗函數(shù)記為taB；交叉口阻抗函數(shù)記為triw。

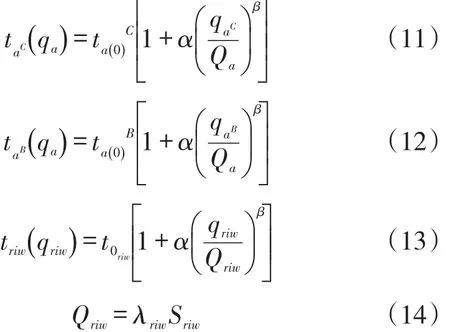
式中，qriw是交叉口r岔口i處w流向的流量（人/h）；Qriw是交叉口r岔口i處w流向的通行能力（人/h）；λriw是交叉口r岔口i處w流向的綠信比；是交叉口r岔口i處w流向的飽和流量是0流量時(shí)在交叉口r岔口i處w流向的行駛時(shí)間（min）；α，β是模型參數(shù)。

3.2 下層模型

下層分配模型采用隨機(jī)用戶(hù)均衡，分別對(duì)小汽車(chē)和公交車(chē)進(jìn)行車(chē)流分配，即分為2個(gè)子模型，小汽車(chē)流量分配模型和公交車(chē)流量分配模型。

（1）小汽車(chē)流量分配模型。以廣義出行時(shí)間最小為目標(biāo)函數(shù)，以O(shè)D對(duì)及路段層次的流量守恒限制、容量限制及為保證路徑流量為非負(fù)的可行解作為模型約束條件，公式如下：

式中，ZC是小汽車(chē)網(wǎng)絡(luò)廣義出行費(fèi)用（min）；AC是小汽車(chē)網(wǎng)絡(luò)所有小汽車(chē)路段aC的集合；vaC是小汽車(chē)路段aC的乘客數(shù)（人）；taC是小汽車(chē)路段aC阻抗，即小汽車(chē)出行廣義費(fèi)用（min）；是乘客對(duì)小汽車(chē)網(wǎng)絡(luò)熟悉度的量度，值越大表示對(duì)網(wǎng)絡(luò)越熟悉，當(dāng)θC→∞時(shí)，模型轉(zhuǎn)換為用戶(hù)平衡模型；為小汽車(chē)OD對(duì)的集合；是小汽車(chē)OD對(duì)之間所有的可行路徑；fC是小汽車(chē)路徑是路徑上的流量是流量為時(shí)小汽車(chē)在路段a上的行程時(shí)間是零流量時(shí)小汽車(chē)在路段a上的行程時(shí)間（min）；Qa是路段a的可能通行能力（人/h）；α，β是模型參數(shù)是OD對(duì)之間的小汽車(chē)需求（人/h）；paCfC是0-1標(biāo)記變量，若為1則表示路段aC在路徑上，否則表示不在是路段aC的容量。

（2）公交車(chē)流分配模型。采用最優(yōu)出行策略的分配方法對(duì)已知的公交流量進(jìn)行路徑分配，從而實(shí)現(xiàn)公交出行者的總出行時(shí)間最短。公式如下：

式中，Z2是公交網(wǎng)絡(luò)廣義出行費(fèi)用（人/min）；m是公交網(wǎng)絡(luò)中的節(jié)點(diǎn)；M是公交網(wǎng)絡(luò)的節(jié)點(diǎn)集；A+m是進(jìn)入節(jié)點(diǎn)m的線(xiàn)路集合；是離開(kāi)節(jié)點(diǎn)m的線(xiàn)路集合；fa是路段a上通過(guò)的所有公交線(xiàn)路頻率之和；ωa是0-1變量，表示路段a是否屬于集合；gm是節(jié)點(diǎn)m上產(chǎn)生的客流量；是流量為時(shí)公交在路段a上的行程時(shí)間（人/min）是零流量時(shí)公交在路段a上的行程時(shí)間（人/min）；Qa是路段a的可能通行能力（人/h）；Vm是節(jié)點(diǎn)m上的客流量；α，β是模型參數(shù)。

3.3 模型求解

在模型求解方面，由于遺傳算法同時(shí)具備隨機(jī)性、自適應(yīng)性、收斂性及與其它算法的兼容性等特性，適合求解網(wǎng)絡(luò)優(yōu)化問(wèn)題，本文采用遺傳算法求解上層模型，得到公交專(zhuān)用道的布局。下層模型則通過(guò)交通規(guī)劃軟件EMME中的公交分配模塊及小汽車(chē)分配模塊實(shí)現(xiàn)。

遺傳算法具體步驟如下：

步驟1：設(shè)置進(jìn)化代數(shù)計(jì)數(shù)器t=0，設(shè)置最大進(jìn)化數(shù)T，隨機(jī)生成M個(gè)個(gè)體作為初始群體P(0)。

步驟2：計(jì)算群體P(t)中每個(gè)個(gè)體的適應(yīng)度。

步驟3：將選擇算子作用于群體。選擇的目的是把優(yōu)化的個(gè)體直接遺傳到下一代或通過(guò)配對(duì)交叉產(chǎn)生新的個(gè)體再遺傳到下一代。選擇操作是建立在群體中個(gè)體的適應(yīng)度評(píng)估基礎(chǔ)上的。

步驟4：將交叉算子作用于群體。

步驟5：將變異算子作用于群體。即是對(duì)群體中的個(gè)體串的某些基因座上的基因值作變動(dòng)。群體P(t)經(jīng)過(guò)選擇、交叉、變異運(yùn)算后得到下一代群體P(t+1)。

步驟6：若t=T,則輸出最優(yōu)解，終止計(jì)算。

通過(guò)上層得到的專(zhuān)用道優(yōu)化布局，下層利用交通規(guī)劃軟件EMME來(lái)解決網(wǎng)絡(luò)流量分配問(wèn)題。在EMME中，通過(guò)模式選擇將公交專(zhuān)用道和其他車(chē)道設(shè)置為不同的路段，以此區(qū)分通行車(chē)輛的種類(lèi)。因此，交叉口所有可能出現(xiàn)的交通流，最初應(yīng)該由16個(gè)節(jié)點(diǎn)和40個(gè)鏈路來(lái)表示，經(jīng)過(guò)道路簡(jiǎn)化后，改為使用16個(gè)節(jié)點(diǎn)和24條鏈路，相比之下減少了40%的鏈路。

4 驗(yàn)證與分析

4.1 路網(wǎng)參數(shù)標(biāo)定

路網(wǎng)有3條公交線(xiàn)路，3個(gè)十字交叉口。公交線(xiàn)路1和2的需求量都為30pcu/h，公交線(xiàn)路3的需求量為10pcu/h。小汽車(chē)的OD對(duì)（4，8）、（8，4）、（3，11）、（11，3）交通需求量為200pcu/h，其余的OD對(duì)的交通需求量為50pcu/h。設(shè)定迭代長(zhǎng)度為120s；任何一對(duì)相沖突的岔口的時(shí)間間隔設(shè)定值為4s；在交叉點(diǎn)處的所有車(chē)道的飽和流量均設(shè)置為1 800pcu/h；在路段與岔口處的自由流行程時(shí)間分別為10s和20s；公交車(chē)的乘客數(shù)設(shè)定為50人/輛，小汽車(chē)的乘客數(shù)設(shè)定為2人/輛；在BPR函數(shù)中，路段上的α取值為1.5，β取值為2；岔口上的α取值為2，β取值為3。

4.2 驗(yàn)證分析

為了更好地說(shuō)明情況，本文選取東西向路段的公交專(zhuān)用道全部為路外側(cè)型。為了論證交叉口對(duì)路網(wǎng)的影響，根據(jù)模型可將公交專(zhuān)用道的布局設(shè)置為三種進(jìn)行對(duì)比分析，分為考慮交叉口和不考慮交叉口情形下進(jìn)行，如圖2-圖4所示。

圖2、圖3、圖4分別對(duì)應(yīng)方案一、方案二、方案三，對(duì)比結(jié)果見(jiàn)表1。

圖2 路網(wǎng)示意圖

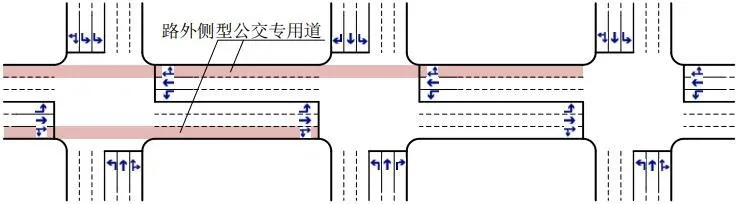
圖3 考慮交叉口的公交專(zhuān)用道優(yōu)化布局

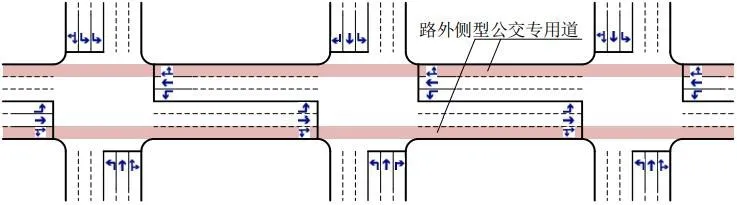
圖4 不考慮交叉口的公交專(zhuān)用道優(yōu)化布局

表1 兩種情形下的乘客總出行時(shí)間（h）

由表1可知，在考慮交叉口的情形下，方案二是最佳方案；而在不考慮交叉口的情形下，方案三是最佳方案。相比之下可以看出，若忽略交叉口，會(huì)造成錯(cuò)選最優(yōu)方案；而考慮交叉口情形下的出行時(shí)間總體遠(yuǎn)大于不考慮交叉口的情形，證明了交叉口是造成延誤的重要因素。

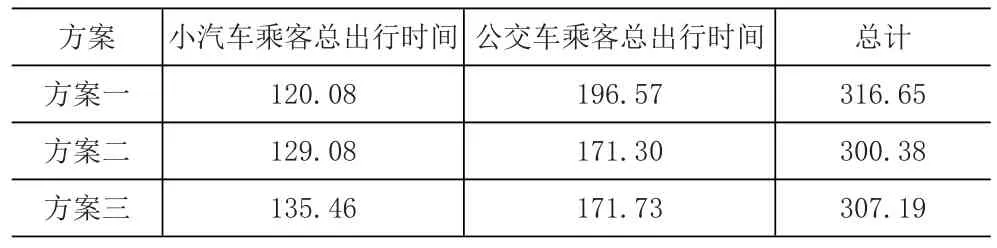
表2 當(dāng)公交線(xiàn)路3的交通量為30pcu/h的對(duì)比

表2是為了論證公交專(zhuān)用道設(shè)置是否越多越好，將公交線(xiàn)路3的公交車(chē)的需求量增加至30pcu/h。由結(jié)果可知，方案二的總出行時(shí)間最少，是最佳方案。對(duì)比公交車(chē)乘客總出行時(shí)間，方案二略低于方案三，這表明公交專(zhuān)用道設(shè)置增多的情況下，隨著路網(wǎng)中公交車(chē)的交通量增加，公交車(chē)出行時(shí)間差距并不大；將小汽車(chē)總出行時(shí)間進(jìn)行比較，可以看出方案三的總出行時(shí)間最大。因此，當(dāng)路網(wǎng)中公交車(chē)流量增加時(shí)，過(guò)多設(shè)置公交專(zhuān)用道會(huì)占用原有車(chē)道，造成小汽車(chē)延誤增加，交叉口的通行效率降低，即使公交車(chē)在路段行駛時(shí)間減少但在交叉口的行駛時(shí)間可能反而增加。

5 結(jié)語(yǔ)

本文為減少總出行時(shí)間，提出了公交專(zhuān)用道網(wǎng)絡(luò)設(shè)計(jì)的雙層優(yōu)化模型。基于建立的雙層規(guī)劃模型，提出采用遺傳算法求解上層模型，下層采用EMME軟件中的公交分配模型及小汽車(chē)分配模型進(jìn)行求解。對(duì)模型進(jìn)行驗(yàn)證，通過(guò)不同方案的比較，得出以下結(jié)論：

（1）本文基于網(wǎng)絡(luò)優(yōu)化，提出了基于系統(tǒng)最優(yōu)與出行者最優(yōu)的雙層規(guī)劃模型，將系統(tǒng)人均總出行時(shí)間最少作為上層模型的目標(biāo)函數(shù)，并給出相關(guān)的約束條件；在下層模型中，以人均總出行時(shí)間最少為目標(biāo)，采用隨機(jī)配流分配模型，包括公交車(chē)及小汽車(chē)的分配模型。該模型考慮了公交專(zhuān)用道與公交車(chē)輛在交叉口的相互作用，優(yōu)化了公交專(zhuān)用道的布局，避免產(chǎn)生錯(cuò)選最優(yōu)方案的后果；

（2）實(shí)驗(yàn)證明，本文建立的模型減少了所有乘客的總出行時(shí)間和小汽車(chē)乘客的出行時(shí)間。這表明，公交專(zhuān)用道設(shè)置的不合理可能會(huì)對(duì)小汽車(chē)出行造成負(fù)面影響。