求解無約束優(yōu)化問題的非單調(diào)自適應(yīng)信賴域方法

徐明明

（成都理工大學(xué)，四川 成都610059）

1 概述

傳統(tǒng)的求解無約束優(yōu)化問題的迭代方法是行搜索方法或信賴域方法。很多學(xué)者通過改進信賴域半徑以及非單調(diào)項來提高信賴域方法的魯棒性以及加快收斂速度。

2 問題的提出

考慮無約束優(yōu)化問題：

在傳統(tǒng)信賴域方法中，通過解決以下子問題，選擇一個試驗步驟dk：

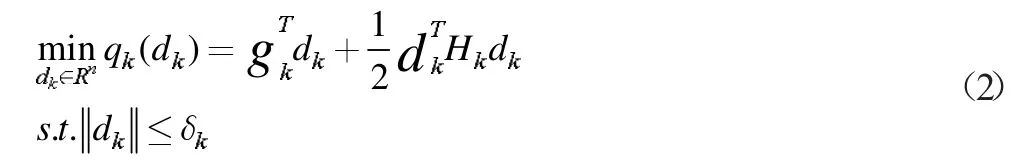
其中g(shù)k∈Rn和Hk∈Rn分別是在當(dāng)前迭代點xk處f（x）的梯度和Hessian 矩陣的近似。||·||是歐氏范數(shù)，δk>0 是當(dāng)前迭代點的信賴域半徑。

3 新的非單調(diào)自適應(yīng)信賴域方法

在這一部分中，提出了一種新的非單調(diào)自適應(yīng)信賴域算法，該算法是基于文獻[1]中提出的非球面信賴域半徑與文獻[2]中提出的一種新的非單調(diào)比率。

在文獻[1]中，作者提出了一種非球面信賴域的非單調(diào)信賴域算法。

首先，介紹了一種基于Hessian 矩陣在當(dāng)前迭代點的特征值，然后將非單調(diào)搜索策略與信任區(qū)域方法相結(jié)合。其算法如下：

將λki設(shè)置為在迭代點xk處Hessian 矩陣Hk的第i 個特征值。通過Ger觢gorin Circle theorem，得到：

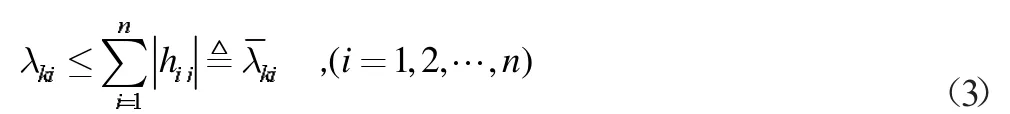
然后，在迭代點xk處的第i 維中的非球面信賴域的尺度可以由

確定。也就是說，試驗步驟dk在（2）中的第i 個元素dki在[-δki，δki]中是有界的。

利用（4），可以將球面信賴域轉(zhuǎn)換為非球面信賴域。因此，子問題（2）轉(zhuǎn)換為

為了進一步調(diào)整信賴域，引入了以下兩個參數(shù)：

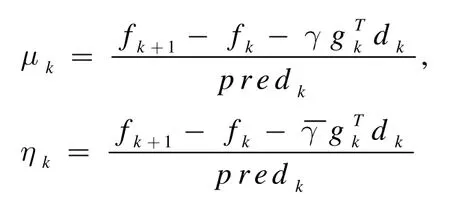
為了提高信賴域算法的計算效率以及增強收斂性，文獻[2]提出來一種新的非單調(diào)項：

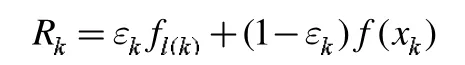
其中

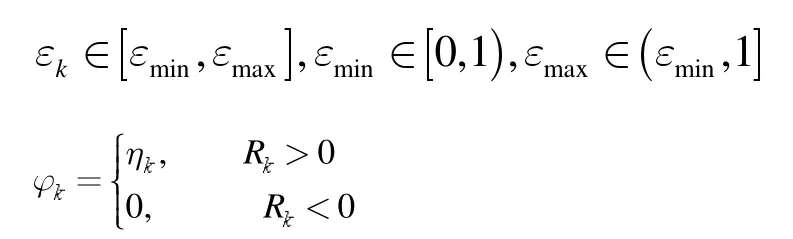
其中是滿足下列條件的正序列：

信賴域比率如下：

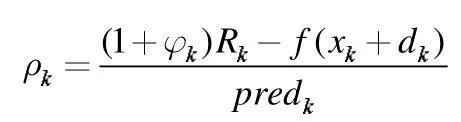
基于以上兩種方法，本文提出了新的信賴域算法：

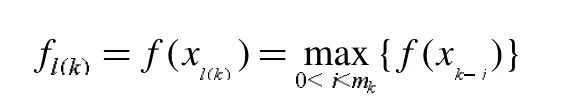
Step3：在迭代點xk處求解子問題（5）。

Step4：計算fk+1，通過（4）計算δki，

Step6：令xk+1=xk+dk，mk=min{k，M}，k：=k+1 轉(zhuǎn)Step2。

4 結(jié)論

本文提出的新的非單調(diào)自適應(yīng)信賴域算法，是文獻[1]與文獻[2]的優(yōu)點的一個融合。以后，會對本算法進行進一步的研究。