空間碎片繩網捕獲拖曳恒張力控制

盧 山，姜澤華，劉 禹

(1. 上海航天控制技術研究所，上海 201109；2. 上海市空間智能控制技術重點實驗室，上海 201109)

0 引 言

目前在軌運行的航天器已達數千顆，預計10年內每年超過服役期的航天器將達到百顆以上。其中低軌失效航天器自然衰減至大氣層燒毀將需要幾十年甚至更長的時間，靜止軌道航天器若在壽命末期不采取措施則會永久滯留于駐泊點，使得可安全利用的軌道資源，特別是靜止軌道駐泊點進一步減少。據NASA(National Aeronautics and Space Administr-ation, NASA)最新數據顯示，截止2019年6月27日已監測到19677個大型在軌運行目標，其中包括5163個有效載荷和14514個火箭箭體，而直徑大于1 cm的碎片總數估計在百萬量級，主要集中分布于高度在2000 km以下的近地軌道和地球同步軌道。NASA科學家Kessler等[1]在1978年就已指出，空間碎片之間的碰撞會產生更多的碎片，從而極大地增加潛在的碎片碰撞概率，并由此導致碎片數量呈指數級增長。事實上，2009年2月10日發生的美國銥星33與俄羅斯宇宙號2251的衛星碰撞事件表明，空間碎片的碰撞連鎖反應已被經觸發了[2]。在2007年，NASA空間碎片計劃負責人Johnson[3]指出自2020 年起，每年清除5～20個大型空間碎片就可抑制空間碎片總量的增長，從而保證未來空間環境不再持續惡化。至此，空間碎片主動清除被提上了各國空間技術的發展日程。空間碎片主動清除方式主要有電動力繩索降軌、機械臂抓捕、繩網捕獲拖曳、太陽帆增阻和激光照射等。其中，繩網捕獲拖曳概念因其重量輕、靈活性高和控制簡單等優點，成為近幾年最受學者關注的碎片清除技術之一。

近些年來，針對繩系拖曳系統控制方法研究，各國學者已經做了一些理論研究工作。文獻[4]研究了通過系繩連接的空間碎片與空間拖船組合體的動力學問題，結果表明，若空間拖船推力的方向與系繩方向一致，且系繩保持張緊，那么離軌過程就是安全的。文獻[5-6]針對空間拖船和廢棄星的繩系組合體，考慮了廢棄星上的撓性部件，如帆板的影響，提出了一種推力控制策略以避免碰撞。文獻[7]提出了一種包含加速、平衡、旋轉和返回的4階段繩系組合體離軌方案，并進行了仿真分析，為工程實現提供了技術思路。文獻[8-9]主要針對拖曳過程中組合體的擺動問題，分別設計了分層滑模控制器及高階滑模控制器。文獻[10]考慮到利用系繩拉力進行姿態控制時，系繩拉力波動對姿態的影響，采用了魯棒性較強的滑模變結構控制方法進行協調控制器的設計。文獻[11]分析了軌道轉移過程中面內外擺角的擺振特性，采用線性二次型調節器(Linear Quadratic Regulator, LQR)設計了系繩張力控制律以抑制擺角振動，實現繩系衛星系統的穩定。

上述研究提出在空間繩系組合體拖曳離軌任務中采用各種時變張力控制律，仿真結果表明系統響應速度快，控制精度高。然而，采用時變張力控制律控制碎片拖曳，對測量設備的測量精度和執行機構的響應速度等性能提出了極高的要求，目前難以在工程中應用。考慮工程實現可行性，使用現有技術設備即可滿足性能要求，本文提出采用恒定張力拖曳被繩網捕獲的碎片目標的控制方法，通過理論推導證明僅采用恒定張力即可實現拖曳過程的穩定控制，并分別針對空間碎片可能產生的姿態章動及繩系組合體的出現的面內外擺動設計控制律。

1 空間繩系組合體動力學建模

1.1 系統組成

典型的繩系拖曳系統由拖船航天器、空間碎片和系繩組成，拖船航天器與空間碎片通過系繩連接。本文針對失效航天器演化成的大型空間碎片目標，利用牛頓歐拉法建立繩系組合體動力學模型。

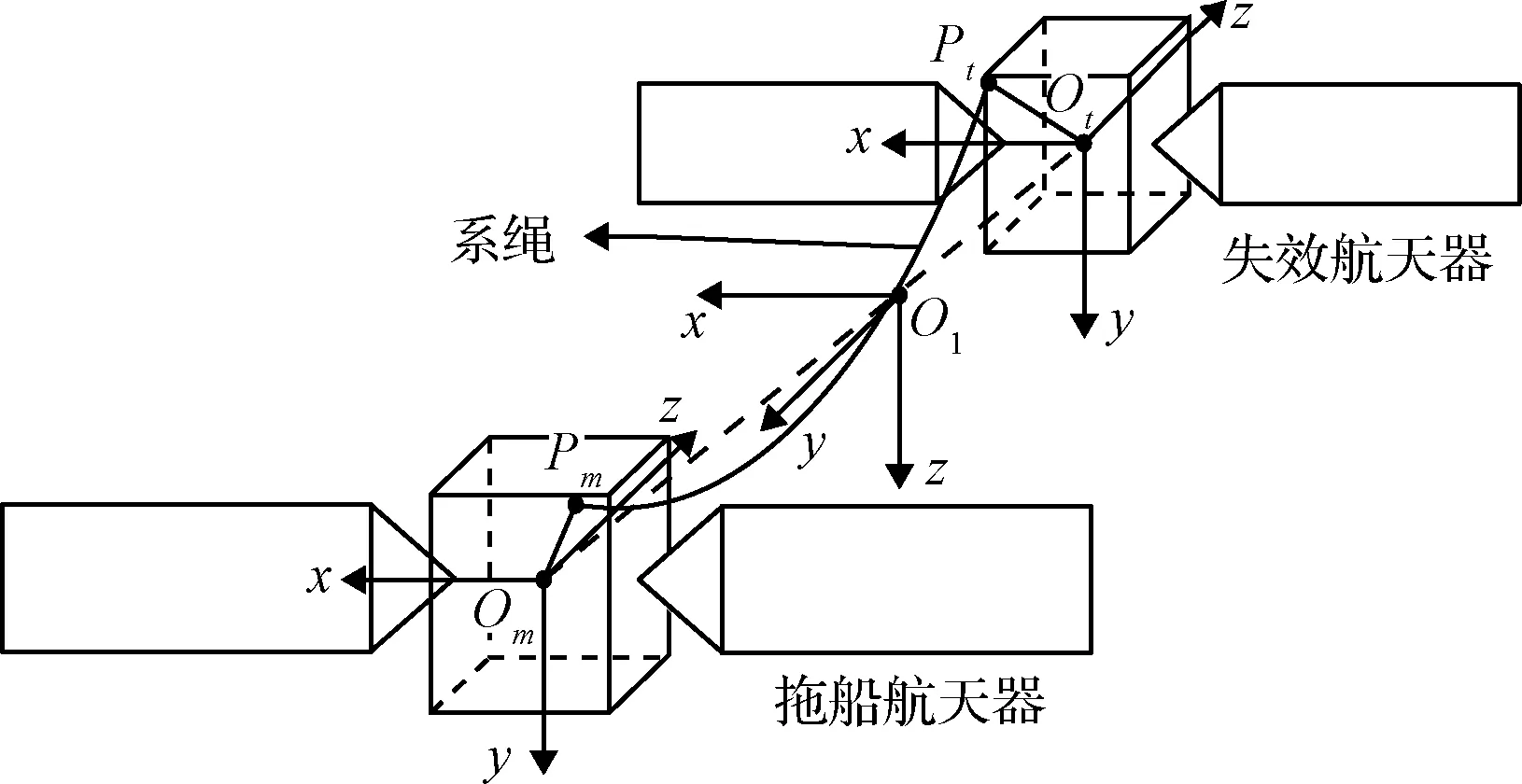
圖1 繩系拖曳系統組成與連接關系Fig.1 Composition and connection of TST system

1.2 系繩模型

建模過程中將系繩等效成不可壓縮的彈性桿模型，不計系繩質量，計入系繩彈性，根據實際情況考慮系繩阻尼特性。系繩張力只與形變量ΔL相關。定義拖船航天器與失效航天器上兩系繩牽掛點連線矢量Ltm，方向由失效航天器牽掛點指向拖船航天器牽掛點，則有：

(1)

式中:Cmbi,Ctbi分別為慣性系到拖船航天器和失效航天器本體坐標系的姿態轉移矩陣，pm,pt分別為本體系下兩星體系繩牽掛點矢量，rm,rt分別為拖船航天器、失效航天器質心在慣性系中的矢量。則系繩張力：

(2)

式中:L為系繩松弛時的原長，系繩形變量為：

(3)

D為系繩直徑，E為系繩彈性系數，η為系繩黏性阻尼系數，系繩張緊方向為系繩張力方向。

1.3 軌道動力學模型

繩系拖曳系統動力學建模中，系統所受外力中除拖船航天器軌控推力和地球中心引力外，忽略其它外部攝動。由此，地心慣性系下拖船航天器和失效航天器軌道動力學方程分別為：

(4)

(5)

式中:μ為地球引力常數，m1和m2分別為拖船航天器、失效航天器的質量，Fth為拖船航天器的軌控推力。

1.4 姿態動力學模型

忽略拖船航天器與失效航天器的柔性，將其均視為剛體，則可采用動量矩定律[12]建立拖船航天器與失效航天器姿態動力學方程：

(6)

(7)

式中:Im和It分別為拖船航天器、失效航天器的轉動慣量矩陣，ωm和ωt分別為兩航天器體角速度在各自本體坐標系下的投影，Cmbi和Ctbi為地心慣性系到拖船航天器、失效航天器本體系的姿態轉移矩陣，Tc為拖船航天器的姿態控制力矩[13]。

2 穩定性分析

2.1 模型簡化

為了對恒定張力條件下的繩系拖曳系統進行穩定性分析，采用圖2所示的簡化繩系拖曳系統模型。將拖船航天器視為質量為m1的質點，將失效航天器視為質量為m2、轉動慣量為Jx，Jy和Jz的剛體。系繩分別連接在碎片剛體質心和拖船航天器質點上，其質量可以忽略。

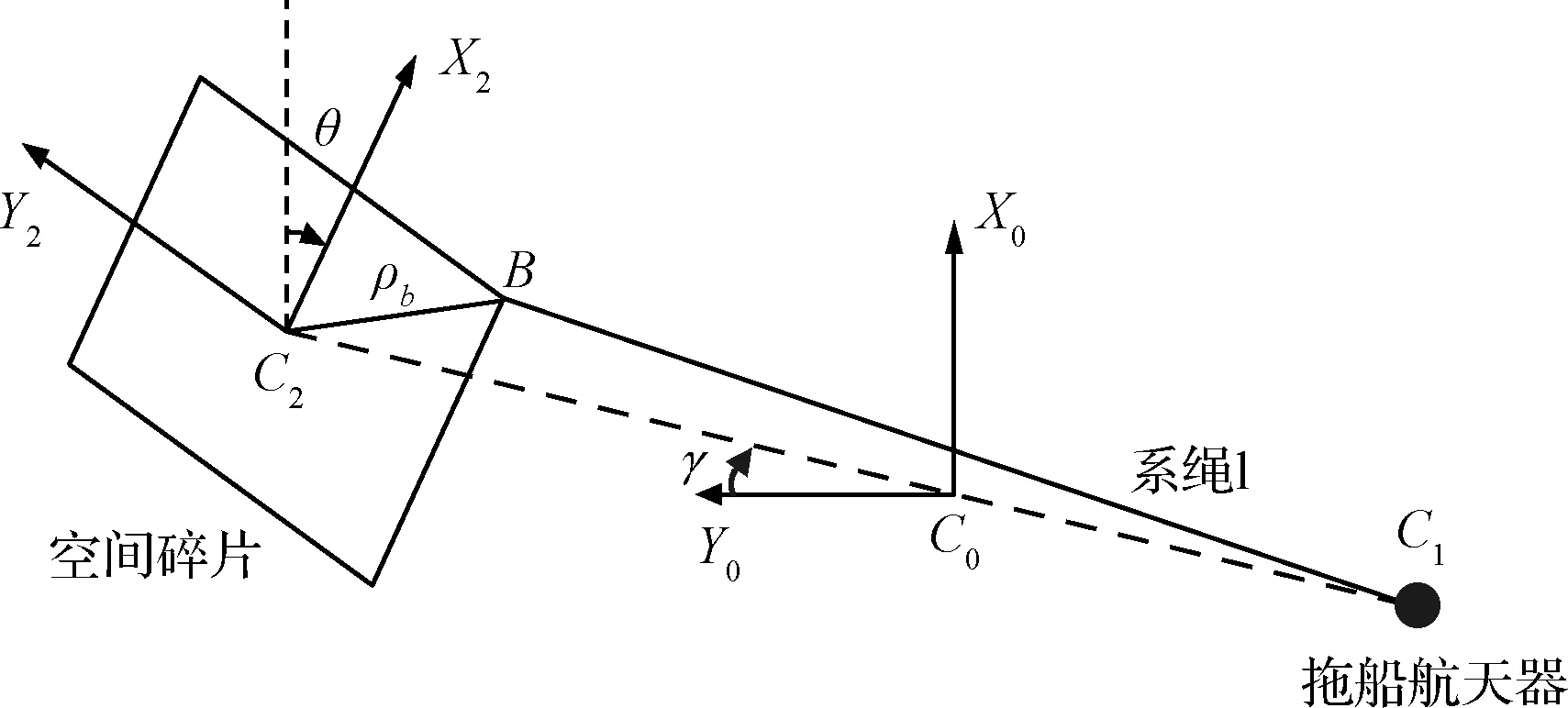
圖2 簡化的空間碎片繩系拖曳系統示意圖Fig.2 Simplified schematic diagram of TST system

定義當地鉛錘水平坐標系C0X0Y0Z0：原點取為系統質心C0，X0軸從地心鉛錘指向上，Y0軸在軌道平面內垂直于X0軸并指向系統的前進方向，Z0軸由右手法則定義。為描述碎片的姿態，定義原點在碎片質心、坐標軸為碎片剛體慣性主軸的體固坐標系C2X2Y2Z2。定義系統的廣義坐標如下：從當地鉛錘方向到X2軸的夾角為θ(順時針為正)；從當地水平方向到碎片和拖船質心連線的夾角為γ(順時針為正)；碎片和拖船的質心距為l。系繩張力Ft為常值，系統的運動在軌道平面內，質心的運動軌跡為圓軌道，利用拉格朗日方程可以得到空間碎片繩系拖曳系統的運動微分方程[13]如下：

(8)

(9)

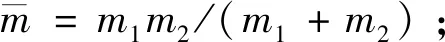
(10)

(11)

2.2 李雅普諾夫第一方法

李雅普諾夫第一法又稱間接法。它的基本思路是通過系統狀態方程的解來判別系統的穩定性。對于線性定常系統，只需解出特征方程的根即可作出穩定性判斷。對于非線性不很嚴重的系統，則可通過線性化處理，取其一次近似得到線性化方程，然后再根據其特征根來判斷系統的穩定性。

首先進行線性化，系統的平衡位置表示為θe和γe，將其代入系統方程式(10)和式(11)中則有：

(12)

γe=0

(13)

由式(12)可得系統兩個平衡解。由文獻[14]可知，θe在[0， π]范圍的平衡解為可行解，在[-π， 0]范圍的解不可行。本小節旨在分析可行解的穩定性，因此將僅考慮θe∈[0， π]的取值范圍。在平衡位置附近對系統方程線性化結果如下：

(14)

(15)

將系統方程改寫成狀態空間形式如下：

(16)

則系統的特征方程|λI-A|=0可寫為：

(17)

解得系統特征根為：λ1,2=0

(18)

(19)

在圖2中所示的坐標系定義下，xb>0，sinθe>0，因此sinθe/xb>0。事實上，當xb<0時，系統的可行平衡解將在[-π, 0]范圍內，仍然滿足sinθe/xb>0的條件。故λ3,4為純虛數，這說明系統是臨界穩定狀態。

李雅普諾夫第一法證明了系統在平衡解附近是臨界穩定的狀態。

2.3 李雅普諾夫第二方法

李雅普諾夫第二法又稱直接法。它的基本思路不是通過求解系統的運動方程，而是借助于一個李雅普諾夫函數來直接對系統平衡狀態的穩定性作出判斷。

將系統動力學方程式(10)和式(11)相加，得到如下形式：

(20)

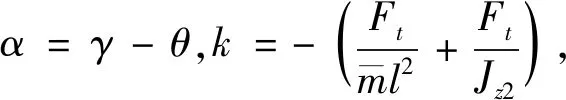
(21)

取李雅普諾夫函數為：

(22)

式中:yb<0，xb>0，對于任意α，均有V≥0，對李雅普諾夫函數式(22)求導則有：

(23)

這說明此時碎片的姿態角運動軌跡將落在某個特定曲面上:

日常實用性是奧迪R8 RWS的一大優勢，即使這乍一看像是某種劣勢—當車速在160公里/小時之內的情況下，R8 RWS為駕駛者帶來的聽覺和感受可能與普通的奧迪A4并無二致。然而，對于駕駛者而言，在體驗狂躁駕駛樂趣之余，感受生命中的沉靜與愉悅，也算是一件一舉兩得的樂事。

(24)

意味著運動軌跡將不會收斂于原點。

李雅普諾夫第二方法將上一小節所得的系統穩定性結論拓展到了大角度擺動情況，使結論不再局限于平衡解附近的鄰域。

3 控制律設計

3.1 姿態章動抑制控制律設計

考慮到目標為失效航天器且被飛網包裹時自旋情況不確定，認為其可能有一定角度的章動。為保證拖曳過程中不會發生系繩纏繞等風險，在對目標進行拖曳離軌前，應當對目標的章動角進行抑制，減弱拖曳過程中目標的章動對系統的影響。其姿態章動幅度大小可通過兩星連線與自旋軸間夾角體現，故可通過抑制兩星連線與目標自旋軸的夾角對目標姿態進行章動抑制。在拖曳過程中，當拖船航天器質心、網端繩結、目標質心三者共線情況下，系繩張力對目標姿態不會產生影響，此時兩星連線與目標本體自旋軸的夾角ξb為控制平衡位置，如圖3所示。

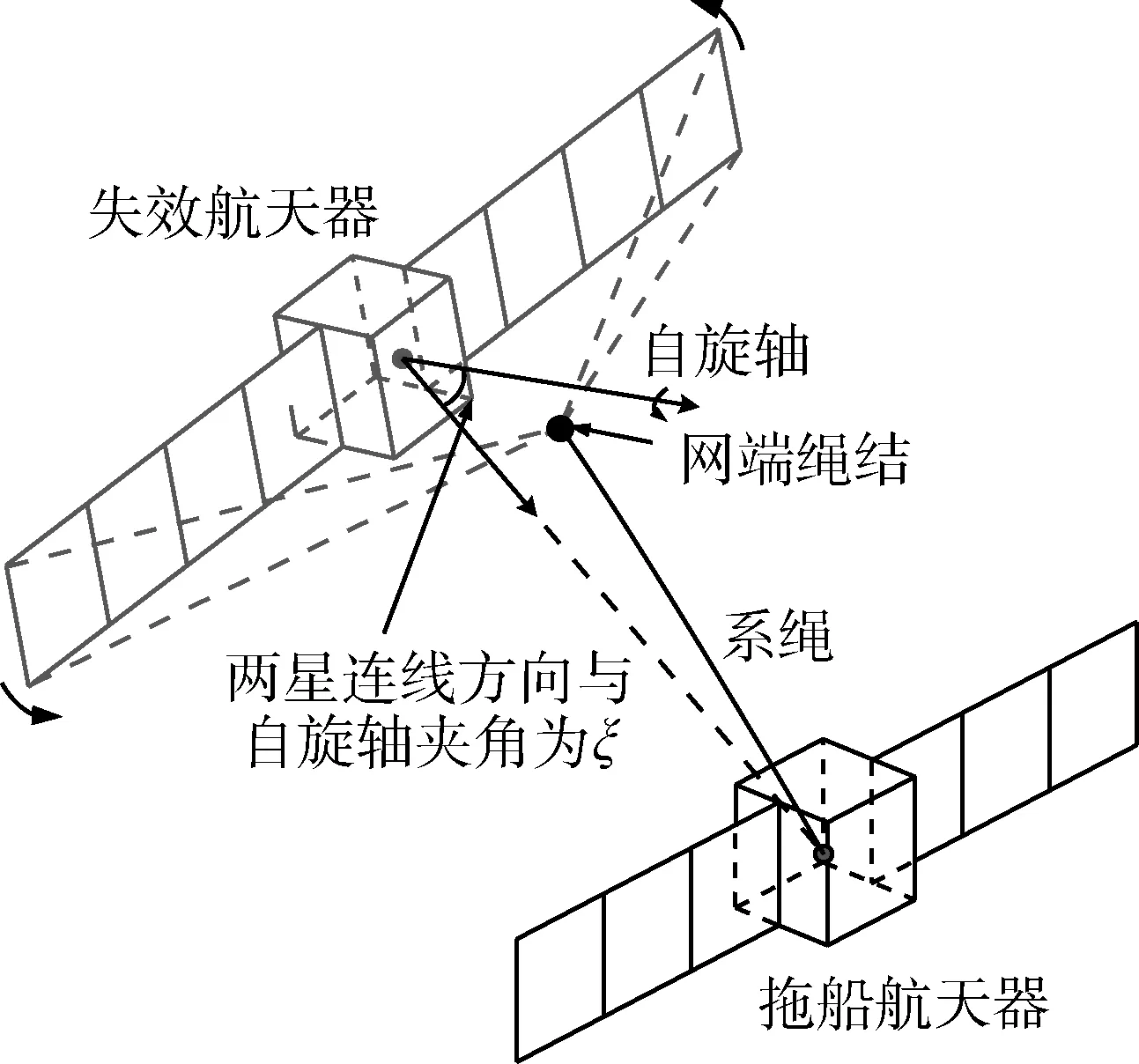
圖3 章動抑制示意圖Fig.3 Schematic diagram of debris nutation suppression

由于失效航天器姿態存在章動，故在拖曳過程中兩星連線與目標自旋軸的夾角以ξb為中心擺動。章動抑制的目的就是將兩星連線與目標自旋軸的夾角ξ控制在一定范圍內,由此設計章動抑制常值切換張力控制律為：

Ft=

(25)

式中:的章動角標稱值ξmax和ξmin根據控制要求的精度選擇，切換張力示意圖如圖4所示。

圖4 張力切換示意圖Fig.4 Schematic diagram of tension switch

3.2 組合體面內面外擺動控制律設計

在拖曳過程中需要對系繩的擺動進行有效鎮定，從而保證系繩和張力方向保持不變，同時還要把失效航天器自旋軸方向和系繩方向調整到期望的拖曳方向。

為了描述繩系組合體的姿態，引入面內角、面外角的概念。首先建立軌道坐標系S0，如圖5所示：Z軸沿地心連線方向由繩系組合體質心指向地球，X軸位于軌道平面內與Z軸垂直并指向軌道跡向,Y軸遵循右手準則，定義系繩方向在軌道面內的投影與軌道系X軸正向的夾角為面內角ε，系繩方向與軌道平面的夾角為面外角β。面內角表示了繩系組合體在軌道面內的相對位置，應控制面內角盡量小，避免大幅震蕩導致逆向拖曳；面外角表示拖曳時系繩的張力有無軌道法向的分力，應控制面外角盡量小，避免燃料的浪費。

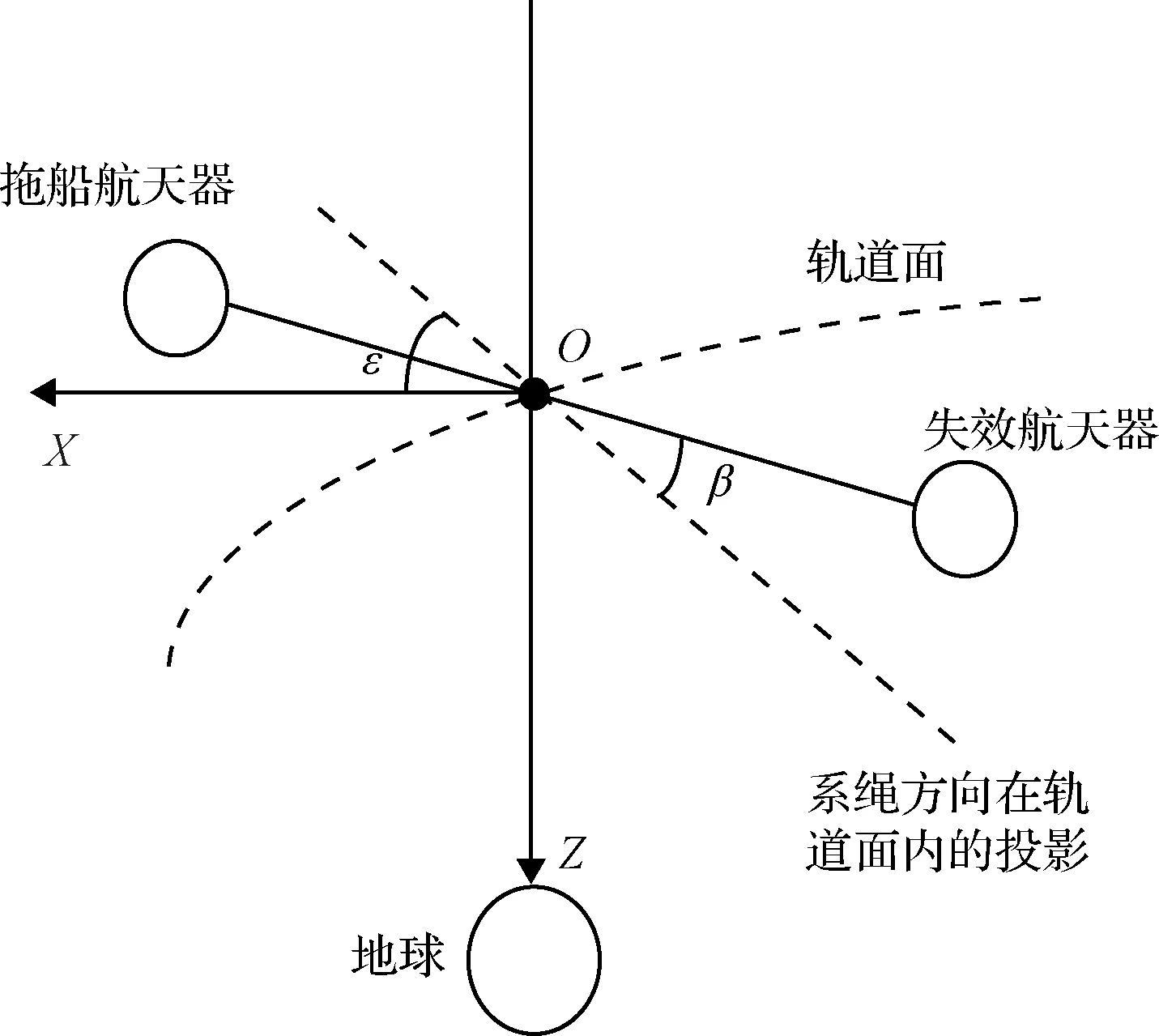
圖5 組合體面內外擺動示意圖Fig.5 Schematic diagram of in-plane and out-plane swing

面內外擺角ε=0°，β=0°時，繩系組合體姿態沿軌道跡向，拖曳變軌效率最高，故面內外擺角控制目標為ε=0°，β=0°。以拖船航天器噴氣推力為控制器輸入，采用基于相平面方法的組合體面內外擺角控制律，得到繩系組合體面內外擺動的穩定極限環，下文以面內擺角為例設計噴氣開關策略：

圖5中開關線A,D的方程如下：

(26)

(27)

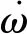
開關線控制參數設計：已知平臺推力器最小脈沖寬度Tmin；控制周期內最大脈沖寬度Tmax；組合體面內擺角控制力矩Tcε=Fzdm2/(m1+m2)；面內擺角轉動慣量Jε=m1m2d2/(m1+m2),d為兩星相對距離，Fz為拖船航天器軌控推力。

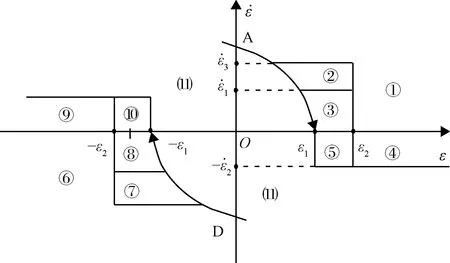
圖6 面內擺角控制開關線Fig.6 In-plane swing angle control switch line

4 仿真校驗

拖曳控制全過程方案為：選取兩種切換張力為Ftb= 4 N和Fts=2 N，全程采用常值切換控制律抑制失效航天器的姿態章動，并同時采用基于相平面控制原理的控制律抑制組合體面內面外擺動，保證拖曳過程的安全平穩，達成將碎片目標近地點高度抬高350 km的控制目標，仿真結果如下：

表1 面內擺角控制相平面區域范圍及每個區域機開機時間Table 1 Phase plane area range and startup time of each area machine controlled by in-plane swing angle

仿真結果表明，在該種全過程拖曳控制方案下，碎片目標的姿態章動始終能夠得到很好地抑制；繩系組合體面內面外擺角能得到很好地鎮定；完成拖曳控制全過程的所用時間為9.02 h，碎片目標近地點高度被抬高350 km，實現了將空間碎片從地球同步軌道轉移至墳墓軌道的目標，達到了預期的控制效果。與文獻[9]和文獻[15]中采用的時變張力控制方法的仿真結果對比，采用常值張力控制方法雖然響應速度稍慢，但也完全能夠滿足工程任務的時間要求，且對目標姿態章動和組合體面內外擺動的控制精度更高。

5 結 論

本文針對常值拉力作用下的空間碎片繩系組合體的拖曳離軌問題，首先利用牛頓歐拉法建立了組合體動力學模型，并通過拉格朗日方程得到簡化的動力學模型；然后利用李雅普諾夫第一法證明了系統在平衡解附近具有臨界穩定性，并通過李雅普諾夫第二法將系統穩定性推廣到大角度擺動情況，使結論不再局限于平衡解附近的鄰域；得出穩定性結論后，設計常值拉力切換控制律抑制空間碎片的姿態章動，研究基于相平面原理的控制律抑制繩系組合體的面內面外擺動。通過對空間碎片軌道轉移全過程的仿真分析表明，采用常值拉力切換能夠實現拖曳過程的精確控制，設計的控制律能夠達到預期的控制效果，為今后將恒張力拖曳控制方法應用于空間碎片主動清除任務打下理論基礎。

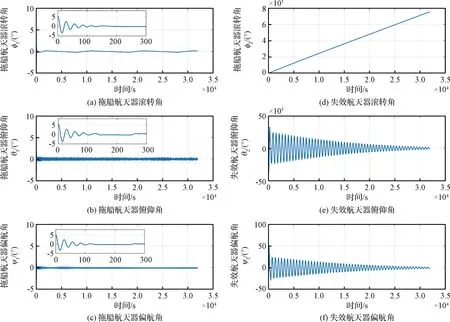
圖7 拖船航天器和失效航天器姿態角變化曲線Fig.7 Curve of change of tug spacecraft and invalid spacecraft attitude angle

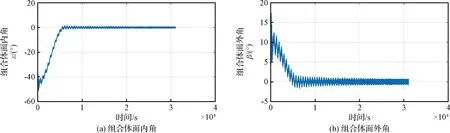
圖8 繩系組合體面內擺角和面外擺角變化曲線Fig.8 Curve of change of in-plane and out-plane swing angle

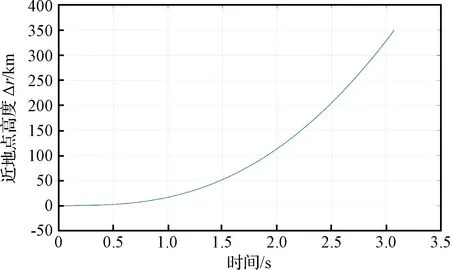
圖9 近地點高度變化量曲線Fig.9 Change of the altitude of the perigee height