臨近空間高空氣球囊體材料的蠕變試驗和數值分析

張遠平，姜魯華，宋 林，呂 靜，楊燕初

(1. 中國科學院光電研究院， 北京 100094； 2. 中國科學院大學， 北京 100049；3. 中國科學院高能物理研究所， 北京 100049)

臨近空間主要是指大氣層中的平流層，在對地觀測、局部安防、移動通信等軍民應用需求的強力推動下，臨近空間持久區域駐留飛行器的發展受到世界各國高度關注[1-2]。在此高度可長時間飛行的飛行器有臨近空間浮空器、太陽能無人機等。臨近空間浮空器主要有平流層飛艇、高空科學氣球等。高空科學氣球是指工作在平流層高度區域的輕于空氣的浮空飛行器，也稱高空氣球或者平流層氣球[3]。由于高空科學氣球飛行在平流層，飛行高度較高、對地觀測范圍較大、效費比高，因此在科學研究和軍事方面都有很大的使用前景，目前美國、日本以及歐洲一些國家均在使用高空科學氣球進行各項試驗和研究。

臨近空間浮空器囊體材料作為浮空器的主要材料，其性能直接影響浮空器的應用效能[4]，比如囊體可承受壓力、有效載荷、使用壽命等。臨近空間飛艇囊體材料一般由多層薄膜與高強纖維織物復合而成[5]，而高空氣球囊體材料主要是聚乙烯薄膜為主的高分子薄膜材料。臨近空間飛艇是目前的研究熱點，對于其囊體復合材料的各類性能已經有了深入研究。高空氣球目前應用不是很廣泛，其研究相對于臨近空間飛艇要少一些。NASA研究人員對高空氣球進行了多次室內模型測試、材料測試及試飛試驗，對于囊體材料的深入研究一度成為NASA高空氣球的主要研究內容之一[6]。NASA還對3種不同設計的高空氣球進行了囊體材料性能測試和耐壓試驗[7]。Henderson針對高空氣球囊體材料Stratofilm372和AstrofilmE2分別建立了室溫以及低溫狀態下的單軸蠕變屈服結構模型，用該計算模型可以直接從應力狀態得到應變和變形[8]。美國德州的A&M大學提出了一種新的分析方法，動態機械分析法，利用動力學方法對常用薄膜類材料的黏彈性蠕變性能進行了試驗分析，并建立了非線性結構模型[9]。楊希祥等對平流層長航時氣球上升過程進行了分析研究，得出了囊體材料的物理參數帶來的影響[2]。麻震宇等對臨近空間浮空器囊體進行了超壓特性和承載特性分析[10]。隨著飛行任務復雜化，從零壓型的高空氣球逐步向長航時的超壓型的高空氣球發展，在長時間受壓情況下，囊體材料會發生緩慢的蠕變。因此本文設計了蠕變試驗，對臨近空間高空氣球囊體材料的蠕變特性進行了測試，結合試驗結果對囊體材料進行了分析仿真，并給出了相關的蠕變模型參數。

1 蠕變試驗

針對某型號高空氣球囊體材料DPE-3進行研究，該材料由高分子材料組成，厚度為38 μm，呈透明狀，斷裂伸長率為512%。蠕變試驗分為一、二、三組，拉伸強度分別為0.625 N/cm、1.25 N/cm、2.5 N/cm，每組試驗6個試樣。該材料經緯向強度基本一致，因此不區分經緯向，作為各向同性材料進行試驗分析。

試驗采用自行設計的蠕變試驗架，如圖1所示，在室溫下進行蠕變試驗。囊體材料試件被制作為啞鈴型，有效試驗長度為180 mm，寬度為20 mm，如圖2所示。

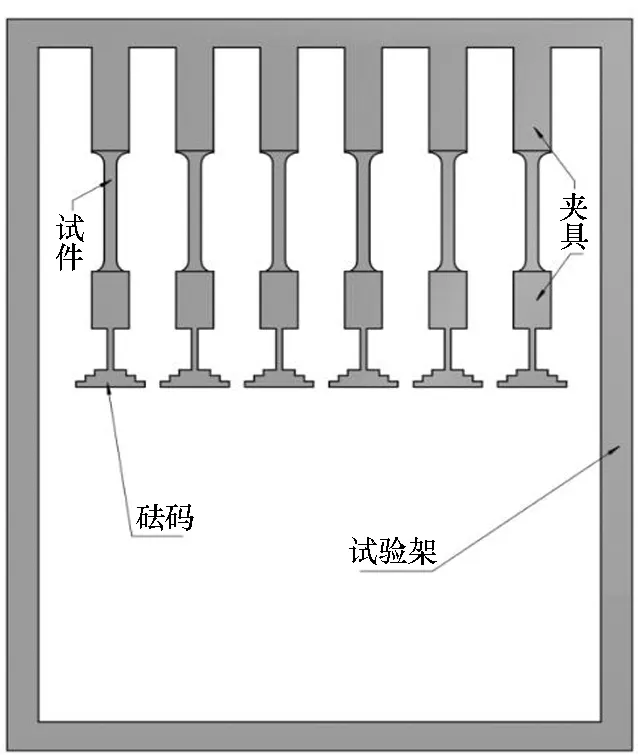
圖1 蠕變試驗架Fig.1 Creep test frame

圖2 DPE-3囊體材料蠕變試驗試件Fig.2 Creep test specimens of envelope material for DPE-3

將試件兩端利用蠕變試驗架中的特制夾具夾緊，下端夾具為輕型硬塑料，重量為0.5 N。以夾具重量0.5 N作為預張力確保樣條處于垂直狀態，并保持10 min，且將形變清零后加載至所需載荷，然后將時間清零，開始進行蠕變性能測試。在載荷的作用下，試件產生形變，記錄下來的形變量(拉伸位移)即為蠕變量。

臨近空間高空氣球在超壓設計狀態時，會承受一定的內壓。在開展本次蠕變試驗之前，本項目組已進行多次超壓型高空氣球的實際飛行試驗，根據實際承受的內壓計算囊體材料的受力情況，其囊體材料承受的最小拉力在0.625 N/cm左右，工作拉力在1.25 N/cm左右，最大拉力在2.5 N/cm左右。

試驗分別進行一、二、三組，根據球體實際受力情況，設置拉伸強度分別為0.625 N/cm、1.25 N/cm、2.5 N/cm。由于試件寬度為2 cm，則一、二、三組試驗中每個試件的載荷分別為1.25 N、2.5 N、5 N。每組蠕變試驗做6個試樣。其中試驗組一的第2和第4個試樣以及試驗組三的第5個試樣在試驗結束時發生明顯的切向變形，原因是裝夾不對稱造成統一橫截面所受應力不均勻，該三個試樣的試驗結果無效。

圖3～5分別給出了常溫狀態下，三組蠕變試驗的時間-拉伸位移實驗結果和最小二乘法的擬合曲線。

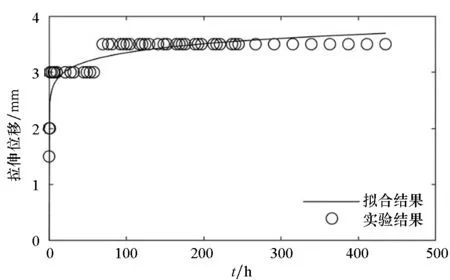
(a) 試樣1(a) Sample 1

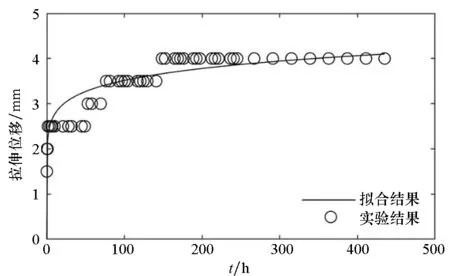
(b) 試樣2(b) Sample 2

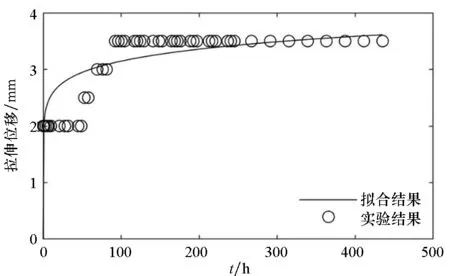
(c) 試樣3(c) Sample 3

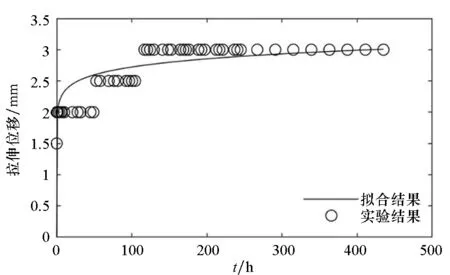
(d) 試樣4(d) Sample 4

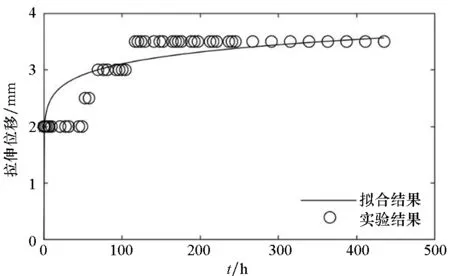
(e) 試樣5(e) Sample 5

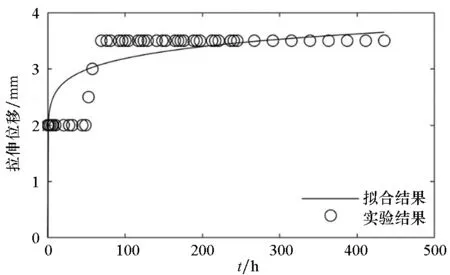
(f) 試樣6(f) Sample 6圖3 拉伸強度為0.625 N/cm的時間-拉伸位移曲線Fig.3 Time-tensile displacement curves of 0.625 N/cm

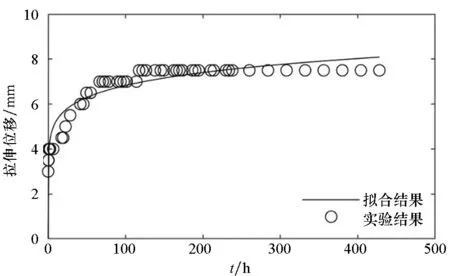
(a) 試樣1(a) Sample 1

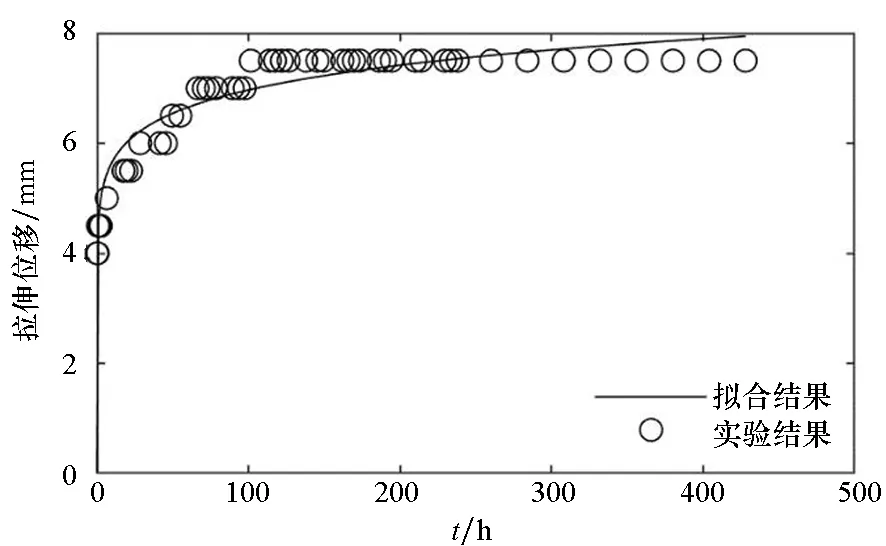
(b) 試樣2(b) Sample 2

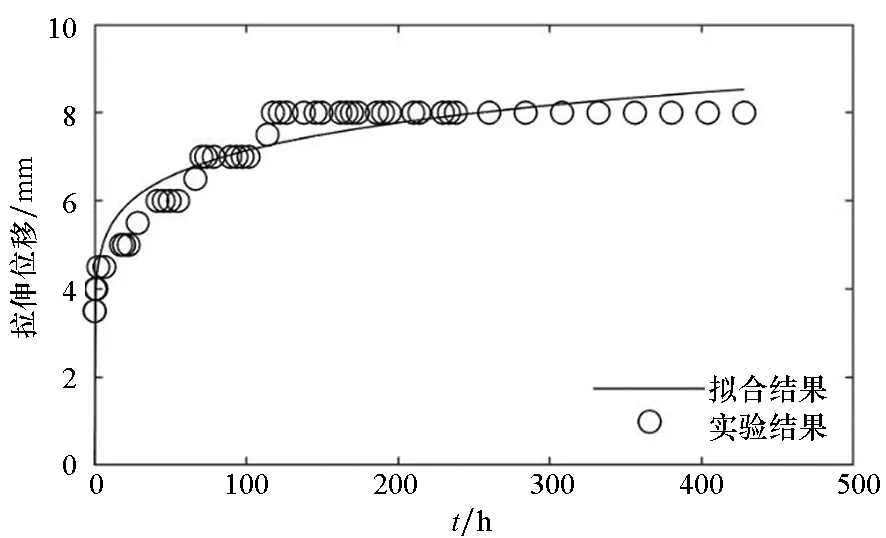
(c) 試樣3(c) Sample 3

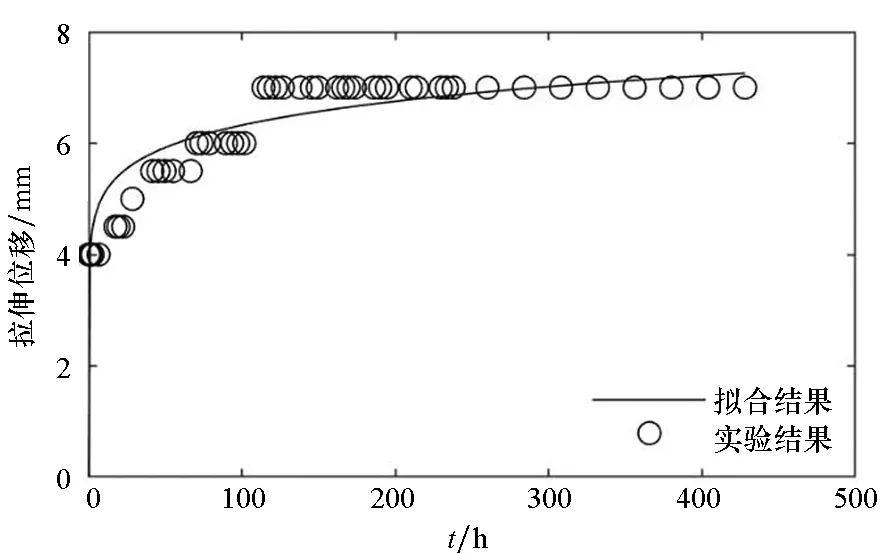
(d) 試樣4(d) Sample 4

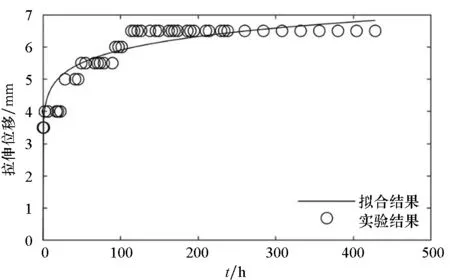
(e) 試樣5(e) Sample 5

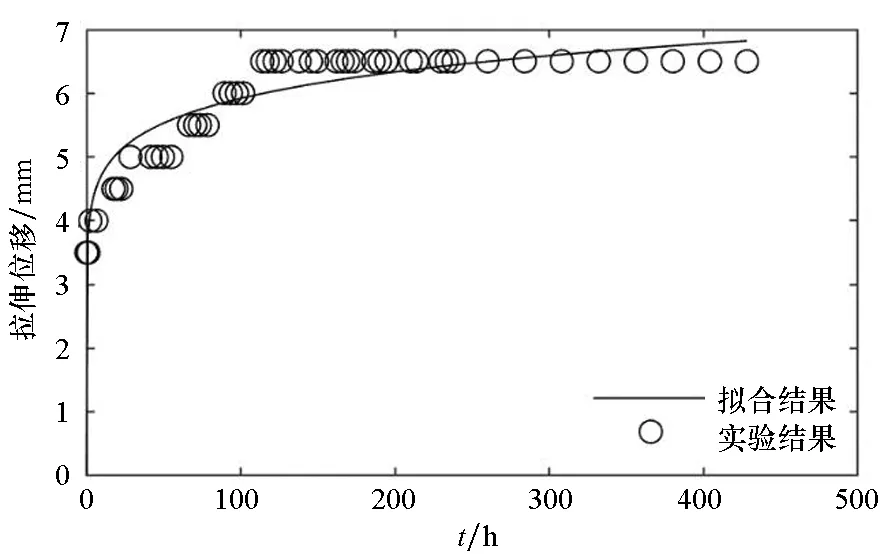
(f) 試樣6(f) Sample 6圖4 拉伸強度為1.25 N/cm的時間-拉伸位移曲線Fig.4 Time-tensile displacement curves of 1.25 N/cm

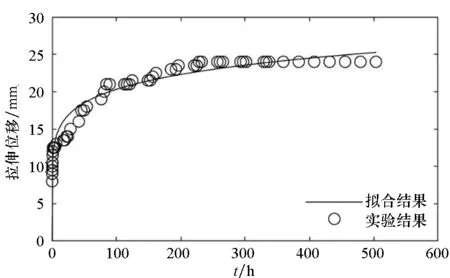
(a) 試樣1(a) Sample 1

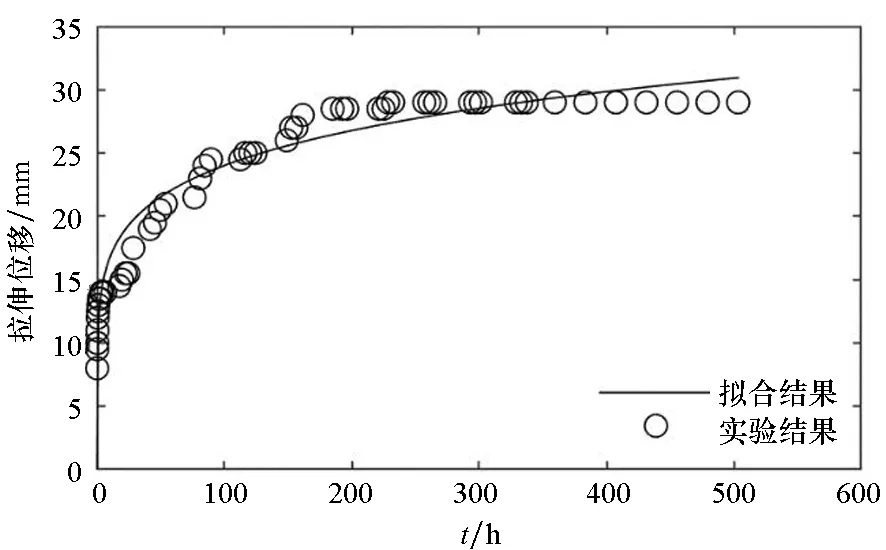
(b) 試樣2(b) Sample 2

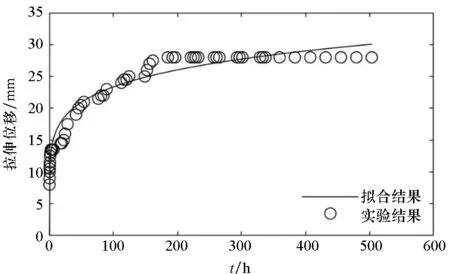
(c) 試樣3(c) Sample 3

(d) 試樣4(d) Sample 4

(e) 試樣5(e) Sample 5

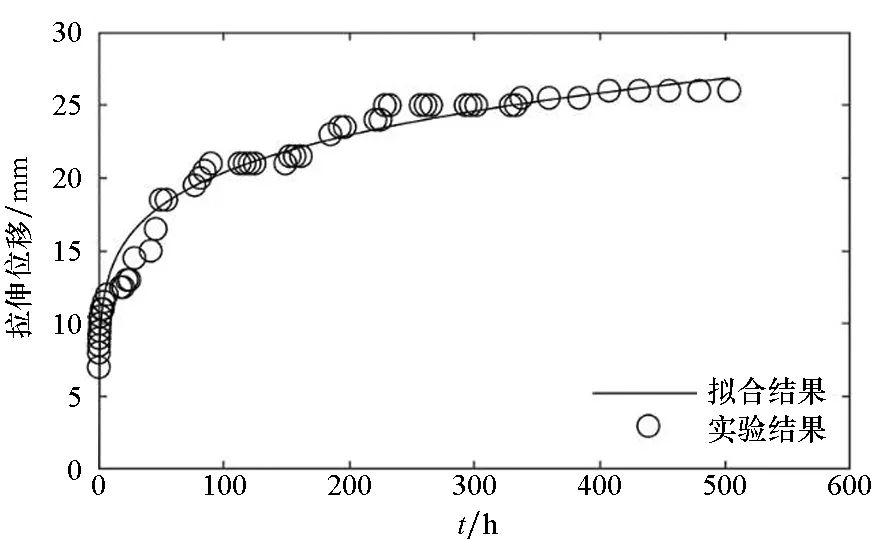
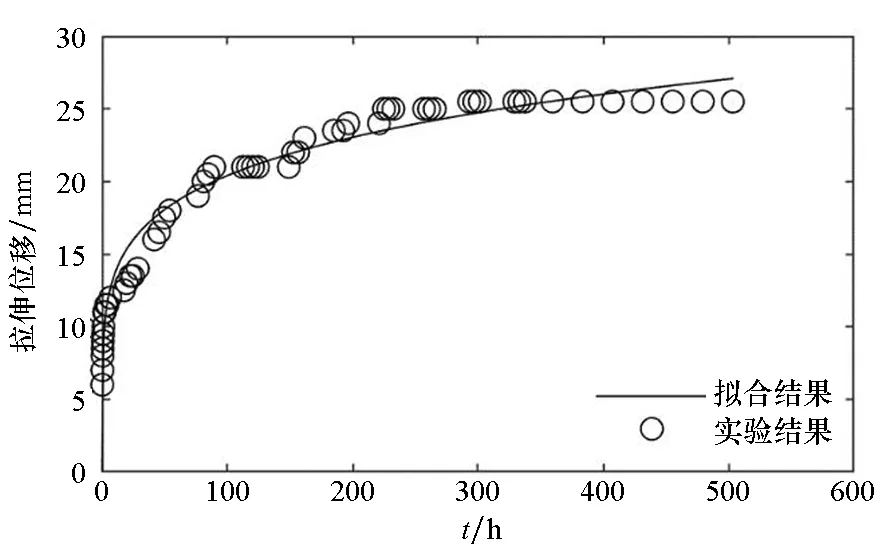
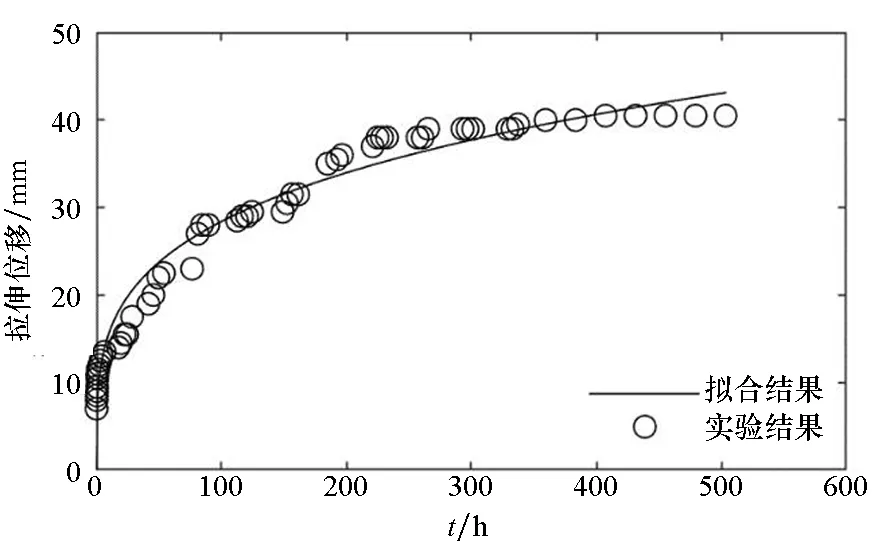
(f) 試樣6(f) Sample 6圖5 拉伸強度為2.5 N/cm的時間-拉伸位移曲線Fig.5 Time-tensile displacement curves of 2.5 N/cm

對圖3～5的蠕變結果進行比較可以發現：隨著載荷的增大，蠕變速率增大，蠕變量增大。高空氣球囊體材料DPE-3由高分子材料組成，從高分子材料的結構來分析，在載荷增大的情況下，應力使得高分子材料內部松弛、折疊片松弛、界面滑移等情況更為明顯，從而表現出蠕變量的增大。

因此，高空氣球囊體材料DPE-3的蠕變性能跟載荷的大小有較為明顯的關系：在小載荷情況下具有較好的抗蠕變性能；在載荷增大的情況下抗蠕變性能下降，蠕變速率增大，蠕變量增大。

2 陳化理論參數確定

根據陳化理論，在溫度一定的情況下，材料蠕變的應變、時間和應力之間存在一定的關系ε=f(σ,t)。對于多數材料應力和應變之間存在較強的非線性關系，在變應力情況下，可以將蠕變的應變、時間和應力的關系表達為：

ε=Aσntm

(1)

式中，A、m、n均為材料參數，由蠕變試驗的數據擬合進行確定。

將式(1)左右兩邊對t求導，可以得到：

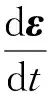
(2)

式中，A1=A·m,M=m-1。

根據陳化理論，將三組實驗結果進行最小二乘法擬合，獲得陳化理論參數A=0.002 541，n=1.676，m=0.153 2，A1=0.000 389 281 2,M=-0.846 8。利用這些參數，可以根據陳化理論計算囊體材料DPE-3的蠕變應變。

圖6為利用陳化理論計算擬合的囊體材料DPE-3蠕變應變關于時間和應力的三維曲面圖。根據陳化理論進行計算，可以得到囊體材料DPE-3在不同應力、不同蠕變時間下的蠕變應變，從而判斷材料在該使用條件下的蠕變性能。

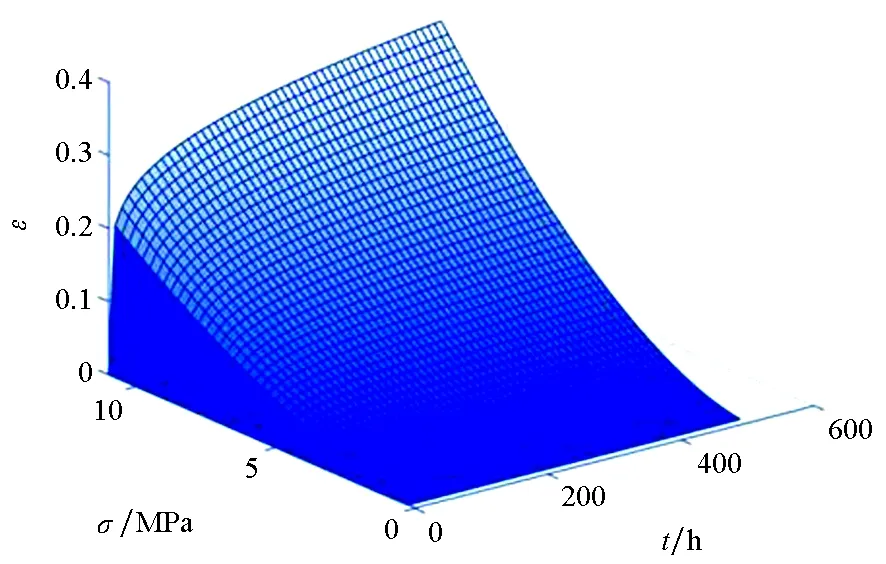
圖6 蠕變應變關于時間和應力的陳化理論擬合三維圖Fig.6 Three-dimensional fitting of creep strain with aging theory of time and stress

3 有限元數值分析

根據試驗建立相應的有限元模型，對其用有限元分析方法進行蠕變計算分析，具體材料參數和幾何參數見表1，將囊體材料DPE-3作為各向同性材料進行分析，與實際材料的屬性相符。

蠕變模型選擇陳化理論模型Norton，模型參數根據陳化理論確定，n=1.676,A1=0.000 389 281 2,M=-0.846 8。

陳化理論模型Norton是用全量形式進行描述，并且在方程中有時間參數t。陳化理論的表達形式適合于恒定的載荷或者變化非常緩慢的載荷。在浮空器的飛行過程中，由于囊體需要保持一定的壓力，作用在囊體材料上的載荷變化比較緩慢，從蠕變狀態來說符合陳化理論的主要特點。

分別進行三組有限元數值分析，試樣一側固定約束，一側承受不同的拉伸力，載荷條件見表2。

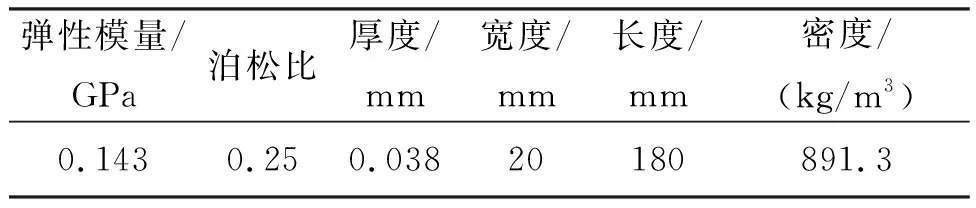
表1 有限元模型的材料參數和幾何參數

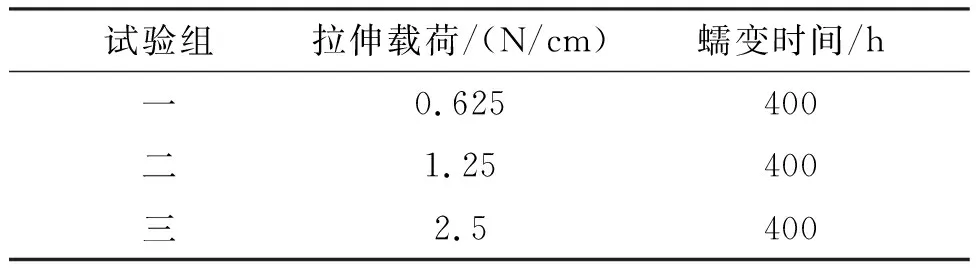
表2 三組有限元模型的載荷條件

圖7為不同載荷作用下，三組有限元分析試樣經過400 h蠕變計算所得的拉伸位移。表3給出了對應三種工況下，試驗、陳化理論模型計算和有限元分析獲得的蠕變量。

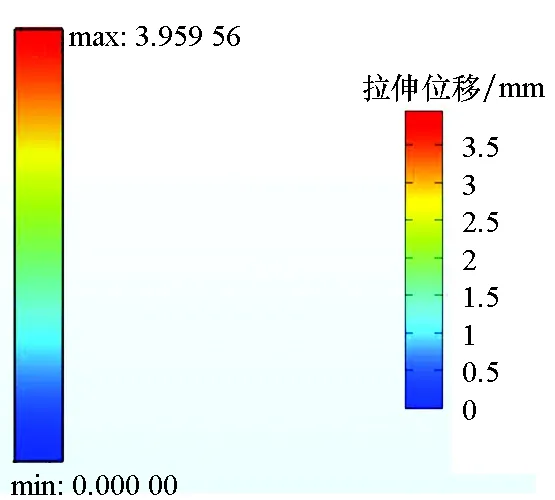
(a) 0.625 N/cm

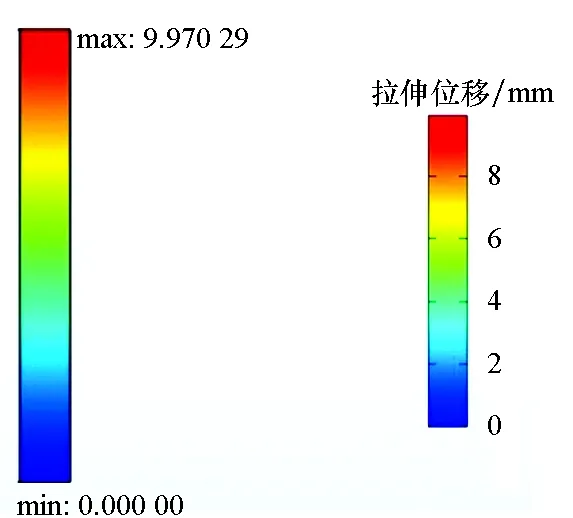
(b) 1.25 N/cm

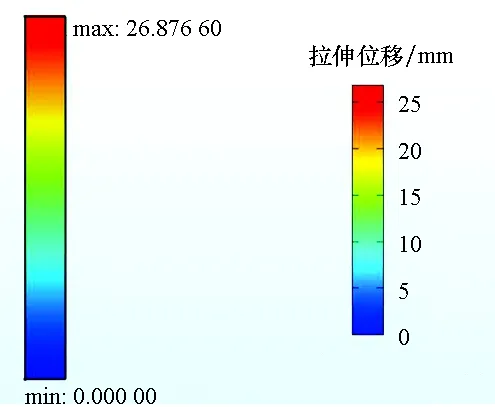
(c) 2.5 N/cm圖7 不同拉伸應力條件下400 h后試樣的蠕變量Fig.7 Creep of specimens after 400 h under different tensile stress conditions

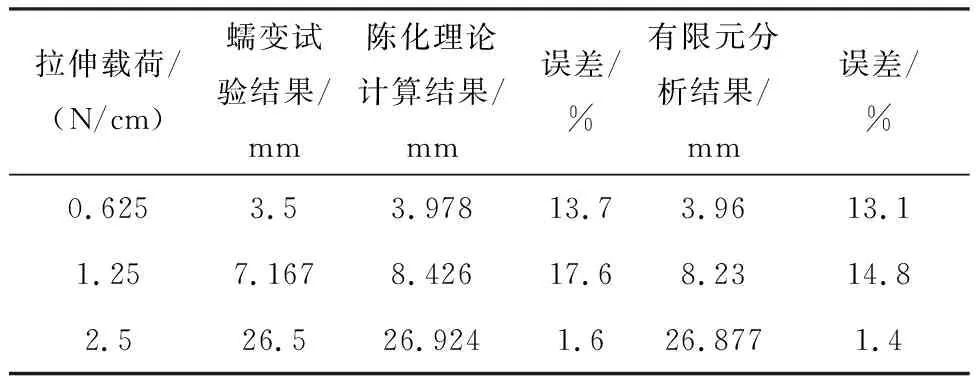
表3 不同拉伸應力條件下400 h蠕變后材料試驗、陳化理論和有限元分析的拉伸位移Tab.3 Tensile displacements of material test, aging theory and finite element analysis after 400 h creep under different tensile stress conditions

通過比較試驗結果、陳化理論計算結果以及有限元分析結果可以發現：隨著載荷的增大，蠕變量增大，蠕變速率增大。當載荷為該囊體材料實際承受的最大拉力時，陳化理論計算結果和有限元分析的結果都非常接近蠕變試驗結果。

在小載荷的情況下，由于高分子材料在常溫下處于玻璃態，鏈段都處于被凍結狀態，并且受鍵長、側基和鍵角等內部因素的影響較大，蠕變速率較小，蠕變量較小，同時蠕變量也容易不穩定。隨著載荷的增大，蠕變速率增大，蠕變量增大，載荷成為蠕變量的主要影響因素，材料內部因素的影響減小，此時實際的蠕變試驗結果更接近理論結果。

在載荷為0.625 N/cm、1.25 N/cm和2.5 N/cm三種實際受力工況下，陳化理論計算結果和有限元分析結果都比較接近實際蠕變試驗結果，因此用DPE-3作為高空氣球的囊體材料時，可以用本文的計算方法和有限元分析模型進行仿真和計算蠕變量，對材料的蠕變性能進行分析研究。

4 結論

通過蠕變試驗給出了臨近空間高空氣球囊體材料DPE-3在不同應力下(0.625 N/cm、1.25 N/cm、2.5 N/cm)的時間-拉伸位移曲線，從試驗結果分析可知，應力越小，蠕變速率越小，蠕變量越小，隨著載荷的增大，蠕變速率增大，蠕變量增大。

根據蠕變試驗數據，用最小二乘法進行曲線擬合，確定了囊體材料DPE-3的陳化理論參數。并以陳化理論建立了有限元分析模型，分析不同應力條件下(0.625 N/cm、1.25 N/cm、2.5 N/cm)蠕變時長為400 h的時間-拉伸位移結果。將陳化理論計算結果、有限元分析結果與蠕變試驗結果進行比較，驗證了陳化理論計算結果和有限元分析結果在一定程度上的準確性。本文的陳化理論計算方法和有限元分析模型，可用于分析和計算囊體材料DPE-3的蠕變性能，為臨近空間高空氣球的設計和分析提供參考。