高中圓錐曲線教學與數(shù)學思想方法的滲透

張忠偉

摘 要：數(shù)學對我國經(jīng)濟水平的提升及社會的進步有著至關重要的作用，而數(shù)學思想是學習數(shù)學的靈魂。圓錐曲線的學習是高中重點教學內容，在教學過程中，教師應結合數(shù)學思想在表象的知識學習過程中使學生掌握數(shù)學核心思想。

關鍵詞：圓錐曲線 教學方法 教學思想 滲透策略

圓錐曲線是高中重點教學內容，也是高中數(shù)學學習過程中的難點知識。圓錐曲線與其他知識相比，更加抽象，導致學生難以理解[1]。因此，在圓錐曲線學習的過程中，高中數(shù)學教師應充分利用數(shù)學思想進行教學，使學生通過數(shù)學思想了解圓錐曲線的抽象概念。

一、圓錐曲線的學習在高中數(shù)學中的地位

圓錐曲線知識內容屬于解析幾何中的重要組成部分，也是數(shù)學高考的重點及熱點知識。圓錐曲線知識的考點主要是向量、三角函數(shù)、平面幾何等其他相關知識緊密結合起來的，該類型的題目主要對學生問題解決能力及問題分析能力進行考察。

二、圓錐曲線的學習對數(shù)學思想培養(yǎng)的作用

1.培養(yǎng)學生計算能力

在高中數(shù)學考試時，學生受到考試時間的限制會產生緊張心理。因此，學生在考試過程中計算準確率較低。想要培養(yǎng)學生數(shù)學學習能力并提升其數(shù)學計算能力，最快的方式就是鍛煉圓錐曲線計算。在圓錐曲線學習過程中，涉及多種計算方法，而且圓錐曲線知識與其他學習模塊相比，對計算的精準度具有更高的要求。

2.培養(yǎng)學生數(shù)學思考能力

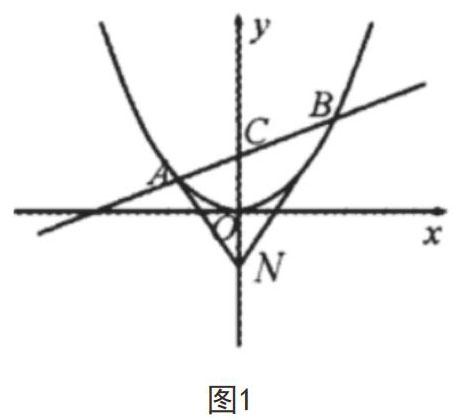
在圓錐曲線的學習過程中，教師要適當引導學生對同一問題進行多重角度的思考。由于圓錐曲線的知識較為抽象，學生想要對知識進行充分的理解及運用，就應在多角度對其進行思考及研究。這種教學方式既能夠培養(yǎng)學生數(shù)學邏輯思維，還能夠鍛煉多角度思考問題并解決問題的能力。例如，對平面直角坐標系xoy進行計算，直線與拋物線（x2=2py）過定點C相交在A、B點，詳情如圖1。求以下問題：（1）N為C坐標系原點O的對稱點，計算ANB面積;（2）垂直與y軸的l直線是否存在，l被AC直徑圓截得的恒定值，如存在，計算出方程，如不存在，闡述原因。根據(jù)對該題目的分析可知，CN=2P為定值，將△ANB的面積進行分割，分別為△ANC、△CNB，|CN|是底邊，A點到y(tǒng)軸的距離為x1，B點到y(tǒng)軸的距離為x2，想要求出x2+x2和x2x2，將直線與拋物線最終聯(lián)立最終求解就可以了。

3.培養(yǎng)學生歸納整理思維

對所學的數(shù)學知識進行歸納整理也是數(shù)學思想的核心內容。學生在對圓錐曲線知識進行學習的過程中，應將以往學習的知識點應用在其中[2]。這樣能夠對知識點進行有效的分類及梳理，并對各知識點之間進行關聯(lián)及區(qū)分，這種教學方式能夠培養(yǎng)學生的分類整理能力，使其在日后學習過程中對學習的知識點進行有效梳理與總結。

4.培養(yǎng)學生有效運算方法

教師應引導學生從多個角度對同一個問題進行思考解決，從而培養(yǎng)其運算準確率及運算速度。在圓錐曲線的學習過程中，教師應引導學生對相同的問題進行多方位思考，從而培養(yǎng)學生聯(lián)想能力、觀察能力及對比意識。學生通過自我觀察、比較、思考，找到最佳問題解決方法。在教師對問題講解后，應引導學生去對比不同解題方法之間的優(yōu)點與缺點，從而找到最佳解題思路。解題思路的反復鍛煉與選擇能夠培養(yǎng)學生數(shù)學解題意識，并使其準確的選擇解題途徑，與此同時，還能夠提升其運算準確率及運算速度。

三、數(shù)學思想在圓錐曲線學習過程中的滲透

首先，根據(jù)對數(shù)形結合思想在圓錐曲線學習過程中的滲透研究可知，數(shù)字缺少圖形時便少了直觀思路，圖形缺少數(shù)字時便無法將其細化。因此，應將數(shù)字與圖形相結合，才能夠將抽象的概念變得生動形象。尤其在圓錐曲線的學習過程中，有許多抽象的教學理念，教師應利用數(shù)形結合思想將難以理解的概念變得通俗易懂，從而幫助學生找到解題突破口。

其次，通過對類比思想在圓錐曲線學習過程中的應用研究可知，類比思想是學生對已有知識進行分類整理，從而達到舉一反三的教學目的[3]。類比思想在圓錐曲線學習過程中的應用能夠有效提升學生學習效率，并減輕其學習負擔，還能夠激發(fā)學生們的數(shù)學學習興趣。

最后，圓錐曲線作為高中數(shù)學學習的重點及難點知識，教師在對該知識進行教學過程中，應采用科學合理的辦法將數(shù)學思想滲透在知識講解中，使學生通過先進科學的數(shù)學思想及解題方法提升自身學習效率，從而達到高效教學。

結語

根據(jù)本文敘述可知，圓錐曲線是高中重點教學內容，也是高中數(shù)學知識的精華。而且圓錐曲線知識內容的學習對數(shù)學思想的培養(yǎng)有著重要的作用，學生能在知識學習過程中鍛煉計算能力，并使計算準確度得以有效提升。除此之外，還能夠學會對同一問題進行多角度思考，養(yǎng)成數(shù)學邏輯思維，并鍛煉解題能力。圓錐曲線知識的學習還能夠培養(yǎng)學生歸納整理思維，不光如此，還能夠幫助其學會高效運算方法，在日后數(shù)學學習過程中能夠以最快的速度找到最佳解題思路。還應將圓錐曲線相關的知識與學生以往學習的知識進行有效結合，這種教學方法不僅將原有知識進行靈活運用，還將各知識點之間進行相互關聯(lián)，只有這樣，才能夠使學生在掌握所學內容的基礎上，收獲圓錐曲線的知識內容[4]。

參考文獻

[1]吳冬梅.高中圓錐曲線教學與數(shù)學思想方法的滲透[J].數(shù)理化學習（教育理論），2017，（4）：33-34.

[2]吳冬梅.高中圓錐曲線教學與數(shù)學思想方法的滲透[J].數(shù)理化學習（教研版），2017，（004）：33-34.

[3]馬強.高中數(shù)學雙曲線教學思考與探索[J].中外交流，2019，（5）：272-273.

[4]任俊.探析高中數(shù)學教學中數(shù)形結合方法的運用[J].學周刊，2018，24（24）：81-82.