基于數據融合的航空發動機多余度智能傳感器故障診斷

翟旭升，楊仕美，段朋振，陶 燁

(空軍工程大學航空機務士官學校，河南信陽 464000)

1 引言

在航空發動機控制系統中，大量傳感器分布于高溫及強振動等惡劣環境中，難免發生故障。據統計，發動機控制系統故障中，傳感器及執行機構故障占控制系統總故障的80%以上[1]，因此對傳感器進行故障診斷的問題顯得非常突出。為提高傳感器的可靠性并具備故障診斷與隔離功能，傳感器本身正朝著多余度化、智能化方向發展，特別是在國內外學者目前正在研制的航空發動機分布式控制系統中，智能傳感器被大量采用[2-3]。所謂多余度智能傳感器，就是在傳統多余度傳感器的基礎上植入微處理器，并使其帶有數據總線通信接口和電源接口，除了具有發送和接收數據這一傳統功能外，還可以執行數據處理、余度管理、故障診斷、故障隔離及故障容錯等功能[4-5]。

目前，傳統的傳感器故障診斷算法已較為成熟，主要包括基于解析模型[6-7]、基于數據驅動[8]和基于知識的方法。近年來，國內外諸多學者將多源信息融合技術應用到故障診斷領域[9]。相比單傳感器，多傳感器的信息融合可以為診斷提供更為豐富的信息，全面反映監控對象的狀態，在某個傳感器失效時正常工作的傳感器可作為冗余備份采集有效的故障信息。李松柏等[10]通過提取多傳感器振動時域信號進行數據級融合，提出了基于信息融合及堆棧降噪自編碼的齒輪故障診斷方法；張明等[9]在融合往復式壓縮機多種類型傳感器采集的特征信息的基礎上，提出一種基于多源信息融合的往復式壓縮機故障診斷方法；錢志勤等[11]提出了基于差分進化的信息融合故障診斷方法，用于變速箱軸承故障診斷；武哲等[12]提出一種基于改進的EEMD譜峭度的多傳感器聯合軸承故障診斷方法，取得了較好的效果。

傳感器故障診斷中最重要的思路是通過冗余信息估計或預測傳感器信號，并與測量值比較產生殘差，然后進行檢測判斷[13]。基于此，本文針對多余度智能傳感器故障診斷問題，提出一種基于數據融合的故障診斷方法。采用經優化的模糊C均值聚類算法融合多傳感器的信息得到融合值，再以融合值作為傳感器信號的估計值，并通過計算各個測量值與融合值之間的殘差來監控傳感器的故障情況。

2 多余度智能傳感器結構原理

多余度智能傳感器結構原理如圖1所示。智能傳感器包括多余度敏感單元、信號調理單元、微處理器及數據、電源總線接口。其工作過程是通過敏感單元獲取被測物理量信號，該信號經信號調理單元預處理后進入微處理器(DSP)，由DSP完成冗余數據的融合處理和自我管理，并完成與中央控制器之間的通信。為提高發動機傳感器的可靠性及測量準確性，航空發動機控制系統中很多傳感器采用了多余度技術。圖1 中，敏感單元1～n既可以在同一位置，也可以分布在不同地理空間。n=1時表示該傳感器是單余度的，n＞1 時表示該傳感器是多余度的。本文主要涉及到n≥3的多余度智能傳感器的故障診斷。

圖1 多余度智能傳感器結構原理Fig.1 The redundancy intelligence sensor structure

3 基于數據融合的多余度智能傳感器故障診斷原理

以某多余度智能溫度傳感器為例，其采用n余度的敏感單元對發動機渦輪后溫度進行測量，并由DSP 對這n個敏感單元進行管理，因此可以考慮采用數據融合技術進行故障自檢測。具體檢測原理如圖2 所示：首先對n個敏感單元的采樣值[T1,T2,T3,…,Tn]進行數據融合，得到一個融合值Tf，然后以Tf作為智能傳感器的輸出并發送到中央控制器，這樣可以保證輸出值具有更高的可信度，提高測量精度；通過對n個傳感器采樣值與Tf的比較得到一組殘差，然后通過殘差決策邏輯對殘差進行決策，得到一組元素為0或1的故障向量，完成傳感器的在線故障檢測與故障定位。

圖2 基于數據融合的多余度智能傳感器故障檢測原理Fig.2 The principle of redundancy intelligence sensor fault diagnosis based on data fusion

本文基于模糊C均值聚類算法[14]對數據進行融合。具體思路是：首先采用模糊C 均值聚類算法將n個采樣序列分為合適的幾個類，類的數量需根據實際傳感器的數目、故障模式確定；然后根據少數服從多數原則，選擇含有最多采樣序列的類的中心作為融合值。類的中心是距離同類中所有向量歐式距離最近的一組向量，因此用其作為融合值合理。

得到Tf后，就可以計算各個敏感單元的采樣值[T1,T2,T3,…,Tn]與Tf的殘差，得到一個殘差向量[e1,e2,e3,…,en]。設定一個故障向量F=[f1,f2,f3,…,fn]用于完成故障分離，故障向量的賦值規則如下：

本文中，閾值的選取由傳感器正常時的殘差序列的均值和標準方差確定，取均值和標準方差的n(1～5)倍之和。設殘差序列的均值為μ，標準方差為σ，則可取故障判定的閾值為ε=μ+nσ。

通過公式(1)就可以得到一個元素為0或1的故障向量F=[f1,f2,f3,…,fn]，通過判斷該故障向量就可以判斷出是多余度智能傳感器的哪一個敏感單元發生了故障。

4 改進的模糊C均值聚類算法

采用模糊C 均值聚類算法可以把n個向量xj(j=1,2,…,n)分為c個組Gi(i=1,2,…,c)，并求每組的聚類中心，使得非相似性指標的價值函數達到最小。選擇歐氏距離為組i中向量xk與相應聚類中心ci間的非相似性指標，則價值函數可定義為：

每一分組都可以用一個c×n的二維矩陣U來表征，矩陣U的元素uij∈[0,1]表示第j個數據xj對組i的隸屬度。根據歸一化規定，一個數據集的隸屬度的和恒等于1。

則式(2)可以變為：

式中：dij=‖xj-ci‖，為第j個數據與第i個聚類中心間的歐氏距離，m∈[1,∞)為加權指數。

構造如下新目標函數：

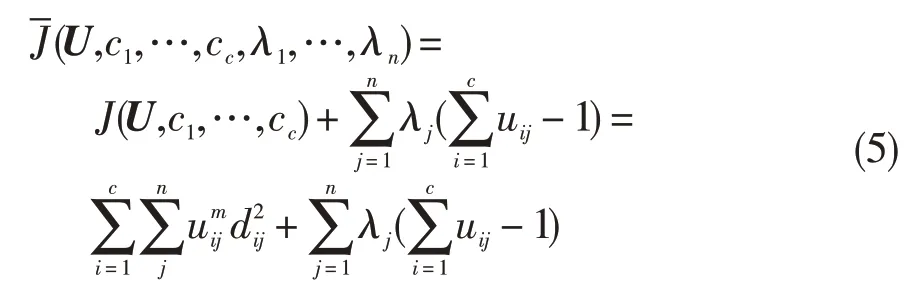
式中：λj(j=1,2,…,n)為拉格朗日乘子。

對輸入參量求導，即得到隸屬度、聚類中心的更新函數：

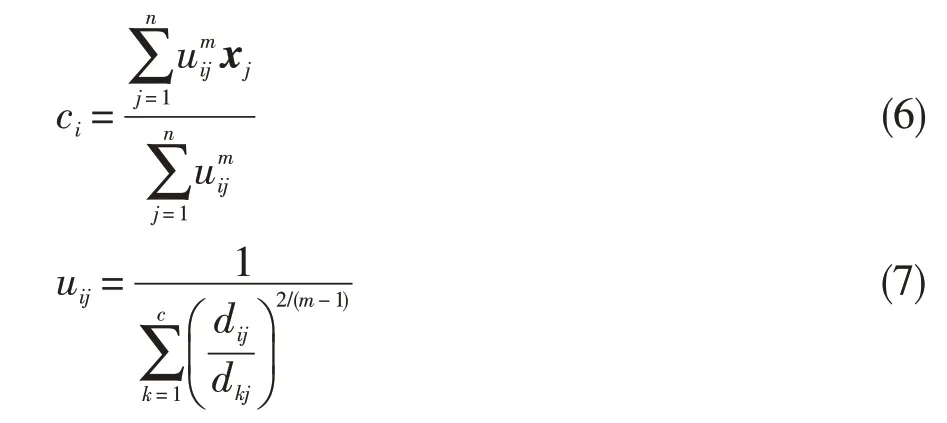
模糊C均值聚類算法的缺點是不能保證收斂于最優解且收斂較慢，算法的性能依賴于初始隸屬度矩陣。若通過尋優方法來確定恰當的初始值，則可以有效克服這一問題。本文采用粒子群算法(PSO算法)[15]對初始值進行尋優來尋求最佳的分類效果。

基本PSO算法可表示如下：假設在D維搜索空間中有m個微粒組成一個微粒群，定義第i個微粒的空間位置為X(i)=(xi1,xi2,…,xid)(i=1,2,…,m)，其所經歷的最優位置為Pi，相應適應度為Fi，飛行速度為vi；所有微粒經歷的最優位置即全局最優位置為Pg，相應適應度為Fg。則第n+1 代微粒第i個粒子的第d維的計算，可根據如下方程迭代：

式中：λ為收縮因子，w為慣性權重，c1、c2為加速系數，rand(1)、rand(2)為兩個在[0，1]之間的隨機數。

初始值尋優的基本思路為：設樣本空間為X={x1,x2,…,xN}，以PSO 中的一個粒子來代表一個隸屬度矩陣U=[uij]c×n，取PSO的適應度函數為

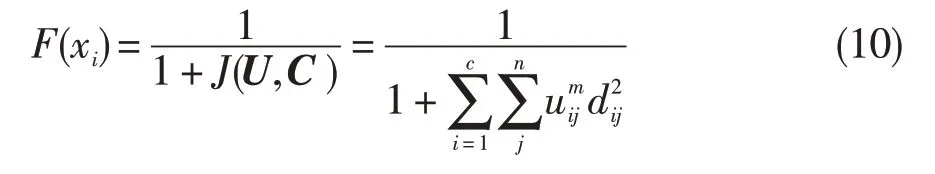
從上式可看出，適應度函數值與分類效果成正比例關系，若分類效果得到改善，J(U,C)將變小，F(xi)將增大。

綜上，經PSO 優化的模糊C 均值聚類算法步驟可表述為：

步驟1 給定聚類數目c，允許誤差ε，設定PSO算法的群體規模m，收縮因子λ，慣性權重w及加速系數c1、c2；

步驟2 初始化粒子群U1,U2,…,Um；

步驟3 根據式(6)計算聚類中心，并根據式(10)計算適應度函數，然后根據式(8)、式(9)產生下一代粒子；

步驟4 若迭代次數達到設定的最大值，則停止迭代，輸出全局最優位置Pg，即最優的隸屬度，否則轉入步驟3；

步驟5 根據式(6)、式(7)更新隸屬度和聚類中心，并計算價值函數，若其相對上次值的改變量小于ε，則迭代停止，否則繼續步驟5。

5 故障檢測仿真

5.1 故障模擬

為保證測量的準確性和可靠性，某渦扇發動機目前共裝有8個傳統熱電偶傳感器來測量渦輪后燃氣溫度。假設未來的渦輪后燃氣溫度智能傳感器也是8余度。，即該智能傳感器共有8個敏感單元來測量渦輪后燃氣溫度，然后由該智能傳感器中的DSP對8 余度的測量值進行數據融合，將融合值發送至中央控制器，完成自身故障檢測與故障定位。

本文以一組真實的發動機渦輪后燃氣溫度數據為藍本，通過一定的數學處理生成8 組渦輪后燃氣溫度，分別代表智能溫度傳感器中8 個敏感單元測得的數據，其中第4、第6 個敏感單元分別發生恒偏差和增益變化故障，其他敏感單元正常，如圖3 所示。具體處理如下：

式中：T1～T8分別為模擬的8 個敏感單元的測量值；x為真實的發動機渦輪后燃氣溫度；ni為隨機數，其均值為0，方差為2；t為時間。

5.2 故障診斷

設定c=3，ε=0.0001，m=50，λ=0.85，w=0.7，c1=1.8，c2=2.2。仿真時，經PSO 優化的模糊C 均值聚類算法將8 組敏感單元測量數據分為(T1,T2,T3,T5,T7,T8)、(T4)、(T6)三類。其中，第一類有6組數據，令該類的聚類中心為Tf，根據少數服從多數原則，將Tf作為智能敏感單元的融合值，如圖4所示。可見，融合值很好地逼近了真實值，絕對誤差小于0.5℃。

計算各個敏感單元測量值與融合值之間的殘差向量[e1,e2,e3,…,e8]，結果如圖5 所示。圖中，線型1代表殘差絕對值，線型2代表閾值。

實際診斷中，閾值需根據發動機實際的渦輪后燃氣溫度計算確定。本節中，可取故障判定的閾值=μ+3σ。由于本節傳感器數據是人工生成，其殘差序列的均值和方差已知，另考慮到實際中渦輪后燃氣溫度場并不均勻，故可適當放寬閾值水平，取=10℃。

確定閾值后，就可以根據各個敏感單元的殘差是否超過閾值得到故障向量。本例中，第4、第6 個敏感單元的殘差超過了閾值，從而得到故障向量為[0 0 0 1 0 1 0 0]。中央控制器通過該故障向量，可以直接判斷出第4和第6個敏感單元發生了故障，從而實現故障定位。

圖3 生成的8個敏感單元測量值Fig.3 The 8 groups of samples generated

圖4 多余度智能傳感器的融合值及其與真實值間的誤差Fig.4 The fusion value and the error between the fusion value and the real value

6 結論

圖5 各個敏感單元的殘差(絕對值)Fig.5 The residual(absolute value)of each sensing unit

提出一種基于數據融合的故障診斷方法，用于航空發動機多余度智能傳感器故障診斷。該方法的總體思路是通過數據融合的手段來估計傳感器信號，并與測量值比較產生殘差作為傳感器故障診斷的依據。其中，在數據融合方面，采用改進的模糊C均值聚類算法對多余度傳感器信息進行分類，選擇含有最多敏感單元測量值的類的中心作為融合值；在故障診斷方面，通過計算各個敏感單元測量值與融合值之間的殘差來診斷傳感器故障，通過故障殘差向量決策邏輯來實現故障傳感器的定位。最后以某型航空發動機8余度渦輪后燃氣溫度智能傳感器為例進行了故障診斷仿真，驗證了數據融合和故障診斷的有效性。