內容整合下的思維發展和認知結構重建

周柳娥

新冠肺炎疫情防控期間的超長寒假“停課不停學”，同一班級的學生雖然學習資源相同，但因為自我管理和學習水平差異，導致學習效果不一。于是，返校后的線上線下教學銜接，成為每一個教師都必須面對和認真解決的問題。我個人認為，“停課不停學”模式下的線上教學特別需要返校后線下教學“以新聯舊、以新帶舊”，借以達到“補有所獲、學有提高”的目的。

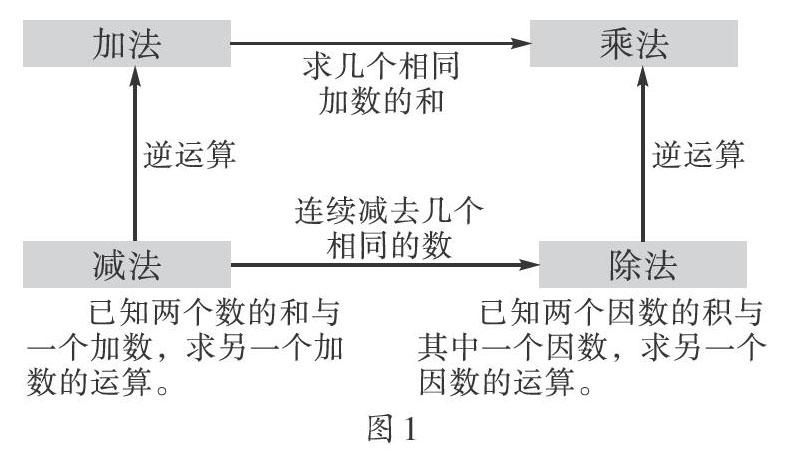
前不久，我上了復學后的第一課——四年級下冊《運算定律》中的“交換律”。我采用“整合+復習串講”的方法，從線上已經教過的《四則運算的意義》開始串講，帶領學生們先復習加、減、乘、除的意義及其關系，歸納出相關的知識結構（如圖1）后，再帶領學生進入加法的交換律探究學習。

新課中的“交換律”探究，依舊沿用整合思維，展開基于數學規律的結構化教學：讓學生先用“猜想規律→舉例驗證→總結規律”的程序探究加法的交換律，再討論乘法、減法、除法運算中是否也存在著“交換律”。

探究“加法的交換律”時，學生通過舉例，一致認定加法中存在著交換律。在學生們正得意時，我提出了下面的問題：“大家列舉的例子都驗證了加法的交換律是存在的，可是，你能列舉出所有的例子嗎？”學生們異口同聲地回答“不可以”。于是我反問學生：“如果沒有辦法列舉出所有的例子，那你們為什么就這么肯定所有的加法都存在著這樣的‘交換律呢？會不會有哪一個加法不存在這樣的規律呢？”幾個學生站起來，大膽地反駁了我，但都是將交換律的含義復述了一遍，而沒有直擊加法交換律的核心本質。……