非規則結構電容層析成像填補法測量的敏感場特性及重構算法改進

陳昭，陳猛，王江江，常家興，劉馬林

（清華大學核能與新能源技術研究院，北京100084）

引 言

電容層析成像法（electrical capacitance tomography, ECT）作為一種多相體系中典型非侵入式測量相含率的方法，在化工流化床[1-4]、石油管道流[5]、顆粒包覆反應器[6]、醫療[7]等領域得到廣泛應用。針對特定應用場合，已開發出適用于煤粉燃燒、石油催化裂化等的高溫測量探頭[8]，圓錐料倉測量的傾斜探頭[9]和Wurster導流管式噴動流化反應器的雙層探頭[10]等。目前測量對象多是規則圓柱[11]、四方[12]或圓臺結構[13]，對于不規則結構中的相含率測量較少涉及。ECT 測量過程包括電極探測、數據采集和圖像重構等步驟，電極板布置不同，其應用場合不同[14]。電極極板覆蓋率影響很大[15]。若電極太長則因“三維弱化效應”，得到的數據不能真實地體現管道軸向上各相介質相含率分布的變化；若電極太短，雖然得到的電容值能很好地反映管道軸向上相含率的變化，但極板長度變小造成測量電容值減小，增加了實際電容測量難度[16]。另外，電極的激發策略也會影響ECT測量和圖像重構的質量[17-18]，因此電極安裝布置和尺寸選擇對于ECT測量非常重要。

針對不規則幾何結構以及所測體系為高溫或強腐蝕性的相含率測量，ECT 電極難以直接布置在管壁上，因此無法實現直接測量。例如由于流化床-化學氣相沉積生產工藝的限制，核燃料包覆顆粒的生產中極易發生孔口沉積現象[19]。為減輕此現象，流化床的入口結構設計為小傾角、自冷卻的多環斜孔式復雜結構[20]。同時由于核燃料顆粒的高密度特性以及核臨界限制，顆粒一次性裝填量較少。因此，核燃料包覆顆粒在流化床中處于淺層、密相、流化高度較低的多孔協同噴動流化狀態。入口處附近的流態化流型分布和顆粒濃度測量對沉積過程研究非常重要，但常規的電極布置無法滿足測量要求。

本文提出通過填補法將復雜結構轉化成規則圓柱結構后進行測量，即將復雜結構的測量問題轉化為規則結構ECT 成像的擬厚壁問題，擴大ECT 的測量范圍。此問題中填充介質的介電常數及填充區形狀可根據需要調整，因此又與一般的厚壁問題不同。有關ECT 的圖像重構算法文獻較多，主要分為線性反投影算法（LBP）、Landweber 迭代算法、Tikhonov 正則化法、更新敏感場矩陣的迭代法等[21-24]。這些方法各有優缺點，需針對填補法進行分析，并發展合適的重構方法。本文首先通過有限元軟件進行填補法測量建模，正向求解填充區敏感場并比較填充區敏感場與標準敏感場特征。然后研究填補法重構成像特征，分別從敏感場特性、歸一化電容、填充區介電常數大小以及圖像重構算法四個方面進行比較分析。進一步基于填補法特性，提出新型圖像重構算法及其優化方向，比較各種算法在填補法重構成像中的重構效果和計算時間，最后給出了本文研究成果在一般性非規則結構中相含率測量中的應用。

1 填補法電容層析成像模型建立

1.1 填補法測量原理

一般非規則幾何結構中，ECT 電容探頭無法直接布置在容器壁上，如圖1（a）所示的測量區。對于一些特殊結構的流化床，例如用于制備核燃料包覆顆粒的小傾角、復雜角度和結構的多環斜孔式流化床，如圖1（b）所示，ECT 測量也受到限制。入口附近的顆粒濃度分布對整個包覆過程十分關鍵，因此ECT 測量面應位于入口處附近，但傳統ECT 電極探頭因尺寸限制，無法直接安裝（150 mm 內徑流化床一般需要50 mm 長的測量電極）。可借鑒數值模擬中為減少計算量，將非結構網格轉換為結構網格的“多重網格法”思想，設置填充區并添加合適的介質，將復雜幾何結構轉化成規則圓柱進行測量。與傳統測量區相比，填補法對應的測量區增加了填充介質區，與結構體增厚類似，但此填充區的介電常數及形狀（一般填充為圓柱，也可以為四方或者圓臺結構）可根據需要改變，可稱為“偽厚壁”問題。

圖1 不規則結構填補法ECT測量一般性原理(a)及填補法應用于多環斜孔式流化床入口處測量示意圖(b)Fig.1 General schematic diagram of ECT measurement of irregular structure with filling method (a)and instrumentation plan of filling method applied to multi-ring slope-hole fluidized bed inlet(b)

1.2 填補法ECT建模

本文建立的填補法ECT 測量模型如圖2（a）所示。測量區為直徑150 mm的圓，測量區內兩相物質的介電常數分別為ε1和ε2，填充區為直徑150～200 mm 的圓環，填充物質的介電常數為ε3，屏蔽層為直徑220 mm 的圓。本文基于有限元軟件COMSOL@進行數值模擬。首先建立12電極的ECT 傳感器模型，接著進行材料屬性設置，設定物理場接地與循環電極激勵等邊界條件[15]，然后進行有限元網格劃分，典型網格劃分如圖2（b）所示。整個傳感器區域劃分為1073 個節點和2064 個三角單元。對敏感場進行計算時提取64×64 的網格數據，其中電極內有效網格點為3228個。

ECT數學模型可簡化為線性方程進行求解

式中，λ 為所有電極對間的歸一化電容值，由高斯散度定理積分求得[23]；S 為歸一化敏感場矩陣，可通過定義法[23]或電場法[25]得到；G為重構圖像中每個像素點位置對應的歸一化介電常數矩陣。為將電容信號轉化成相含率分布圖像，需通過算法進行圖像重構。圖像重構問題是一個欠定問題，不能直接求解敏感場矩陣的逆，需通過迭代或者其他構造算法對真實解進行逼近。電容層析成像算法主要分為迭代算法與非迭代法。迭代算法主要有Landweber 迭代、更新敏感場矩陣的迭代法等，非迭代法有線性反投影算法、奇異值分解法、Tikhonov 正則法[26]等。其中關于經典的Landweber 算法研究較多，從多個角度進行了優化[27-30]。為更精確地比較圖像重構算法的適用性，采用圖像誤差與相關系數進行定量化比較[23]。

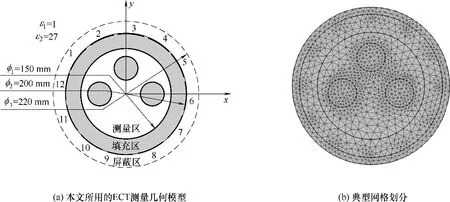
圖2 ECT測量幾何建模及網格劃分Fig.2 Schematic diagram of simplified geometric modeling and mesh generation

2 敏感場比較分析

采取電場法計算敏感場S。敏感場隨著測量截面介電常數分布變化。一般全部填充為低介電常數物質的敏感場為標準敏感場S標。由于激勵邊界條件的周期性和電極分布的對稱性，電極對1-2、1-3、1-4、1-5、1-6與剩余電極的敏感場地圖呈現相同分布。因此列出前5 張敏感場地圖和1-7 對角線敏感場地圖，即可復現單激勵模式下所有電極對的敏感場地圖，如圖3 所示。Ramli 等[31]利用有限元模擬對不同背景下的敏感場進行了圖像重構，其中標準敏感場與圖3（a）類似。

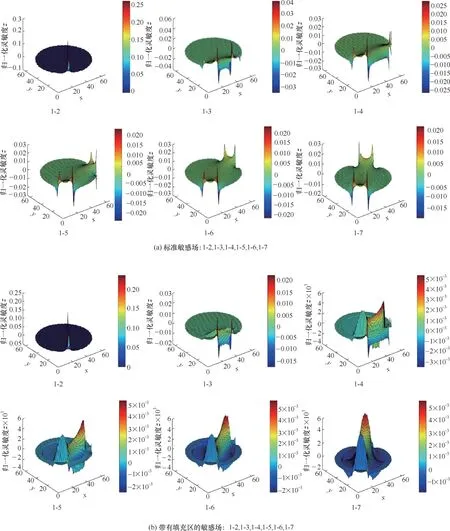
圖3 不同背景下敏感場計算結果對比Fig.3 Comparison of sensitivity map of different background

由圖3 可知，與激勵電極的相對位置不同，敏感場S標呈現不同的變化趨勢。與激勵電極相對位置越遠，敏感場S 的馬鞍形分布越向中心靠近。這說明中心靈敏程度較弱，對電容的反應不靈敏，成像靈敏度差。填充區填滿后，填充區的介電常數增大，利于電場線的傳播，電容絕對值變大，測量信號增強，同時背景信號也增強，因此在帶填充區的敏感場中信噪比降低，即歸一化的標準敏感場的敏感度數量級高于填充區敏感場。在帶填充區的敏感場S填中，相鄰電極敏感場呈現負值，非相鄰電極敏感場地圖中的平臺區開始呈現非對稱趨勢，這是因為填充介質導致信號增強，抬升了靈敏度。

3 填補法ECT 重構成像影響因素研究

在填補法中，填充區的介電常數分布ε填可作為已知的邊界條件來優化重構成像。為提高填補法下的成像質量，本文擬從敏感場、歸一化電容值及圖像重構算法三個方面對圖像重構進行探究，如表1 所示。另外還對填充區介電常數ε填的影響進行了分析。

表1 本文研究案例定義Table 1 Case definition in this study

3.1 不同背景敏感場的影響

由圖3 知，S填與S標呈現相似的馬鞍形變化，均表現為中間低四周高的敏感度趨勢。S填的敏感度數量級與S標不同。為探究敏感場特性對圖像重構質量的影響，對1-a-乙、2-a-乙、3-a-乙的圖像進行比較。分別計算了半管流、核心流與環狀流的圖像誤差與相關系數，結果如圖4所示。

由圖4 可知，1-a-乙與3-a-乙結果接近，2-a-乙與前兩者在半管流與核心流的重構上差異不大，但在環狀流的重構上差異十分明顯，且2-a-乙環狀流成像質量增強。這表明，本案例中的S填對環狀流有增強成像的趨勢。總體而言，不同敏感場對成像的影響差別不大。文獻[31]指出，基于空背景的通用敏感場適用于大多數圖像的重構，與本文結論類似。因敏感場2 能加強環狀流成像，因此選擇此敏感場作為后續探究的前提條件。

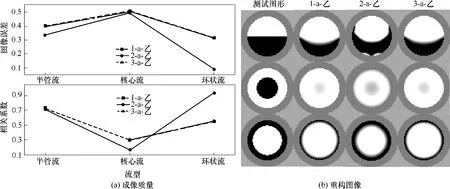
圖4 不同敏感場下成像質量和重構圖像Fig.4 Imaging quality and reconstruction images under different sensitivity maps

3.2 歸一化電容值影響

歸一化電容的目的是消除噪聲對圖像重構的影響。在填補法問題中，人為引入的填補區也是一種噪聲信號。因此可通過幾何建模時考慮填充區計算出電容，然后在電容歸一化時去除填充區結構噪聲的影響。為探究歸一化電容對成像的影響，對2-a-乙、2-b-乙的圖像進行比較，如圖5所示。可以看出，2-b-乙中所有流型的成像效果均略優于2-a-乙。這表明在進行電容歸一化時，去除填充區結構噪聲有利于提高圖像重構質量。

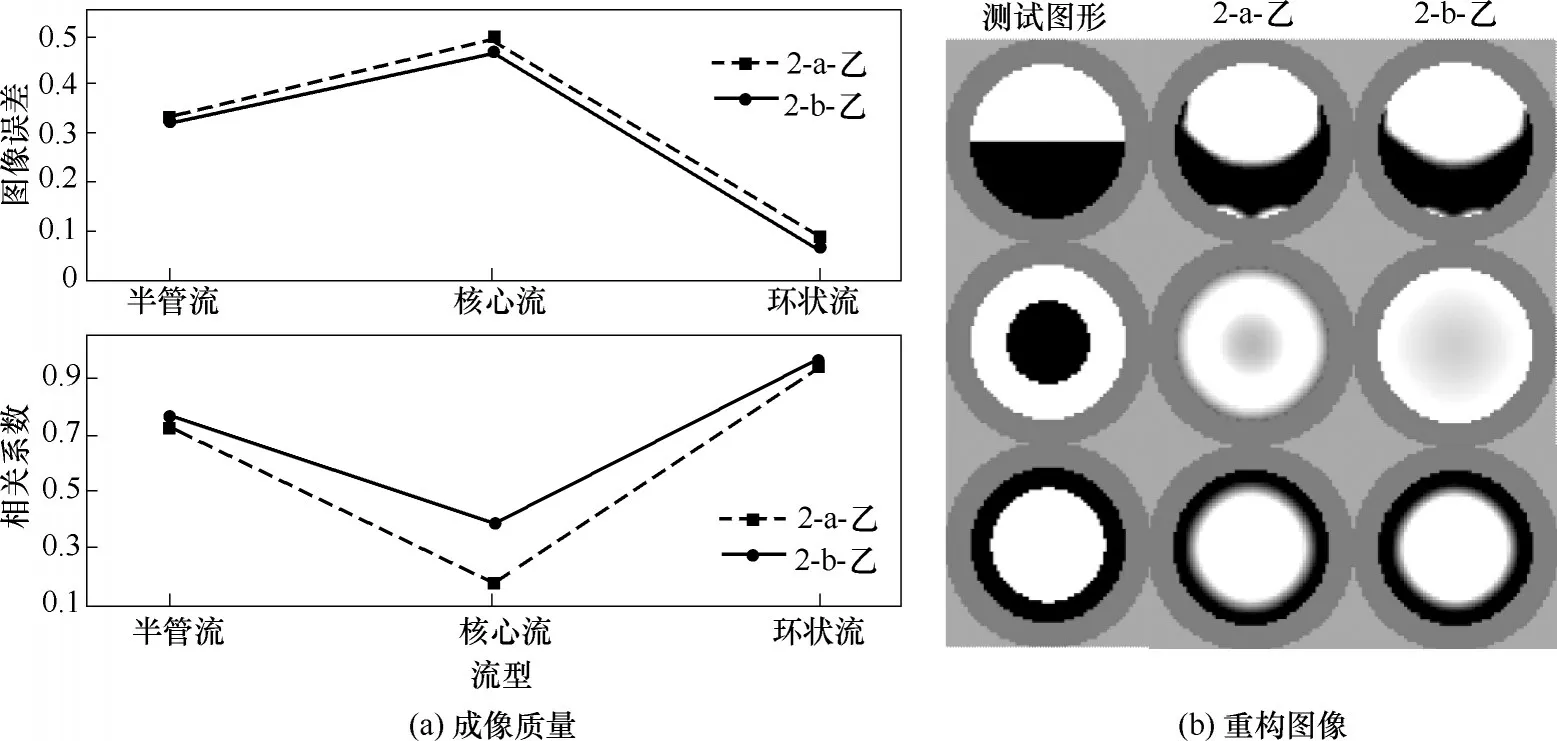
圖5 不同歸一化電容下成像質量和重構圖像Fig.5 Imaging quality and reconstruction images under different normalized capacitance

3.3 填充區介電常數對成像的影響規律

填充區介電常數ε填的分布會影響整個測量區的電勢分布。對ε填的影響規律進行探究，選擇填充合適的介質使其成像最佳，具有重要意義。模型中測量物體的介電常數ε測量體為27，空氣介電常數為1，對ε填進行梯度模擬實驗，結果如圖6 所示。不論半管流還是核心流，當ε填與ε測量體相同時，重構圖像表現最佳的成像質量，因此在采用填補法電容層析成像方法測量相含率時，ε填應與測量區中較高的ε測量體相近或者一致。

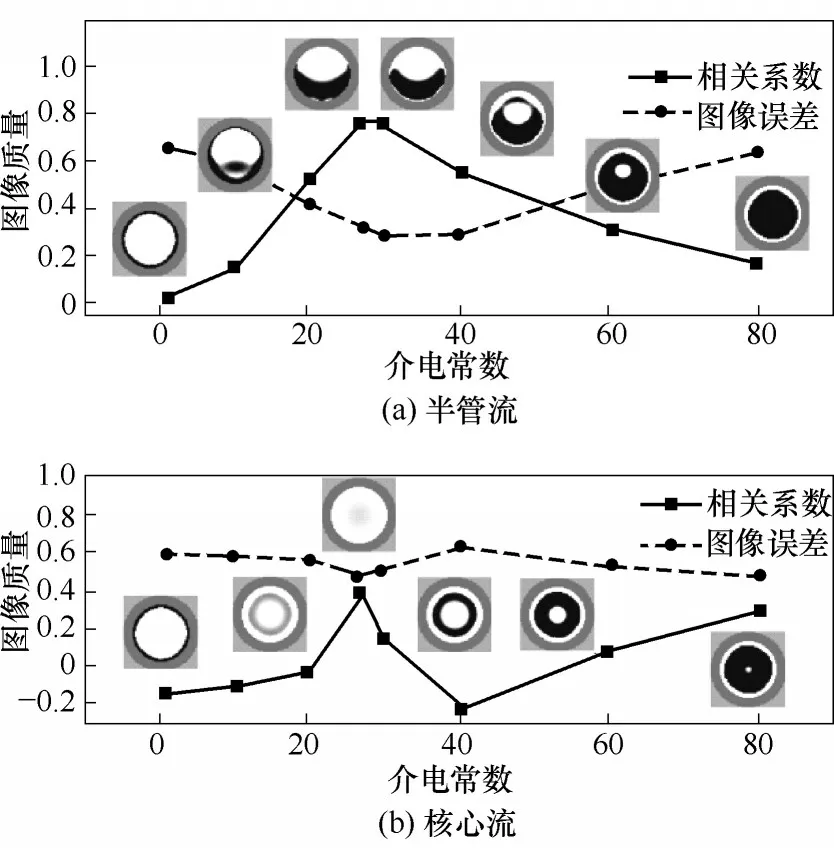
圖6 半管流和核心流在不同填充區介電常數下的圖像重構效果Fig.6 Reconstruction images of half-tube flow and core flow with different permittivity in filling area

3.4 填補法圖像重構算法改進

填補法測量時，填充區會占據電容信號的一定比例，導致真正的成像信號較弱。但填充區介電常數分布已知且可調，因此可通過固定或去除填充區信號的方式減少求解的維度，從而改善圖像重構質量。據此，本文提出兩種改進思路，即變換矩陣和拆分矩陣的Landweber 算法。前者在算法迭代過程中固定填充區介電常數矩陣，后者在迭代前在重構方程中把填充區分離。

對于本文幾何模型和網格劃分，ECT 測量模型為

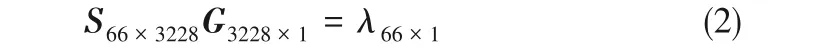
矩陣的形式表達如下

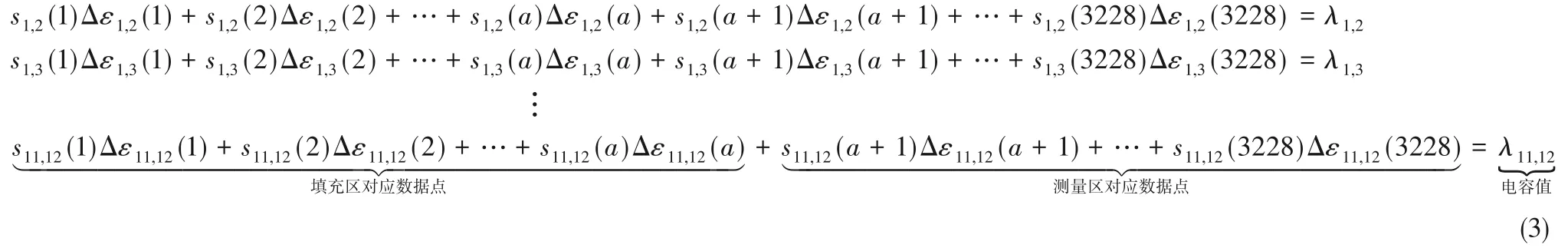
Δε(k)理論上是對應標準圖像(0,1)間的排布，即歸一化介電常數矩陣，反映的是圖像像素分布。

3.4.1 基于變換矩陣改進的Landweber 算法 建立變換矩陣P1、P2，將ε填與測量區的介電常數ε測量區對應的矩陣分離。ε填矩陣作為已知條件在Landweber迭代中保持不變，ε測量區矩陣則隨迭代過程逐漸靠近真實解。

如式(4)所示，P1代表填充區區域，P2代表測量區域。P1、P2分別為與填充區排列點位置、測量區排列點位置相同者為1，其余位置為0的列向量作為對角陣的矩陣，維度為3228×3228。

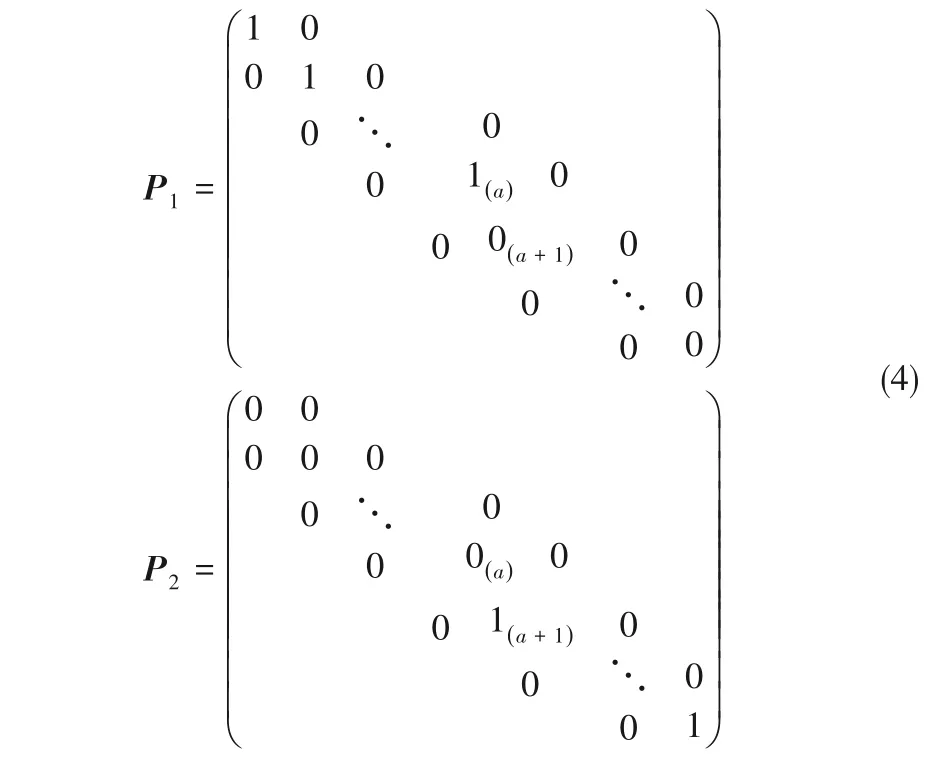
由式(3)可知

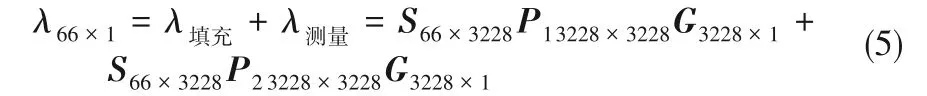
變換矩陣的Landweber算法推導如下

保持填充區部分不變

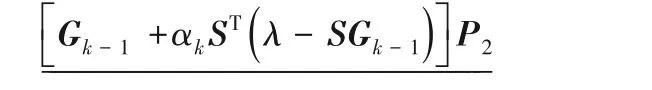
測量區部分進行迭代

令填充區

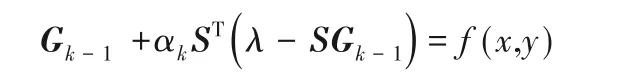
其中，f(x,y)為與填充區位置相關的介電常數分布函數。ε填已知，將其代入歸一化電容計算公式中，理論上可得f(x,y) = I，I 為單位矩陣。考慮到填充區全為單位矩陣時，迭代限制較為嚴格，會降低測量區的重構質量，則f(x,y) = H,H 為在Landweber算法下填充區作為測量成像的介電常數矩陣。此時，帶有填充區的成像可以看作填充區與測量區待測形狀的復合成像。ε填的分布會直接影響到待測圖形的重構，因此在固定填充區時，需考慮填充區與測量區之間的相互關系，引入松弛因子調節兩者的相互作用

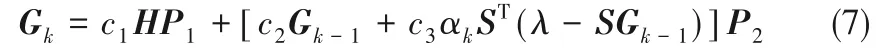
其中，c1、c2、c3為松弛因子。以上為變換矩陣改進的Landweber 算法。此算法是在固定填充區矩陣的前提下進行搜索的，f(x,y)的選擇影響較大。各表達式重構結果如圖7 所示。通過松弛因子調節后，半管流重構效果良好，核心流重構效果較弱，此方法中的松弛因子與重構的關系值得進一步研究。

圖7 不同函數下的變換矩陣重構結果Fig.7 Reconstruction results of transformation matrix with different functions

3.4.2 拆分矩陣改進的Landweber算法 由于ε填分布已知，在圖像重構中可預先將其去除，以減少不適定問題的未知數個數，降低填充區帶來的非線性影響，提高重構精度。由式（3）可知

因此，可通過拆分ε填矩陣與ε測量區矩陣重新構造求解公式，以降低求解的維度。

其中，a 表示填充區數據點的個數，S1表示填充區對應的敏感場，S2表示測量區對應的敏感場，G1表示ε填分布，G2表示ε測量區分布，b 表示去除填充區引起的電容變化值后的電容值，即僅由測量區物體引起的電容變化值。式（8）和式（9）即為拆分矩陣的Landweber重構算法。

3.4.3 圖像重建結果比較 LBP、Landweber 迭代算法與Tikhonov正則化算法是目前ECT圖像重構中應用廣泛的算法。為探究不同算法在填充條件下的作用效果，對以上三種算法與變換矩陣改進的Landweber 算法、拆分矩陣處理的Landweber 算法結果進行對比，即2-b-甲，乙，丙，丁，戊。圖8 是進行重構比較的圖形結果，同時統計出了各算法重構所需要的時間，如表2所示。

圖8中白色表示空氣，黑色表示流體，灰色表示填充區。用上述算法分別對半管流、核心流、環狀流、雙管流和三管流進行圖像重構。對于半管流，普遍存在不同程度的凹陷變形，變換矩陣-Landweber 方法一定程度上抑制了這種變形。對于核心流，重構效果普遍偏弱，這是敏感場的敏感度邊壁強、中心弱的特性導致中心信號變化不強造成的。變換矩陣針對半管流成像效果較好。拆分矩陣在一定程度上增強了中心信號的顯像，邊緣較其他圖像銳化。對于環狀流，Landweber 算法與拆分矩陣-Landweber 方法重構質量較好。但是對于雙管流和三管流復雜的流型，僅Landweber 算法、Tikhonov 算法和拆分矩陣算法能夠重構有效圖像，其中基于拆分矩陣算法的Landweber 算法重構質量較優。

圖8 不同算法針對填補法成像的結果Fig.8 Results of different algorithms for thick wall imaging

圖9 和圖10 分別為以上算法的圖像誤差與相關系數的比較。由圖可知，變換矩陣法在半管流的成像中圖像誤差最小，相關系數最大，優于其他算法。而在環狀流的成像中，Landweber 算法與Tikhonov 算法成像較優。而拆分矩陣算法在以上流型的重構中處于中間效果，但圖像成像清晰，失真程度在可接受范圍內。針對復雜的雙管流和三管流，Landweber 算法與拆分矩陣算法表現較優。綜合比較計算時間（表2）和成像質量，基于拆分矩陣算法的Landweber 算法是一種最佳選擇。接下來對此算法進行進一步優化研究。

表2 各重構算法的計算所需要的運行時間Table 2 Running time of each reconstruction algorithm

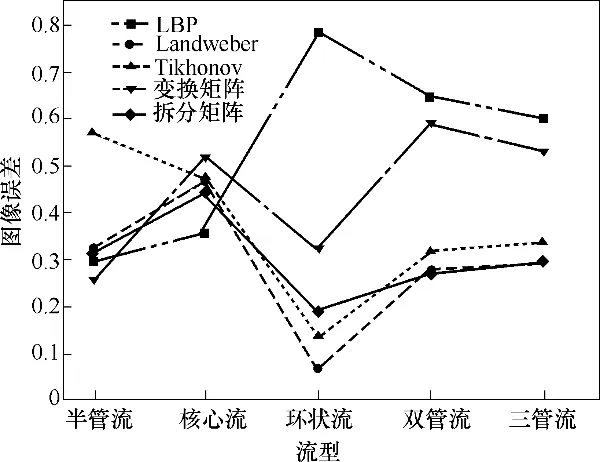
圖9 不同算法的圖像誤差Fig.9 Image error of different algorithms

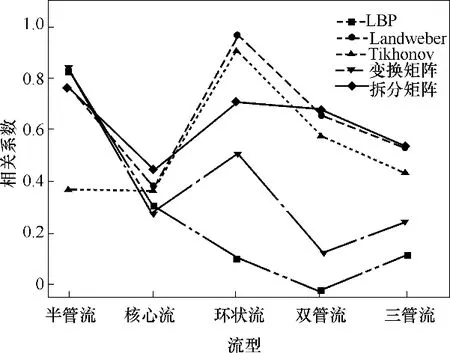
圖10 不同算法的相關系數Fig.10 Correlation coefficient of different algorithms

3.4.4 拆分矩陣算法的優化策略 在Landweber 算法中，選擇合適的α 才能獲得較為逼近的成像效果[32]，類似地，可采用添加合適的松弛因子，改變搜索方向的步長來優化拆分矩陣法。

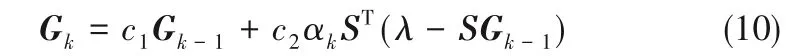
其中，c1和c2為松弛因子。c2控制最速下降方向上的步長長度，可用來改變圖形分化的程度。c1控制原圖保留的程度，調節c1值即調節原圖的占比來彌補搜索方向上圖形的失真。圖11（a）為不同c1下用拆分矩陣法對半管流進行重構的圖像。隨著c1的增加，圖像重構質量先變優后下降，即存在一個c1值使圖像重構質量最佳。圖11（b）為不同c2下用拆分矩陣法對雙管流進行重構的圖像。c2越大，圖像越銳化，成像部分面積越小。這說明c2的物理意義是通過犧牲成像面積來增強圖像清晰程度的。針對未知的流型，可先進行一系列的預實驗，判斷流型大致趨勢，經過測試，可以給出同類型流型（如層流、環狀流、氣泡流等）的c1和c2的值，供實際測量時參考使用。圖11（c）給出圖8 中三管流成像在推薦參數下的優化成像。

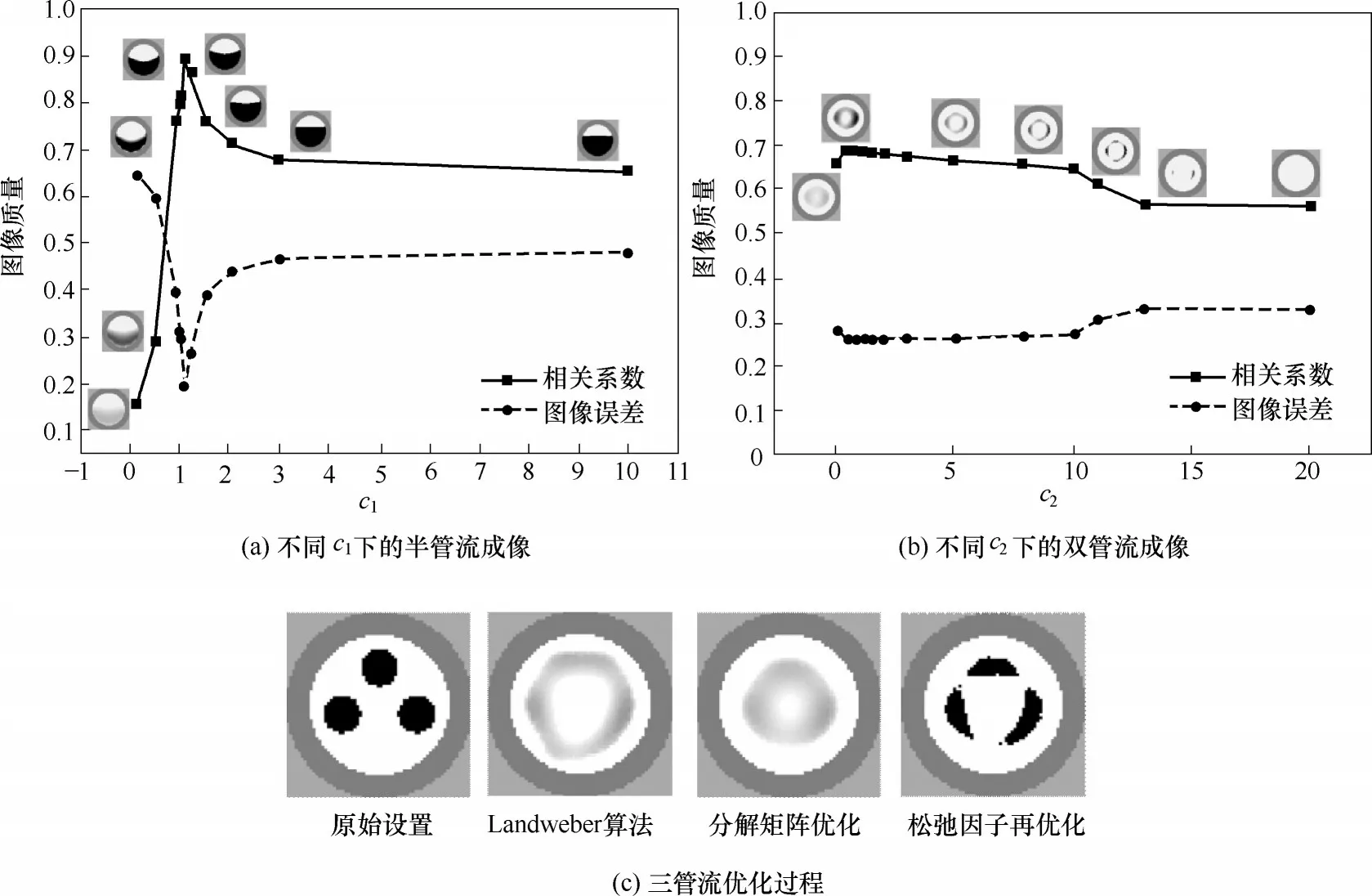
圖11 不同c1下的半管流成像、不同c2下的雙管流成像及三管流優化過程Fig.11 Half-tube flow at different c1,double tube flow at different c2 and optimization of triple tube flow

4 一般非規則結構的填補法測量ECT技術應用

填補法可應用于ECT 探測在復雜結構或苛刻環境等不適宜直接在反應器壁上安裝電極的情況。采用一般非規則結構，對上述填補法測量算法進行驗證。選擇：①填充區敏感場（填充區形狀非規則）；②去填充區噪聲的歸一化電容值；③填充介質介電常數和測量區高介電常數一致；④基于拆分矩陣和松弛因子改進的Landweber 重構算法，對非規則結構進行不同高度層流下的圖像重構。結果如圖12 所示。由圖可知，對淺層流、半管流和近滿管流的圖形重構精度較好。圖像相關系數90%左右，重構時間在毫秒級，可滿足一般化工過程測量及流動檢測要求。

圖12 針對非規則結構的填補法下的圖像重構結果和圖像重構評價指標Fig.12 Image reconstruction based on filling method for irregular structure and evaluation of image reconstruction

5 結 論

本文提出填補法ECT 技術用于測量不規則結構中的兩相體系相含率。文中首先對ECT 敏感場特性進行比較，然后詳細研究了不同背景的敏感場強度、歸一化電容值矩陣、填充區介電常數大小以及圖像重構算法對重構圖像的影響，并提出了改進重構算法，優化了圖像重構質量。總結上述研究，得出主要結論如下。

（1）填補法會增加敏感度，電容信號絕對值增強，非線性程度增加，信噪比降低。不同背景的敏感場對電容層析成像影響不大，但填充區敏感場可強化環狀流成像。

（2）去除填充區結構噪聲的電容值歸一化處理有利于提高圖像重構質量。

（3）當填充區介電常數與待測區兩相中高介電常數一致時，圖像成像質量最佳。

（4）變換矩陣法與拆分矩陣法均可在一定流型下改善成像。對于半管流，變換矩陣成像最優，但具有方向性，值得進一步深入優化研究；對于各種流型，綜合計算速度和成像質量，拆分矩陣法是填補法成像的最優選擇，并可通過選擇松弛因子使重構圖像更加準確。對同類型的流型可給出先驗性的松弛因子提高成像質量。

（5）本文提出測量建議：采用填充區敏感場，采用去填充區噪聲的歸一化電容值，填充介質介電常數和測量區高介電常數一致，基于拆分矩陣和松弛因子改進的Landweber 重構算法，可用于不規則結構相含率測量中，還可用于因高溫、腐蝕等無法直接進行電極安裝的工業場合中，具有改進多相流測量方法的普遍意義。

致謝：感謝中國科學院工程熱物理研究所王海剛研究員和英國曼徹斯頓大學楊五強教授在本文涉及的電容層析成像算法研究方面的幫助。

符 號 說 明

a——填充區單元數

b——剔除填充區引起的電容變化值后的歸一化電容值

c1,c2,c3——變換矩陣和拆分矩陣的松弛因子

G,G1,G2——分別為歸一化真實圖像介電常數矩陣，拆分后的厚壁區、測量區歸一化介電常數分布矩陣

H——在Landweber 算法下填充區作為測量成像的歸一化介電常數矩陣

I——單位矩陣

P1,P2——分別為厚壁區、測量區對應的變換矩陣

S,S1,S2,S標,S填——分別為歸一化敏感場矩陣，拆分后的厚壁區、測量區歸一化敏感場矩陣，標準敏感場，帶有填充區的敏感場

αk——Landweber算法里的松弛因子

ε0,εr,ε1,ε2,ε3,ε填,

ε測量區,ε測量體——分別為真空介電常數，傳感器截面的介電常數分布，模型中測量區低介電常數，模型中測量區高介電常數，模型填充區物質的介電常數，泛指填充區介電常數變量，泛指測量區所有介電常數分布，泛指測量區中的測量物體的介電常數，C2/(N·m2)

λ——電極對歸一化電容值

下角標

k——迭代次數