基于數(shù)據(jù)挖掘聚類算法的網絡學習平臺學生成績分析
肖自乾 陳經優(yōu)


摘要:目前越來越多的教師選擇“互聯(lián)網+”線上線下相結合的模式開展教學活動,如何利用信息化技術進一步優(yōu)化學情分析以提高教學質量是我們需要面對的問題。文章以智慧樹在線教學平臺學生平時各方面表現(xiàn)數(shù)據(jù)為研究基礎,通過大數(shù)據(jù)聚類分析對學生進行分類,直觀呈現(xiàn)不同學生群體特點,便于教師有針對性地提出相應教學策略。
關鍵詞:智慧樹;聚類;K-均值;可視化;離散點
中圖分類號:TP301 文獻標識碼:A
文章編號:1009-3044(2020)19-0028-02
開放科學(資源服務)標識碼(OSID):
1 引言
隨著信息技術的發(fā)展,教學模式的不斷改革創(chuàng)新,越來越多的教師選擇“互聯(lián)網+”線上線下相結合的教學模式。目前市場上涌現(xiàn)出眾多網絡課程互動平臺,相關企業(yè)機構也在積極探索不斷優(yōu)化線上線下的教學設計。本文以智慧樹在線教學平臺學生平時各方面表現(xiàn)數(shù)據(jù)為研究基礎,通過大數(shù)據(jù)聚類分析對學生進行分類,呈現(xiàn)不同學生群體特點,便于教師有針對性地提出相應教學策略,從而優(yōu)化教學方式方法,提升教學效果。
2 聚類分析算法
聚類是統(tǒng)計數(shù)據(jù)分析的一門技術,在許多領域受到廣泛應用,包括機器學習,數(shù)據(jù)挖掘,模式識別,圖像分析以及生物信息。聚類是把相似的對象通過靜態(tài)分類的方法分成不同的簇或者更多的子集,同一個簇或子集中的所有對象都有相似的特點或屬性[1]。
2.1 K-均值算法
K-均值算法是在信號處理中常使用的一種向量量化方法,目前在數(shù)據(jù)挖掘等領域應用較為廣泛,如游客客戶分類等應用場景。它是一種基于相似性的無監(jiān)督學習算法,在判定兩個樣本相似性時通常需要定義一個距離函數(shù)。K-均值算法的目標是將把n個點劃分到k個簇中,使得每個點都屬于離他最近的均值(此即簇的質心)對應的簇,每個簇的中心是通過計算簇中所含值的均值得到的,并以之作為聚類的標準[2]。
2.2 本課題數(shù)據(jù)分析流程
本課題研究中,首先我們應用肘部法則對數(shù)據(jù)進行分析,得到不同k值時的平均畸變程度,一般我們會選擇平均畸變程度最大的k值進行聚類分析;然后是根據(jù)得到的k值進行聚類分析,在這里我們使用的是MachineLearning開源庫中的KMeans算法,算法流程在這里就不再詳細闡述;緊接著我們將聚類得到的數(shù)據(jù)進行降維處理,并可視化呈現(xiàn),同時我們還對離群點進行統(tǒng)計,以便于我們對數(shù)據(jù)做更全面的分析;最后是根據(jù)得到的各簇質心繪制雷達圖.呈現(xiàn)不同學生類別的表現(xiàn)情況。
3 網絡學習平臺學生數(shù)據(jù)
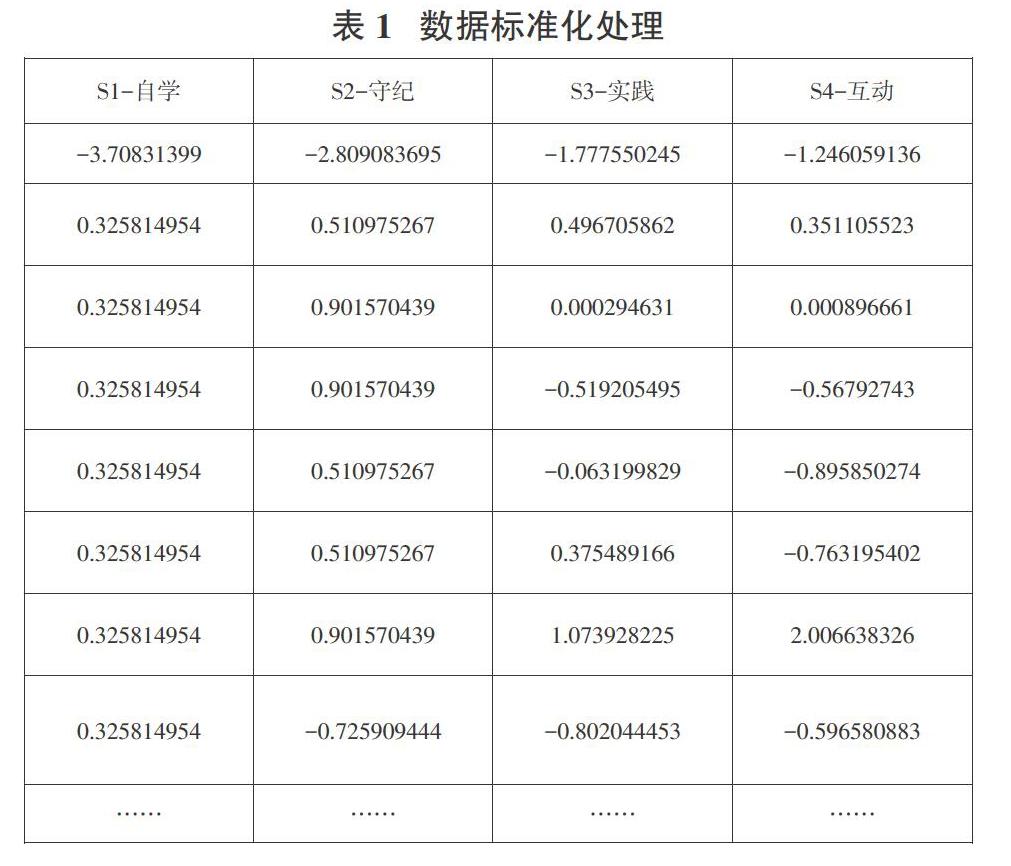
智慧樹平臺中導出的平時成績由視頻資源學習、非視頻資源學習、簽到、測試、討論答疑、頭腦風暴、投票問卷、作業(yè)/小組任務、課堂表現(xiàn)、被老師點贊加分等構成,加權比例可根據(jù)實際情況進行調整。現(xiàn)將成績項分為四部分,即:自學、守紀、實踐以及互動,本文的數(shù)據(jù)分析將圍繞這四個維度進行[3]。為避免每個指標數(shù)據(jù)取值范圍差異過大的問題,需要進行數(shù)據(jù)標準化處理,得到成績表如下:
4 數(shù)據(jù)分析及結論
4.1 確定k值
根據(jù)肘部法則對學生成績數(shù)據(jù)進行分析,計算不同k值時的平均畸變程度,如圖1所示。
從圖1可以看出,隨著k值的變化平均畸變程度也在不斷變化,在當前的樣本數(shù)據(jù)分析中當k值為3時,平均畸變程度最大,因此我們用k值為3進行聚類分析。
4.2 聚類結果可視化
選取k值為3時聚類結果可視化如圖2所示,聚類分析數(shù)據(jù)結果見表2聚類分析后數(shù)據(jù)。
4.3 雷達圖展示
雷達圖是以從同一點開始的軸上表示的三個或更多個定量變量的二維圖表的形式顯示多變量數(shù)據(jù)的圖形方法。雷達圖主要應用于企業(yè)經營狀況——收益性、生產性、流動性、安全性和成長性的評價[4]。各類學生雷達圖呈現(xiàn)如圖3所示。
4.4 離群點分析
本課題研究采用基于距離的離群點檢測,這些離群點往往代表學生可能具有比較特殊的特點,因此我們需要對這些情況進行詳細分析[5]。離群點分析如圖4所示。
4.5 結果分析
首先從聚類結果來看,“0”類學生在雷達圖中顯示最為全面,各方面表現(xiàn)均較為良好;“1”類學生在實踐和互動兩方面表現(xiàn)差強人意;“2”類學生則各方面表現(xiàn)均較差,特別是在自學方面。其次從離群點分析來看,3個離群點均屬“1”類學生,通過對比發(fā)現(xiàn),其中一個學生在自學、實踐以及互動方面均較差,但在守紀方面做得較好,其他2位學生在四個方面的表現(xiàn)非常不均衡,但同時也存在很大的提高潛力,教師在教學過程中多加關注、指導將會有很大進步。
5 結語
本課題通過對學生平時表現(xiàn)數(shù)據(jù)進行聚類分析,將具備相似特點的學生聚成一類,教師則可以通過特點分析找出適合的教育教學方法,逐步促進學生各方面的改進和提高,同時對于一些具備特定特點的學生則可以更加明確的掌握,以便幫助其逐步改進。
參考文獻:
[1]王川,張珍文,安帥,聚類支持下決策樹模型在動車組空調故障檢測中的應用[J].中國新技術新產品,2018(13):15-16.
[2]張興強.基于快速局部均值估計的噪聲水平估計算法及其應用研究[D].南昌大學,2017.
[3]楊洪琴,楊輝.大數(shù)據(jù)視域下大學生移動學習探究——基于智慧樹平臺的公選課應用分析[J].四川職業(yè)技術學院學報,2019,29(03):115-122.
[4]劉香榮.基于HMM的管道安全監(jiān)測DAS信號時序信息挖掘與識別方法[D].電子科技大學,2019.
[5]鄧玉潔,基于聚類的離群點分析方法研究[D].重慶大學,2012.
【通聯(lián)編輯:王力】
基金項目:海南省教育廳科學研究項目:K-means聚類算法在旅游業(yè)游客細分中的應用研究(Hnky2016-66);海南自然科學基金項目:基于MapReduce的改進樸素貝葉斯算法在社交網絡數(shù)據(jù)挖掘中的研究及應用(618MS078)
作者簡介:肖自乾(1982-),男,四川省自貢市人,碩士,海南軟件職業(yè)技術學院副教授,主要研究方向為算法設計、大數(shù)據(jù)技術;陳經優(yōu)(1983-),女,海南省東方市人,碩士,海南軟件職業(yè)技術學院副教授,主要研究方向為算法設計、軟件設計。

