DBSCAN聚類處理的改進蟻群算法在車輛路徑問題中的應用

徐書揚 俞鴻烽 潘華錚 張宇來

摘要：傳統的蟻群算法在求解車輛路徑問題時迭代速度較慢，且求解精度較低，易陷入局部最優。針對這些問題，利用DB-SCAN聚類算法對車輛路徑問題中的各個物料配送點進行聚類劃分，并根據聚類劃分的情況對蟻群算法中的信息素矩陣合理初始化，實現對蟻群算法的改進，使得改進后的蟻群算法能有更高的求解精度和更快的收斂速度。通過MAT-LAB2019A對實驗結果進行仿真測試，并與其他算法橫向對比，可得改進后的蟻群算法在求解輛路徑問題時有著更高的求解精度和更快的收斂速度，特別是在配送點分布相對密集和各配送點需求量較小時有著明顯的效果。

關鍵詞：蟻群算法;DBSCAN聚類算法;車輛路徑問題

中圖分類號：TP391 文獻標識碼：A

文章編號：1009-3044（2020）19-0182-05

開放科學（資源服務）標識碼cOSID）：

1 概述

隨著互聯網科技的不斷完善，人們越來越多的選擇通過網上購物來滿足自己的購買需求。因此合理的物流方案設計，也成為物流配送中的難點與焦點。早在1959年，Dantzig和Rems-er提出了車輛路徑問題（Vehicle Routine Problem）[1]，將復雜的物流問題抽象成了圖論問題供學者研究，該問題的優化目標為貨車在載重有限的情況下如何規劃路徑使得完成貨物配送所經過的路程長度最短。VRP問題屬于NP問題，隨著所要配送的點數增多，用精確算法求解會導致計算量過大，因此精確算法求解VRP問題并不適用。1986年，Solomon首次提出用啟發式算法來求解VRP問題[2]，研究發現，啟發式算法能在保證一定的求解精度的情況下有著較小的算法復雜度，因此更適用于VRP問題的求解。1999年，Dorigo和Gamberdella首次提出利用啟發式算法中的一種：蟻群算法來求解VRP問題[3-4]，由于蟻群算法本身具有良好的魯棒性和較高的求解精度，國內外學者開始嘗試利用改進的蟻群算法或是相關的混合算法來求解VRP問題，例如，趙群在文獻[5]中提出利用蟻群算法和遺傳算法的混合算法求解VRP問題;劉春英在文獻[6]中提出利用粒子群算法和蟻群算法的混合算法求解VRP問題;石華踽在文獻[7]中將車輛轉移規則應用到算法中使算法具有更強的應用;鄭文艷在文獻[8]中更改了信息素更新方式和可行解構造以提高算法的求解精度。

此外Dhawan C.Kumar Nassa V在文獻[9]中總結了前人的研究，在蟻群算法解決VRP問題上做了總結，比對了各代改進算法的優缺點，為今后的研究做了導向。M artin等人對DB-SCAN算法進行了簡單的闡述[10]，該算法能在具有噪聲的空間數據庫中發現任意形狀的簇，可將密度足夠大的相鄰區域連接，能有效處理異常數據，主要用于對空間數據的聚類。作為一種知名的聚類算法，BDSCAN算法廣泛地應用于各個領域，例如無線電技術[11]，復雜環境監測[12]屏常數據處理[13]等.在物流管理問題中也有著應用，張洪奉在文獻[14]中提出了利用BDSCAN算法的改進算法來設計物流信息管理系統。前人對于蟻群算法求解VRP問題的改進有著明顯的效果，但是都未考慮到信息素矩陣的合理初始化對于算法收斂的導向作用。本文對傳統的蟻群算法進行改進，通過BDSCAN算法將VRP問題中的各個物料配送點進行劃分聚類，并以此作為信息素矩陣初始化的依據，使得初始信息素矩陣對算法的收斂有導向作用，讓算法有著更高的求解精度和更快的收斂速度。

2 背景知識和算法描述

2.1 VRP問題

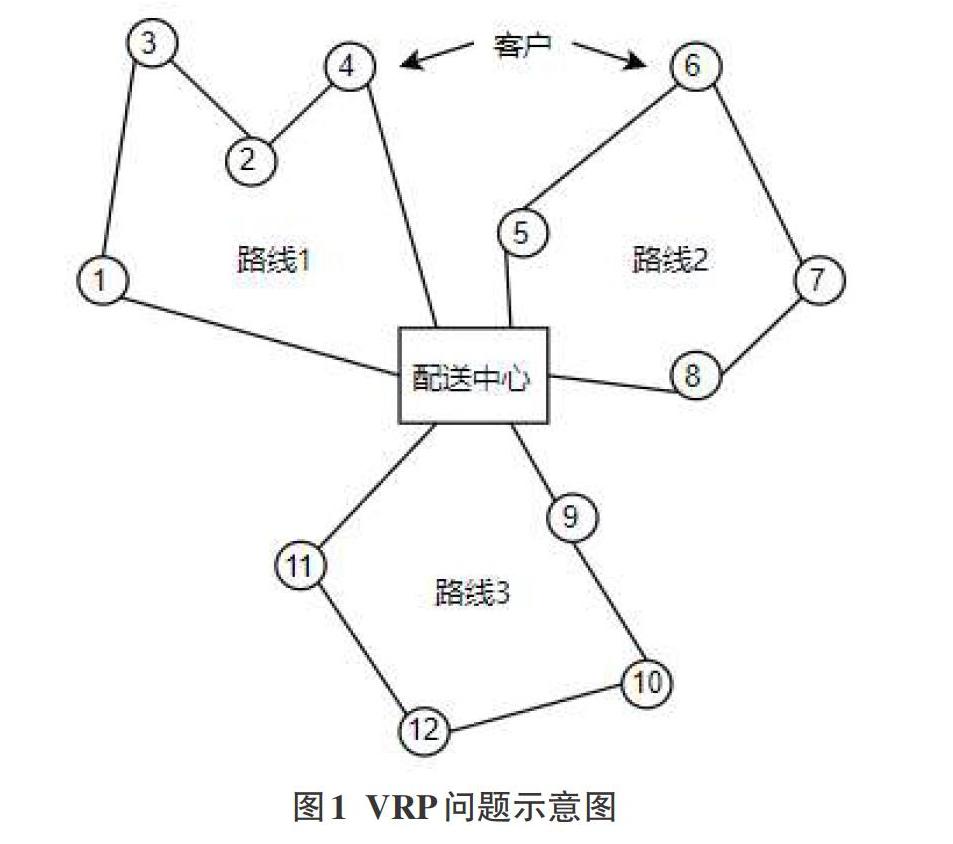
Dantzig和Remser提出了車輛路徑問題（Vehicle RoutineProblem，簡稱VRP），它是運籌學重要的研究問題之一。VRP問題關注一個供貨商與k個銷售點的路徑規劃的情況。該問題可以簡述為：給定配送中心、一個車輛集合和一個顧客集合，車輛運載能力和顧客需求量已知，每輛車都從配送中心出發，完成運送任務后重新返回配送中心，目標是在特定的約束條件下滿足客戶需求并且使得成本最小化，配送訂單最大化，滿載率最大化。圖形表示如下：

2.2 蟻群算法

蟻群算法（Ant Colony Algorithm，AC）由Dorigo和Gam-berdella首次提出，該算法能夠模擬自然界中螞蟻的覓食行為。昆蟲學家們發現螞蟻在行走過程中能夠釋放用來標識自己行走路徑的稱為“信息素”的物質，路徑長遠可以通過信息素濃度大小表示，信息素濃度越高，對應的路徑越短。該算法的其基本思路為：將螞蟻的行走路徑作為待優化問題的可行解，整個螞蟻群體的所有路徑構成待優化問題的解空間。路徑較短的螞蟻所釋放的信息素量較多，隨著時間的推進，較短的路徑上累積的信息素濃度逐漸提高，選擇該路徑的螞蟻也隨之越來越多。最終，整個螞蟻群體通過信息素交換路徑信息在正反饋的作用下集中到最佳路徑上，該路徑對應的就是待優化問題的最優解。

蟻群算法流程如下：

（1）初始化參數

對相關參數進行初始化，如螞蟻數量m、信息素重要程度因子a、啟發函數重要程度因子6、信息素揮發因子a、路徑信息素常量Q、最大迭代次數iter max、迭代次數初值iter=1。

（2）構建解空間

將各個螞蟻放于不同出發點，對每個螞蟻根據概率公式計算其下一個訪問城市，直到遍歷完所有城市。

（3）更新信息素

計算各個螞蟻經過的路徑長度，記錄當前迭代次數中的最優解（最短路徑），同時進行信息素濃度的更新。

（4）判斷是否終止

如果iter< iter max，則令iter= iter+1，清空螞蟻經過路徑的記錄表，返回步驟二;否則，終止計算，輸出最優解。

2.3 DBSCAN密度聚類算法

聚類分析屬于無監督學習，DBSCAN（ Density-Based Spa-tial Clustering of Applications with Noise）是一種典型的基于密度的聚類算法，這類聚類算法一般假定類別可以通過樣本分布的精密程度決定，同一類別的樣本，在該類別任意樣本周圍不遠處一定有同類別樣本存在。將這些緊密相連的樣本劃分為一類，就可以得到一個聚類類別。通過將所有各組緊密相連的樣本劃為各個不同的類別，就可以得到最終的所有聚類類別結果。DBSCAN算法可以將數據點分為三類：1、核心點：在半徑Eps內含有超過MinPts數目的點。2、邊界點：在半徑Eps內點的數量小于MinPts，但是落在核心點的鄰域內的點。3、噪音點：既不是核心點也不是邊界點的點。

03-opt算法的具體流程如下：

Stepl：按圖（2）所示從路徑中刪除3條邊，從別的部分加入三條邊使得路徑保持完整。判斷路徑的交換是否能讓路徑總長度變短，若能，則交換;若不能，則不交換。

Step2：重復執行Stepl，直到遍歷完成所有的可能情況后輸出結果。

相較于其他opt算法，圖（2）中除了交換的各個邊之外，所有的曲線段的方向在交換后都未發生變化，這樣極大地減少了檢查可行路徑的工作量，使得該算法在嵌入到蟻群算法中后整體的算法時間復雜度并未發生明顯變化[15]。

3 改進算法的設計

3.1改進DBSCAN算法鄰域半徑計算

標準DBSCAN算法中，鄰域半徑為常數，且點與點之間的邊權重為點與點之間的距離。而在車輛路徑問題中，每個物料配送點具有各不相同的物料配送需求量，在鄰域半徑的計算中合理考慮每個物料配送點的需求量可以使得聚類劃分的結果更合理。當物料配送需求量較大時，在單次配送中消耗了車輛更多的物料，根據貪心法則，優先考慮將物料配送至物料配送需求量大的物料配送點可以提高單次配送中卡車的物料裝載空間利用率，因此，對于物料配送需求量大的配送點，需要適當增加其鄰域半徑，使其更易被劃分為核心點，具體數學表達式如下：

3.2 改進蟻群算法信息素初始化方案

傳統蟻群算法中，各條路徑上初始信息素濃度相等，這意味著初始信息素分布對算法的收斂不具備導向作用，這也是傳統蟻群算法收斂速度慢，易陷入局部最優的一個重要原因[16]。為了使得初始信息素分布能夠對算法具有合理的導向性，可以通過聚類的劃分區分各個配送點的相對位置[17]，并據此生成聚類，在同一聚類中的各點通過Kruskal算法生成最小生成樹，在所生成的最小生成樹中的各條路徑中初始化信息素，具體表達式如下：

3.3 基于03-opt算法的局部優化方案

在VRP問題的討論中，通常將會存在諸多從配送中心出發完成配送任務后回到起點的子路徑，例如在本文圖（1）所示范例中就存在3條子路徑：1-3-2-4，5-6-7-8，9-10-11-12。為使得算法能有更高的求解精度，在每一次蟻群算法迭代完成后對每一條子路徑進行03-opt局部優化，從而更好地探尋更優解。

3.4 改進算法流程圖

4 實驗內容及結果分析

4.1 算例及初始數據

為驗證算法的有效性，選取一個物流配送的實例情況對問題進行討論。該實例選取（70，40）作為供貨點，各個配送點的相關信息如表1所示，各個基本參數的設置值如表2所示：

其中，p表示信息素揮發參數，N_表示算法運行迭代最大限制次數，表示螞蟻循環一周釋放的信息素總量，m表示螞蟻數，τ0表示不同簇上點之間的信息素初始參數值，τ1表示相同簇上核心點之間的信息素初始參數值，τ2示相同簇上非核心點之間的信息素初始參數值，CAP表示火車最大載重量。

4.2 仿真測試與結果分析

首先通過DBSCAN算法對配送點進行聚類劃分成各個不同的簇，接著對各個簇利用Kruskal生成最小生成樹，結果如圖3所示：

DBSCAN算法的應用成功將各個配送點劃分在不同的簇中，并在簇中生成了最小生成樹。根據本文2.4部分的內容對蟻群算法中的初始信息素矩陣進行更新。之后分別用本文改進后的算法，傳統蟻群算法，傳統粒子群算法和文獻[14]提出的算法通過MATLAB2019A對實例進行1000次仿真測試，并將結果每種算法的1000次仿真測試結果求其均值后觀察每種算法的求解精度與收斂速度。為了更好地衡量算法的收斂速度，這里做如下定義：

當算法得到最佳求解結果時說需要的最少迭代次數值為算法的最佳迭代點。

程序運行結果如表3所示：

1）本文算法;

2）傳統蟻群算法;

3）傳統粒子群算法;

4）文獻[8]提出的算法。

由表3可知，本文所提出的算法在求解該實例時所規劃的路徑相較于其他算法更短，并且有著更小的最佳迭代點，由此可以驗證無論在求解精度還是收斂速度上相較于其他算法都有著明顯的優勢。由此可以驗證，本文所提出的算法有著較高的求解精度，在求解VRP問題時為貨車制定的路徑相較于其他算法更短，為貨運公司節省更多的時間和成本;同時本文算法也有著更快的收斂速度，在解決實際問題時能夠以較小的計算量解決問題，使得方法的應用更快捷，占用更少的時間。

5 結束語

本文通過DBSCAN聚類算法對蟻群算法的初始信息素矩陣進行更新，使得初始信息素分布對算法的合理收斂有著良好的導向性從而得到更精確的結果和更快的收斂速度。然而，本文對于同一簇中的配送點間的信息素的初始化值設定為自定義參數，因此該自定義參數值的選取會對結果產生較大的影響，如果該值過大，則算法收斂速度過快，容易陷入局部最優而影響求解精度;如果該值過小，則算法中初始信息素分布對算法的收斂缺乏良好的導向性，使得收斂速度較慢，且求解精度相對不高，相較于傳統蟻群算法沒有明顯的優勢。此外值得一提的是，算法本身的參數值也會影響算法的求解效果，例如在配送點分布相對較為分散時，DBSCAN算法對于簇的分類效果較差，導致求解精度相較于傳統蟻群算法的提高并不明顯;在配送點需求量較大時，同一簇的配送點需要貨車多次運輸，則本文算法易在迭代初期陷入局部最優。總之，相較于其他算法本文算法對VRP問題的求解有著明顯的優勢，但是依舊存在可改進空間，在之后的研究中，如何確定相關基本參數以及如何選擇性地對同一簇內點間的信息素進行更新成為重點和難點。

參考文獻：

[1] Toth P， Vigo D. Vehicle routing Problems，