空間目標(biāo)的雷達定軌坐標(biāo)轉(zhuǎn)換問題
黃曉斌, 張 燕, 肖 銳
(空軍預(yù)警學(xué)院,武漢 430019)
0 引言
空間目標(biāo)軌道確定是空間目標(biāo)監(jiān)視雷達的一項重要任務(wù),主要的數(shù)據(jù)處理步驟(如圖 1 所示)是:①坐標(biāo)轉(zhuǎn)換;②初軌確定;③軌道改進;④編目。在數(shù)據(jù)處理過程中,涉及到大量的天文學(xué)和數(shù)學(xué)知識。雖然國內(nèi)外已有一些開源定軌軟件可供借鑒,如 OrbFit[1]、ORSA[2]、NEOPROP[3]、Novas[4]、ODTBX[5]等,但這些軟件都是針對天體軌道問題而研發(fā)的,且主要是處理光學(xué)觀測數(shù)據(jù),并不適合處理雷達觀測數(shù)據(jù)。為此,本文開發(fā)了 1 套雷達定軌函數(shù)庫(RadarOrbDet),能夠有助于雷達技戰(zhàn)指標(biāo)的快速實現(xiàn)。RadarOrbDet 庫按照上述4 個處理步驟開發(fā),本文主要介紹其坐標(biāo)轉(zhuǎn)換模塊。
本文通過討論雷達定軌中涉及的基本坐標(biāo)系、坐標(biāo)轉(zhuǎn)換的數(shù)學(xué)原理,給出程序設(shè)計思路,最后利用衛(wèi)星工具包(satellite tool kit,STK)軟件驗證開發(fā)模塊的有效性。

圖1 雷達定軌數(shù)據(jù)處理流程
1 坐標(biāo)系簡介
雷達觀測基于地球坐標(biāo)系,空間目標(biāo)軌道是基于天球坐標(biāo)系,這就涉及到地球坐標(biāo)系與天球坐標(biāo)系之間的轉(zhuǎn)換。
協(xié)議天球坐標(biāo)系由國際天文學(xué)聯(lián)合會(The International Astronomical Union, IAU)和國際地球自轉(zhuǎn)和參考系服務(wù)組織(The International Earth Rotation and Reference Systems Service, IERS)發(fā)布,目前采用的是國際天球參考系(international celestial reference frame, ICRS)。依據(jù)坐標(biāo)原點的不同,ICRS 可分為太陽系質(zhì)心天球參考系(barycentric celestial reference system, BCRS)和地球質(zhì)心天球參考系(geocentric celestial reference system, GCRS)。BCRS 用于計算行星的運動軌道及編制星表;GCRS用于計算衛(wèi)星軌道及編制衛(wèi)星星歷。ICRS 由國際天球參考框架(international celestial reference frame,ICRF)來實現(xiàn)。在1997 年IAU 第23 屆大會上,通過并決定自1998-01-01 起,在天文研究、空間探測、大地測量以及地球動力學(xué)等領(lǐng)域中采用ICRS[6]。
協(xié)議地球坐標(biāo)系由國際地球參考系(international terrestrial reference system, ITRS)實現(xiàn)。GCRS 是1 個相當(dāng)好的準(zhǔn)慣性系,衛(wèi)星的軌道計算一般都是在 GCRS 中進行。這就必須涉及到GCRS 與ITRS 間的坐標(biāo)轉(zhuǎn)換問題[7]。
2 坐標(biāo)轉(zhuǎn)換原理
在雷達定軌中,需要將在站心地平坐標(biāo)系下的雷達觀測數(shù)據(jù)轉(zhuǎn)換到GCRS 坐標(biāo)系中。
2.1 站心地平坐標(biāo)系Xh與ITRS 坐標(biāo)系XGO的轉(zhuǎn)換
站心地平坐標(biāo)系Xh與 ITRS 坐標(biāo)系XGO的定義如表1 所示。

表1 站心地平坐標(biāo)系與ITRS 坐標(biāo)系的定義
站心地平坐標(biāo)系與ITRS 坐標(biāo)系之間的轉(zhuǎn)換公式為

2.2 ITRS 與GCRS 坐標(biāo)系的轉(zhuǎn)換
ITRS 與GCRS 的轉(zhuǎn)換早期是基于春分點的。目前,IERS 2010 年建議使用基于無旋轉(zhuǎn)原點(nonrotating origin, NRO)的轉(zhuǎn)換方法[9]。基于 IAU 2006/2000A-CIO 模型的轉(zhuǎn)換流程[9]如圖2 所示。

圖2 “IAU 2006/2000A-CIO based”坐標(biāo)轉(zhuǎn)換流程
轉(zhuǎn)換過程中涉及到2 個中間坐標(biāo)系:地球中間坐標(biāo)系(terrestrial intermediate reference system, TIRS)和天球中間坐標(biāo)系(celestial intermediate reference system, TIRS)它們的定義見表2。

表2 TIRS 坐標(biāo)系與CIRS 坐標(biāo)系的定義
表 2 中:TIP(terrestrial intermediate pole)為地球瞬時自轉(zhuǎn)軸;TIO(terrestrial intermediate origin)為地球中間零點;CIP(celestial intermediate pole)為天球瞬時自轉(zhuǎn)軸;CIO(celestial intermediate origin)為天球中間零點。
在t時刻,ITRS 和 GCRS 的轉(zhuǎn)換是 2 個 3 維直角坐標(biāo)系間的轉(zhuǎn)換,可以寫成
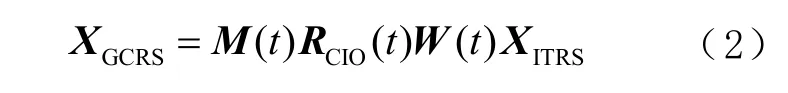
式中:M(t)、RCIO(t)和W(t)分別是由于 CIP 在 GCRS中的運動(歲差章動)、地球的自轉(zhuǎn)以及 CIP 在ITRS 中的運動(極移)引起的旋轉(zhuǎn)矩陣。它們的具體表達式見文獻[9]。
3 程序設(shè)計
圖3 給出了坐標(biāo)轉(zhuǎn)換的程序設(shè)計流程圖,其轉(zhuǎn)換過程分為 3 個部分:①將目標(biāo)在測站地平坐標(biāo)系的極坐標(biāo)轉(zhuǎn)換為ITRS 坐標(biāo)系下的直角坐標(biāo);②根據(jù)轉(zhuǎn)換時刻以及地球定向參數(shù)(Earth orientation parameters,EOP)數(shù)據(jù)形成 ITRS 到 GCRS 的轉(zhuǎn)換矩陣;③將轉(zhuǎn)換矩陣與ITRS 下的直角坐標(biāo)相乘得到GCRS 下的直角坐標(biāo)。轉(zhuǎn)換流程中涉及一些時間系統(tǒng)的轉(zhuǎn)換可參見文獻[7]。圖3 中的“TT 時間”表示地球時(Terrestrial Time)。

圖3 坐標(biāo)轉(zhuǎn)換程序設(shè)計流程
在轉(zhuǎn)換過程中有如下幾個問題應(yīng)該注意:
1)按照式(1)的要求,應(yīng)該輸入站點的天文經(jīng)緯度和地理經(jīng)緯度。前者用來進行坐標(biāo)旋轉(zhuǎn),后者用來計算站點的大地直角坐標(biāo)。但通常只給出站點的地理經(jīng)緯度,在進行坐標(biāo)旋轉(zhuǎn)時,用地理經(jīng)緯度替代天文經(jīng)緯度,2 者雖有細(xì)微的差別,但在絕大多數(shù)場合可忽略不計,如果需要極高坐標(biāo)轉(zhuǎn)換精度時應(yīng)加以區(qū)分。
2)轉(zhuǎn)換過程中需要地球定向參數(shù)(Earth orientation parameters, EOP)數(shù)據(jù),它可從網(wǎng)站下載獲得[10],要注意表中數(shù)據(jù)的有效時段和數(shù)據(jù)條目的時間間隔(通常為1 d)。因此,在給定轉(zhuǎn)換時刻時,通常需要依據(jù)該表插值來獲取更為精確的數(shù)據(jù),而當(dāng)轉(zhuǎn)換時刻超出EOP 數(shù)據(jù)表有效時間范圍時,一般可取最接近該轉(zhuǎn)換時刻的數(shù)據(jù)來替代,但當(dāng)超出時間范圍間隔過大時,其誤差應(yīng)加以考慮。
3)當(dāng)需要極高坐標(biāo)轉(zhuǎn)換精度時,在用EOP 數(shù)據(jù)表插值計算極移和世界協(xié)調(diào)時(coordinated universal time,UTC)與 1 類世界時(universal time,UT1)參數(shù)時,需要額外考慮海潮和固體潮的修正[7],但同時會導(dǎo)致轉(zhuǎn)換速度的下降。
4 軟件接口調(diào)用及有效性驗證
4.1 接口調(diào)用示例
RadarOrbDet 庫坐標(biāo)轉(zhuǎn)換功能的使用方法如下:
步驟①:打開VS2015,新建控制臺應(yīng)用程序,并命名為 radarorddet_Test,輸出模式設(shè)為 64 位Debug,具體方法可參考文獻[11]。
步驟②:從百度網(wǎng)盤下載RadarOrbDet 開發(fā)包[12],并拷貝到工程目錄中,如圖4 所示。

圖4 測試工程目錄結(jié)構(gòu)
步驟③:在radarorbdet_Test.cpp 文件中輸入如圖5 所示的代碼。

圖5 函數(shù)接口調(diào)用示例
4.2 接口函數(shù)有效性驗證
在 STK 11.2 版中仿真 1 顆衛(wèi)星,其軌道參數(shù)設(shè)置如圖 6 所示,測站位置參數(shù)設(shè)置如圖 7所示。

圖6 衛(wèi)星軌道參數(shù)設(shè)置

圖7 測站位置參數(shù)設(shè)置
仿真時間段設(shè)在2016-09-15 UTCG(格林尼治協(xié)調(diào)世界時) 04:00:00 至 2016-09-16 UTCG 04:00:00(STK 沒有最新的EOP 數(shù)據(jù),故設(shè)此時間段保證STK 自帶的EOP 數(shù)據(jù)有效)。利用STK 的報表功能輸出測站對衛(wèi)星的觀測時刻、觀測距離、方位和俯仰數(shù)據(jù),同時輸出STK 內(nèi)部計算所得的衛(wèi)星GCRS 坐標(biāo),坐標(biāo)數(shù)據(jù)的采樣時間段為2016-09-15 UTCG04:00:00 至 2016-09-15UTCG 04:02:00,間隔1 s,總共121 點數(shù)據(jù),圖8(a)顯示了距離測量數(shù)據(jù),圖8(b)顯示了方位測量數(shù)據(jù),圖8(c)顯示了俯仰測量數(shù)據(jù)。
利用 RadarOrbDet 軟件包計算 GCRS 坐標(biāo)(XROD,YROD,ZROD),采用式(3)描述的 GCRS 坐標(biāo)相對誤差與STK 的輸出進行比較,圖9 顯示了相對誤差曲線(實線)。從圖9 中可以看出相對誤差在 1×10-7水平,經(jīng)分析表明,誤差的主要原因是STK 報表以文本方式輸出數(shù)據(jù),導(dǎo)致數(shù)據(jù)產(chǎn)生精度截斷誤差,由此可知軟件包算法是有效的。此外,在圖9 中還繪制了俯仰角曲線(虛線),可以看出當(dāng)俯仰角越小時,轉(zhuǎn)換的誤差越大,其原因是俯仰角越小時,截斷誤差對坐標(biāo)轉(zhuǎn)換誤差的影響越大。
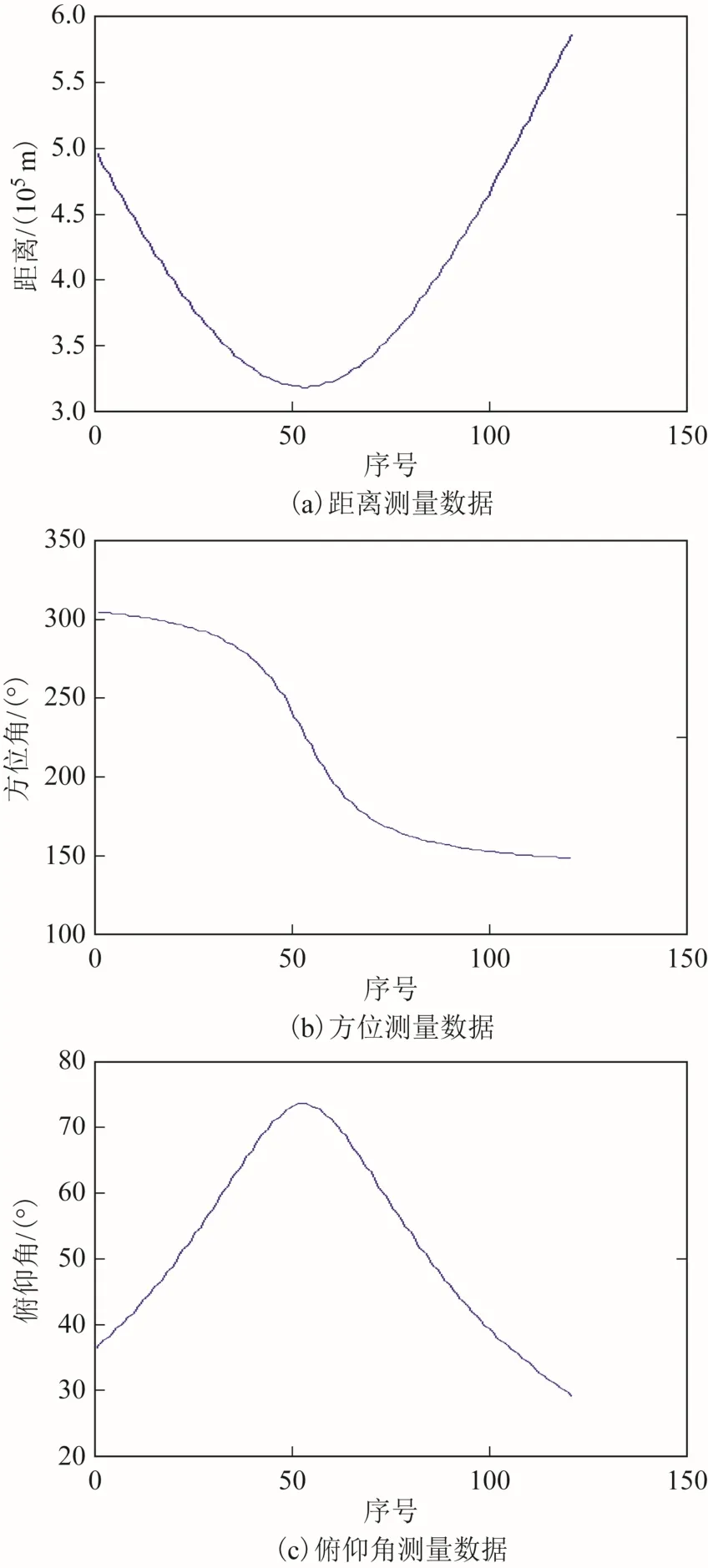
圖8 測站觀測的距離、方位和俯仰數(shù)據(jù)

圖9 GCRS 坐標(biāo)轉(zhuǎn)換相對誤差
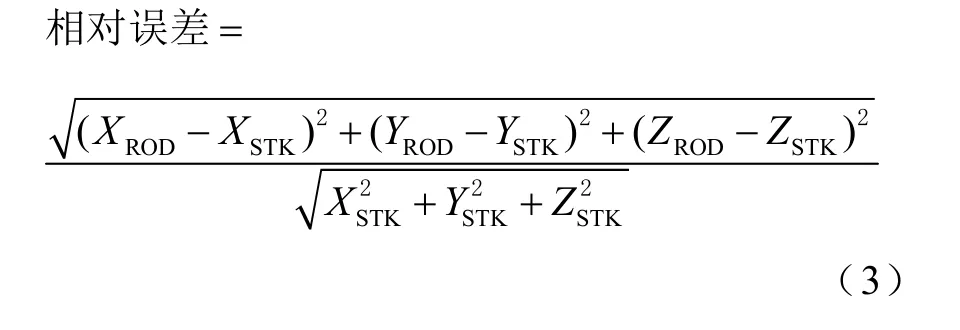
5 結(jié)束語
本文介紹了 RadarOrbDet 庫中坐標(biāo)轉(zhuǎn)換模塊的基本數(shù)學(xué)原理,給出了程序設(shè)計思路,描述了調(diào)用方法,最后用STK 驗證了算法的有效性。下一步將繼續(xù)介紹初軌確定模塊的功能。

