四自由度繩驅動剛柔混合式波浪運動補償機構的動力學建模

姜媛，唐梁，陳原

(山東大學(威海)機電與信息工程學院，山東威海，264209)

船用吊裝設備是實現貨物在船與船之間、船與陸地之間進行交換的媒介。運用于港口碼頭的船用吊裝技術影響貨物的裝卸效率，決定貨物的交換質量與效率，尤其是海軍的后勤遠洋補給，軍艦的裝備補給效率可能影響一場局部戰爭的成敗，因此，發展高技術水平的船用吊裝設備，提高船用吊裝技術，對未來的遠洋補給和作戰具有重大的意義。通常，受波浪的影響，船舶會產生橫移、縱移、升沉、橫搖、縱搖、艏搖6個方向的運動，使得被補給船與補給船之間產生6個方向上的相對運動。船舶之間的相對運動會影響到貨物吊裝的質量，例如，波浪運動造成被補給船和補給船之間發生的升沉相對運動會導致放下的貨物與甲板發生碰撞，或者使貨物再次發生懸空；波浪運動產生船舶之間的橫搖相對運動會造成貨物下放的位置發生偏轉，使其易于與鄰近貨物發生碰撞。為了保證甲板上工作人員和貨物的安全，應減小甚至避免貨物與甲板或者貨物之間碰撞的發生，因此，亟需研制波浪運動補償技術，減少波浪運動對吊裝作業的影響。

現有的波浪運動補償技術大都只對升沉方向的相對運動進行補償，分為被動式和主動式。主動式補償系統通過對母體狀態信號的反饋來控制補償執行器，抗干擾能力強，精度高，補償效果佳，主要有液壓伸縮補償、拖纜絞車收放補償、吊臂變幅式補償等系統類型[1-3]。被動式補償系統多見于升沉方向補償，較為典型的是隨動車補償[4-5]，這種補償系統無需主動控制、提供能源，但補償精度低、性能差。轉運過程中精度與轉運物安全息息相關，隨著世界貿易發展和我國軍事不斷進步，單一升沉或搖擺方向的運動補償已經不能滿足各方需求。為了保證補給的安全性，提高補給效率，國內外對多維方向的波浪運動補償技術進行了研究，它們主要通過繩索驅動的柔性冗余并聯機構或者剛性并聯機構來實現多維方向的波浪運動補償技術。例如，美國海軍研究辦公室研制了六自由度并聯波浪運動補償裝置LVI LO/LO，它使用慣性測量單元和攝像機陣列來檢測艦船之間的相對運動，并通過8根繩索對動平臺實現冗余控制[6]。胡永攀等[7-8]提出了一種繩驅動六自由度并聯式波浪運動補償裝置，研究了該裝置的魯棒控制方法，并進行了抗擺性能分析，但是，這2種六自由度并聯式波浪運動補償裝置都是純繩索驅動冗余并聯機構，而繩索只受拉力不受壓力，當機構動平臺的運動需要繩索伸長時，可能達不到預期的運動參數。邱廣庭等[9-10]提出了一種三自由度剛性并聯式波浪運動補償裝置，該裝置能克服波浪運動對起重機相對運動的影響。LU 等[11]提出了一種3UPU/PU 剛性并聯平臺，用于船舶甲板的自動補償，但是，這2種剛性并聯機構都只具有3個方向上的相對運動補償，在復雜的海況下不能有效地保證貨物轉運的安全。KIM等[12]研制了一種六自由度波浪運動補償裝置，它利用機器視覺來檢測貨物與船舶之間的相對運動，并通過智能平臺來實現波浪運動補償，但是，該機構結構復雜，實用性差。郭霆等[13]提出了一種復合式6-SPS波浪補償穩定平臺，但是，該機構采用雙層結構，所占空間大，控制靈巧性不足。剛性并聯機構能很好地實現動平臺的多維方向運動，可以滿足波浪運動補償過程中對多維方向運動補償的需要，但是，剛性并聯機構受制于驅動和關節運動范圍的限制，其工作空間較小，且機構質量較大，不適宜應用于運動范圍較大的波浪運動補償機構。近年來，繩牽引并聯機構因具有質量小、驅動繩索的長度不受限制、較大的工作空間、自身慣量小等優點而被廣泛關注[14]。然而，繩索只受拉力不受壓力，繩索在伸長過程中可能會得不到預期的速度或加速度，從而影響動平臺的控制效果，甚至引發安全事故。為此，一些國內外學者在繩牽引并聯機構的構型基礎上，引入剛性約束支鏈，構成繩驅動剛柔混合式機構。剛柔混合式結構既具有純繩驅動并聯機構的工作空間大、動態特性好等優點，同時，引入的剛性支鏈增強了該機構的整體剛度，又彌補了繩索只受拉力不受壓力的缺點，使得該機構的控制更加完善。對繩驅動剛柔混合式機構的研究主要有：尚波[15]提出了一種由3根繩索與1個剛性S支鏈組成的兩自由度的新型剛柔結構，將其應用于仿生關節；郭浩[16]提出了一種多連桿繩驅動機器人，該結構的基本單元由4根驅動電纜和1 個被動的S 剛性支鏈組成；KOSSOWSKi等[17]研制了一種柔索驅動桁架，該裝置用6根控制電纜進行驅動，其中用1個由18個旋轉關節組成的被動支鏈來維持結構的穩定性，使結構具有3個平移與1個旋轉四自由度；MAO等[18]研制了一種康復訓練機器人，用7根繩索構建了一個兩層的并聯結構，其中間支鏈由若干關節副串聯組成被動支鏈，實現該機器人模仿人手臂的5個自由度方向的運動；謝少榮等[19]提出了一種混合驅動柔索并聯仿生眼結構，該結構由3根繩索與1個R-S 主動支鏈來實現眼部結構的三維轉動；BEHZADIPOUR 等[20]提出了一種基于電纜牽引的并聯機器人，由3對繩索和1個主動UPU剛性支鏈構成，該結構只具有3個方向上的平移運動。對于剛柔混合式驅動并聯機構，其中間支鏈的結構類型影響其整體結構的自由度，也因此使得剛柔混合式并聯機構廣泛應用于少自由度的需求場合。現有的研究其剛性支鏈大多是一個被動的支鏈，支鏈本身不具有驅動，只起約束作用。在一些實際應用當中，剛性支鏈由若干運動副串聯而成，結構比較復雜。本文作者提出一種新型四自由度剛柔混合式結構，將其應用于波浪運動補償機構。該機構以繩牽引結構為框架，繼承了繩牽引結構的輕盈性、靈活性，保留了大部分工作空間；其剛性支鏈由PS 副串聯連接，支鏈結構簡單，增強了結構的整體剛度，同時，該支鏈還提供直線驅動，彌補了繩索受拉力不受壓力的不足，使得動平臺的運動控制更加完善。

1 繩驅動剛柔混合式波浪運動補償機構的創新設計

補償原理圖如圖1 所示。在貨物的補給過程中，受波浪的影響，船與船之間發生的6個方向上的相對運動會使得補給貨物與被補給船的甲板之間發生碰撞，引發安全事故，特別是升沉方向、橫搖、縱搖和艏搖等4個方向上的相對運動會比其他2 個方向的相對運動帶來更加嚴重的碰撞，因此，本文將創新設計一種補償來自這4 個方向(升沉、艏搖、橫搖、縱搖)的相對運動的四自由度波浪運動補償機構。

在繩牽引并聯機構中，假設其動平臺具有p個自由度，繩索驅動數目為q。為了實現對機構的完全約束定位，繩索張力需要形成封閉矢量，即當繩索驅動數目q=p+1時，繩牽引并聯機構才能夠抵抗作用在動平臺上的外力旋量。對于剛柔混合式并聯機構，要實現機構的完全定位約束，若其剛性支鏈作為被動支鏈，不提供驅動，則其所需要的繩索驅動數目為q=p+1；若其剛性支鏈作為主動支鏈，提供驅動，則其所需要的繩索驅動數目為q=(p-1)+1。故要實現4 個方向的相對運動補償，該波浪運動補償機構需要由4根繩索以及1個剛性的PS 主動支鏈組成。基于此思想，本文設計了如圖2(a)所示的四自由度剛柔混合式波浪運動補償機構。該機構的繩索支鏈由伺服電機帶動絞線盤來控制繩索的伸縮，通過導線盤和動平臺上的鉸點將上平臺和下平臺連接在一起；其剛性支鏈由直線電機控制其移動副的伸縮，該支鏈的上端與上平臺幾何中心固連在一起，下端通過1個球副與下平臺幾何中心連接在一起。通過對繩索以及剛性支鏈運動參數的控制，實現對動平臺位置及姿態的控制。

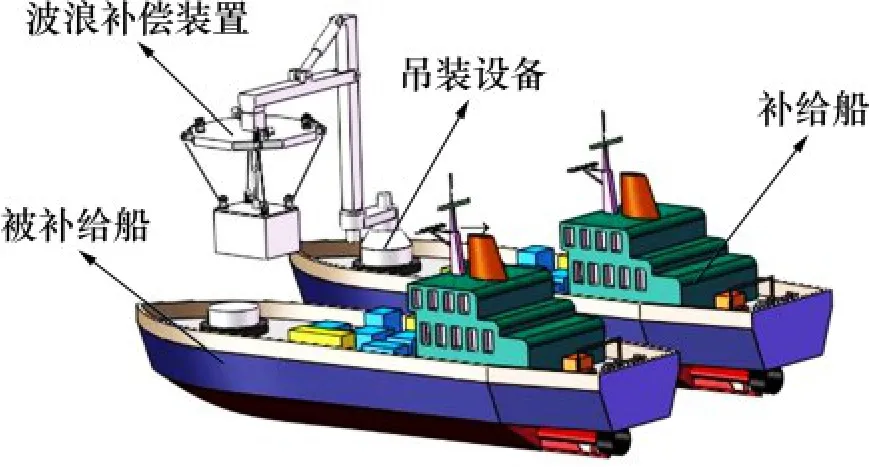
圖1 補償原理圖Fig.1 Compensation principle

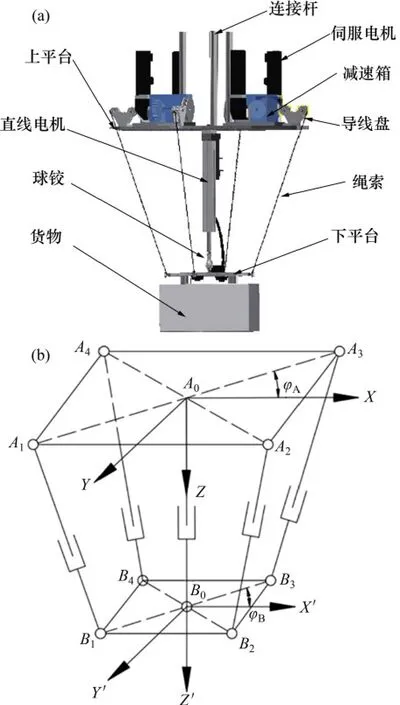
圖2 四自由度繩驅動剛柔混合式波浪運動補償機構Fig.2 Four-degree-of-freedom rope driven rigid-flexible hybrid wave compensation mechanism

將該四自由度繩驅動剛柔混合式波浪運動補償機構安裝在補給船的吊裝設備上。補給船對目標船只進行貨物補給，在貨物吊裝交接的過程中，由波浪產生的相對運動會使貨物不能平穩地放在目標船只的甲板上。此時，可以通過對該波浪運動補償機構中繩索以及剛性支鏈運動參數的控制，使貨物在下放過程中始終與目標船只保持姿態一致，并且在升沉方向上的相對運動速度盡可能小，使貨物釋放后不會再次懸空，也不會對甲板產生較大的沖擊，這樣就有效地保障了貨物補給的安全性。

該四自由度剛柔混合式波浪運動補償機構的結構簡圖如圖2(b)所示，繩索支鏈AiBi(i=1，2，3，4)等效為SPS(S表示球副，P表示移動副)支鏈，剛性支鏈AiBi為PS 支鏈。采用螺旋理論對該機構進行自由度驗證[21]。螺旋的相逆性與坐標系的選擇無關，對支鏈分別建立不同的分支坐標系，對于繩索支鏈AiBi(i=1，2，3，4)，以Ai點球副為原點，建立如圖3所示的支鏈坐標系O-XYZ。

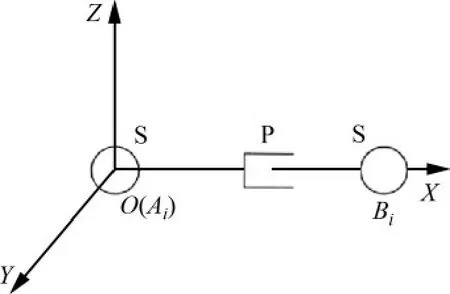
圖3 繩索支鏈AiBi的坐標系Fig.3 Coordinate system of rope branch AiBi

在繩索支鏈AiBi坐標系下的運動螺旋系SAiBi為

式中：li為繩索支鏈AiBi(i=1，2，3，4)的長度。

經計算，該螺旋系的秩rank(SAiBi)=6，不存在反螺旋系，4條繩索支鏈AiBi都屬于六自由度分支。同理，以Ai球副的中心為原點，建立了如圖4所示的PS剛性支鏈A0B0的O-XYZ支鏈坐標系。

PS 剛性支鏈在剛性支鏈坐標下的螺旋系SA0B0為

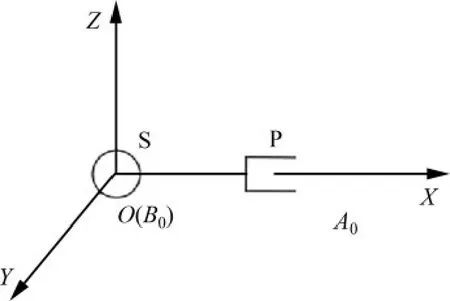
圖4 PS剛性支鏈坐標系Fig.4 Coordinate system of rigid branch PS

求得該螺旋系的反螺旋系為

該支鏈被約束了2個自由度，即沿X軸方向的移動和沿Y軸方向的移動，因此，該波浪運動補償機構具有3個轉動1個移動四自由度(繞X，Y，Z的轉動以及沿Z軸的移動)。對于由1個少自由度的串聯分支和若干個6自由度分支構成的第1類非對稱并聯機構，其自由度完全決定于其少自由度串聯支鏈，因此，該補償機構滿足結構設計要求。

2 繩驅動剛柔混合式波浪運動補償機構的運動學建模

2.1 機構的位置反解

機構位置反解是在已知動平臺在空間的位置和姿態條件下，求解繩子以及剛性移動副的伸縮位移，即已知動平臺的位姿(ZB0，α，β，γ)，求各驅動支鏈的長度L(l0，l1，l2，l3，l4)。

在機構的靜平臺(上平臺A)建立固定坐標系A0-XYZ，以靜平臺的幾何中心A0為原點，X 軸、Y軸、Z軸的方向如圖2(b)所示。在機構的動平臺(下平臺B)建立動坐標系B0-X′Y′Z′，以動平臺的幾何中心B0為原點，X′軸、Y′軸、Z′軸的初始方向分別平行于固定坐標系的X軸、Y軸、Z軸。

在靜平臺A 中，各鉸點在固定坐標系A0-XYZ中的坐標為Ai(AixAiyAiz)，各鉸點相對于固定坐標系原點A0的矢徑用rAi表示。動平臺各鉸點Bi在動坐標系B0-X′ Y′ Z′中的坐標表示為B′i(B′ixB′iyB′iz)，各鉸點相對于動坐標系原點B0的矢徑用rB'i表示，各鉸點相對于固定坐標系原點A0的矢徑用rBi表示。用X-Y-Z 型歐拉角描述動平臺相對于靜平臺的運動，則動平臺相對于靜平臺的位姿就可以用3個角度α，β和γ描述，動坐標系相對于固定坐標系的姿態變換矩陣為

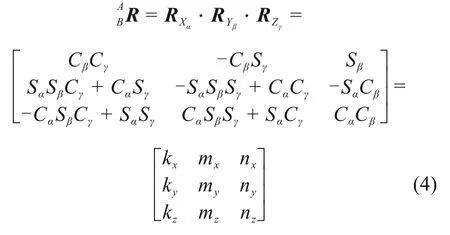
通過坐標變換轉換到固定坐標系中，相對于原點B0的矢徑rB'i動平臺中的任一鉸點在固定坐標系中的矢徑rBi為

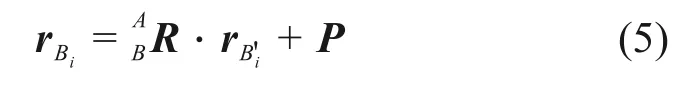
則驅動繩以及剛性支鏈的位移矢量Li(i =0,1,…,4)在固定坐標系中表示為

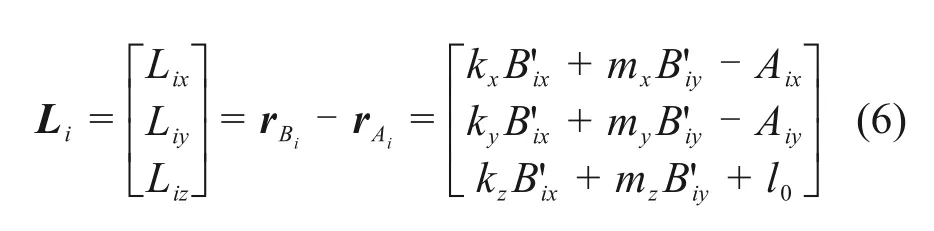
各支鏈長度li的方程可以表示為

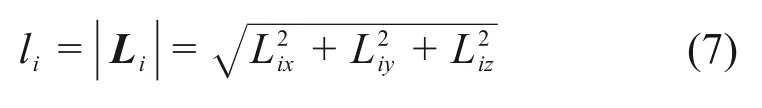
式(7)即為繩驅動剛柔混合式波浪運動補償機構的位置反解。根據具體的機構尺寸以及動平臺的位置和姿態(ZB0，α，β，γ)，可求出各個驅動的位移L(l0，l1，l2，l3，l4)。表1 所示為動平臺的3 組反解算例。

2.2 機構的位置正解

求機構的位置正解，即在已知繩子以及剛性移動副的伸縮位移條件下，求動平臺在空間的位置和姿態，即已知各驅動的長度L(l0，l1，l2，l3，l4)，求動平臺的位姿(ZB0，α，β，γ)。

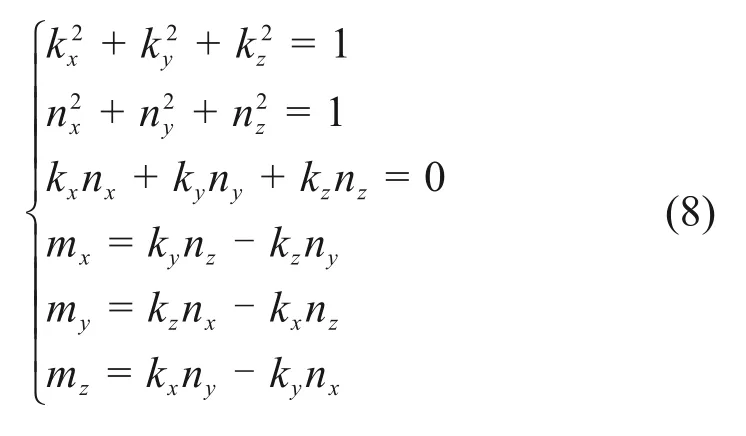
同時，由方程的位置反解可以得到

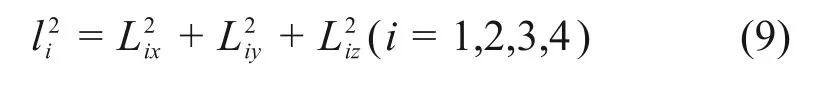
聯立方程組(8)以及式(9)，運用數值迭代法可以求得旋轉矩陣中9個元素的解。然后，由旋轉變換矩陣(4)可以得到α，β，γ的表達式：

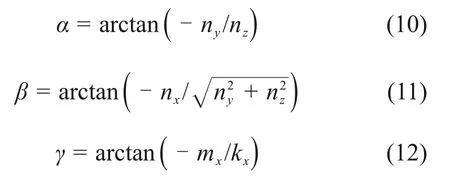
又由機構的結構可知：

當已知各驅動的長度L(l0，l1，l2，l3，l4)時，可求得該動平臺的位姿(ZB0，α，β，γ)，即求得該動平臺位置正解。將表1 中得到的位移作為輸入，得到如表2所示的動平臺的輸出位姿，將輸出位姿與給定位姿進行對比得到位姿誤差。由表2 可知：位姿誤差較小，皆在10-5的數量級內，說明了本文所提出的位置正解與位置反解模型的正確性。

2.3 機構的速度分析

對位置反解式(7)兩端分別對時間求導，可得第i根驅動繩的速度l˙i：

式中：ei=Li/li，為沿Li方向的單位向量；vBi為動平臺各鉸點Bi的速度，

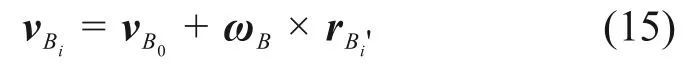
vB0=[vx，vy，vz]T，為動平臺中心點B0的線速度；ωB=[ωx，ωy，ωz]T，為動平臺的角速度。

將式(15)代入式(14)得

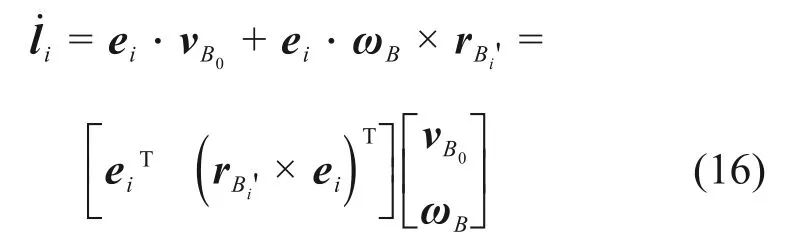
對于全部5根驅動繩，有：

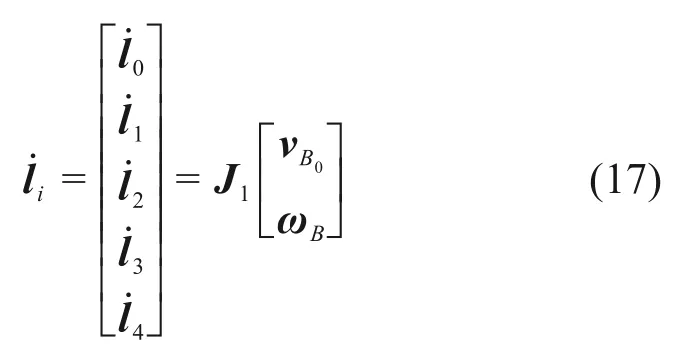
表1 動平臺的位置反解算例Table 1 Counter-solution example of moving platform

表2 動平臺的位置正解算例Table 2 Positive position solution example of moving platform

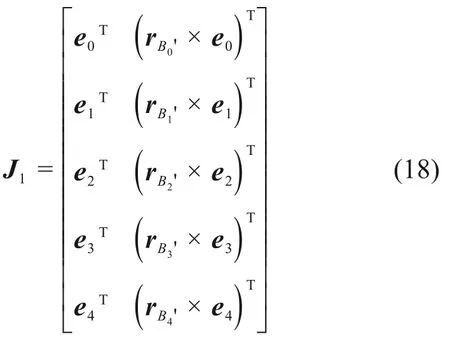
式中：J1為驅動速度與動平臺六維速度間的映射矩陣。

用X-Y-Z歐拉角(α，β，γ)表示動平臺的姿態，將歐拉角對時間的導數α˙，β˙和γ˙轉換到定坐標系中，則動平臺的角速度用歐拉角的導數可以表示為

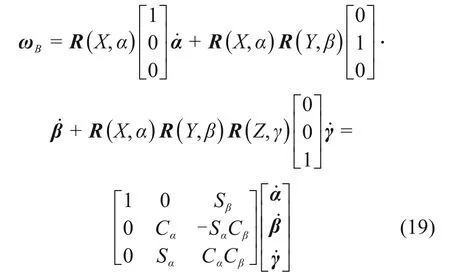
式中：R( X,α )，R( Y,β )和R( Z,γ )分別為繞X，Y，

Z軸旋轉α，β和γ角的旋轉矩陣。動平臺的速度可用線速度和角速度表示為

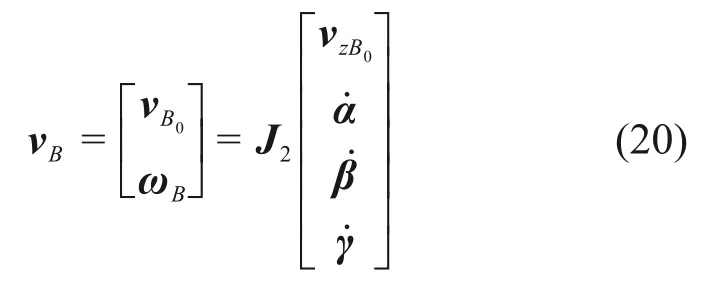
其中：

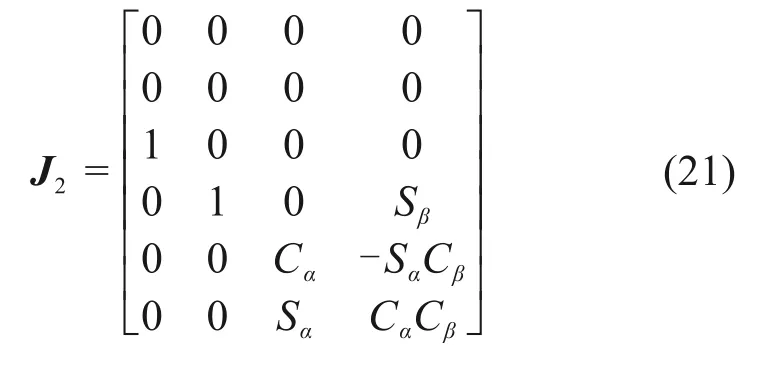
將式(20)代入到式(17)得：

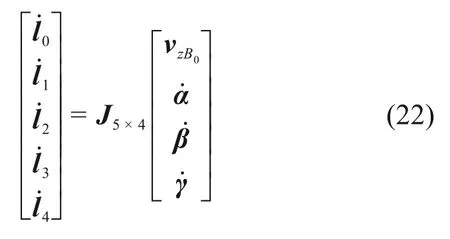
式中：J5×4=J1*J2∈R5×4表示該機構的雅克比矩陣。

2.4 機構的加速度分析

設ɑ=[ɑxɑyɑz]T和ε=[εxεyεz]T分別表示動平臺的線加速度和角加速度，ɑli表示沿Li(i=0，1，…，4)方向上的加速度。對式(16)兩端對時間分別求導得

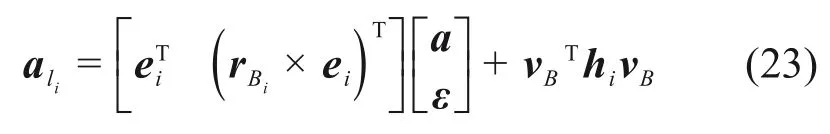
將式(20)兩端分別對時間t求導得

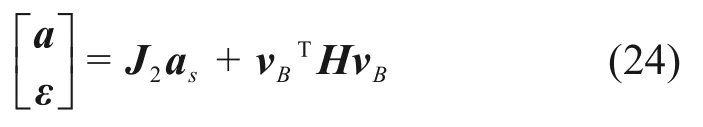
3 繩驅動剛柔混合式波浪運動補償機構的動力學建模

3.1 動平臺的動力學模型

動平臺的受力如圖5 所示。圖5 中，m 為動平臺的質量；Fe為加載在動平臺上的外力；Me為加載在動平臺上的外力矩，I為運動平臺在中心點的慣性張量，vB0和ωB分別為動平臺中心點的速度和角速度。

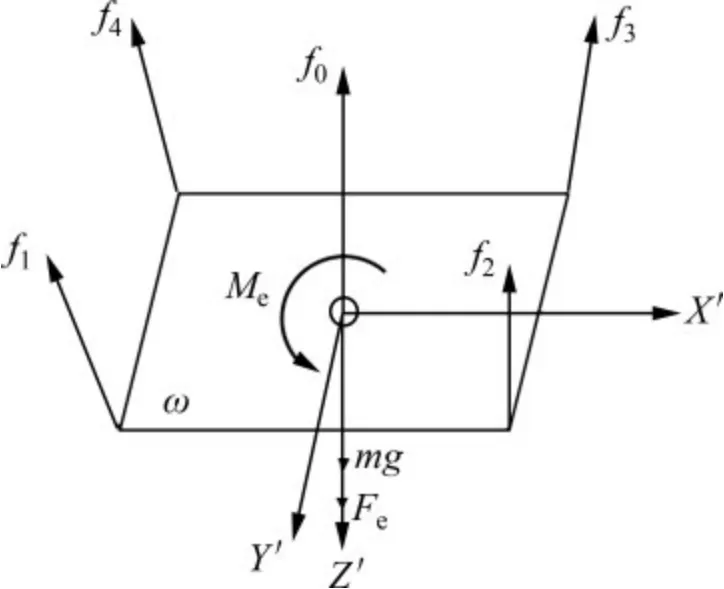
圖5 動平臺的受力模型Fig.5 Force model of moving platform

動平臺的動力學模型由平臺的移動和轉動這2部分組成，因此，動平臺的動力學模型可以表達成如下式子：

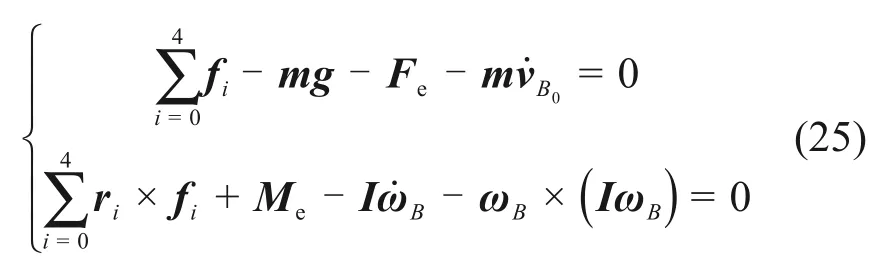
將式(25)改寫成矩陣形式：

式中：D =

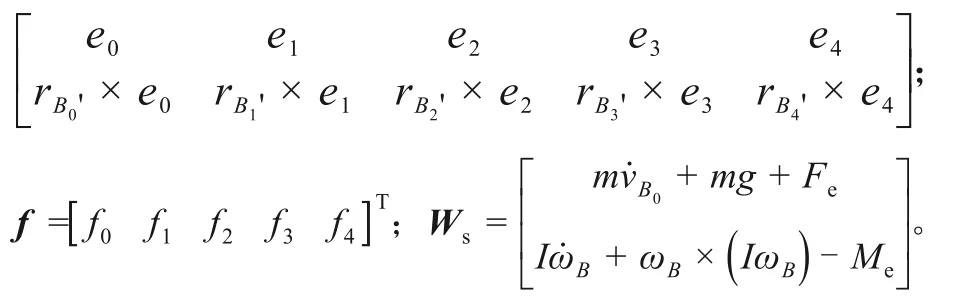
3.2 繩索驅動器的動力學模型

繩索驅動器的受力模型如圖6 所示。圖6 中，Jr為驅動單元的等效轉動慣量；φi為第i 個電機的轉角矢量，以繩索長度的增加方向為正方向，當動平臺在初始位置時，設定φi=0；Cr為繩索驅動單元的等效阻尼系數矩陣；R為繩索驅動器的等效半徑；fi為第i 根繩索的拉力；Ma為驅動器的轉矩。由牛頓第二定律可以建立如下動力學模型：

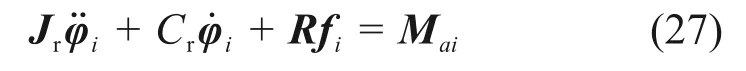
可以將式(27)改寫為如下矩陣形式：

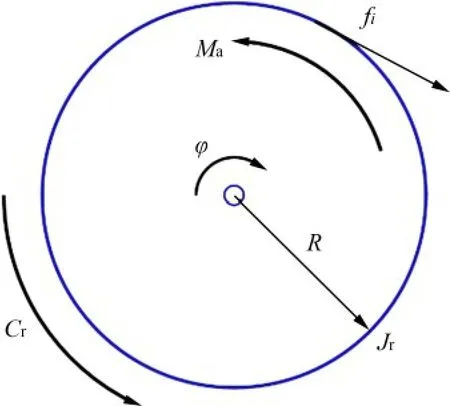
圖6 繩索驅動器的受力模型Fig.6 Force model of rope drive

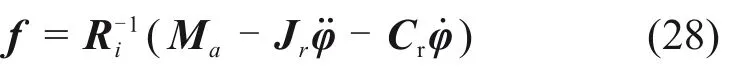
式中：f=[f1f2f3f4]T；Ri=diag[R1R2R3R4]；Ma=[Ma1Ma2Ma3Ma4]T；Jr=diag[Jr1Jr2Jr3Jr4]；φ=[φ1φ2φ3φ4]T；Cr=diag[Cr1Cr2Cr3Cr4]。

3.3 驅動剛柔混合式波浪運動補償機構的動力學模型

聯立動平臺的動力學模型與驅動器的動力學模型，可以建立驅動剛柔混合式波浪運動補償機構的動力學模型。由幾何關系可得第i根繩索的變化量Δli與第i個電機的轉角矢量φi存在以下關系：

對式(29)兩邊同時對時間求導，可以求得如下轉角矢量φ的速度和加速度：

將式(30)代入繩驅動器動力學方程(28)，可以得出繩驅動器動力學方程：

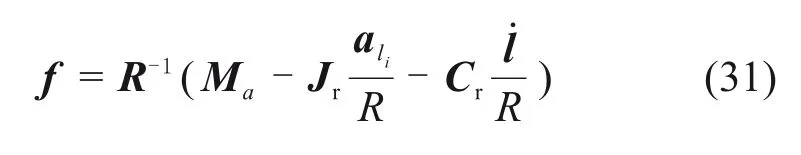
聯立驅動器的動力學方程(31)和動平臺的動力學方程(26)，可以求得驅動剛柔混合式波浪運動補償機構的動力學方程：

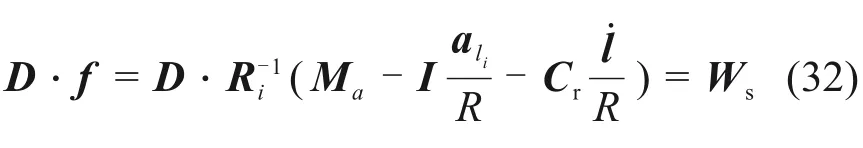
4 數值仿真算例

定義波浪運動補償裝置的結構參數如下：靜平臺的長為320.00 mm，寬為554.26 mm；動平臺的長為316.5 mm，寬為125.0 mm；動平臺初始位置為水平，其中心點的初始位置為[0,0,-367.14]；繩索驅動器的等效半徑R=50 mm。不考慮繩索的質量以及繩索與滑輪之間的摩擦力。

4.1 運動學模型的數值仿真

建立該波浪運動補償裝置的Adams 模型，對該模型進行運動學仿真，得到如圖8所示各驅動的運動學參數。圖8(a)中，各驅動的長度變化平滑，與圖7(a)中的驅動長度變化相一致。圖8(b)中，各驅動的速度變化較為平滑，在大部分時間內與圖7(b)所示變化趨勢保持一致，在1.5 s 左右處出現跳動， 最大誤差為5.327 mm/s， 平均誤差為2.141 mm/s，為理論計算值的1.4%，在可接受誤差范圍內。圖8(c)中，各驅動的加速度變化在大部分時間與圖7(c)所示變化趨勢保持一致，在0.5 s 和1.5 s處出現小幅波動，波動的誤差為±1.237 mm/s2，在可接受的范圍內。

圖7 運動學模型的數值仿真Fig.7 Numerical simulation of kinematics model

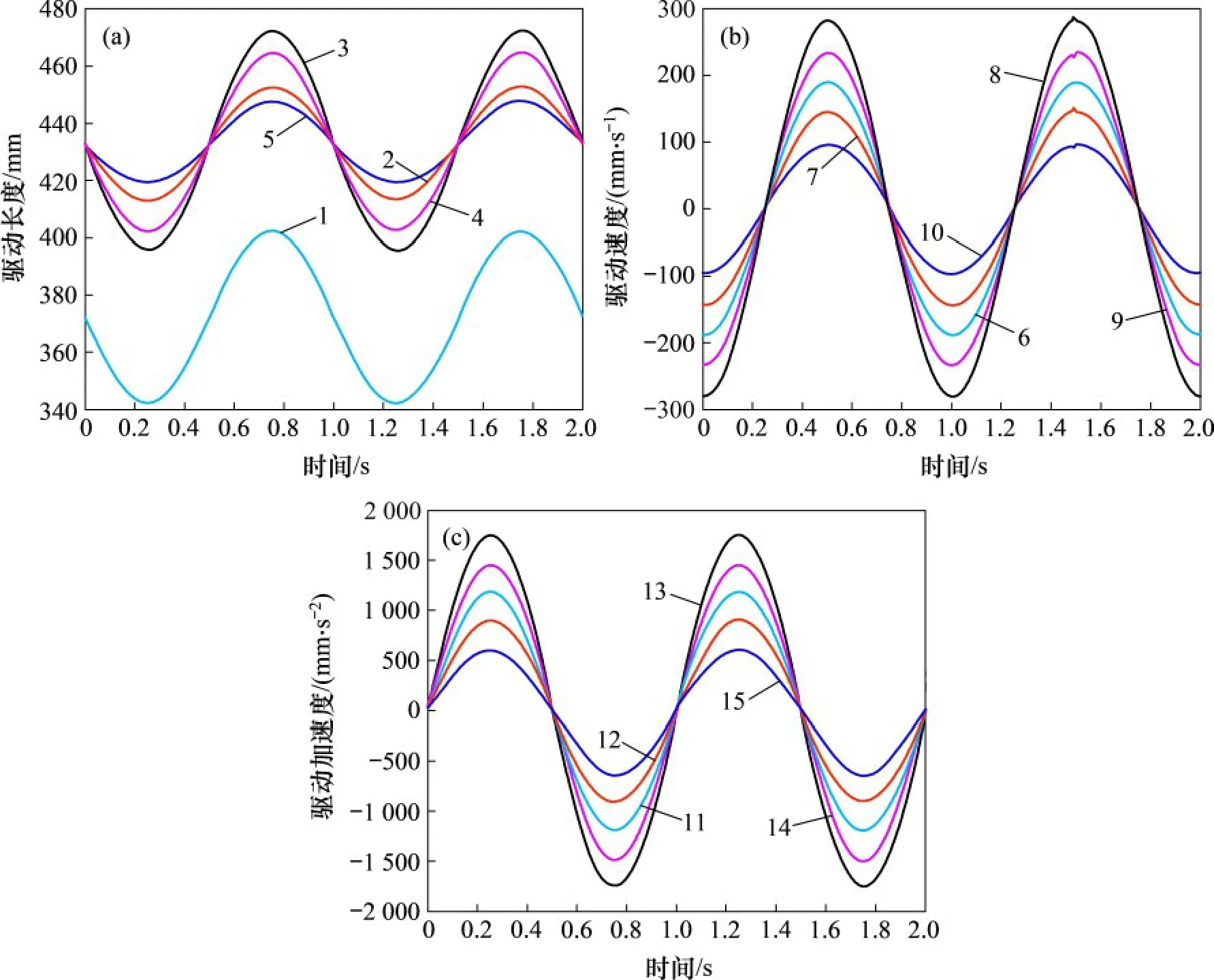
圖8 虛擬樣機的Adams運動學仿真Fig.8 Adams kinematics simulation of virtual prototype

通過將Adams 運動學仿真所得到的驅動運動學參數的結果與MATLAB 數值模擬所得到的結果進行對比發現：在所給周期內，其驅動的長度、速度以及加速度基本一致，誤差在可接受范圍以內，證明了本文所推導的位置反解、速度模型以及加速度模型是正確的。

4.2 動力學模型的數值仿真

根據所推導的動力學公式得到MATLAB 數值模擬結果，如圖9 所示，將其與如圖10 所示的Adams動力學仿真結果進行比較。

將虛擬樣機的Adams 動力學仿真與動力學模型的數值仿真圖進行分析發現：剛性支鏈與繩索的受力連續，不存在受力突變的位置，且繩索受力一直為正，處于張緊狀態，說明了該結構具有良好的受力特性。將虛擬樣機的Adams 動力學仿真與動力學模型的數值仿真圖進行對比分析，發現無論是剛性支鏈還是繩索支鏈，其受力的大小以及變化趨勢基本保持一致。進一步地，以剛性支鏈為例進行誤差分析，得到如圖11 所示的剛性支鏈受力對比圖。由圖11 可知：MATLAB 和Adams 拉力仿真結果及其變化趨勢基本吻合，誤差的最大值出現在1.37 s 左右，最大誤差為0.43 N，為理論計算值的1.6%，在可接受的范圍內。

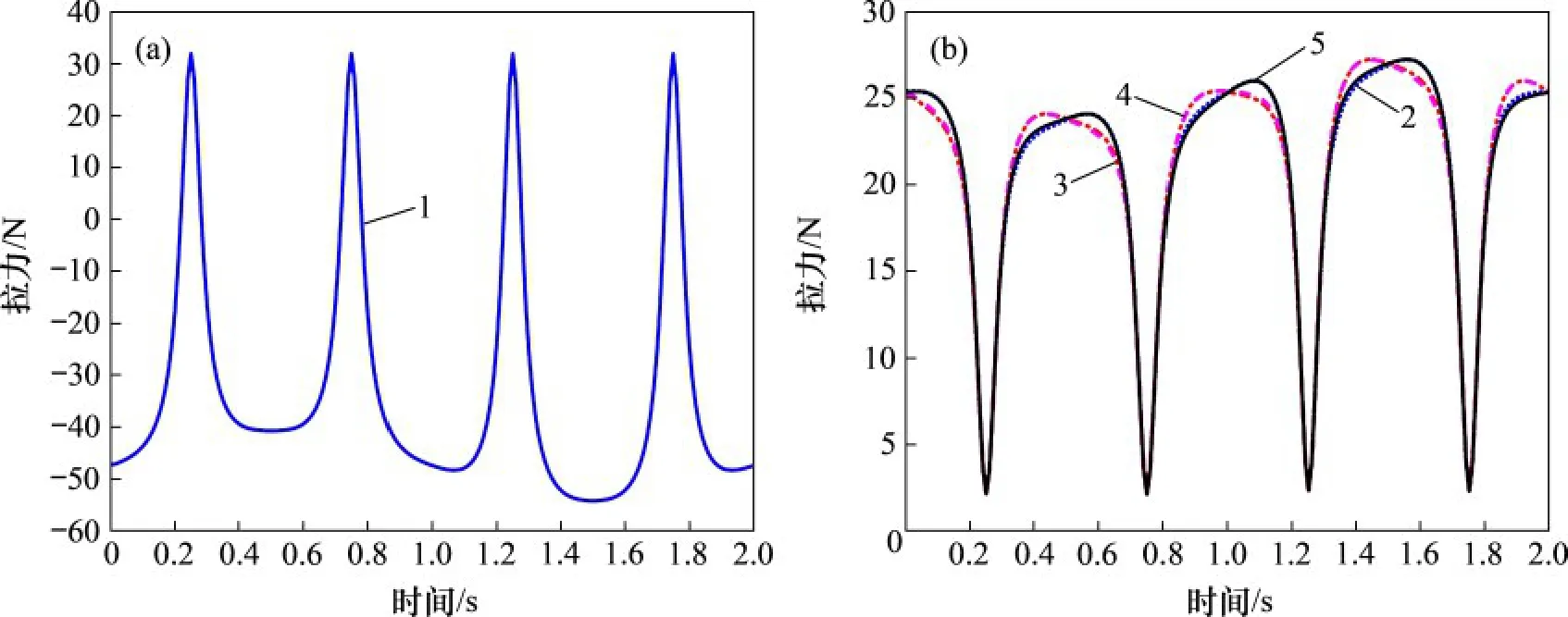
圖9 動力學模型的數值仿真Fig.9 Numerical simulation of dynamic model

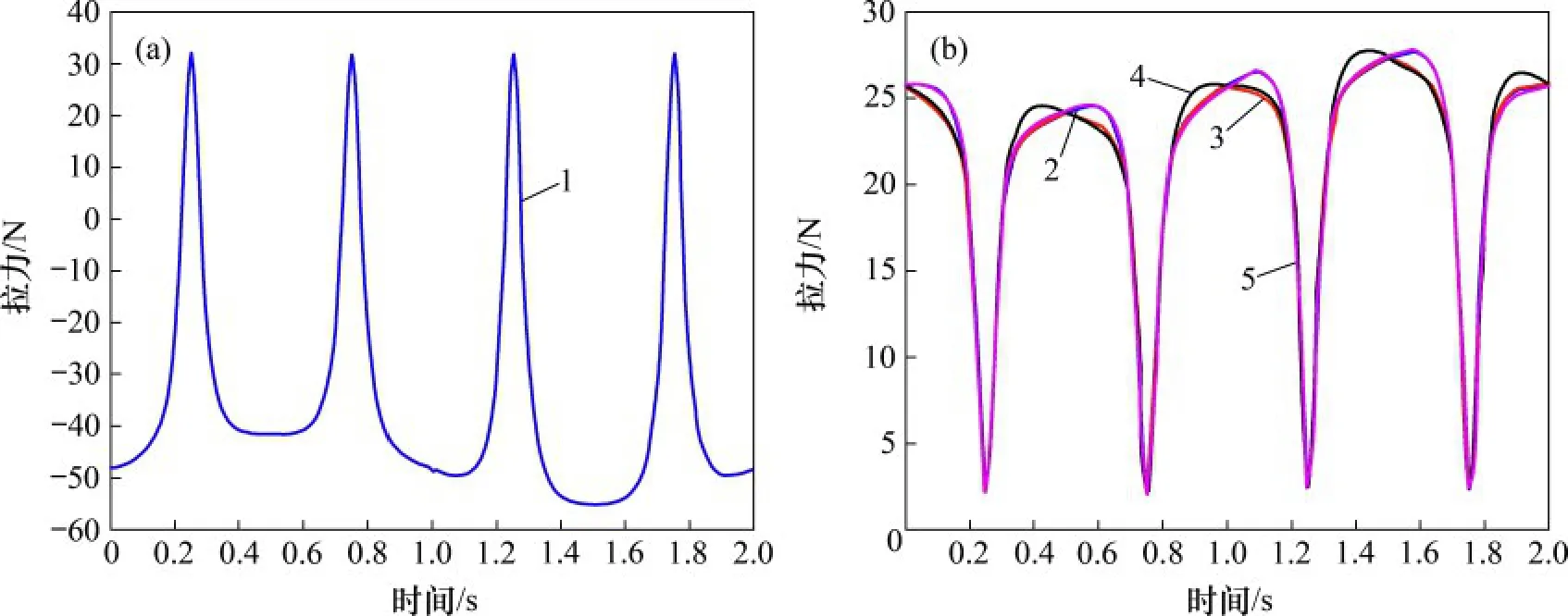
圖10 虛擬樣機的Adams動力學仿真Fig.10 Adams dynamics simulation of virtual prototype

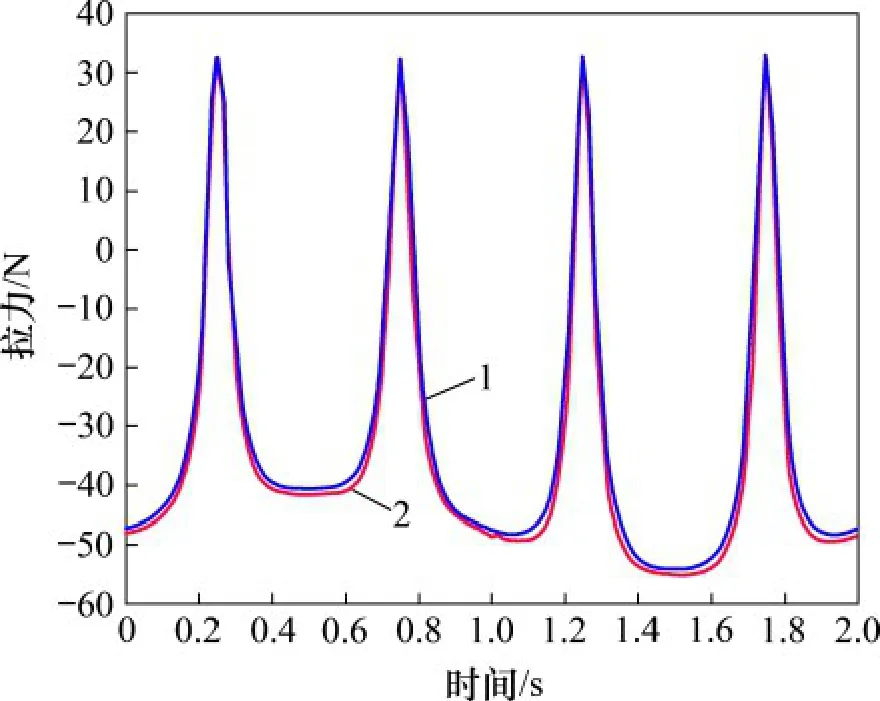
圖11 剛性支鏈受力對比圖Fig.11 Comparison chart of rigid branch force

通過對比發現，繩索拉力的仿真曲線和理論計算曲線在所給周期內基本保持一致，誤差在可接受范圍內，可以忽略不計，驗證了所推導的動力學的正確性。

5 試驗

為驗證模型動平臺的姿態的動態特性，結合實際參情況優化參數，搭建了實驗樣機，如圖12所示。

圖12 實驗樣機Fig.12 experimental prototype

將船舶3個方向的搖擺運動用3組幅值與周期不同的旋轉正弦函數表示，如表3所示。

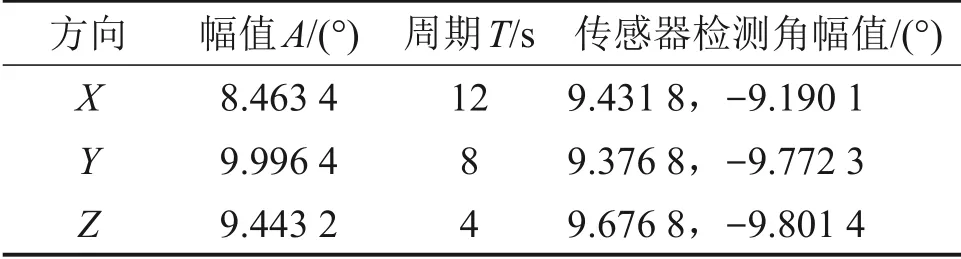
表3 旋轉正弦函數Table 3 Rotate sine function

分別比較各軸傳感器檢測角幅值與目標正弦函數幅值，得到絕對值誤差均為1°左右。對3組測量的旋轉角數據與輸入函數圖像進行擬合，結果如圖13所示。

從圖13可以看出：X方向和Z方向幅值稍大于傳感器檢測幅值，而Y方向幅值稍小于傳感器檢測幅值，誤差主要是由繩索的彈性變形和步進電機的控制精度不足引起。動平臺偏轉結構示意圖如圖14 所示。此機構中，繩索A 和B 的拉力相等，橫截面變化可忽略不計，因此，變形的主要影響因素為繩長。橫搖與艏搖過程中繩索A 的伸長量比繩索B的大，導致偏角增大；而縱搖時，支鏈A和B長度變化小，張緊力大，電機驅動受到的阻尼較大，導致繩索支鏈長度變短，導致偏角減小。陀螺儀受環境影響，也可能導致誤差出現。

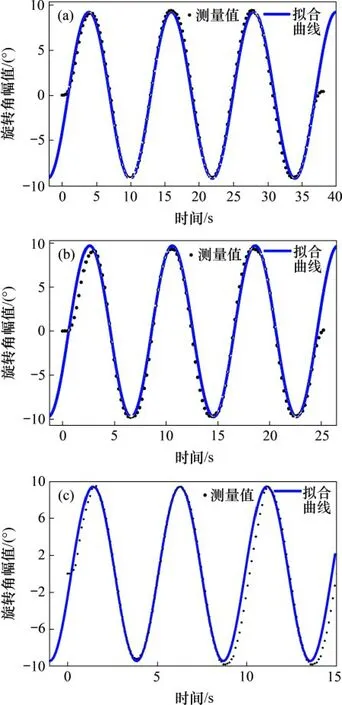
圖13 搖擺幅度擬合曲線Fig.13 Fitting curves of swing amplitude

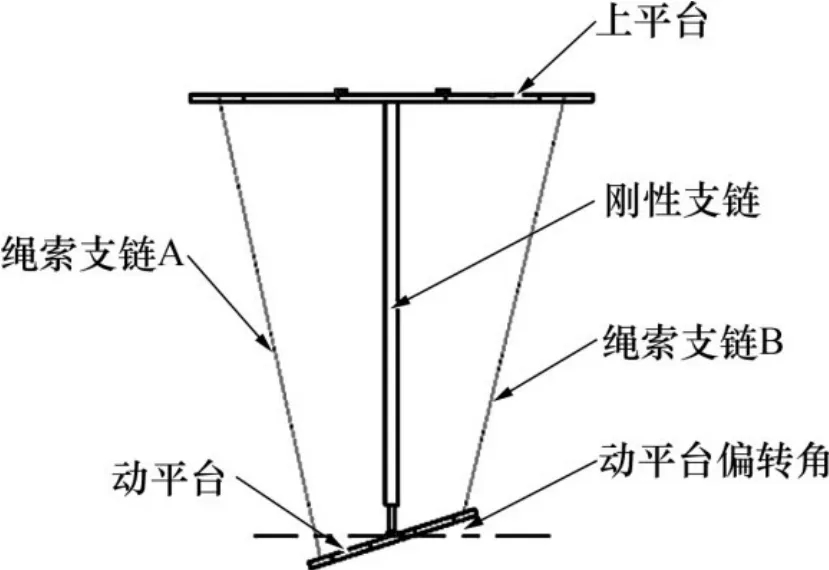
圖14 動平臺偏轉結構示意圖Fig.14 Schematic diagram of deflection structure of moving platform

6 結論

1)提出了一種用于四自由度繩驅動剛柔混合式波浪運動補償機構，基于螺旋理論驗證了其運動自由度，能滿足波浪運動補償的運動需求。

2)建立了該波浪運動補償裝置的位置正解與位置反解。利用數值迭代法對位置正/反解進行計算，位置誤差都在10-5mm數量級，驗證了位置正/反解模型的正確性。

3)推導了該波浪運動補償裝置的運動學模型，基于牛頓-歐拉法推導了該裝置的動力學模型。運用仿真軟件對所推導的數學模型進行驗證，發現MATLAB 數值模擬結果與Adams 虛擬樣機所得結果基本吻合，誤差最大值為理論值的1.6%，在可接受范圍內，驗證了所推導的運動學與動力學模型的正確性。

4)通過實驗檢測了橫搖、縱搖和艏搖的動態特性，輸入幅值與測量幅值的誤差較小，驗證了機構運動學模型的正確性。