利用混沌吸引子階躍變化現象檢測滾動軸承微弱故障

閆曉麗，唐貴基，王曉龍

(華北電力大學能源動力與機械工程學院，河北保定，071003)

在機械設備故障發生的早期，故障信號相對于噪聲較為微弱。傳統去噪方法在消除信號噪聲的同時，有可能將表征故障特征的信號一同濾除，繼而得出錯誤的檢測結論，因此，傳統故障檢測方法對被檢信號的信噪比要求較高，在早期微弱故障檢測的應用中受到了限制[1]。自20 世紀90年代以來，BIRX 等[2]將混沌振子用于微弱信號檢測后，國內外學者針對基于混沌振子的微弱信號檢測做了大量的工作[3-9]。混沌是服從確定性規律但具有隨機性的運動，其隨機性表現為初始條件和參數的微小差異有可能導致結果的顯著不同，同時，混沌系統對噪聲有較強的免疫性[10]。基于混沌振子的微弱信號檢測正是利用混沌系統的參數敏感性和抗噪性，對淹沒在背景噪聲信號中的微弱信號進行檢測。此類方法不是通過消除或抑制噪聲來提取微弱信號的特征，而是利用非線性系統本身特性，在強噪聲背景下檢測微弱信號成分[5]。目前，應用于微弱故障診斷的混沌振子類型有Duffing 振子[6]、Lorenz 振子[7]以及一些耦合混沌振子[8]。這些檢測系統大多是利用參數改變使混沌狀態發生變化的原理進行設計的。基于混沌振子的微弱信號檢測方法關鍵在于混沌狀態判斷和閾值選取[9-13]，目前，人們主要研究混沌狀態與周期狀態轉變的判斷方法[14-17]，關于混沌狀態之間或周期狀態之間的轉變過程的研究較少，而且現有混沌狀態判據仍存在定性混沌判據計算過程復雜，運算時間長，定量混沌判據的混沌狀態的臨界點難以確定，閾值選取不夠精確的問題[18-20]，難以在工程實際中應用。因此，研究簡單有效的混沌振子狀態變化判據和閾值選取方法，對提高基于混沌振子的微弱故障信號檢測方法性能具有重要意義。本文作者首先分析典型的混沌系統的吸引子形狀的階躍變化特性；然后在吸引子形狀階躍變化的基礎上，提出自適應選取閾值方法和自動判據混沌吸引子階躍變化的方法，并設計基于混沌系統吸引子階躍變化的微弱信號檢測系統；最后通過對仿真信號和實測滾動軸承的微弱故障信號的檢測實驗，驗證了方法的有效性。

1 混沌振子吸引子階躍變化現象

在整數階混沌系統中，一些特定參數為臨界值時，混沌吸引子與其吸引盆邊界接近重合，吸引子的相圖會發生明顯變化，轉變為另一種穩定的周期狀態或另一形式的混沌[12]，因此，混沌系統吸引子形狀的變化不僅發生在混沌狀態與周期狀態的轉化過程中，而且系統由周期狀態向另一周期狀態或從一種混沌狀態向另一種混沌狀態轉變同樣可能引起系統吸引子形狀變化。吸引子的變化是由系統狀態變化引起的，能夠反映參數的變化。本文通過研究Duffing 和Lorenz 這2 類典型的混沌振子的吸引子階躍變化現象驗證這一結論。

1.1 Duffing振子的吸引子階躍變化現象

Duffing 振子是目前應用最為廣泛的混沌振子微弱信號檢測系統，其動力學狀態方程為

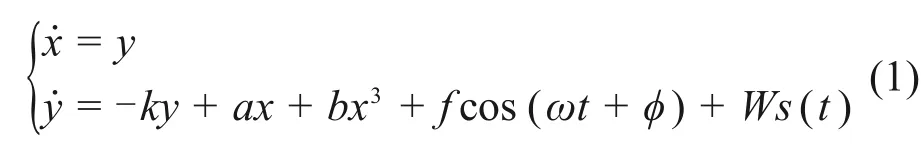
式中：k為阻尼系數；ax + bx3為恢復力項，x為狀態變量，a 和b 為系數；f cos(ωt + φ)為強迫項，f為強迫項幅值，ω為強迫項角頻率，φ為強迫項初始相位；W為輸入信號的加權因子；s(t)為輸入信號。參考關于Duffing振子的文獻[8-11,14-16]，設定系統的參數為k = 0.5，a = -1，b=1，ω=1 rad/s，φ= 0。系統處于無輸入信號的狀態。求解得到狀態變量x隨f變化的Duffing系統局部分岔圖，結果如圖1所示。

由圖1 可知：Duffing 振子是由倍周期分岔通向混沌的。在參數f變化的過程中，Duffing系統在0～f1之間為同宿軌道，在f1～f2范圍內經歷了倍周期分岔的變化，過渡到f2～f3范圍內的混沌狀態，隨后周期、混沌等多種狀態交替出現。在分岔圖中，可以觀察到狀態變量x 在f2前后發生了明顯階躍性變化。

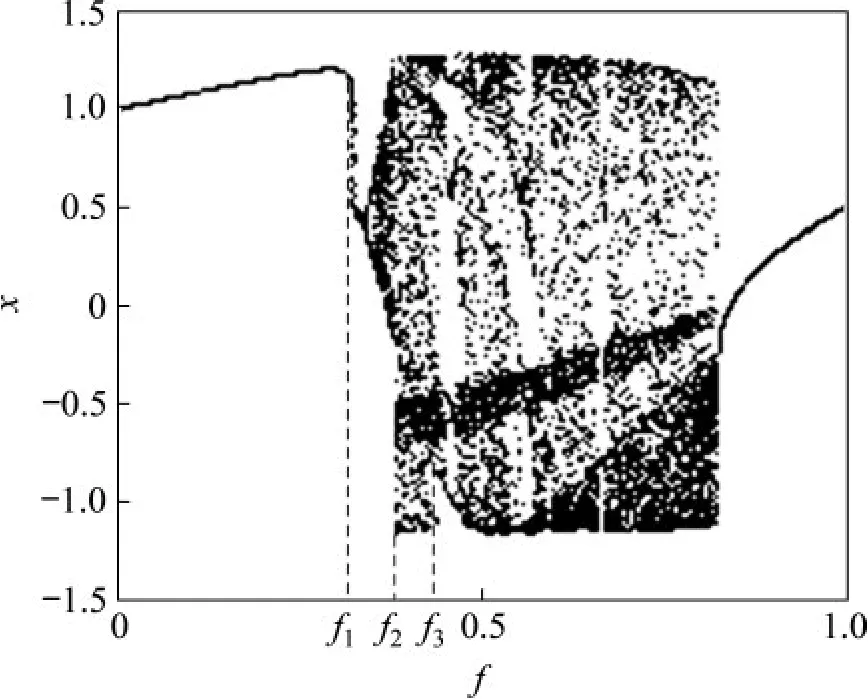
圖1 Duffing振子分岔圖f ∈[0,1]Fig.1 Bifurcation diagram of Duffing oscillator f ∈[0,1]

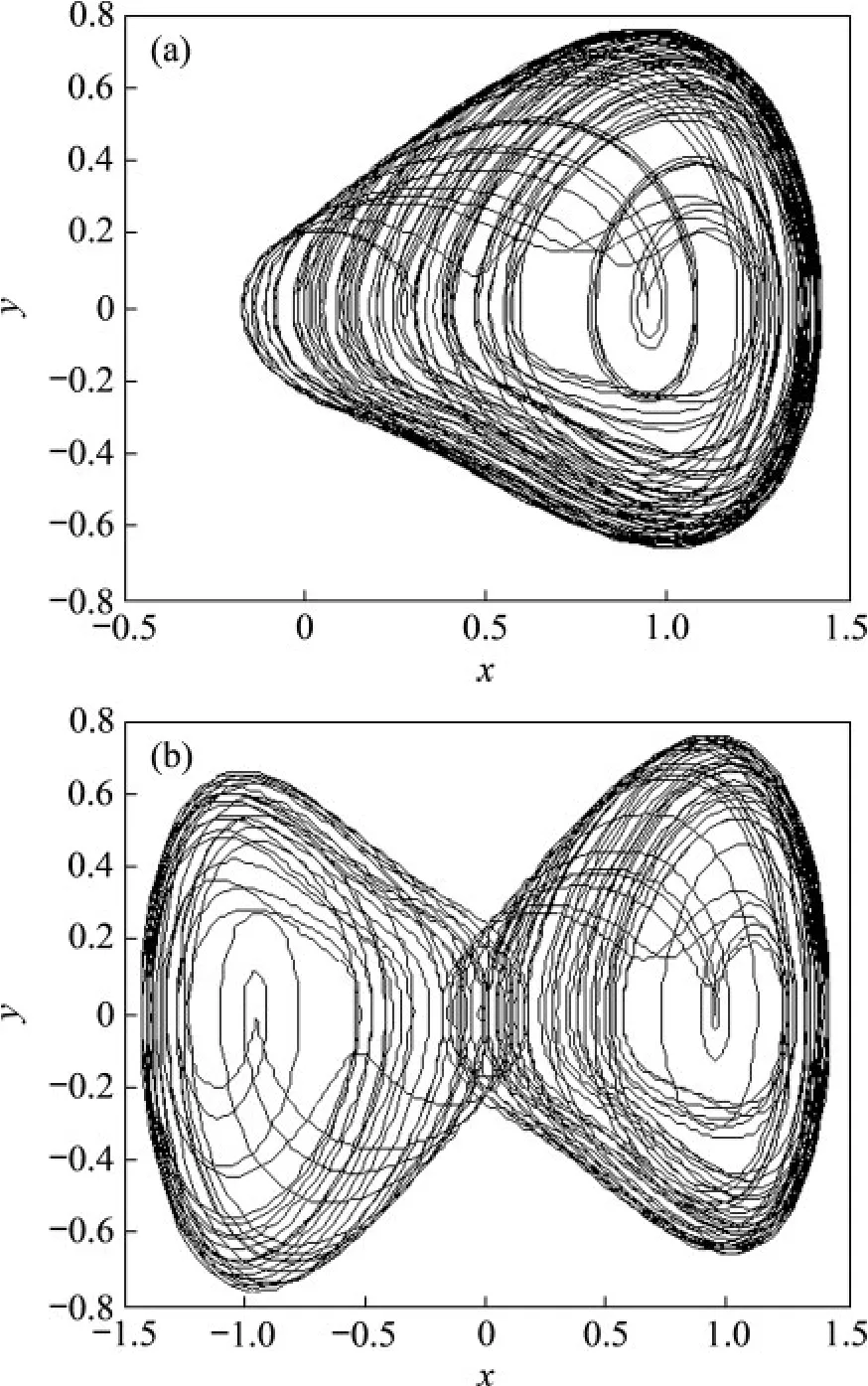
圖2 Duffing振子x-y相圖Fig.2 x-y plane of Duffing oscillator

Duffing 振子x-y 相圖如圖2 所示。由圖2 可知：參數f在由0逐漸增大至0.382的過程中，狀態變量x 的值域未發生突變，x-y 相圖未發生明顯變化；當f 由0.382 增加到0.383 時，x-y 相圖顯示出Duffing 振子的吸引子形狀發生了明顯變化，狀態變量x的值域出現了階躍性變化。因此，可以通過觀察Duffing 振子吸引子發生了階躍變化，得出混沌系統的參數發生變化的結論。將Duffing 振子吸引子的形狀變化作為待測信號存在同頻諧波信號的判斷依據具有可行性。

1.2 Lorenz振子的吸引子階躍變化現象

Lorenz 系統為典型自治混沌系統，不顯含時間和頻率。利用文獻[13]提出的非共振參數周期信號強迫Lorenz 系統，控制混沌狀態變化思想，設計基于Lorenz振子的微弱信號檢測模型如下：

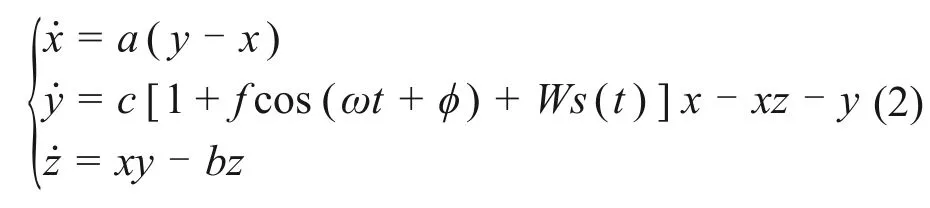
式中：1+ f cos(ωt + φ)為強迫信號。對于Lorenz系統，多數研究設定a=6.4，b=8/3，當0 ＜c ＜1時，系統穩定于原點；當1 ＜c ＜24.74時，系統處于不穩定狀態；當c ＞24.74 時，系統處于穩定的混沌或周期狀態[19]。因此，設定Lorenz系統參數為a=6.4，b=8/3，c=25.4，ω=60 rad/s，考慮輸入信號s(t) = 0。圖3 所示為變量x 隨參數f 變化的Lorenz振子局部分岔圖。由圖3可知：隨著參數f的變化，狀態變量x的值域發生了幾次明顯的階躍性跳變。

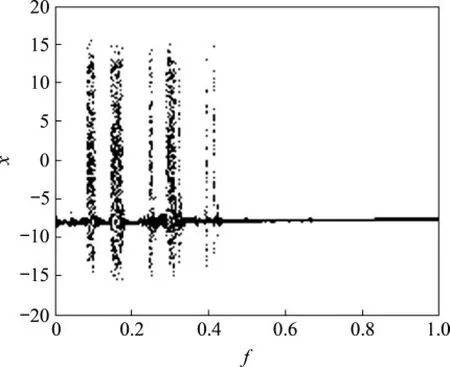
圖3 Lorenz系統局部分岔圖f ∈[0,1]Fig.3 Local bifurcation diagram of Lorenz system f ∈[0,1]

Lorenz振子x-z相圖如圖4所示。由圖4可知：參數f 在臨界點f =0.149 的前后變化時，Lorenz 振子的x-z相圖的混沌吸引子形狀發生了較明顯的變化，Lorenz 振子的吸引子的變化同樣具有參數敏感性，因此可以將Lorenz 振子吸引子的階躍變化作為待測信號存在同頻諧波信號的判斷依據。

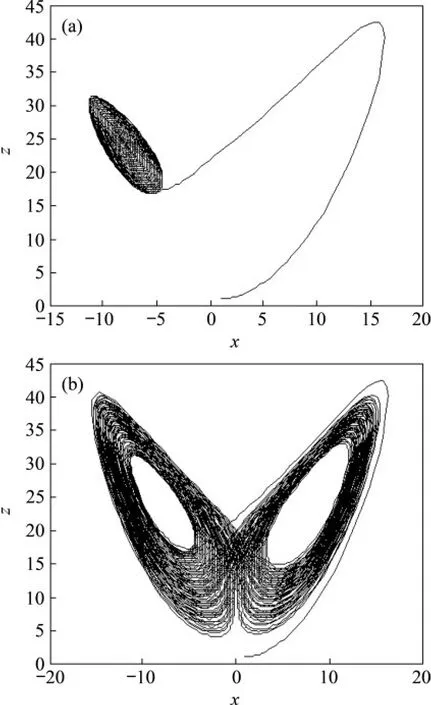
圖4 Lorenz振子x-z相圖Fig.4 x-z plane of Lorenz oscillator

對2類典型的混沌系統的動力學特性進行分析后發現，隨著特定參數的變化，當參數超過某一臨界值時，Duffing 振子和Lorenz 振子都存在吸引子發生階躍變化的現象，可以通過觀察吸引子發生階躍變化判斷系統參數發生變化。這一結論為基于混沌吸引子階躍變化的微弱信號檢測方法的可行性提供了理論支持。

2 微弱信號檢測方法

基于混沌吸引子階躍變化的微弱信號檢測分為3個階段：第一階段是混沌系統選取，即選取合適的混沌振子，設計相應信號檢測系統；第二階段是系統調整，即確定閾值將系統調整到某一臨界狀態；第三階段是輸入待測信號，選取合適的判斷依據，判斷待測信號成分是否存在。具體檢測流程如圖5所示。

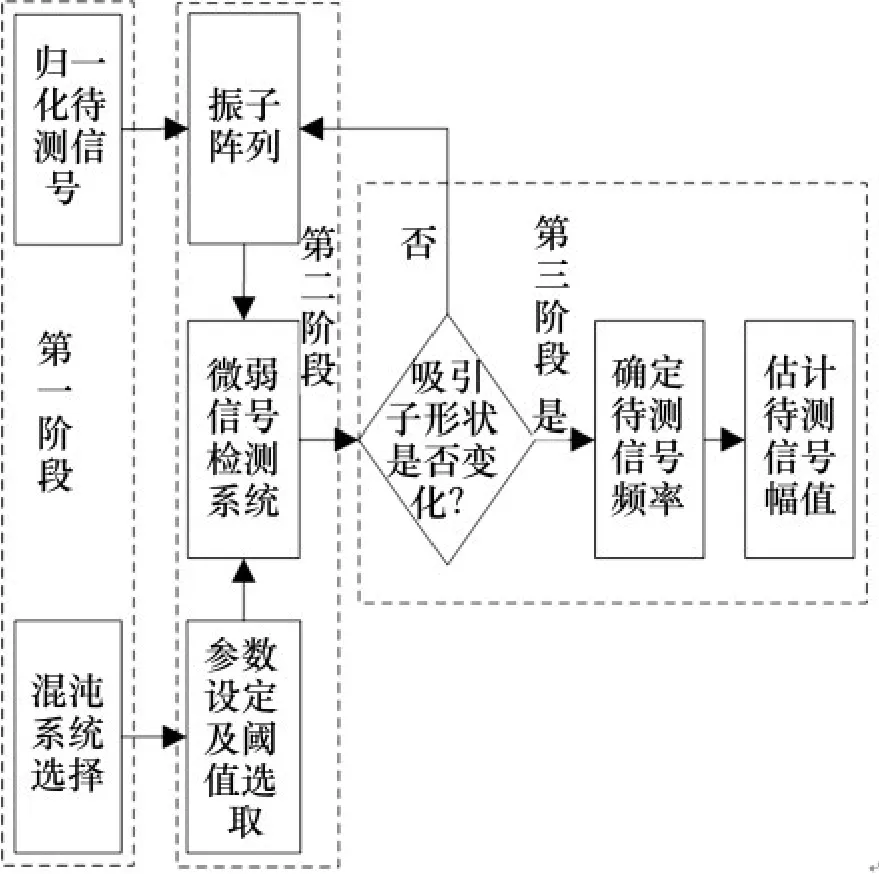
圖5 檢測流程圖Fig.5 Detection flow chart

在第一階段，選取混沌振子。根據混沌振子的動力學特性，確定固定參數與變化參數后設計相應的微弱信號檢測系統。然后對待測信號進行預處理，為避免含噪信號對檢測系統的影響，利用待測信號的最大瞬時幅值預估待測信號強度，將信號進行歸一化處理，與加權因子結合，使信號強度降低到0.01 W以下。

在第二階段，調整系統。由于強迫力的頻率變化對系統的動力學特性影響較明顯，因此采用固定強迫力頻率，引用變尺度的思想對待測信號進行時間尺度或頻率尺度的縮放，變尺度是在不改變信號離散數值的前提下，在時間或頻率軸上重排待測信號[14]，將高頻信號轉換為任意頻率的低頻信號。然后在當前參數條件下確定臨界狀態的閾值。最后調整系統處于臨界狀態。

在第三階段，將預處理后的待測信號輸入檢測系統中，根據吸引子的變化情況檢測輸入信號是否含有待測頻率成分。若吸引子發生變化，可確定待測信號包含當前頻率的諧波成分。

2.1 變尺度方法

設待測信號的角頻率為ω1，采樣角頻率為ωs，則混沌振子數值計算的步長為2π/ωs。變換龍格-庫塔數值計算的步長可以實現待測信號時標的擴張[14]，變換系數設為R，則計算步長為2πR/ωs。通過尺度變換可以將待測信號變化為頻率為ω1/R 的信號，將信號輸入處于臨界狀態的混沌振子中，若R = ω1/ω，則混沌陣子的吸引子會發生階躍變化。由此可判斷待測信號存在特定頻率成分，待測信號頻率ω1可通過強迫項頻率ω 與R 的乘積獲得。改變R可在固定強迫力角頻率的條件下，檢測信號是否含有待測成分。

2.2 閾值自適應選取方法

在實驗過程中發現閾值的選取對檢測結果的影響也比較明顯，精度高的閾值能夠提高檢測系統的分辨力，但是，由于噪聲的不確定性，在沒有待測頻率的信號時，強噪聲也可能誘導混沌吸引子發生變化。在同等強度的噪聲背景影響下，閾值的精度較高，其容噪性和保厚性都會下降，導致檢測結果的正確率降低。因此，閾值選取需要滿足所對應的混沌系統臨界點的突變性和敏銳性，臨界點的鄰接區間必須保持一定的厚度，同時閾值也要有一定的容噪性[15]。目前大部分基于混沌振子的微弱信號檢測都存在檢測閾值難以確定的問題。本文以混沌吸引子的階躍性變化作為判斷依據，提出一種自適應選取閾值的方法。

以基于Duffing 振子混沌吸引子形狀階躍變化的方法進行微弱信號檢測為例，參數選取與1.1節的相同。觀察Duffing 振子的局部分岔圖與圖6 所示的吸引子形狀發生階躍變化前后時域波形圖，發現當f=0.382時，吸引子形狀沒有發生明顯變化，時域波形圖中狀態變量x 全部大于-0.2。而當f=0.383 時，吸引子形狀發生明顯階躍變化，狀態變量x有一部分小于-0.2，x的值域發生明顯變化。

以此為依據，設計閾值自動選取方法。檢測系統初始參數設置與1.1 節相同，閾值為fd。檢測強迫力頻率不等的待測信號的頻率時需要對待測信號進行尺度變換，當變換系數R 超過一定范圍時，待測信號的采樣間隔和數值計算步長變化過大，有可能使檢測振子的動力學特性發生變化，檢測正確率也會下降。閾值自適應選取，由初始值開始，步長取2πR/ωs，增加參數f。用龍格-庫塔法求解當前參數條件下的Duffing 方程，得到狀態變量x解集。xd為判斷吸引子發生變化的狀態變量閾值，N為當前參數條件下，狀態變量值域超過閾值連續出現的次數，M 為狀態變量值域不超過閾值的狀況連續出現次數。初始設定N=0，M=0，xd=-0.2。判斷解集中是否有小于xd的x，若求解Duffing 系統有小于xd的x，則設定N=N+1，M=0；若沒有，則設N=0，M=M+1。繼續判斷N 和M 是否滿足都大于等于20，若滿足，則f-20(2πR/ωs)可作為檢測系統的閾值fd。實現自適應選取當前參數條件臨界閾值，具體流程圖如圖7所示。

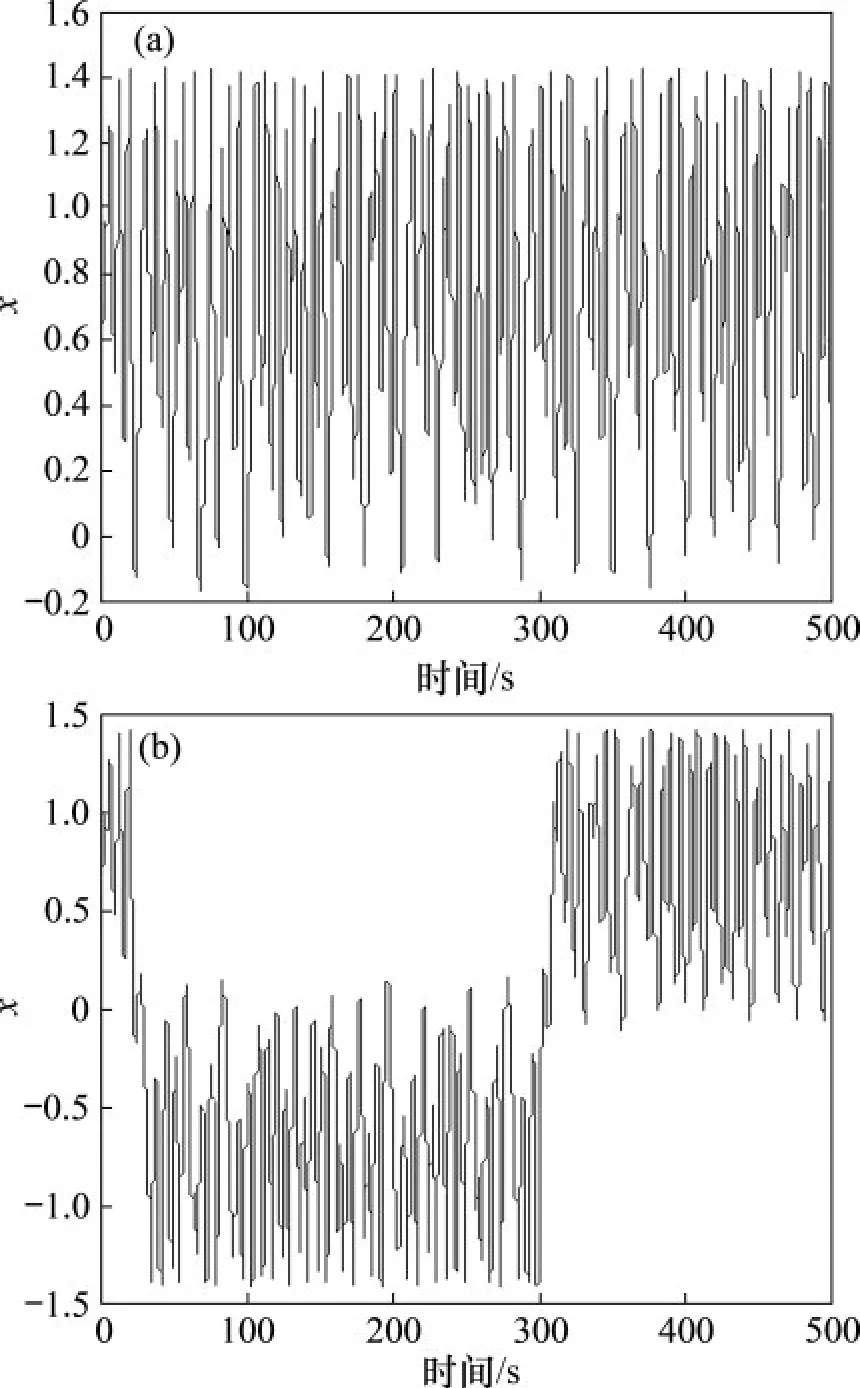
圖6 x的時域波形圖Fig.6 Time domain waveform of x

2.3 混沌吸引子階躍變化自動判斷方法

閾值確定后，將待測信號輸入Duffing 微弱信號檢測系統中，若含有與強迫力頻率相同成分，則系統的吸引子形狀發生變化。檢測系統在臨界狀態時域波形圖中，狀態變量x 的取值都大于-0.2，超過臨界狀態，有一部分x 小于-0.2。可將-0.2 作為判斷混沌吸引子發生階躍變化的閾值xd。將待測信號輸入微弱信號檢測系統，判斷狀態是否有小于xd的變量x出現，用矩陣變量C表征對應混沌振子吸引子形狀是否發生變化，若發生變化，則C(i) = 1，否則，C(i) = 0(其中，i 為混沌振子序列號)。建立待測頻率與吸引子發生階躍變化對應關系表，可直接給出判斷結果。

2.4 檢測盲區的消除

設f1為輸入信號中同頻諧波成分信號幅值，φ1為同頻諧波成分信號初始相位，Δω= ω- ω1為強迫力與待測信號的頻差。Δφ= φ- φ1為強迫力與待測信號的相位差。總強迫力為

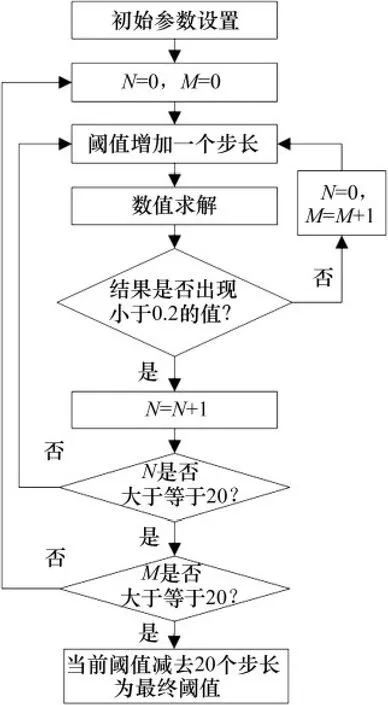
圖7 算法流程圖Fig.7 Detection flow chart

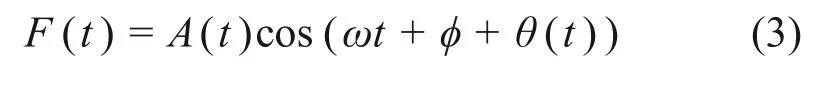
其中：

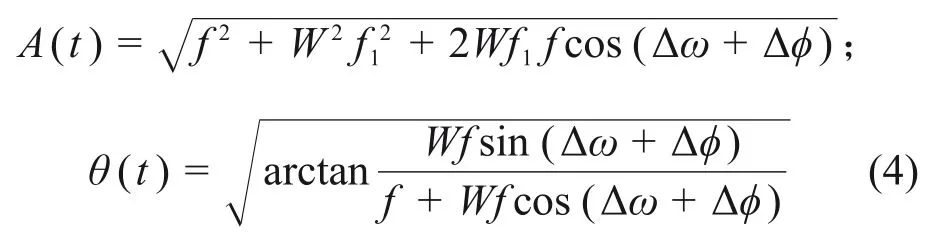
Duffing 系統強迫力與參考信號相位差范圍為[-arctan(Wf1/fd),arctan(Wf1/fd)]。由于加權因子的存在，強迫力的幅值f 遠大于待測信號的幅值Wf1，因此待測信號相位對系統的影響可以忽略。

系統處于臨界狀態時，將fd代入式(4)得

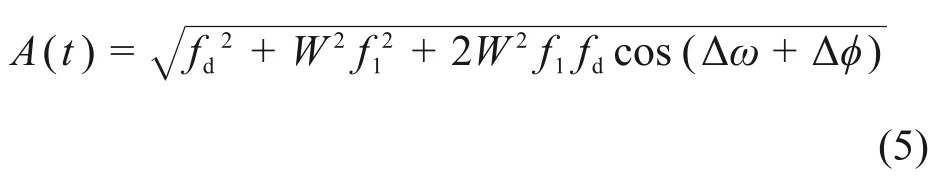
只有當A(t) ＞fd時，混沌系統的吸引子形狀才會發生變化。此時，Duffing 系統檢測窗口為[-π + arccos(Wf1/(2fd)),π - arccos(Wf1/(2fd))]。為消除檢測盲區，需對沒有產生吸引子變化的輸入信號進行系統周期強迫力移相π 后的二次檢測[16]，確保不會出現因初始相位的不同產生的漏檢現象。

3 仿真信號檢測

根據基于混沌系統吸引子階躍變化的檢測方法的原理，若待測信號中含有強迫力同頻成分，總的強迫力的幅值超過閾值引起系統吸引子形狀發生突變。為驗證該方法的有效性，利用如式(6)所示模型[17]模擬滾動軸承內圈早期故障，作為輸入信號輸入檢測系統。

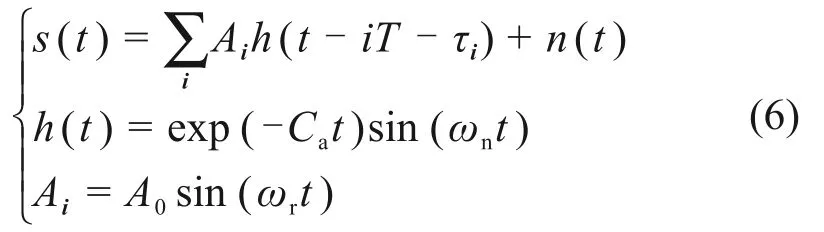
式中：s(t)為周期性成分；A0為其幅值，取值0.4；n(t)為功率可調整的白噪聲，疊加噪聲后信噪比為-43.6 dB；ωr為轉動角速度，取值40π rad/s；Ca為衰減系數，取值500；ωn為共振角速度，取值為7 000π rad/s；特征頻率為100 Hz，特征角頻率為ωi=200π rad/s；τi為相對于周期T的第i次沖擊造成的微小隨機波動，服從標準差為5%ωr的正態分布；采樣角頻率ωs設106π rad/s。圖8所示為滾動軸承內圈故障仿真信號波形及頻譜，由于仿真軸承故障信號相對背景噪聲較為微弱，圖8(c)所示的頻譜圖中內圈故障特征頻率并不突出，因此不能通過頻譜分析判斷故障類型。對仿真信號進行包絡譜分析，如圖9所示，未見明顯的特征頻率成分。

利用Duffing 和Lorenz 微弱信號檢測系統對仿真信號進行檢測，設置輸入信號的加權因子W=0.005，2個檢測系統的參數與第1.1節和1.2節中的一致。由于待測成分已知，將故障特征頻率作為待測信號的頻率，即ωi=ω1。可根據第2.1 節的尺度變換方法對待測信號進行變換。利用Duffing 系統檢測內圈故障特征角頻率的1 倍頻和2 倍頻時，R 分別設為623.319 與1 256.637；利用Lorenz 系統檢測時，R分別設為10.472與20.944。在當前步長條件下自動選取閾值，將Duffing 和Lorenz 微弱信號檢測系統調整到臨界狀態。將尺度變換后的s(t)輸入各系統進行檢測，圖10～13所示為混沌振子的相圖。

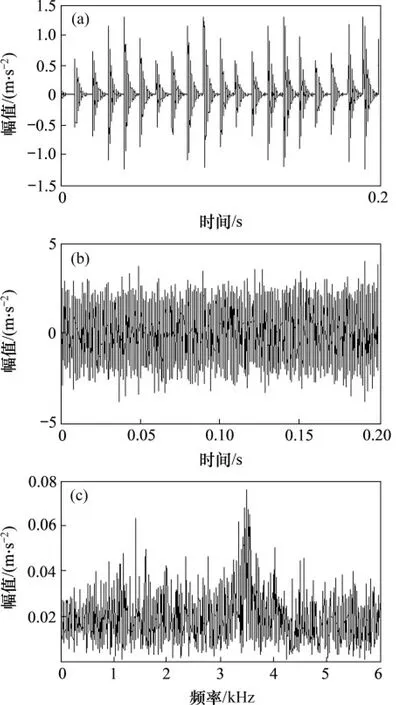
圖8 仿真信號的波形及頻譜Fig.8 Waveform and spectrum of simulated signal

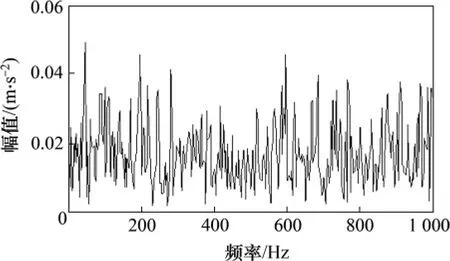
圖9 仿真信號的包絡譜Fig.9 Envelope spectrum of simulated signal

用龍格-庫塔法對各系統進行數值求解，得到狀態變量的集合。在對輸入Lorenz 系統的信號求解后得到關于狀態變量x的解集后，去掉前期部分數據，判斷剩下的解集中是否有超出閾值xd的解出現，Lorenz系統的xd=0。若有，則自動判定待測頻率信號的存在。通過判斷吸引子形狀是否發生階躍變化，判定待測信號是否含有特定成分。記錄檢測結果。表1 所示為Duffing 和Lorenz 系統的參數閾值設置與檢測結果。

圖10 Duffing振子x-y相圖(R=623.319)Fig.10 x-y plane of Duffing oscillator(R=623.319)

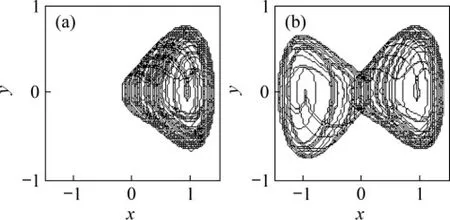
圖11 Duffing振子x-y相圖(R=1 256.663)Fig.11 x-y plane of Duffing oscillator(R=1 256.663)

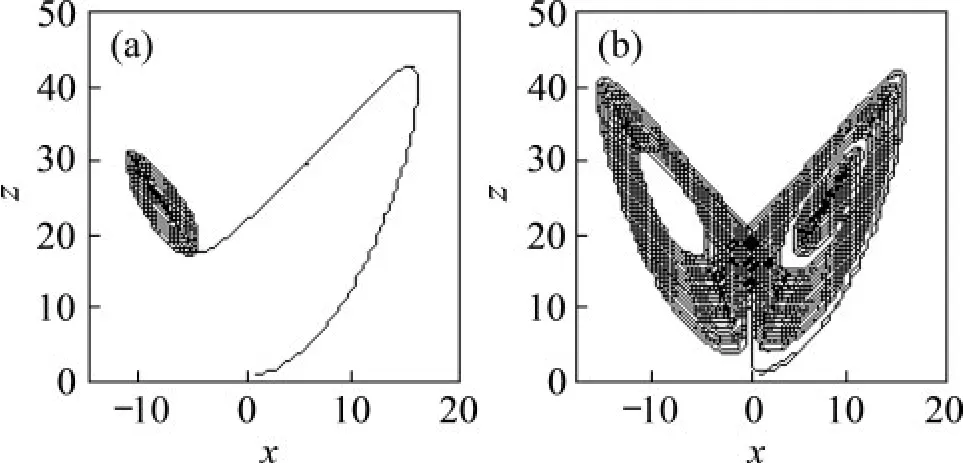
圖12 Lorenz振子x-z相圖(R=10.472)Fig.12 x-z plane of Lorenz oscillator(R=10.472)

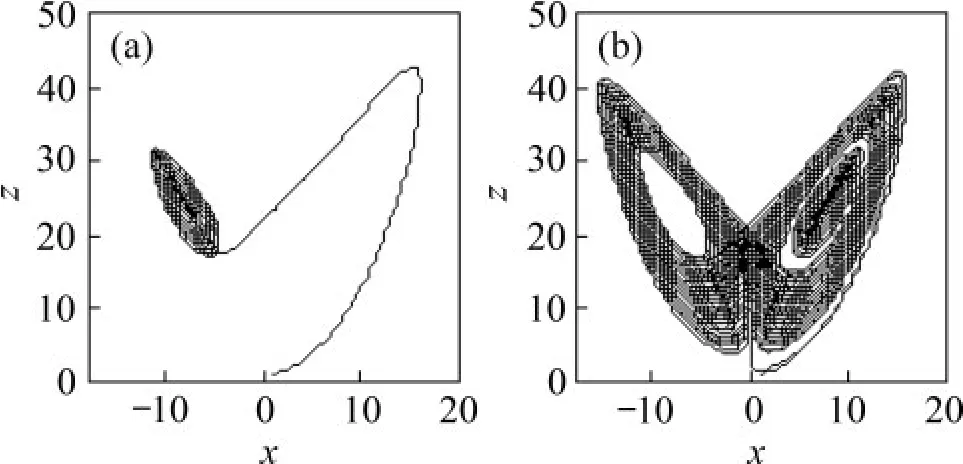
圖13 Lorenz振子x-z相圖(R=20.944)Fig.13 x-z plane of Lorenz oscillator(R=20.944)

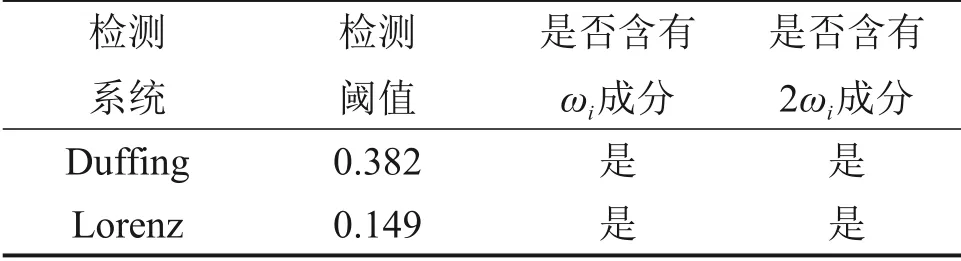
表1 參數閾值設置與檢測結果Table 1 Threshold and detection results for simulated signal

從表1可以看出：采用基于混沌吸引子的階躍變化進行微弱故障信號檢測，Duffing 系統和Lorenz 系統都能檢測出滾動軸承內圈故障特征角頻率成分。結果表明，Duffing 系統和Lorenz 系統在對不同頻率的信號進行檢測時的容噪性都比較穩定，檢測正確率相對較高；Lorenz 系統的求解過程時間都比稍長，Duffing系統的求解用時較短。

4 實驗信號檢測

為進一步驗證本文方法有效性和實用性，利用電火花分別在SKF6205 軸承外圈、內圈上人工植入深度為1.5 mm，寬度為0.2 mm 左右的微小凹痕，將故障軸承安裝在QPZZ-Ⅱ實驗裝置上模擬滾動軸承早期微弱故障。利用電機帶動傳動軸模擬在軸承處于早期微弱故障狀態下的機械運轉情況，軸承轉動速度為1 470 r/min。利用加速度傳感器采集故障信號，采樣頻率為12 kHz。

表2所示為故障軸承的結構參數。計算可得在當前軸承參數與轉速條件下滾動軸承外圈故障的征頻率為87.8 Hz，滾動軸承內圈故障特征頻率為132.6 Hz。

表2 故障軸承結構參數Table 2 Structural parameters of fault rolling bearing

4.1 外圈故障檢測

分析歸一化處理后的外圈故障信號，圖14 所示為信號時域波形圖與頻譜圖。由于軸承故障損傷相對微弱，頻譜中沒有發現與外圈故障特征頻率相關的成分。外圈故障包絡譜圖15所示。可見，未發現突出的外圈故障特征頻率，因此不能通過頻譜分析和包絡譜分析判斷實測信號的故障類型。

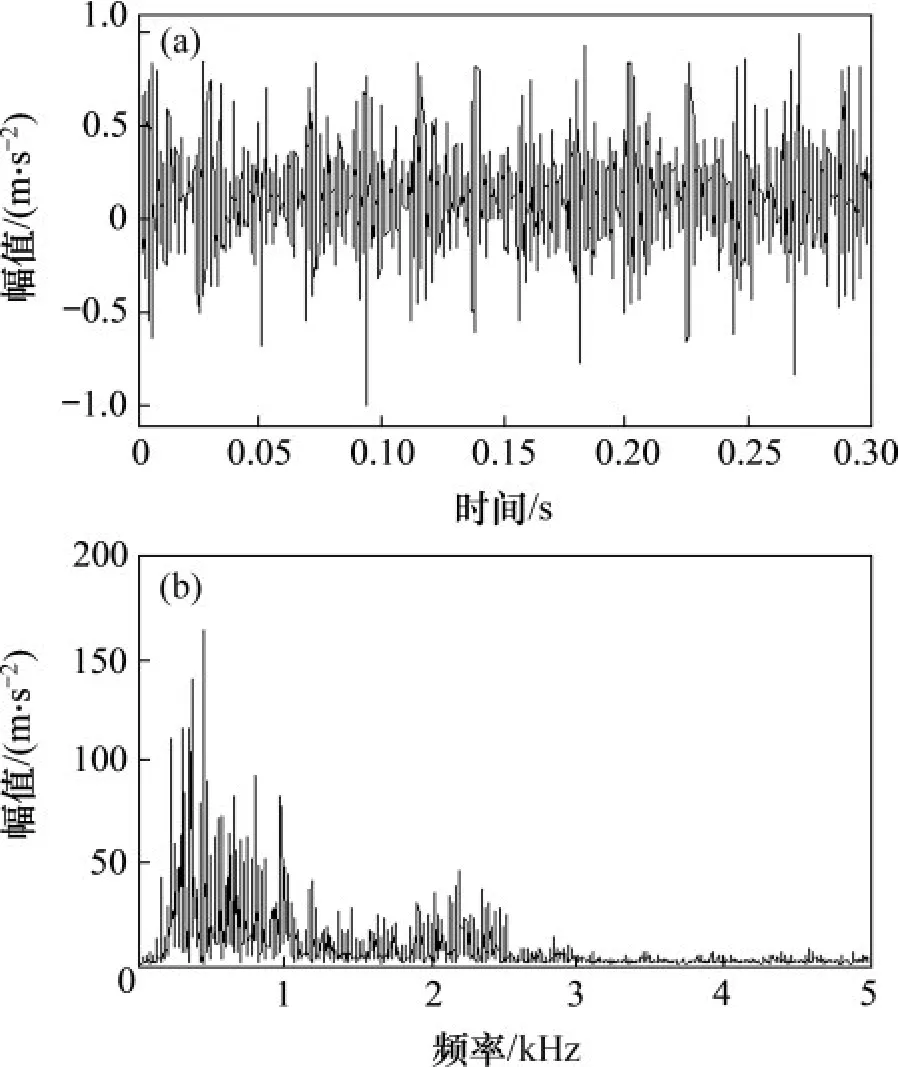
圖14 外圈故障時域波形圖及頻譜圖Fig.14 Time domain waveform and spectrum diagram of outer race fault

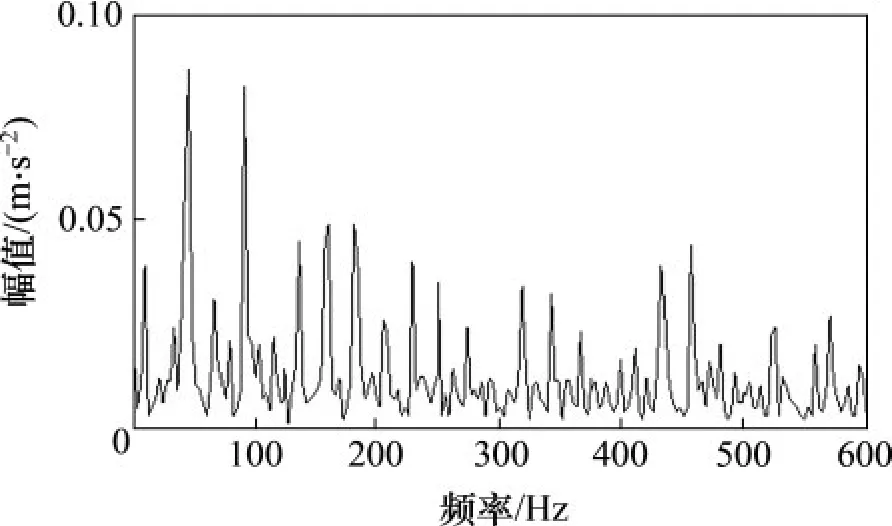
圖15 外圈故障信號包絡譜Fig.15 Envelope spectrum of outer race fault signal

利用本文方法對實測信號進行分析，計算滾動軸承外圈故障的特征角頻率約為551.8 rad/s，實驗過程中發現Lorenz 混沌振子在檢測高頻信號方面表現出更好的容噪性，因此，選Lorenz 混沌系統作為混沌振子，系統參數與1.1節中的一致，利用自適應閾值選取方法確定閾值fd=0.149。將歸一化后的信號進行R 尺度變換，R=ωi/60，為避免特征頻率因軸承參數與計算精度等原因造成計算誤差，外圈特征角頻率ωi∈[ωi- 5,ωi+ 5]，使ωk+1= ωk+ 0.5，k 為檢測振子序號，共20 個振子。在對外圈故障的特征角頻率的2倍頻進行檢測時，ωi= 1103.6 rad/s，其他參數不變。Lorenz 混沌振子微弱信號檢測系統調整到臨界狀態，將經尺度R 變換后的信號輸入檢測系統，步長為R/12 000。根據混沌吸引子的變化特點，若發生變化，則C(i) = 1，否則C(i) = 0。檢測結果由吸引子形狀隨待測頻率的變化曲線表示，如圖16所示。

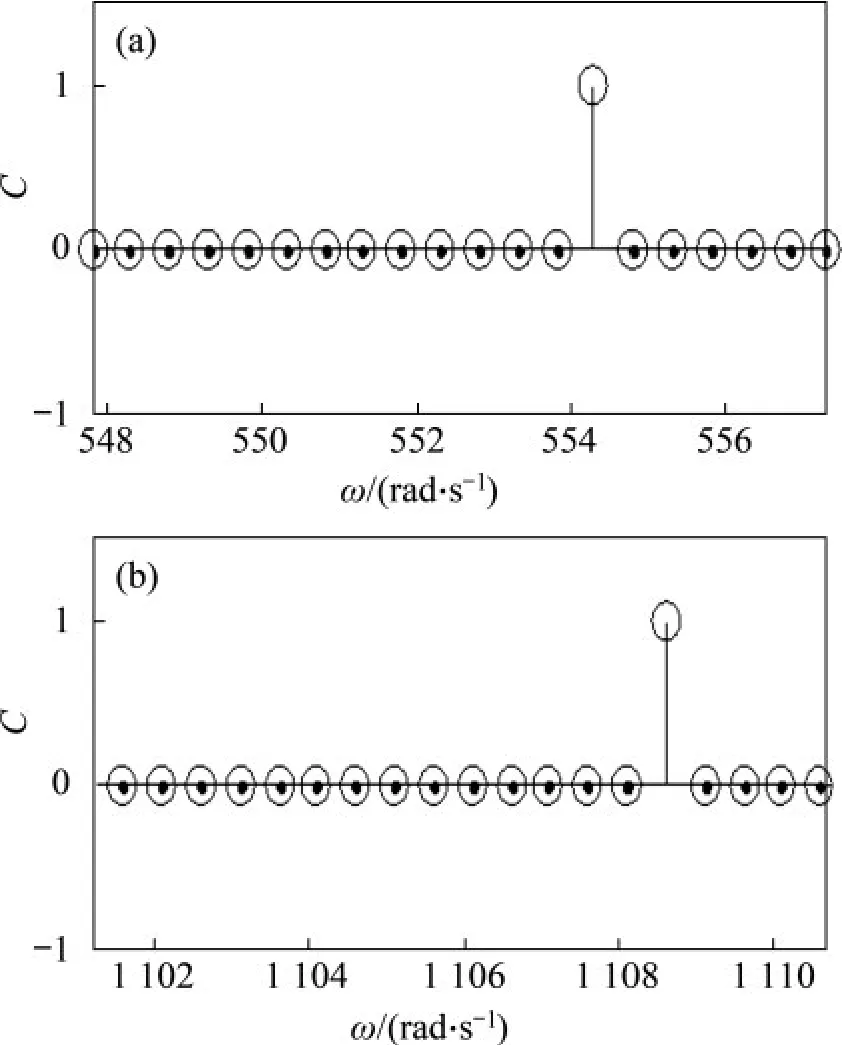
圖16 外圈故障檢測結果Fig.16 Detection results of outer race fault

待測外圈故障信號的特征角頻率實測值約為554.2 rad/s，2 倍頻約為1 108.6 rad/s。特征頻率約為88.2 Hz 和176.4 Hz，在轉速與環境等因素影響下，理論值與實測值有一定偏差。特征角頻率的計算值與實測值非常接近，說明本文方法能夠檢測滾動軸承外圈微弱故障。

4.2 內圈故障檢測

對內圈故障實測信號歸一化后進行分析，圖17 所示為信號的時域波形圖與頻譜圖。可見頻譜圖中內圈故障特征頻率同樣不明顯。圖18 所示為內圈故障包絡譜。可見，未發現含故障特征頻率成分。因此不能通過頻譜分析和包絡譜分析判斷實測信號的故障類型。

利用4.1 節的混沌振子對實測信號進行檢測。經計算，內圈特征角頻率約為833.2 rad/s，設內圈特征角頻率取值為827.7～837.7 rad/s， 間 隔0.5 rad/s，共20個值，將歸一化后的信號進行R尺度變換，R為ωi/ω。檢測結果由吸引子形狀隨待測頻率的變化曲線表示，如圖19所示。

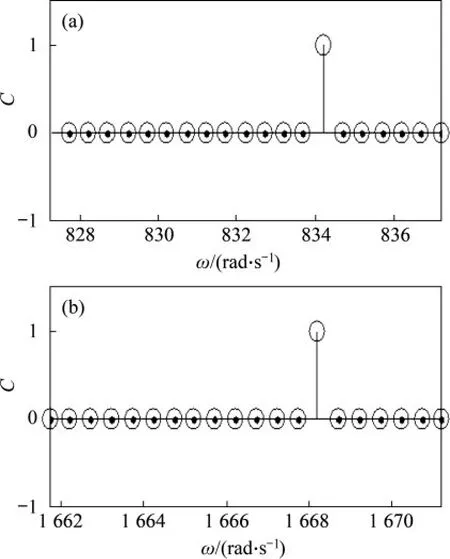
圖19 內圈故障檢測結果Fig.19 Detection results of inner race fault

經檢測待測信號的故障頻率約為834.2 rad/s，2 倍頻約為1 668.2 rad/s。特征頻率的1 倍頻與2 倍頻分別約為132.8 Hz和265.5 Hz，接近計算值。結果表明：本方法能夠從實測信號中準確地檢測出滾動軸承內圈故障的特征頻率。

5 結論

1)隨著參數的改變，Duffing 振子和Lorenz 振子都存在吸引子發生階躍變化的現象。提出一種基于吸引子形狀階躍性變化的微弱信號檢測方法。通過設計自適應的選取檢測閾值方法和自動檢測吸引子形狀變化的方法，無需觀察相圖，自動判定信號中待測成分的存在。

2)本文方法能夠有效檢測滾動軸承微弱故障信號的特征頻率成分，易于工程實現。為基于混沌系統的微弱諧波信號檢測一種提供了有效的定量分析新方法，在微弱故障信號故障診斷中具有實際應用價值。