基于改進PID 算法的干擾設備控制方法研究

黃宗衛(wèi)，范 越

（中國船舶重工集團公司第七二三研究所，江蘇揚州 225001）

0 引言

干擾設備主要是指對敵方電子儀器和電子系統(tǒng)實行電子干擾，使之喪失或降低效能的設備，其伺服控制系統(tǒng)主要功能是實現(xiàn)干擾設備本身空域穩(wěn)定，能夠對處于移動狀態(tài)的干擾動目標進行連續(xù)有效地干擾。為了實時高效地對敵對目標實施干擾，要求伺服控制系統(tǒng)具有較高的跟蹤精度與快速的動態(tài)性能，快速動作、精確指向。對于傳統(tǒng)的PID控制算法，需要有較大的控制增益才能實現(xiàn)快速的動態(tài)性能與較高的跟蹤精度，但是在調(diào)舷過程中或者初始誤差較大時，大的比例增益會出現(xiàn)超調(diào)過大，降低系統(tǒng)的穩(wěn)定性，傳統(tǒng)的PID 算法不能同時滿足精度與穩(wěn)定性的要求［1-2］。傳統(tǒng)PID 控制算法參數(shù)整定簡單，但只能針對特定單一的被控對象和性能指標需求。在實際應用過程中，由于被控對象的自身特性（時變、非線性）以及外界隨機噪聲的干擾，固定的控制參數(shù)難以同時滿足控制精度及穩(wěn)定性的要求。在跟蹤雷達的伺服控制過程中，為了提高跟蹤精度與快速性，需要較大的比例增益，但大的比例增益會降低系統(tǒng)穩(wěn)定性，尤其在跟蹤雷達開始工作時若存在調(diào)舷的動作，會引起超調(diào)，若調(diào)舷幅度較大，超調(diào)量會超出相應的閾值。本文提出一種改進的PID 控制算法，設計可變的比例系數(shù)P，既能滿足設備啟動時的穩(wěn)定性，又能提高跟蹤過程中的控制精度。

1 干擾設備伺服系統(tǒng)工作原理

伺服控制系統(tǒng)是干擾設備的重要組成部分，利用編碼器實時測量干擾設備指向角度，并根據(jù)控制指令計算與目標之間的誤差，經(jīng)過控制算法運算之后控制伺服電機進行動作，實現(xiàn)干擾設備天線的對準和對移動目標的跟蹤［3］。干擾設備伺服控制系統(tǒng)采用三環(huán)控制策略，主要包括電流環(huán)、速度環(huán)、位置環(huán)三個部分。電流環(huán)及速度環(huán)選擇由高性能的電機及驅動器集成，可以有效抑制電機參數(shù)時變、非線性和反電動勢的影響，提高執(zhí)行機構的動態(tài)及穩(wěn)態(tài)性能；位置環(huán)由編碼器、位置控制器、伺服被控對象組成，完成控制指令的接收、位置信息的采集、誤差處理與運算，從而實現(xiàn)干擾設備伺服系統(tǒng)的隨動和精確跟蹤。干擾設備伺服控制系統(tǒng)組成框圖如圖1所示。

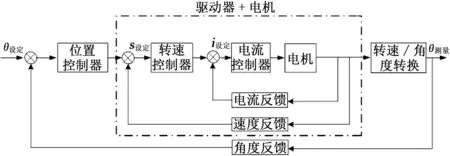
圖1 伺服控制系統(tǒng)方框圖

2 改進PID算法

傳統(tǒng)PID控制算法包括比例、積分和微分環(huán)節(jié)，是典型的線性控制方法，結構簡單，在伺服控制領域應用廣泛。

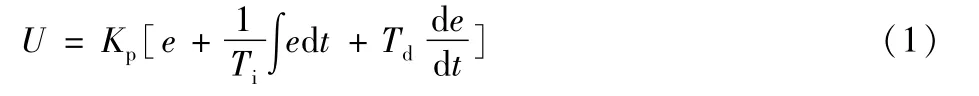
式中：U為控制器輸出；e為誤差，即設定值與實際值的差；Kp、Ti、Td分別為比例系數(shù)、積分時間常數(shù)、微分時間常數(shù)。

比例控制是最簡單的控制方式，控制器輸出與輸入成正比，僅有比例控制時系統(tǒng)存在穩(wěn)態(tài)誤差，誤差大小與控制器比例系數(shù)成反比。積分控制時，控制器輸出與輸入的積分成正比，可以有效消除系統(tǒng)的穩(wěn)態(tài)誤差。對于簡單的控制系統(tǒng)，比例-積分控制完全能夠滿足基本的控制性能要求，通過整定比例系數(shù)、積分系數(shù)實現(xiàn)相應的動態(tài)性能及穩(wěn)態(tài)精度要求。但是對于大慣性控制系統(tǒng)，在階躍響應作用下，偏差通常不會在短時間內(nèi)消除，積分項會造成較大的超調(diào)，嚴重甚至會引起系統(tǒng)震蕩，降低系統(tǒng)穩(wěn)定性。

在干擾設備伺服系統(tǒng)跟蹤模式下的工作過程中，為了快速調(diào)舷，實現(xiàn)對目標的跟蹤動作，提高跟蹤精度，需要較大的比例系數(shù)。雖然提高了動態(tài)性能與跟蹤精度，但會導致系統(tǒng)穩(wěn)定性降低，不能滿足控制系統(tǒng)的實際需求。本文介紹的改進型PID控制算法基于可變的比例系數(shù)，根據(jù)實時的誤差數(shù)值選擇比例系數(shù)，在誤差較大時選擇較小的比例系數(shù)，保持系統(tǒng)穩(wěn)定無超調(diào)；在系統(tǒng)誤差較小時，增大比例系數(shù)，提高跟蹤精度，其實質(zhì)是改變傳統(tǒng)PID控制算法線性控制器的特性，通過在線實時調(diào)整控制器比例系數(shù)，賦予控制系統(tǒng)非線性的特征，增強控制系統(tǒng)的魯棒性［4-6］。改進PID 控制算法原理框圖如圖2所示。

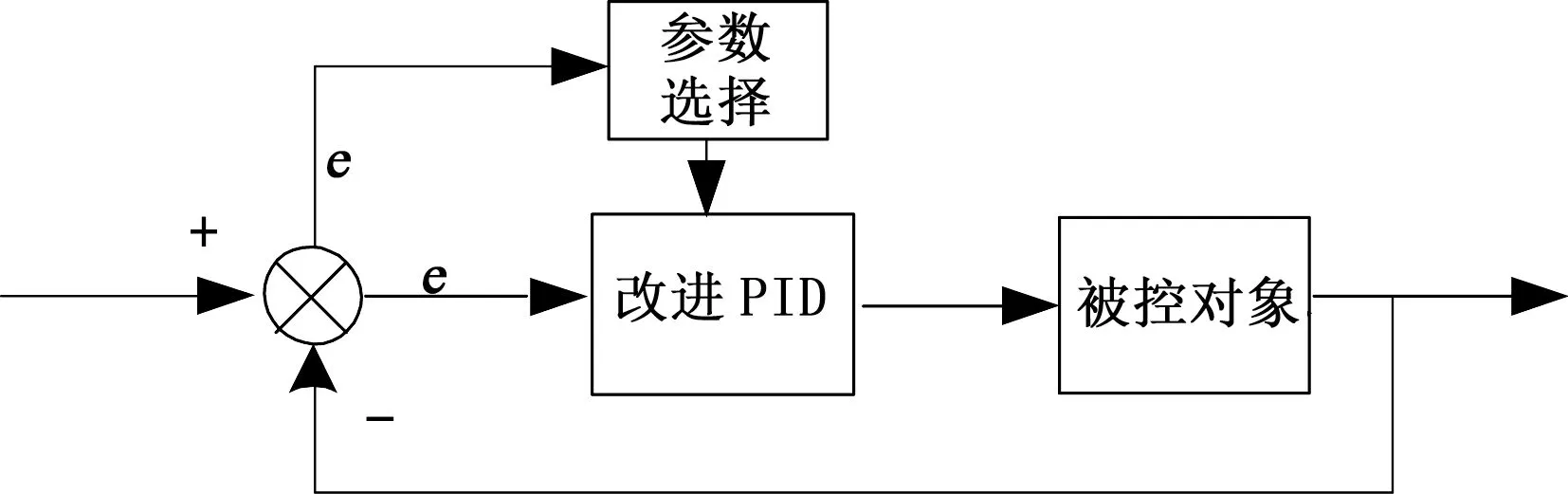
圖2 改進PID控制算法原理框圖

比例系數(shù)的具體選擇方法如圖3所示。當誤差絕對值大于m 時，比例系數(shù)Kp＝b；當誤差絕對值小于n 時，Kp＝a；當誤差絕對值介于n與m之間，比例系數(shù)隨誤差線性變化。比例系數(shù)上下限a與b具體數(shù)值的選擇需要根據(jù)實際調(diào)試與PID整定結果決定。數(shù)值a參考值選擇階躍信號無超調(diào)情況下的比例系數(shù)；數(shù)值b參考值選擇正弦信號跟蹤下誤差較小的比例系數(shù)。

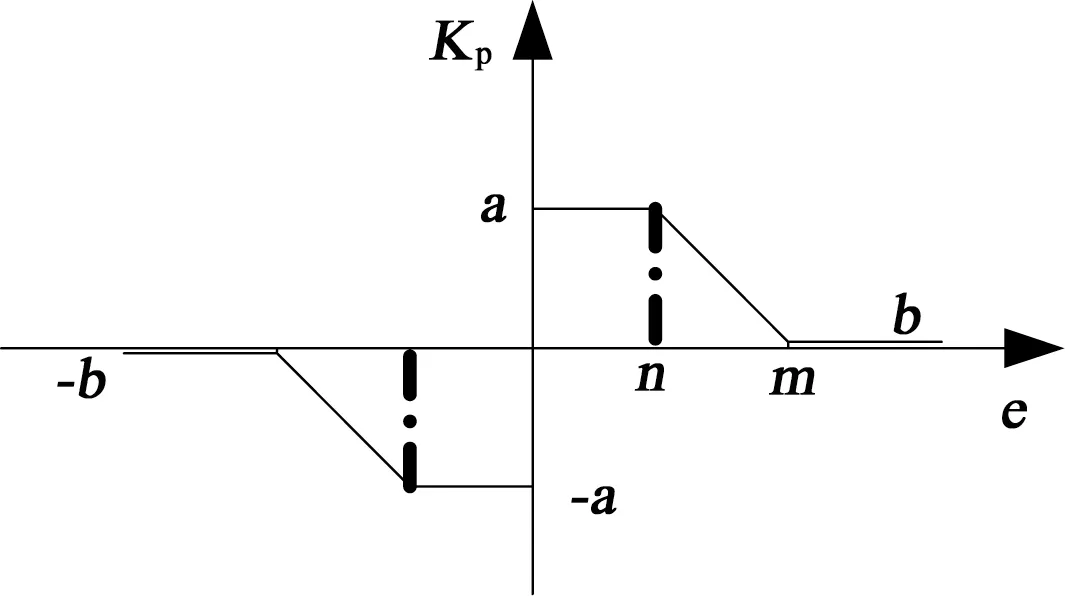
圖3 誤差與比例系數(shù)選擇關系

3 仿真測試及結果分析

干擾設備伺服控制系統(tǒng)的數(shù)學機理模型是一個比較復雜的高階非線性模型，其組成部分包括永磁同步電機（PMSM）、電機驅動器，伺服轉臺機械結構、減速器等都是典型的非線性模型。為了簡化設計流程，通過降階以及近似線性化處理，簡化為一典型的二階慣性環(huán)節(jié)。建立數(shù)學模型并基于MATLAB/simulink工具，分別設計傳統(tǒng)PID 控制算法與改進PID 控制算法進行仿真驗證［7-9］，對改進PID 控制算法控制性能進行研究分析，其仿真實驗模型如圖4 所示，仿真測試結果如圖5～6 所示。仿真實驗時，角度設定值選擇一固定周期的正弦曲線，周期1 s，變化幅度20°，模擬干擾設備實際工作情況下，實現(xiàn)快速調(diào)舷和跟蹤的工作狀態(tài)。

由仿真實驗結果可以看出，傳統(tǒng)PID控制算法難以兼顧動態(tài)跟蹤精度與穩(wěn)態(tài)性能，在滿足精度要求時，由于比例系數(shù)較大以及積分環(huán)節(jié)的存在，出現(xiàn)較大超調(diào)，若要繼續(xù)提高控制精度（即繼續(xù)增大比例系數(shù)），會降低系統(tǒng)穩(wěn)定性甚至導致系統(tǒng)震蕩。改進PID控制算法由于可以根據(jù)反饋誤差實時調(diào)節(jié)控制器參數(shù)，因此在階躍（模擬調(diào)舷）階段以及正弦跟蹤（模擬跟蹤）階段均具有較優(yōu)的動態(tài)性能與穩(wěn)態(tài)精度，增強了系統(tǒng)的魯棒性。

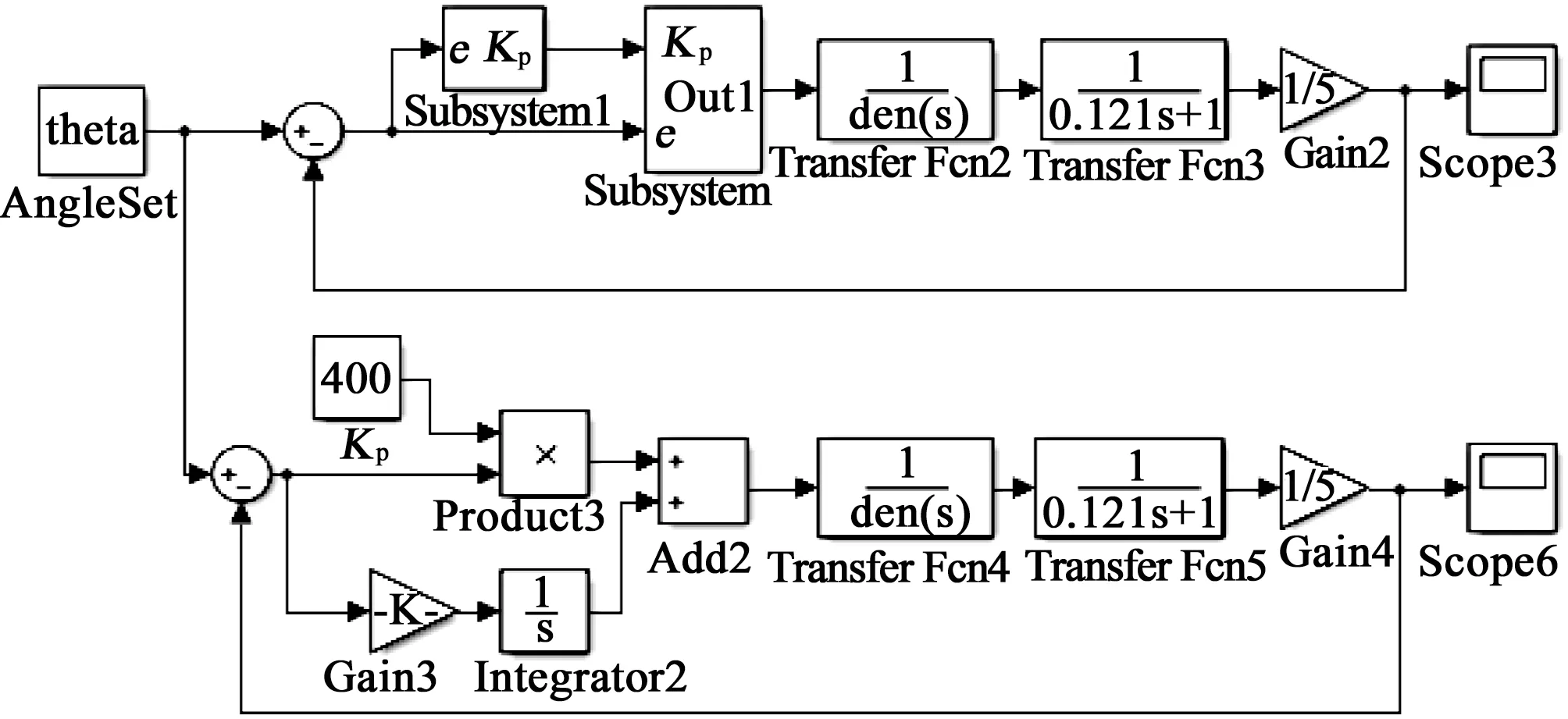
圖4 MATLAB/simulink仿真模型

圖5 傳統(tǒng)PID控制算法動態(tài)性能

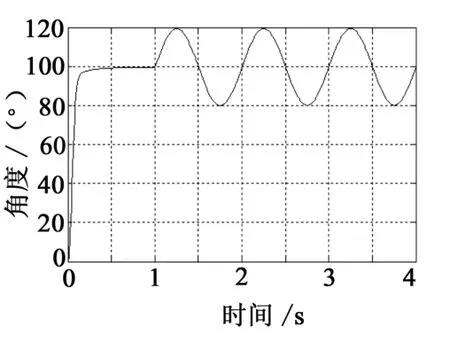
圖6 改進PID控制算法動態(tài)性能

4 結束語

本文研究了基于三環(huán)控制策略的改進PID 控制算法，該方法基于實時誤差在線調(diào)整控制器比例系數(shù)，在誤差較大時選擇較小的比例系數(shù)，保持系統(tǒng)穩(wěn)定無超調(diào)；在系統(tǒng)誤差較小時，增大比例系數(shù)，提高跟蹤精度，可以有效彌補傳統(tǒng)PID控制算法線性控制器特性單一的缺點，增強控制系統(tǒng)魯棒性，提高干擾設備伺服控制系統(tǒng)動態(tài)性能與穩(wěn)定精度，在工程上取得了良好的應用效果。