基于改進PCA-Logistic模型對個人汽車保有量預測
劉 斌,趙天舒,張冉霞
(大連海事大學 航運經濟與管理學院,遼寧 大連 116024)
0 引言
隨著我國經濟健康持續發展,社會收入水平不斷提高,城市化步伐逐漸加快,我國的個人汽車保有量在連年攀升[1]。個人汽車保有量是指公安交通管理部門按照《機動車注冊登記工作規范》,已注冊登記領有民用車輛牌照的全部私人汽車數量,也可以稱為私人或私家的汽車擁有量。根據《中國統計年鑒》[2-5],1985年我國個人汽車保有量只有約28萬輛,隨著改革開放的深入進行,我國汽車工業目前進入全面高速發展階段,2003年我國個人汽車保有量首次突破1 000萬輛。2006年,個人汽車保有量突破2 000萬輛,僅3年時間數量翻了一番。2013年我國個人汽車保有量突破了1億輛。截止到2018年,我國個人汽車保有量超過2億輛。
個人汽車帶給我們方便的同時,也為我們的生活帶來了一系列問題,如道路擁堵、交通事故頻發,停車困難、停車位昂貴,能耗嚴重、環境污染加劇,交通設施更替加速等。通過對個人汽車保有量的預測,可以為城市道路交通規劃工作的展開提供數據支撐,為政府對交通設施建設的投資成本預算提供依據[6]。
對于汽車保有量的預測,國外學者首先做了較多的研究,提出了許多模型,比如基于集合模型的Comperta模型[7]、基于非集合模型的多項Logit模型及多項Probit模型等,這些模型基于當地的人口、社會等數據信息,已經成功應用于發達國家。近年來國外學者也對印度等發展中國家汽車保有量建立模型進行了分析,Dash等提出分段線性多項Logit模型對印度個人汽車保有量進行了研究[8]。Shaygan等對伊朗的汽車保有量模型進行了綜述性分析,指出需要對已有模型進行更多改進才可適用于當地城市[9]。從中可以看出國外預測模型存在一定的區域性,由于國外汽車文化和經濟水平與國內相差較大,所以難以直接將其應用于國內的個人汽車保有量分析[10-11]。
國內的汽車保有量預測研究起步較晚,同樣也提出了許多模型與方法。陳勇和孔峰利用BP神經網絡建立了具有時間序列預測模型對我國私人汽車保有量進行了分析和預測[12]。朱開永等利用灰色系統理論建立私家車保有量預測模型對某地區1996—2007年私家車保有量分析[13]。張雪伍和常晉義通過主成分分析法將影響汽車保有量因子間的重復信息進行消除,建立了PCA-BP神經網絡預測模型對南京市1978—2005年的汽車保有量進行分析,并對未來南京市汽車保有量進行預測[11]。王傳鑫等基于改進密度峰值聚類方法研究了不同地區間私人汽車保有量影響因素的差異性,為研究的兩類地區私人汽車發展提供一定的參考[14]。蔣艷梅和趙文平建立了分別基于遺傳算法和非線性最小二乘法的Logistic模型,對我國汽車保有量進行了預測,并和其他文獻進行對比,結果表明Logistic模型預測私人汽車保有量的精確度比其他模型高[15]。張蘭怡和胡喜生等通過對影響汽車保有量的8個指標進行主成分分析,得到了綜合經濟發展值的預測方程,并采用Logistic模型預測福建省2020年汽車保有量[16]。任玉瓏等基于傳統Logistic模型和以灰色理論為基礎的極差格式的Logistic模型為基礎,建立了以誤差標準差為權重的Logistic組合模型對我國汽車保有量進行預測,得出了到2020年我國汽車保有量達到2.35億輛的結論[17]。
通過對國內外相關文獻進行整理可以發現,汽車保有量的發展趨勢比較符合隨時間變化呈S型變化的Logistic模型,同時許多研究都是通過分析影響汽車保有量的因素進行展開。主成分分析法可以通過“線性”降維技術將多個影響因素盡可能壓縮為少數幾個代表性綜合指標,再結合Logistic模型可以對汽車保有量進行分析和預測。但在實際應用中,影響因素可能存在非線性關系,尤其是對于時間跨度較長的數據,直接用傳統主成分分析的線性方法會影響降維效果,進而影響預測精度[18]。因此,本研究使用對數變換法對傳統主成分分析法進行了改進,結合Logistic模型,提出了改進PCA-Logistic模型,并對我國個人汽車保有量進行分析和預測。通過實證分析結果可以表明,改進PCA-Logistic模型可以消除數據之間的非線性影響,使得模型的模擬精度更高。
1 模型建立
1.1 改進的主成分分析法
傳統的主成分分析法是一種“線性”降維方法,如果變量間存在非線性關系,會導致降維效果不明顯,因此需要對傳統主成分分析法進行改進。常見的改進方法有均值法、對數變換法和平方根變換等,對原始影響因素數據進行分析,發現其隨著時間呈現類似指數形式的變化趨勢,于是改進方法采用對數變換法,以達到更好的降維效果。具體步驟如下[18]:
(1)對原始數據進行對數變換:設原始數據矩陣為X=(xij)n×p,令yij=lnxij,對數變換后矩陣為:Y=(yij)n×p,其中i=1,2,…,n;j=1,2,…,p。
(2)以yij作為新的數據代替原始數據,并對其進行標準化處理,以消除各個特征在數量級或量綱上的影響,公式如下:
(1)
式中,μ為各個指標數據的平均值;σ為各個指標數據的標準差。
(3)根據標準化矩陣,計算其協方差矩陣,計算公式為:
(2)
式中,c為協方差矩陣;n為數據指標的元素個數;Y*為標準化的數據。
(4)根據協方差矩陣計算特征值與特征向量,并將特征值從大到小進行排列。
(5)計算主成分貢獻率及累積貢獻率,并根據計算結果提取主成分。通常選取累積貢獻率在85%以上的對應成分作為主成分。
1.2 Logistic模型
Logistic方程由比利時數學家P.F.Verhulst在1838年首次提出,它是描述因變量隨時間變動趨勢的模型,能較好地描述某些呈現S型曲線增長的現象,并已經廣泛應用于農業、經濟學、醫學等領域。對于產品市場擴展分析,采用美國Edwin Mansfield提出的Logistic模型微分方程為[19]:
(3)
式中,b為常數;F=y(t)/m,它是t時刻市場汽車保有量y(t)與市場最大保有量m的比值。
由分離變量法求解式(3)得:
(4)
式中,a為常數。最終得t時刻汽車保有量為:
y(t)=m×F(t)。
(5)
1.3 改進PCA-Logistic模型
結合前面兩個方法,提出改進PCA-Logistic模型。首先選取影響我國個人汽車保有量的幾個代表性因素作為評價指標,將原始數據進行對數轉換,以消除非線性的影響,再進行標準化處理以消除量綱或數量級上的差異。然后再利用SPSS軟件中的降維因子分析模塊對其進行改進的主成分分析,確定主成分,并計算主成分得分。
根據主成分貢獻率及累計貢獻率的計算結果,選擇第一主成分FAC1_1作為自變量,個人汽車保有量作為因變量,對其進行Logistic模型回歸分析,由于沒有采用時間序號作為自變量,對公式(4)進行等價變換,最終采取的模型方程為:
(6)
式中,α0和α1為待求參數。采用非線性最小二乘法進行參數求解,首先選取合適的最大個人汽車保有量m作為固定值,然后給出參數α0和α1初始值進行迭代求解,迭代算法為麥夸特法。
2 實證分析
2.1 變量選取與數據來源
通過文獻資料的搜集與整理可以發現[20],影響我國個人汽車保有量變化的因素有多種,如經濟因素,包括人均GDP、居民收入、經濟產業結構、居民消費水平等;社會因素,包括城市人口、城市化率、失業率、擁塞成本等;環境因素,包括公路網規模、基礎設施完善度等。考慮長期完整數據的可獲得性,選取了城市人口、城市化水平、人均GDP、居民消費水平、公路里程、第一產業生產值所占比重、第二產業生產值所占比重、第三產業生產值所占比重這8個代表性的影響因素進行分析。我國個人汽車保有量及其影響因素的樣本數據見表1,選取區間為1985—2018年,統計數據均來源于《中國統計年鑒》[2-5]。
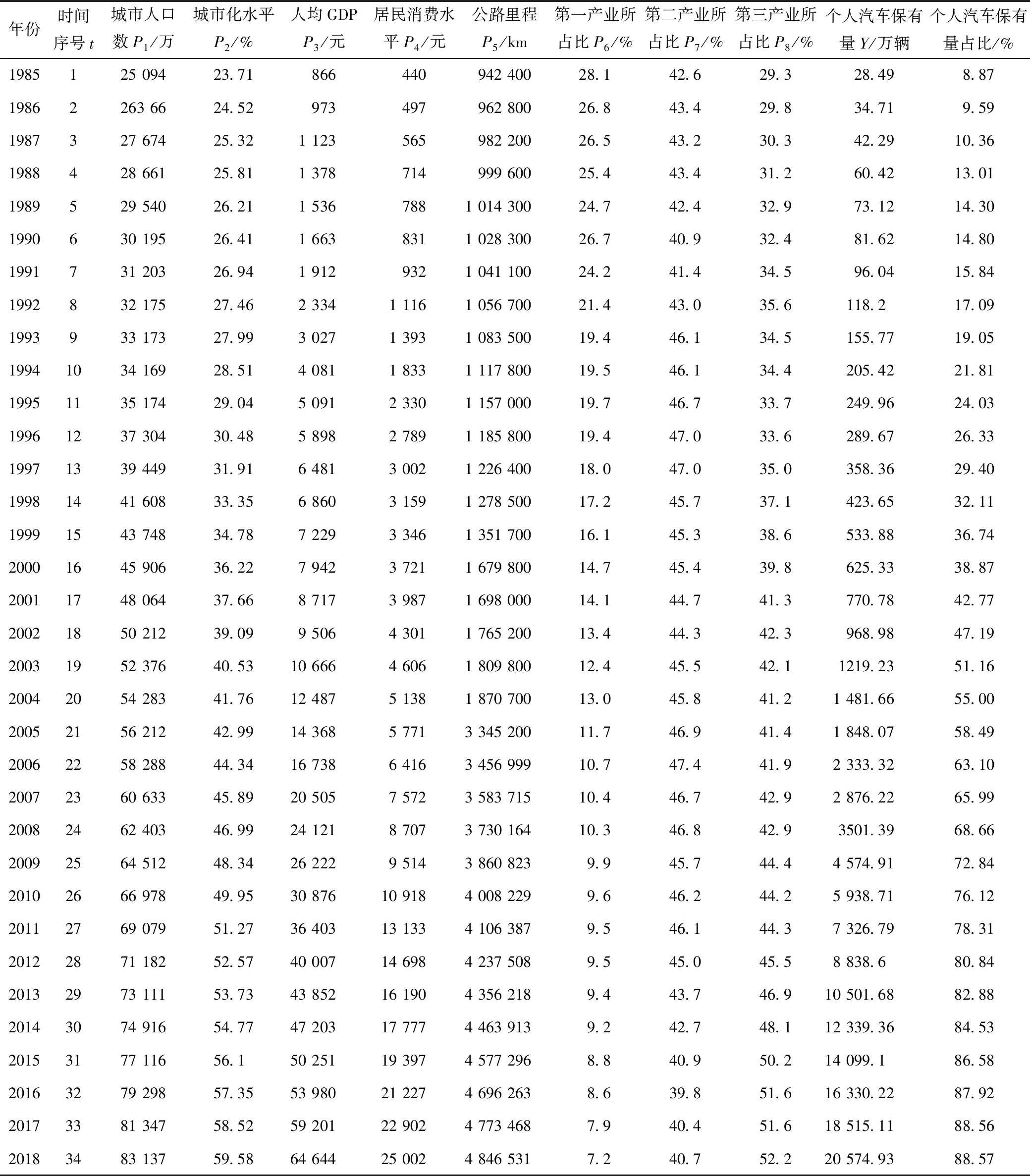
表1 我國個人汽車保有量與影響指標因素數據(1985—2018)Tab.1 Data of private car ownership in China and influencing factors(1985—2018)
2.2 改進的主成分分析
應用SPSS22.0計算軟件,對我國個人汽車保有量的影響因素按以下步驟提取主成分:
(1)將原始數據進行對數變換處理。
(2)將變換后的8個影響因素標準化處理后,再進行主成分分析,得到解釋的總方差見表2。
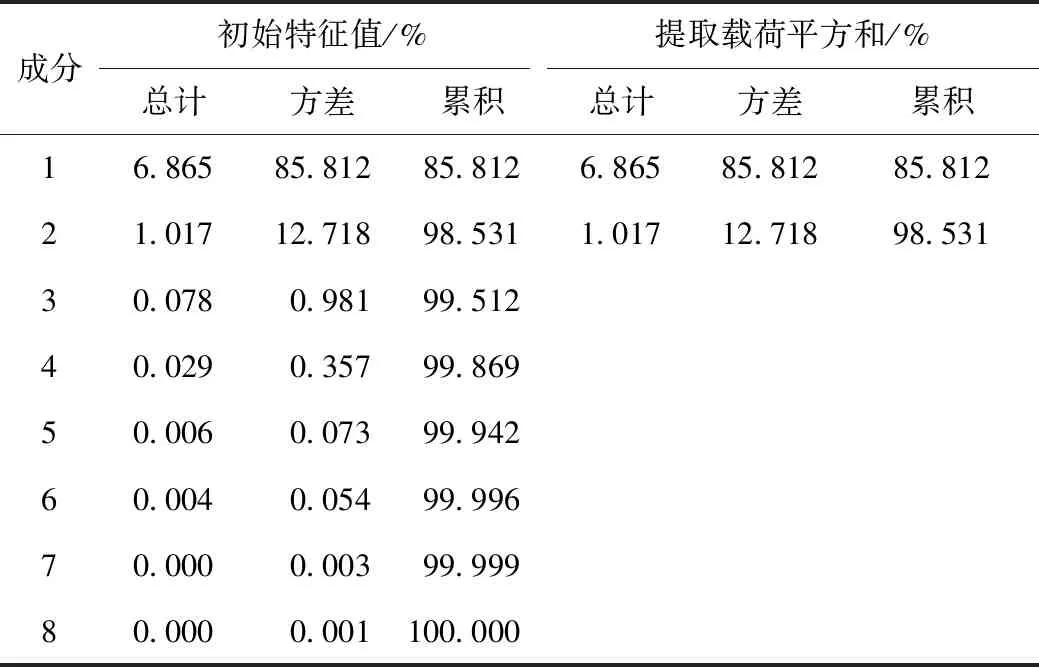
表2 總方差解釋Tab.2 Explanation of total variance
由表2可以看到,第一主成分的特征值為6.865,其方差占總方差比為85.812%,對個人汽車保有量影響占主要作用,根據主成分選擇標準,將原來的8個影響因素用這一個主成分來代替。
(3)成分得分系數矩陣見表3。根據表3可以寫出第一主成分的因子表達式為:
Y1=0.146P1+0.145P2+0.145P3+0.144P4+
0.142P5-0.145P6-0.008P7+0.143P8。
(7)
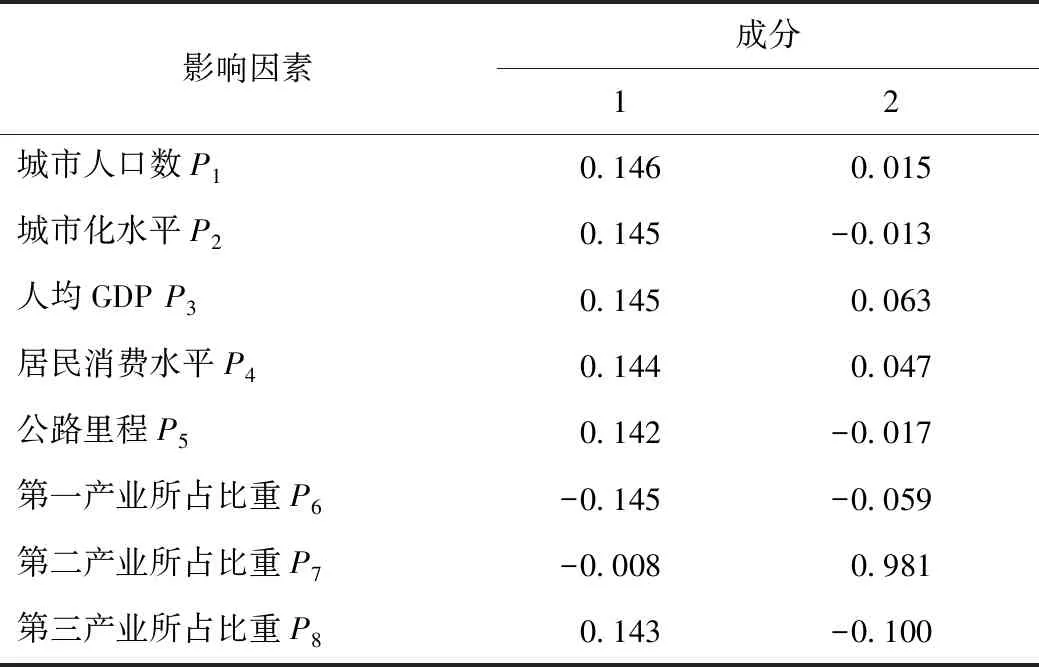
表3 成分得分系數矩陣Tab.3 Component score coefficient matrix
根據上述表達式對標準化后的數據進行計算,計算后的第一主成分FAC1_1相關數據見表4。
2.3 主成分分析法改進前后的主成分回歸曲線比較
利用1985-2018年之間我國個人汽車保有量的影響因素原始數據,采用傳統主成分分析法進行分析。圖1與圖2分別表示用傳統主成分分析法與改進主成分分析法擬合得到的第一主成分FAC1_1與時間序號的回歸曲線,從兩個圖可以看出傳統主成分分析法的回歸曲線與時間幾乎呈現二次非線性關系,而改進主成分分析法得到的回歸曲線和時間幾乎呈現線性關系。由于主成分分析方法更適用于線性結構數據,可以看出通過改進主成分分析法消除了數據之間的非線性關系,更符合主成分分析法的原則,從而有利于提高預測的準確性。
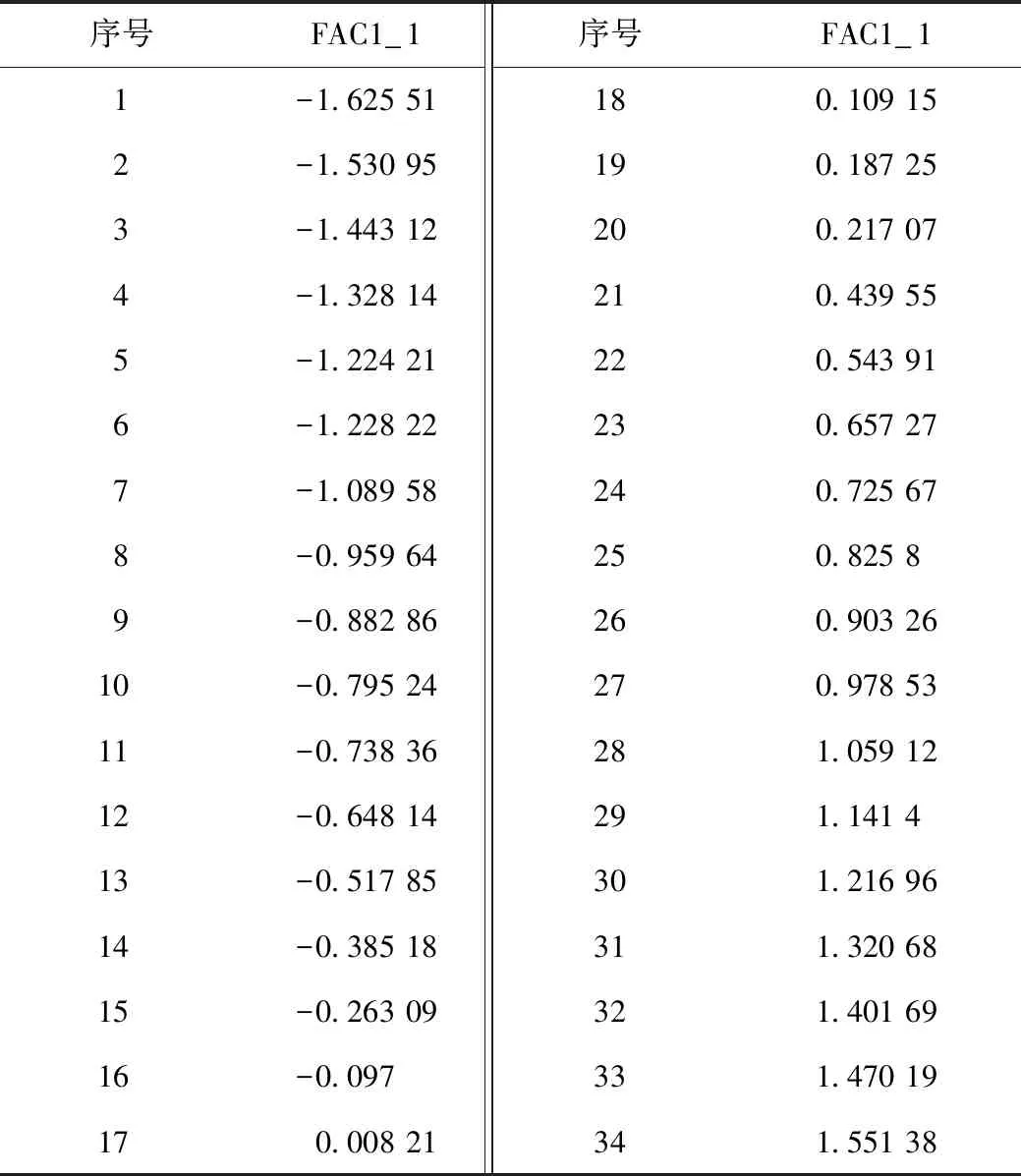
表4 第一主成分FAC1_1計算數據Tab.4 Calculated data of 1st principal component FAC1_1
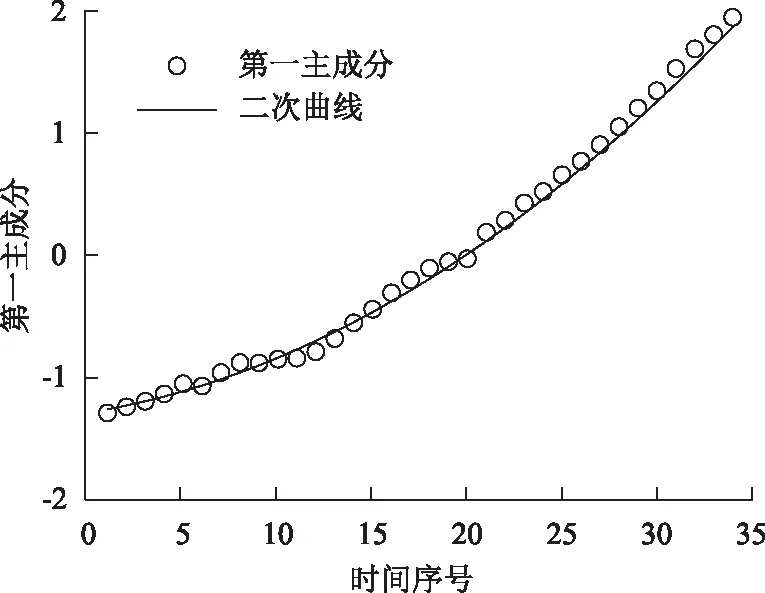
圖1 傳統主成分分析法的第一主成分FAC1_1與 時間序號的回歸曲線Fig.1 Regression curve of 1st principal component FAC1_1 vs. time serial number by conventional PCA
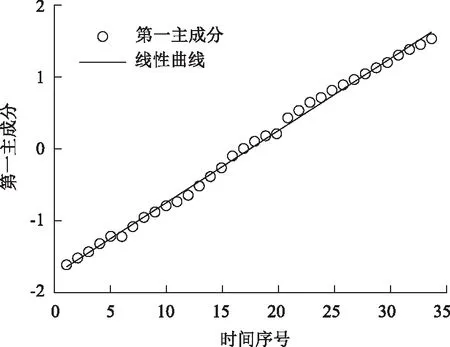
圖2 改進主成分分析法的第一主成分FAC1_1與 時間序號的回歸曲線Fig.2 Regression curve of 1st principal component FAC1_1 vs. time serial number by improved PCA
利用線性回歸模型可得改進主成分分析法的第一主成分FAC1_1與時間序號t之間的回歸公式為:
FAC1_1=-1.754+0.1t。
(8)
2.4Logistic模型回歸分析2.4.1改進主成分分析法的Logistic回歸分析
利用Logistic模型對第一主成分FAC1_1和個人汽車保有量進行回歸分析,由于最大汽車保有量m具有不確定性,需要提前進行估算。對m的估算方法大致有3種,分別是直接選取最大值法、專家判斷法和純粹數學推導法。本研究采用專家判斷法確定個人汽車最大保有量m。根據文獻[21],國家信息中心信息資源部主任徐長明認為,汽車保有量最高可達4.5億輛。根據表1中個人汽車保有量占比的歷年數據,可以看出該比值一直呈增長趨勢,1985年為8.87%,2018年為88.57%,為了合理地預估我國個人汽車保有量極限,本研究假設其極限占比為90%,計算得出我國個人汽車最大保有量為4.05億輛,則原公式(6)變為:
(9)
令α0和α1的初始值為1,利用計算工具SPSS22.0對樣本數據進行Logistic非線性回歸,得到的參數估計結果見表5。

表5 改進PCA-Logistic模型的參數估計結果Tab. 5 Estimated parameters by improved PCA-Logistic model
根據表5可得到擬合程度的相關系數為R2=0.998。當R2越接近于1,表明回歸曲線與數據越接近,可以看出得到的Logistic回歸曲線擬合程度非常高,最后曲線方程為:
(10)
2.4.2主成分分析法改進前后的Logistic回歸比較
同樣根據上述步驟,利用傳統PCA-Logistic模型對我國個人汽車保有量進行回歸分析,得到的參數估計結果見表6,此時R2=0.996<0.998,說明改進PCA-Logistic模型的回歸曲線擬合程度更好,會使預測結果更準確。
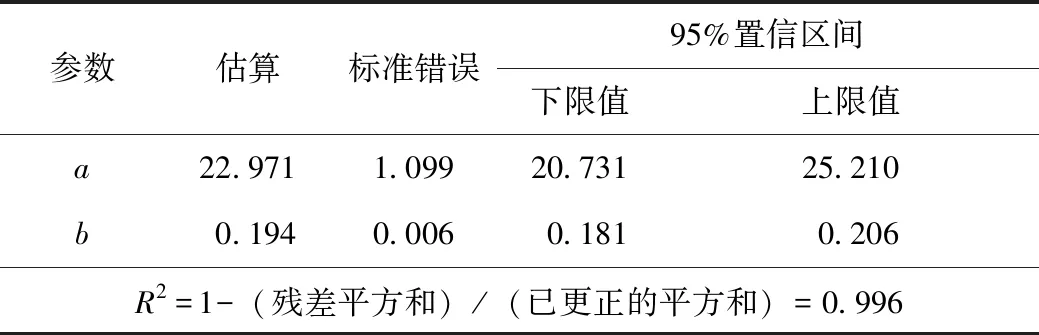
表6 傳統PCA-Logistic模型的參數估計結果Tab.6 Estimated parameters by conventional PCA-Logistic model
圖3是主成分分析法改進前后通過Logistic模型得到的個人汽車保有量預測曲線與實際汽車保有量數據點的比較,橫坐標為時間序號。由圖可以看出,在2007年之前,傳統PCA-Logistic模型得到的個人汽車保有量預測數據曲線要高于實際個人汽車保有量數據點,而在2007年之后,其又低于實際個人汽車保有量數據點。而改進PCA-Logistic得到的個人汽車保有量數據曲線更接近實際個人汽車保有量數據點,這也再次證明改進主成分分析法有利于提升Logistic回歸曲線的擬合度,并提高預測的準確度。

圖3 主成分分析法改進前后Logistic模型的預測值 與實際值對比Fig.3 Comparison of predicted and actual values obtained by Logistic model before and after PCA improvement
2.5 個人汽車保有量預測
為了預測我國2019—2024年的個人汽車保有量,將對應時間序號代入公式(8)中得相應的FAC1_1值,再將所得結果代入Logistic模型公式(10),可得2019—2024年個人汽車保有量預測值見表7。

表7 2019—2024年個人汽車保有量預測值Tab.7 Predicted values of private car ownership from 2020 to 2024
經過預測,我國個人汽車保有量在2021年可能會突破3億。2019年實際個人汽車保有量為22 635萬輛,發現預測值大于實際值,這可能是因為近來年國家為了緩解交通擁擠壓力而實施的限購限號等政策延緩了汽車保有量的高速增長,說明國家政策會短期性的影響個人汽車保有量的變化。
3 結論
通過對數變換法對傳統主成分分析法進行了改進,并結合Logistic模型,提出了改進PCA-Logistic模型。采用改進主成分分析法對影響我國個人汽車保有量的8個代表性主要因素進行“非線性”降維處理并提取主成分,利用Logistic回歸模型研究主成分與汽車保有量之間的關系。
通過將PCA-Logistic模型改進前后得到的估計結果進行對比,發現改進PCA-Logistic模型可以有效地消除長時間跨度的數據之間的非線性關系,得到的線性主成分回歸曲線更符合主成分分析法原則,同時也有效地提高Logistic模型回歸的擬合度,從而更準確地預測未來我國個人汽車保有量。經過預測,我國個人汽車保有量在2021年可能會突破3億。
本研究在提取主成分時僅僅對影響因素進行分析,沒有考慮其與汽車保有量之間的關系,也沒有考慮國家政策對汽車保有量的影響,后續工作會考慮更多的影響因素進行分析,從而對汽車保有量進行更合理的評價。

