圖的奇優美性與奇強協調性
林育青,鐘發勝,曹 蓉,童細心
(汕頭職業技術學院自然科學系,廣東 汕頭 515041)
0 引言
優美圖的提出始于1963年G.Ringel[1]的一個猜想和1967 A.Rosa[2]的一篇論文.1972年,S.W.Golomb[3]明確給出了優美圖的定義.1982年,Fank Hsu D[4]引入圖的強協調標號;1994年,Gnanajoethi提出另一個猜想:“每棵樹都是奇優美的”[5-6],又推動了對圖的奇優美性和奇強協調性的研究,也取得了一些成果[7-18].但由于缺乏一個系統和有力的工具,迄今,只能對一些特殊圖探索其奇優美性和奇強協調性.本文給出了圖的定義,討論了圖的奇優美性與奇強協調性并給出了標號算法.
定義 1[5]對于簡單圖 G=(V,E),如果存在一個映射滿足:1)f是單射;2)有:
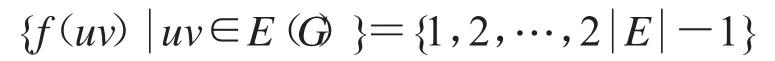
則稱圖G是奇優美圖,f稱為G的奇優美標號.
定義 2[4]對于簡單圖 G=(V,E),如果存在一個映射滿足:1)f是單射;2),令f(uv)=f(u)+f(v)有:
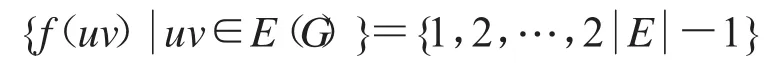
則稱圖G是奇強協調的,f稱為G的奇強協調標號.
定義3[7]在含有n個頂點的路Pn上,當且僅當兩點的距離為m(m≥2)時增加一條邊,這樣所得到的圖稱為.
定義4在含有n個頂點的路Pn上,當且僅當兩點的距離為m(m≥2)時增加一條長度為2的邊,這樣所得到的圖稱為的細分圖,記為.

圖 1 圖
本文所討論的圖均為無向簡單圖,其它未加說明的定義和符號均來自文獻[19].
1 主要結果及證明
下面分兩種情形證明.
(1)v2i-1=vi,i,i=1,2,…,k;
(2)v2i=vi+1,i,i=1,2,…,k;
(3)v2i-1,2i+1=vi,i+1,i=1,2,…,k-1;
(4)v2i,2i+2=vi+1,i-1,i=1,2,…,k-1.

圖 2 圖P(2k,2)的頂點標記
下面給出P(2k,2)的頂點標號算法A:
算法A(1)f(vi,i+1)=(12k-7)-6i,i=1,2,…,k-1;
(2)f(vi,i)=6i-6,i=1,2,…,k
(3)f(vi+1,i)=(12k-5)-6i,i=1,2,…,k
(4)f(vi+2,i)=6i-2,i=1,2,…,k-1
下面驗證算法A是圖P(2k,2)的一個奇優美標號算法,從而也是圖的一個奇優美標號算法.


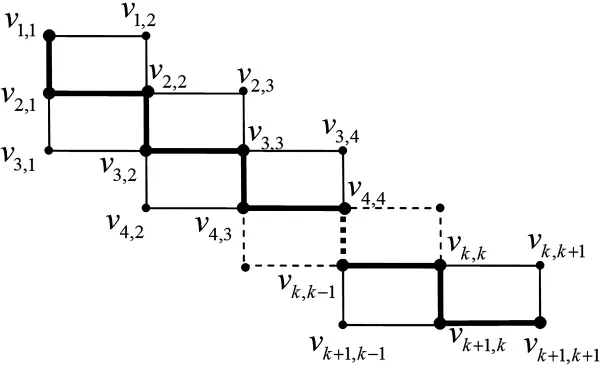
圖 3 圖 P(2k+1,2)的頂點標記





綜上,由引理2.3、2.4及定義2,當n=2k+1時,圖是奇強協調圖,即情形4成立.
2 實例
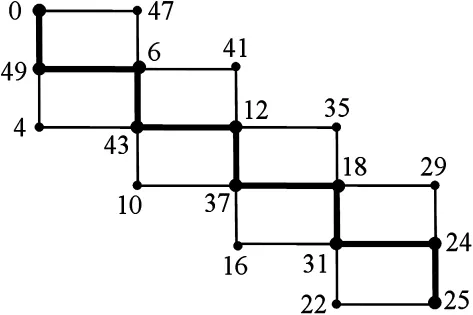
圖4 圖的奇優美標號
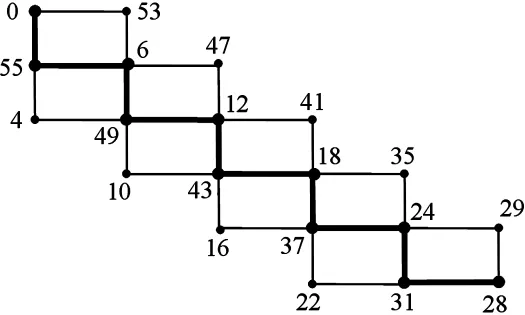
圖 5 圖的奇優美標號
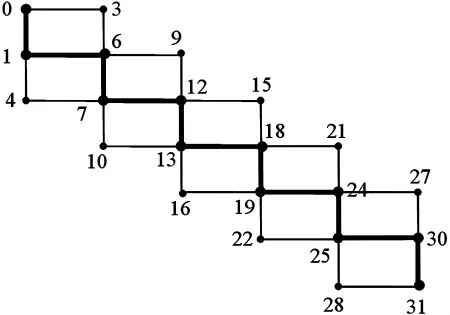
圖6 圖的奇強協調標號
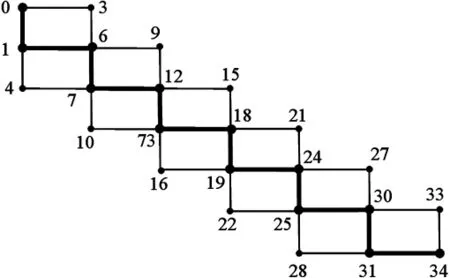
圖 7 圖的奇強協調標號

